2021-2022学年江苏省各地苏科版数学七年级上册2.8有理数的混合运算期末试题分类选编(Word版含答案)
文档属性
| 名称 | 2021-2022学年江苏省各地苏科版数学七年级上册2.8有理数的混合运算期末试题分类选编(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 570.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览




文档简介
2.8 有理数的混合运算
1.(2022·江苏宿迁·七年级期末)如果规定符号“”的意义为,则的值是( )
A.5 B.-5 C.1 D.
2.(2022·江苏宿迁·七年级期末)取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明,但举例验证都是正确的.例如:取自然数5,经过下面5步运算可得1,即:如图所示.如果自然数m恰好经过7步运算可得到1,则所有符合条件的m的值有( )
A.6个 B.5个
C.4个 D.3个
3.(2022·江苏淮安·七年级期末)新华书店开业期间推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元但不超过200元一律打九折;③一次性购书200元律打八折.如李明明同学一次性购书付款162元,那么李明明所购书的原价一定为( )
A.180元 B.200 元
C.200元或202.5元 D.180元或202.5元
4.(2022·江苏扬州·七年级期末)如图,在这个数运算程序中,若开始输入的正整数n为奇数,都计算3n+1;若n为偶数,都除以2.若n=21时,经过1次上述运算输出的数是64;经过2次上述运算输出的数是32;经过3次上述运算输出的数是16;…;经过2022次上述运算输出的数是( ).
A.1 B.2 C.3 D.4
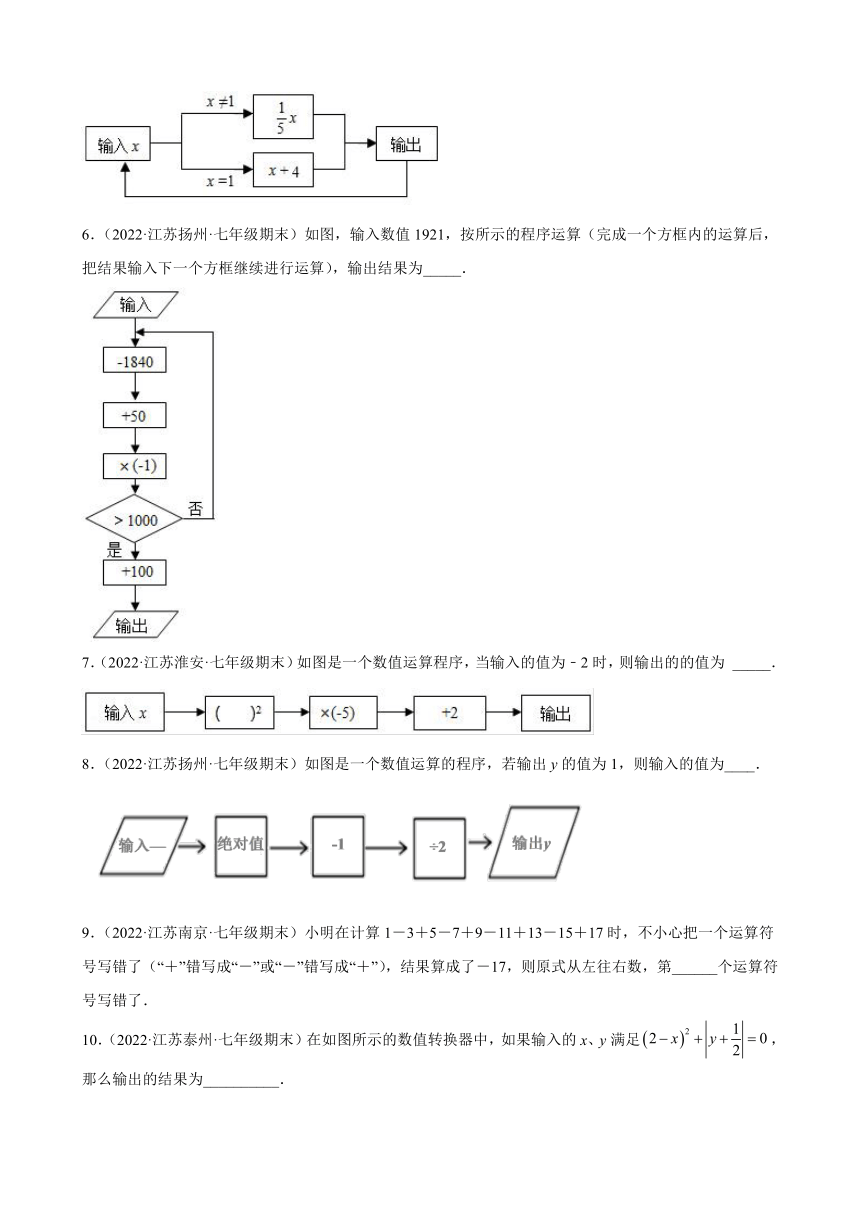
5.(2022·江苏宿迁·七年级期末)如图,是一个运算程序的示意图,若开始输入x的值为25,则第2022次输出的结果为_____.
6.(2022·江苏扬州·七年级期末)如图,输入数值1921,按所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),输出结果为_____.
7.(2022·江苏淮安·七年级期末)如图是一个数值运算程序,当输入的值为﹣2时,则输出的的值为 _____.
8.(2022·江苏扬州·七年级期末)如图是一个数值运算的程序,若输出y的值为1,则输入的值为____.
9.(2022·江苏南京·七年级期末)小明在计算1-3+5-7+9-11+13-15+17时,不小心把一个运算符号写错了(“+”错写成“-”或“-”错写成“+”),结果算成了-17,则原式从左往右数,第______个运算符号写错了.
10.(2022·江苏泰州·七年级期末)在如图所示的数值转换器中,如果输入的x、y满足,那么输出的结果为__________.
11.(2022·江苏无锡·七年级期末)我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为_____个.
12.(2022·江苏淮安·七年级期末)计算:
(1)2×(﹣2)+3
(2)
13.(2022·江苏泰州·七年级期末)计算:
(1);
(2).
14.(2022·江苏盐城·七年级期末)计算:
(1)
(2)
15.(2022·江苏无锡·七年级期末)计算:
(1);
(2)
16.(2022·江苏·苏州市振华中学校七年级期末)计算:
(1)
(2)
17.(2022·江苏淮安·七年级期末)计算:
(1);
(2)
18.(2022·江苏扬州·七年级期末)计算:
(1);
(2)
19.(2022·江苏南通·七年级期末)气象资料表明,高度每增加1000m,气温大约下降6℃.
(1)某山峰高1700m,当山脚的温度为时,求山顶气温;
(2)为估算某山峰的高度,两名研究人员同时在上午10点测得山脚和山顶的气温分别为9℃和-3℃,请估算此山峰的高度是多少米?
20.(2022·江苏扬州·七年级期末)某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中五次行驶记录如下(单位:千米):
第一次 第二次 第三次 第四次 第五次
﹣3 8 ﹣9 +10 ﹣2
(1)在第 次记录时距A地最远;
(2)收工时距A地 千米;
(3)若每千米耗油0.4升,每升汽油需6.5元,问检修小组工作一天需汽油费多少元?
21.(2022·江苏常州·七年级期末)(1)
(2)
22.(2022·江苏南京·七年级期末)计算:(1);
(2)
23.(2022·江苏南京·七年级期末)计算:
(1);
(2).
24.(2022·江苏南通·七年级期末)计算:
(1);
(2).
25.(2022·江苏·射阳县第六中学七年级期末)计算:
(1);
(2).
26.(2022·江苏常州·七年级期末)计算:
(1);
(2).
27.(2022·江苏苏州·七年级期末)计算:.
28.(2022·江苏无锡·七年级期末)计算:
(1)5×(﹣)﹣|﹣6|+(﹣3);
(2).
29.(2022·江苏·南京市第二十九中学七年级期末)计算:
(1)-14-[4-(-3)2] (2)(- +)×(-24)
30.(2022·江苏南京·七年级期末)计算:
(1);
(2).
31.(2022·江苏南通·七年级期末)计算:
(1);
(2).
32.(2022·江苏无锡·七年级期末)计算下列各题:
(1)23﹣(﹣7)+(﹣6);
(2).
33.(2022·江苏扬州·七年级期末)计算:
(1)
(2)
34.(2022·江苏南通·七年级期末)计算:
(1)﹣20+(+3)﹣(﹣5)﹣(+7);
(2)﹣2.5×(﹣);
(3)2×(﹣3)3﹣4×(﹣3)+15;
(4)(﹣2)3+(﹣3)×[(﹣4)3+2]﹣(﹣3)2÷(﹣2).
35.(2022·江苏宿迁·七年级期末)计算:
36.(2022·江苏江苏·七年级期末)计算:
(1);
(2).
37.(2022·江苏无锡·七年级期末)计算:
(1)12﹣(﹣18)+(﹣7)﹣15;
(2)(﹣1)2×(﹣23)﹣(﹣4)÷2×.
38.(2022·江苏·射阳县第六中学七年级期末)计算:
(1);
(2).
39.(2022·江苏·无锡市东林中学七年级期末)计算:
(1);
(2)
40.(2022·江苏扬州·七年级期末)计算:
(1)
(2)
41.(2022·江苏南京·七年级期末)计算:
(1)×(-18);
(2)-24-(-2)3÷×(-3)2.
42.(2022·江苏无锡·七年级期末)计算:
(1);
(2).
43.(2022·江苏南京·七年级期末)计算:
(1)-12-2+(-3)×;
(2).
44.(2022·江苏南京·七年级期末)计算:
(1);
(2).
45.(2022·江苏苏州·七年级期末)计算:
(1);
(2).
46.(2022·江苏徐州·七年级期末)计算:
(1)3+(-4)+6-(-2);
(2)2×(-3)2-5÷
47.(2022·江苏苏州·七年级期末)计算:
(1);
(2).
48.(2022·江苏泰州·七年级期末)计算
(1)
(2)
49.(2022·江苏南通·七年级期末)计算:
(1);
(2).
参考答案:
1.B
【解析】根据新定义代入,即可求解.
解:根据题意得:.
故选:B
本题主要考查了有理数的混合运算,理解新定义是解题的关键.
2.C
【解析】首先根据题意,应用逆推法,用1乘以2,得到2;用2乘以2,得到4;用4乘以2,得到8;用8乘以2,得到16;然后分类讨论,判断出所有符合条件的m的值为多少即可.
定义新运算
故答案为C
本题考查逆推法,熟练掌握计算法则是解题关键.
3.D
【解析】不享受优惠即原价,打九折即原价×0.9,打八折即原价×0.8.
解:∵200×0.9=180,200×0.8=160,160<162<180,
∴一次性购书付款162元,可能有两种情况.
162÷0.9=180元;162÷0.8=202.5元.
故王明所购书的原价一定为180元或202.5元.
故选:D.
本题考查有理数的运算在实际生活中的应用.注意售书有三种优惠方案.
4.B
【解析】分别求出部分输出结果,发现第1次输出结果到第4次输出结果只出现一次,从第5次输出结果开始,每3次结果循环一次,则经过2022次上述运算输出的数与第6次输出的结果相同,由此可求解.
解:当n=21时,
经过1次运算输出的数是64,
经过2次运算输出的数是32,
经过3次运算输出的数是16,
经过4次运算输出的数是8,
经过5次运算输出的数是4,
经过6次运算输出的数是2,
经过7次运算输出的数是1,
经过8次运算输出的数是4,
经过9次运算输出的数是2,
……
∴第1次输出结果到第4次输出结果只出现一次,从第5次输出结果开始,每3次结果循环一次,
∵(2022﹣4)÷3=672……2,
∴经过2022次上述运算输出的数与第6次输出的结果相同,
故选:B.
本题考查数字的变化规律,通过运算找到输出结果的循环规律是解题的关键.
5.1
【解析】由题意利用程序图进行运算,可以发现从第一次开始输出的结果以5,1为循环节循环,由此可得结论.
解:由题意得:
第一次输入25,输出结果为:5;
第二次输入5,输出结果为:1;
第三次输入1,输出结果为:5;
第四次输入5,输出结果为:1;
第五次输入1,输出结果为:5;
第六次输入5,输出结果为:1;
∴从第一次开始输出的结果以5,1为循环节循环,
∵2022÷2=1011,
∴第2022次输出的结果为:1.
故答案为:1.
本题主要考查了求代数式的值,有理数的混合运算,本题是操作型题目,理解并正确操作程序是解题的关键.
6.2021
【解析】把1921代入程序中计算,判断即可得到结果.
解:把1921代入得:(1921-1840+50)×(-1)=-131<1000,
把-131代入得:(-131-1840+50)×(-1)=1921>1000,
则输出结果为1921+100=2021.
故答案为:2021.
本题考查了有理数的混合运算,弄清程序中的运算过程是解本题的关键.
7.-18
【解析】把x=﹣2代入运算程序求值即可得最后结果.
解:把x=﹣2代入得,
(﹣2)2×(﹣5)+2
=4×(﹣5)+2
=﹣20+2
=﹣18,
故答案为:﹣18.
本题考查了代数式求值,有理数的混合运算,掌握运算程序的意义,读懂题意是解题关键.
8.
【解析】设输入的数为x,根据程序列出关于x的方程,求出x即可.
设输入的数为x,根据程序列方程得
÷2=1
故答案为
本题考查了整式的程序计算,正确理解程序是解题的关键.
9.6
【解析】先确定哪一个数的符号出了错,再确定这个符号是第几个.
∵1-3+5-7+9-11+13-15+17=9,
∴-17小于9,
∴一定是把+错写成减号了,
∴这个数为[9-(-17)]÷2=13,
∴是第六个符号写错了,
故答案为:6.
本题考查了有理数的混合运算,大小的比较,熟练进行计算是解题的关键.
10.0.5##
【解析】根据(2 x)2+|y+|=0,可以得到x、y的值,然后将x的值代入,求出最后可以输出的x的值即可.
解:∵,
∴2-x=0,y+=0,
解得x=2,y=-,
∴(-0.5)x=(-0.5)×2=-1<-,
当x=-1时,(-0.5)x=(-0.5)×(-1)=0.5>-,
故答案为:0.5.
本题考查有理数的混合运算、非负数的性质,解答本题的关键是求出最后的x的值.
11.1838
分析:类比于现在我们的十进制“满十进一”,可以表示满六进一的数为:万位上的数×64+千位上的数×63+百位上的数×62+十位上的数×6+个位上的数,即1×64+2×63+3×62+0×6+2=1838.
详解:2+0×6+3×6×6+2×6×6×6+1×6×6×6×6=1838,
故答案为1838.
点睛:本题是以古代“结绳计数”为背景,按满六进一计数,运用了类比的方法,根据图中的数学列式计算;本题题型新颖,一方面让学生了解了古代的数学知识,另一方面也考查了学生的思维能力.
12.(1)-1 ;
(2)7
【解析】(1)
解:2×(﹣2)+3
=-4+3
=-1
(2)
解:
此题主要考查了有理数的混合运算,熟悉运算法则是解题关键.
13.(1)
(2)4
【解析】(1)
解:
(2)
解:
本题考查了有理数的混合运算,解题的关键是掌握运算法则和运算顺序.
14.(1)15
(2)0
【解析】(1)先去括号去绝对值符号,再根据运算顺序,先算乘除再算加减;
(2)先去括号,根据运算顺序,先算乘方再算乘除再算加减;
(1)
解:原式=8-5+43
=8-5+12
=15
(2)
解:原式=-1+
=-1+1
=0
本题考查了有理数的混合运算,解题的关键是熟练掌握绝对值、乘方以及乘法的分配律,有理数相乘的时候可以根据同号正异号负的原则先确定符号再运算绝对值.
15.(1)-8
(2)5
【解析】(1)先计算乘法,再计算加减法;
(2)先计算乘方及乘法,再计算除法,最后计算加减法.
(1)
解:原式
.
(2)
解:原式
=-1+6
.
此题考查了有理数的混合运算及含乘方的有理数的混合运算,正确掌握运算顺序及运算法则是解题的关键.
16.(1)
(2)
【解析】(1)先算乘方,再算乘法,最后算减法;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;
(2)先算乘除,后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;注意乘法分配律的运用.
(1)
解:
=
=
=
=
(2)
解:
=
=
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
17.(1)
(2)
【解析】(1)
解:
(2)
解:
本题考查的是含乘方的有理数的混合运算,掌握“有理数的混合运算的运算顺序”是解本题的关键,有理数的混合运算的运算顺序:先乘方,再乘除,最后算加减,有括号先算括号内的运算.
18.(1)18
(2)
【解析】(1)
(2)
本题考查了有理数的混合运算,掌握有理数的混合运算是解题的关键.
19.(1)7.8℃
(2)2000米
【解析】(1)由减去降低的温度即可;
(2)先计算出山脚与山顶的温差,再除以6,再乘以1000即可得到答案.
(1)解:℃.答:山顶气温7.8℃.
(2)解:m.答:此山峰的高度是2000m.
本题考查的是有理数的四则混合运算的实际应用,理解题意列出正确的运算式是解本题的关键.
20.(1)4
(2)4
(3)83.2
【解析】(1)五次行驶的和即收工时检修小组距离A地的距离;
(2)计算每一次记录检修小组离开A的距离,比较后得出检修小组距A地最远的次数;
(3)每次记录的绝对值的和,是检修小组一天的行程,根据单位行程的耗油量计算出该检修小组一天的耗油量.
(1)
第一次后,检修小组距A地3km;
第二次后,检修小组距A地 3+8=5(km);
第三次后,检修小组距A地 3+8 9= 4(km)
第四次后,检修小组距A地 3+8 9+10=6(km)
第五次后,检修小组距A地 3+8 9+10-2=4(km)
故在第四次记录时距A地最远
故答案为:4
(2)
3+8 9+10 2=4(km),
所以收工时距A地4 km
故答案为4;
(3)
(3+8+9+10+2)×0.4×6.5=83.2(元)
答:检修小组工作一天需汽油费83.2元.
本题考查了有理数的加减法在生活中的应用.解题的关键是熟知耗油量=行程×单位行程耗油量.
21.(1)26;(2)
解:(1)
;
(2)
,
,
,
;
本题考查了含乘方的有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
22.(1)40;(2)-4
【解析】(1)先算乘方,再算乘法,最后算加法;
(2)先算乘方,再算除法,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有绝对值,要先做绝对值内的运算.
解:(1)原式=4+36
=40;
(2)原式=-1+6-9
=-4.
考查了有理数混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
23.(1)27;(2)-11;
【解析】(1)先利用乘法分配律并去括号,在进行加减运算;
(2)先算括号里面的,再算括号外面的算式,括号内先算乘法再算加减.
(1)解:原式
.
(2)解:原式
.
有理数的混合运算,应注意运算顺序,先乘方,再乘除,再加减,有括号先算括号.
24.(1)8
(2)
【解析】(1)去括号后再计算即可;
(2)先乘方,再乘除,最后加减,计算即可.
(1)
解:
∴原式的值为.
(2)
解:
∴原式的值为.
本题考查了整式的加减,分数的混合运算,同分母分数加减,有理数的乘方等知识.解题的关键在于正确的去括号与乘除运算.
25.(1)-5
(2)15
【解析】(1)利用乘法分配律展开计算即可;
(2)先算乘方,和绝对值,再算除法,最后算加减.
(1)
解:
=
=
=
(2)
=
=
=
本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
26.(1);
(2).
【解析】(1)先计算乘法,再加减即可;
(2)先计算绝对值,乘方,再计算加减即可.
(1)
解:,
=,
=;
(2)
解:,
=,
=.
本题考查含乘方的有理数混合运算,掌握含乘方的有理数混合运算法则,先乘方,再乘除,最后加减,有括号先小括号,中括号再大括号是解题关键.
27.9
【解析】先算括号,再计算乘方,然后计算乘除,最后计算加减.
解:
.
本题考查含乘方的有理数的混合运算,是重要考点,掌握相关知识是解题关键.
28.(1)-11;
(2)-3.
【解析】(1)先算乘法,后算加减;同级运算,应按从左到右的顺序进行计算;如果有绝对值,要先做绝对值内的运算;
(2)先算乘方,再算除法,最后算加法;同级运算,应按从左到右的顺序进行计算.
(1)
解:5×(-)-|-6|+(-3)
=-2-6-3
=-11;
(2)
解:( 1)2002÷+42+( 3)3
=1÷+16-27
=1×8+16-27
=8+16-27
=-3.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
29.(1)4;(2)-22
【解析】(1)先计算乘方,再计算加减法;
(2)根据乘法分配律计算.
解:(1)-14-[4-(-3)2]
=-1-(-5)
=4;
(2)(- +)×(-24)
=×(-24)-×(-24)+×(-24)
=-6+20-36
=-22.
此题考查了有理数的计算,正确掌握含乘方的有理数的混合运算法则、乘法分配律法则是解题的关键.
30.(1)
(2)
【解析】(1)
解:
(2)
解:
.
本题主要考查了有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
31.(1)-3.8
(2)
【解析】(1)
解:原式;
(2)
解:原式.
本题主要考查了有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
32.(1)24
(2)﹣6
【解析】(1)根据有理数的加减运算法则进行计算即可;
(2)先算乘方,再算括号内运算,再算乘法,最后算减法即可.
(1)解:23﹣(﹣7)+(﹣6)=23+7﹣6=30﹣6=24
(2)解:
本题考查有理数的混合运算,要熟练掌握运算法则,注意运算顺序.
33.(1)-3
(2)1
【解析】(1)
解:
(2)
解:
本题考查的是含乘方的有理数的混合运算,有理数乘法的分配律的应用,掌握“有理数的混合运算的运算顺序”是解本题的关键,有理数的混合运算的运算顺序为:先乘方,再乘除,最后算加减,有括号先计算括号内的运算.
34.(1)-19;
(2)1;
(3)-27;
(4)182.5.
【解析】(1)
解:﹣20+(+3)﹣(﹣5)﹣(+7)
=-20+3+5-7
=-19;
(2)
解:﹣2.5×(﹣)
=-××(-)
=1;
(3)
解:2×(﹣3)3﹣4×(﹣3)+15
=2×(-27)+12+15
=-54+12+15
=-27;
(4)
解:(﹣2)3+(﹣3)×[(﹣4)3+2]﹣(﹣3)2÷(﹣2)
=-8+(﹣3)×(﹣64+2)-9÷(﹣2)
=-8+(﹣3)×(﹣62)+9÷2
=-8+186+4.5
=182.5.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
35.23
【解析】先计算乘方、绝对值,然后计算乘除,最后计算加减,即可得到答案.
解:
本题考查了有理数的混合运算.解题的关键在于明确先计算乘方、绝对值,然后计算乘除,最后计算加减.
36.(1)
(2)0
【解析】(1)先把除法转化为乘法,再利用乘法的运算法则求解即可;
(2)先算乘方,再进行括号里的运算,接着算乘法,最后算加法即可.
(1)
解:
=(﹣12)×(﹣)×
=;
(2)
解:
=﹣1﹣×(5﹣9)
=﹣1﹣×(﹣4)
=﹣1+1
=0.
本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.
37.(1)8;
(2)-7.
【解析】(1)
解:12﹣(﹣18)+(﹣7)﹣15
=12+18-7-15
=8;
(2)
解:(﹣1)2×(﹣23)﹣(﹣4)÷2×
=1×(﹣8)+4××
=-8+1
=-7.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
38.(1)
(2)
【解析】(1)
(2)
本题考查了有理数的混合运算,正确的计算是解题的关键.
39.(1)-12;
(2)18
【解析】(1)
解:
=-12;
(2)
解:
=18.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
40.(1)-6 ;(2)15
【解析】(1)利用减法法则变形,进行计算即可求解;
(2)先计算乘方,再利用有理数的乘方运算律计算乘法,最后计算加减,即可求解.
解:(1)
;
(2)
.
本题主要考查了有理数的混合运算,熟练掌握相关运算法则是解题的关键.
41.(1)-12
(2)11
【解析】(1)利用乘法分配律进行去括号,再进行加减计算即可;
(2)先计算乘方,再计算乘除,最后进行加减计算即可.
(1)
解:原式=
=
=
(2)
原式=
=
=
此题考查了有理数的运算,掌握先计算乘方再计算乘除,最后计算加减的运算顺序,以及适当运用乘法分配律是解题的关键.
42.(1)26;(2).
【解析】(1)利用有理数乘法的分配律进行计算即可得;
(2)先计算有理数的乘方、绝对值,再计算有理数的乘除法,然后计算有理数的减法即可得.
(1)原式,
,
,
;
(2)原式,
,
,
,
.
本题考查了含乘方的有理数混合运算、绝对值、有理数乘法的分配律,熟练掌握运算法则和运算律是解题关键.
43.(1)-15;(2)-4
【解析】(1)先有理数乘方、绝对值运算,再有理数乘法运算,最后有理数加减运算即可求解;
(2)利用乘法分配律进行有理数乘法运算,再进行有理数加减法运算即可.
解:(1)-12-2+(-3)×
=-1-2+(-3)×4
=-1-2+(-12)
=-15;
(2)
=
=1-2-3
=-4.
本题考查有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
44.(1)
(2)-3
【解析】(1)直接利用乘法分配律计算得出答案;
(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可求出值.
(1)
原式==-12-+14=;
(2)
原式=-4-3÷(-3)=-4+1=-3.
本题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
45.(1)27;(2)-13.
【解析】(1)利用乘法分配律计算即可;
(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可求出值.
(1)原式==18-21+30=27;
(2)原式=-9-4=-13.
本题考查了含乘方的有理数的混合运算,熟练掌握运算法则是解本题的关键.
46.(1)7
(2)8
【解析】(1)解法一:按照从左到右的顺序依次计算;解法二:将正数、负数分别相加后再计算;
(2)先计算乘方,同时将除法化为乘法,再计算乘法,最后计算减法.
(1)
解:解法一:原式.
解:法二:原式.
(2)
解:原式.
此题考查了计算能力,有理数的加减混合运算和含乘方的有理数的混合运算,正确掌握有理数的计算法则及计算顺序是解题的关键.
47.(1);
(2).
【解析】(1)根据有理数的加减运算求解即可;
(2)根据有理数的乘方、乘除等运算求解即可.
(1)
解:;
(2)
此题考查了有理数的乘方、绝对值、加减乘除等四则运算,解题的关键是熟练掌握有理数的有关运算.
48.(1)-2
(2)5
【解析】(1)原式运用有理数加减法法则进行计算即可;
(2)原式先计算乘方和绝对值,再计算乘除法即可得到答案.
(1)
=
=
=-2;
(2)
=
=
=
=5
本题主要考查了有理数的混合运算,熟练掌握运算法则是解答本题的关键.
49.(1) 19
(2) 27
【解析】(1)先去括号,再计算加减法;
(2)先算乘方,再算乘法,最后算加减;同级运算,应按从左到右的顺序进行计算.
(1)
解:( 20)+(+3) ( 5) (+7)
= 20+3+5 7
= 19;
(2)
=2×( 27) 4×( 3)+15
= 54+12+15
= 27.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
1.(2022·江苏宿迁·七年级期末)如果规定符号“”的意义为,则的值是( )
A.5 B.-5 C.1 D.
2.(2022·江苏宿迁·七年级期末)取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明,但举例验证都是正确的.例如:取自然数5,经过下面5步运算可得1,即:如图所示.如果自然数m恰好经过7步运算可得到1,则所有符合条件的m的值有( )
A.6个 B.5个
C.4个 D.3个
3.(2022·江苏淮安·七年级期末)新华书店开业期间推出售书优惠方案:①一次性购书不超过100元,不享受优惠;②一次性购书超过100元但不超过200元一律打九折;③一次性购书200元律打八折.如李明明同学一次性购书付款162元,那么李明明所购书的原价一定为( )
A.180元 B.200 元
C.200元或202.5元 D.180元或202.5元
4.(2022·江苏扬州·七年级期末)如图,在这个数运算程序中,若开始输入的正整数n为奇数,都计算3n+1;若n为偶数,都除以2.若n=21时,经过1次上述运算输出的数是64;经过2次上述运算输出的数是32;经过3次上述运算输出的数是16;…;经过2022次上述运算输出的数是( ).
A.1 B.2 C.3 D.4
5.(2022·江苏宿迁·七年级期末)如图,是一个运算程序的示意图,若开始输入x的值为25,则第2022次输出的结果为_____.
6.(2022·江苏扬州·七年级期末)如图,输入数值1921,按所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),输出结果为_____.
7.(2022·江苏淮安·七年级期末)如图是一个数值运算程序,当输入的值为﹣2时,则输出的的值为 _____.
8.(2022·江苏扬州·七年级期末)如图是一个数值运算的程序,若输出y的值为1,则输入的值为____.
9.(2022·江苏南京·七年级期末)小明在计算1-3+5-7+9-11+13-15+17时,不小心把一个运算符号写错了(“+”错写成“-”或“-”错写成“+”),结果算成了-17,则原式从左往右数,第______个运算符号写错了.
10.(2022·江苏泰州·七年级期末)在如图所示的数值转换器中,如果输入的x、y满足,那么输出的结果为__________.
11.(2022·江苏无锡·七年级期末)我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.如图,一位妇女在从右到左依次排列的绳子上打结,满六进一,用来记录采集到的野果数量,由图可知,她一共采集到的野果数量为_____个.
12.(2022·江苏淮安·七年级期末)计算:
(1)2×(﹣2)+3
(2)
13.(2022·江苏泰州·七年级期末)计算:
(1);
(2).
14.(2022·江苏盐城·七年级期末)计算:
(1)
(2)
15.(2022·江苏无锡·七年级期末)计算:
(1);
(2)
16.(2022·江苏·苏州市振华中学校七年级期末)计算:
(1)
(2)
17.(2022·江苏淮安·七年级期末)计算:
(1);
(2)
18.(2022·江苏扬州·七年级期末)计算:
(1);
(2)
19.(2022·江苏南通·七年级期末)气象资料表明,高度每增加1000m,气温大约下降6℃.
(1)某山峰高1700m,当山脚的温度为时,求山顶气温;
(2)为估算某山峰的高度,两名研究人员同时在上午10点测得山脚和山顶的气温分别为9℃和-3℃,请估算此山峰的高度是多少米?
20.(2022·江苏扬州·七年级期末)某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中五次行驶记录如下(单位:千米):
第一次 第二次 第三次 第四次 第五次
﹣3 8 ﹣9 +10 ﹣2
(1)在第 次记录时距A地最远;
(2)收工时距A地 千米;
(3)若每千米耗油0.4升,每升汽油需6.5元,问检修小组工作一天需汽油费多少元?
21.(2022·江苏常州·七年级期末)(1)
(2)
22.(2022·江苏南京·七年级期末)计算:(1);
(2)
23.(2022·江苏南京·七年级期末)计算:
(1);
(2).
24.(2022·江苏南通·七年级期末)计算:
(1);
(2).
25.(2022·江苏·射阳县第六中学七年级期末)计算:
(1);
(2).
26.(2022·江苏常州·七年级期末)计算:
(1);
(2).
27.(2022·江苏苏州·七年级期末)计算:.
28.(2022·江苏无锡·七年级期末)计算:
(1)5×(﹣)﹣|﹣6|+(﹣3);
(2).
29.(2022·江苏·南京市第二十九中学七年级期末)计算:
(1)-14-[4-(-3)2] (2)(- +)×(-24)
30.(2022·江苏南京·七年级期末)计算:
(1);
(2).
31.(2022·江苏南通·七年级期末)计算:
(1);
(2).
32.(2022·江苏无锡·七年级期末)计算下列各题:
(1)23﹣(﹣7)+(﹣6);
(2).
33.(2022·江苏扬州·七年级期末)计算:
(1)
(2)
34.(2022·江苏南通·七年级期末)计算:
(1)﹣20+(+3)﹣(﹣5)﹣(+7);
(2)﹣2.5×(﹣);
(3)2×(﹣3)3﹣4×(﹣3)+15;
(4)(﹣2)3+(﹣3)×[(﹣4)3+2]﹣(﹣3)2÷(﹣2).
35.(2022·江苏宿迁·七年级期末)计算:
36.(2022·江苏江苏·七年级期末)计算:
(1);
(2).
37.(2022·江苏无锡·七年级期末)计算:
(1)12﹣(﹣18)+(﹣7)﹣15;
(2)(﹣1)2×(﹣23)﹣(﹣4)÷2×.
38.(2022·江苏·射阳县第六中学七年级期末)计算:
(1);
(2).
39.(2022·江苏·无锡市东林中学七年级期末)计算:
(1);
(2)
40.(2022·江苏扬州·七年级期末)计算:
(1)
(2)
41.(2022·江苏南京·七年级期末)计算:
(1)×(-18);
(2)-24-(-2)3÷×(-3)2.
42.(2022·江苏无锡·七年级期末)计算:
(1);
(2).
43.(2022·江苏南京·七年级期末)计算:
(1)-12-2+(-3)×;
(2).
44.(2022·江苏南京·七年级期末)计算:
(1);
(2).
45.(2022·江苏苏州·七年级期末)计算:
(1);
(2).
46.(2022·江苏徐州·七年级期末)计算:
(1)3+(-4)+6-(-2);
(2)2×(-3)2-5÷
47.(2022·江苏苏州·七年级期末)计算:
(1);
(2).
48.(2022·江苏泰州·七年级期末)计算
(1)
(2)
49.(2022·江苏南通·七年级期末)计算:
(1);
(2).
参考答案:
1.B
【解析】根据新定义代入,即可求解.
解:根据题意得:.
故选:B
本题主要考查了有理数的混合运算,理解新定义是解题的关键.
2.C
【解析】首先根据题意,应用逆推法,用1乘以2,得到2;用2乘以2,得到4;用4乘以2,得到8;用8乘以2,得到16;然后分类讨论,判断出所有符合条件的m的值为多少即可.
定义新运算
故答案为C
本题考查逆推法,熟练掌握计算法则是解题关键.
3.D
【解析】不享受优惠即原价,打九折即原价×0.9,打八折即原价×0.8.
解:∵200×0.9=180,200×0.8=160,160<162<180,
∴一次性购书付款162元,可能有两种情况.
162÷0.9=180元;162÷0.8=202.5元.
故王明所购书的原价一定为180元或202.5元.
故选:D.
本题考查有理数的运算在实际生活中的应用.注意售书有三种优惠方案.
4.B
【解析】分别求出部分输出结果,发现第1次输出结果到第4次输出结果只出现一次,从第5次输出结果开始,每3次结果循环一次,则经过2022次上述运算输出的数与第6次输出的结果相同,由此可求解.
解:当n=21时,
经过1次运算输出的数是64,
经过2次运算输出的数是32,
经过3次运算输出的数是16,
经过4次运算输出的数是8,
经过5次运算输出的数是4,
经过6次运算输出的数是2,
经过7次运算输出的数是1,
经过8次运算输出的数是4,
经过9次运算输出的数是2,
……
∴第1次输出结果到第4次输出结果只出现一次,从第5次输出结果开始,每3次结果循环一次,
∵(2022﹣4)÷3=672……2,
∴经过2022次上述运算输出的数与第6次输出的结果相同,
故选:B.
本题考查数字的变化规律,通过运算找到输出结果的循环规律是解题的关键.
5.1
【解析】由题意利用程序图进行运算,可以发现从第一次开始输出的结果以5,1为循环节循环,由此可得结论.
解:由题意得:
第一次输入25,输出结果为:5;
第二次输入5,输出结果为:1;
第三次输入1,输出结果为:5;
第四次输入5,输出结果为:1;
第五次输入1,输出结果为:5;
第六次输入5,输出结果为:1;
∴从第一次开始输出的结果以5,1为循环节循环,
∵2022÷2=1011,
∴第2022次输出的结果为:1.
故答案为:1.
本题主要考查了求代数式的值,有理数的混合运算,本题是操作型题目,理解并正确操作程序是解题的关键.
6.2021
【解析】把1921代入程序中计算,判断即可得到结果.
解:把1921代入得:(1921-1840+50)×(-1)=-131<1000,
把-131代入得:(-131-1840+50)×(-1)=1921>1000,
则输出结果为1921+100=2021.
故答案为:2021.
本题考查了有理数的混合运算,弄清程序中的运算过程是解本题的关键.
7.-18
【解析】把x=﹣2代入运算程序求值即可得最后结果.
解:把x=﹣2代入得,
(﹣2)2×(﹣5)+2
=4×(﹣5)+2
=﹣20+2
=﹣18,
故答案为:﹣18.
本题考查了代数式求值,有理数的混合运算,掌握运算程序的意义,读懂题意是解题关键.
8.
【解析】设输入的数为x,根据程序列出关于x的方程,求出x即可.
设输入的数为x,根据程序列方程得
÷2=1
故答案为
本题考查了整式的程序计算,正确理解程序是解题的关键.
9.6
【解析】先确定哪一个数的符号出了错,再确定这个符号是第几个.
∵1-3+5-7+9-11+13-15+17=9,
∴-17小于9,
∴一定是把+错写成减号了,
∴这个数为[9-(-17)]÷2=13,
∴是第六个符号写错了,
故答案为:6.
本题考查了有理数的混合运算,大小的比较,熟练进行计算是解题的关键.
10.0.5##
【解析】根据(2 x)2+|y+|=0,可以得到x、y的值,然后将x的值代入,求出最后可以输出的x的值即可.
解:∵,
∴2-x=0,y+=0,
解得x=2,y=-,
∴(-0.5)x=(-0.5)×2=-1<-,
当x=-1时,(-0.5)x=(-0.5)×(-1)=0.5>-,
故答案为:0.5.
本题考查有理数的混合运算、非负数的性质,解答本题的关键是求出最后的x的值.
11.1838
分析:类比于现在我们的十进制“满十进一”,可以表示满六进一的数为:万位上的数×64+千位上的数×63+百位上的数×62+十位上的数×6+个位上的数,即1×64+2×63+3×62+0×6+2=1838.
详解:2+0×6+3×6×6+2×6×6×6+1×6×6×6×6=1838,
故答案为1838.
点睛:本题是以古代“结绳计数”为背景,按满六进一计数,运用了类比的方法,根据图中的数学列式计算;本题题型新颖,一方面让学生了解了古代的数学知识,另一方面也考查了学生的思维能力.
12.(1)-1 ;
(2)7
【解析】(1)
解:2×(﹣2)+3
=-4+3
=-1
(2)
解:
此题主要考查了有理数的混合运算,熟悉运算法则是解题关键.
13.(1)
(2)4
【解析】(1)
解:
(2)
解:
本题考查了有理数的混合运算,解题的关键是掌握运算法则和运算顺序.
14.(1)15
(2)0
【解析】(1)先去括号去绝对值符号,再根据运算顺序,先算乘除再算加减;
(2)先去括号,根据运算顺序,先算乘方再算乘除再算加减;
(1)
解:原式=8-5+43
=8-5+12
=15
(2)
解:原式=-1+
=-1+1
=0
本题考查了有理数的混合运算,解题的关键是熟练掌握绝对值、乘方以及乘法的分配律,有理数相乘的时候可以根据同号正异号负的原则先确定符号再运算绝对值.
15.(1)-8
(2)5
【解析】(1)先计算乘法,再计算加减法;
(2)先计算乘方及乘法,再计算除法,最后计算加减法.
(1)
解:原式
.
(2)
解:原式
=-1+6
.
此题考查了有理数的混合运算及含乘方的有理数的混合运算,正确掌握运算顺序及运算法则是解题的关键.
16.(1)
(2)
【解析】(1)先算乘方,再算乘法,最后算减法;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;
(2)先算乘除,后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算;注意乘法分配律的运用.
(1)
解:
=
=
=
=
(2)
解:
=
=
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
17.(1)
(2)
【解析】(1)
解:
(2)
解:
本题考查的是含乘方的有理数的混合运算,掌握“有理数的混合运算的运算顺序”是解本题的关键,有理数的混合运算的运算顺序:先乘方,再乘除,最后算加减,有括号先算括号内的运算.
18.(1)18
(2)
【解析】(1)
(2)
本题考查了有理数的混合运算,掌握有理数的混合运算是解题的关键.
19.(1)7.8℃
(2)2000米
【解析】(1)由减去降低的温度即可;
(2)先计算出山脚与山顶的温差,再除以6,再乘以1000即可得到答案.
(1)解:℃.答:山顶气温7.8℃.
(2)解:m.答:此山峰的高度是2000m.
本题考查的是有理数的四则混合运算的实际应用,理解题意列出正确的运算式是解本题的关键.
20.(1)4
(2)4
(3)83.2
【解析】(1)五次行驶的和即收工时检修小组距离A地的距离;
(2)计算每一次记录检修小组离开A的距离,比较后得出检修小组距A地最远的次数;
(3)每次记录的绝对值的和,是检修小组一天的行程,根据单位行程的耗油量计算出该检修小组一天的耗油量.
(1)
第一次后,检修小组距A地3km;
第二次后,检修小组距A地 3+8=5(km);
第三次后,检修小组距A地 3+8 9= 4(km)
第四次后,检修小组距A地 3+8 9+10=6(km)
第五次后,检修小组距A地 3+8 9+10-2=4(km)
故在第四次记录时距A地最远
故答案为:4
(2)
3+8 9+10 2=4(km),
所以收工时距A地4 km
故答案为4;
(3)
(3+8+9+10+2)×0.4×6.5=83.2(元)
答:检修小组工作一天需汽油费83.2元.
本题考查了有理数的加减法在生活中的应用.解题的关键是熟知耗油量=行程×单位行程耗油量.
21.(1)26;(2)
解:(1)
;
(2)
,
,
,
;
本题考查了含乘方的有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
22.(1)40;(2)-4
【解析】(1)先算乘方,再算乘法,最后算加法;
(2)先算乘方,再算除法,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有绝对值,要先做绝对值内的运算.
解:(1)原式=4+36
=40;
(2)原式=-1+6-9
=-4.
考查了有理数混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
23.(1)27;(2)-11;
【解析】(1)先利用乘法分配律并去括号,在进行加减运算;
(2)先算括号里面的,再算括号外面的算式,括号内先算乘法再算加减.
(1)解:原式
.
(2)解:原式
.
有理数的混合运算,应注意运算顺序,先乘方,再乘除,再加减,有括号先算括号.
24.(1)8
(2)
【解析】(1)去括号后再计算即可;
(2)先乘方,再乘除,最后加减,计算即可.
(1)
解:
∴原式的值为.
(2)
解:
∴原式的值为.
本题考查了整式的加减,分数的混合运算,同分母分数加减,有理数的乘方等知识.解题的关键在于正确的去括号与乘除运算.
25.(1)-5
(2)15
【解析】(1)利用乘法分配律展开计算即可;
(2)先算乘方,和绝对值,再算除法,最后算加减.
(1)
解:
=
=
=
(2)
=
=
=
本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
26.(1);
(2).
【解析】(1)先计算乘法,再加减即可;
(2)先计算绝对值,乘方,再计算加减即可.
(1)
解:,
=,
=;
(2)
解:,
=,
=.
本题考查含乘方的有理数混合运算,掌握含乘方的有理数混合运算法则,先乘方,再乘除,最后加减,有括号先小括号,中括号再大括号是解题关键.
27.9
【解析】先算括号,再计算乘方,然后计算乘除,最后计算加减.
解:
.
本题考查含乘方的有理数的混合运算,是重要考点,掌握相关知识是解题关键.
28.(1)-11;
(2)-3.
【解析】(1)先算乘法,后算加减;同级运算,应按从左到右的顺序进行计算;如果有绝对值,要先做绝对值内的运算;
(2)先算乘方,再算除法,最后算加法;同级运算,应按从左到右的顺序进行计算.
(1)
解:5×(-)-|-6|+(-3)
=-2-6-3
=-11;
(2)
解:( 1)2002÷+42+( 3)3
=1÷+16-27
=1×8+16-27
=8+16-27
=-3.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
29.(1)4;(2)-22
【解析】(1)先计算乘方,再计算加减法;
(2)根据乘法分配律计算.
解:(1)-14-[4-(-3)2]
=-1-(-5)
=4;
(2)(- +)×(-24)
=×(-24)-×(-24)+×(-24)
=-6+20-36
=-22.
此题考查了有理数的计算,正确掌握含乘方的有理数的混合运算法则、乘法分配律法则是解题的关键.
30.(1)
(2)
【解析】(1)
解:
(2)
解:
.
本题主要考查了有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
31.(1)-3.8
(2)
【解析】(1)
解:原式;
(2)
解:原式.
本题主要考查了有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
32.(1)24
(2)﹣6
【解析】(1)根据有理数的加减运算法则进行计算即可;
(2)先算乘方,再算括号内运算,再算乘法,最后算减法即可.
(1)解:23﹣(﹣7)+(﹣6)=23+7﹣6=30﹣6=24
(2)解:
本题考查有理数的混合运算,要熟练掌握运算法则,注意运算顺序.
33.(1)-3
(2)1
【解析】(1)
解:
(2)
解:
本题考查的是含乘方的有理数的混合运算,有理数乘法的分配律的应用,掌握“有理数的混合运算的运算顺序”是解本题的关键,有理数的混合运算的运算顺序为:先乘方,再乘除,最后算加减,有括号先计算括号内的运算.
34.(1)-19;
(2)1;
(3)-27;
(4)182.5.
【解析】(1)
解:﹣20+(+3)﹣(﹣5)﹣(+7)
=-20+3+5-7
=-19;
(2)
解:﹣2.5×(﹣)
=-××(-)
=1;
(3)
解:2×(﹣3)3﹣4×(﹣3)+15
=2×(-27)+12+15
=-54+12+15
=-27;
(4)
解:(﹣2)3+(﹣3)×[(﹣4)3+2]﹣(﹣3)2÷(﹣2)
=-8+(﹣3)×(﹣64+2)-9÷(﹣2)
=-8+(﹣3)×(﹣62)+9÷2
=-8+186+4.5
=182.5.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
35.23
【解析】先计算乘方、绝对值,然后计算乘除,最后计算加减,即可得到答案.
解:
本题考查了有理数的混合运算.解题的关键在于明确先计算乘方、绝对值,然后计算乘除,最后计算加减.
36.(1)
(2)0
【解析】(1)先把除法转化为乘法,再利用乘法的运算法则求解即可;
(2)先算乘方,再进行括号里的运算,接着算乘法,最后算加法即可.
(1)
解:
=(﹣12)×(﹣)×
=;
(2)
解:
=﹣1﹣×(5﹣9)
=﹣1﹣×(﹣4)
=﹣1+1
=0.
本题主要考查有理数的混合运算,解答的关键是对相应的运算法则的掌握.
37.(1)8;
(2)-7.
【解析】(1)
解:12﹣(﹣18)+(﹣7)﹣15
=12+18-7-15
=8;
(2)
解:(﹣1)2×(﹣23)﹣(﹣4)÷2×
=1×(﹣8)+4××
=-8+1
=-7.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
38.(1)
(2)
【解析】(1)
(2)
本题考查了有理数的混合运算,正确的计算是解题的关键.
39.(1)-12;
(2)18
【解析】(1)
解:
=-12;
(2)
解:
=18.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
40.(1)-6 ;(2)15
【解析】(1)利用减法法则变形,进行计算即可求解;
(2)先计算乘方,再利用有理数的乘方运算律计算乘法,最后计算加减,即可求解.
解:(1)
;
(2)
.
本题主要考查了有理数的混合运算,熟练掌握相关运算法则是解题的关键.
41.(1)-12
(2)11
【解析】(1)利用乘法分配律进行去括号,再进行加减计算即可;
(2)先计算乘方,再计算乘除,最后进行加减计算即可.
(1)
解:原式=
=
=
(2)
原式=
=
=
此题考查了有理数的运算,掌握先计算乘方再计算乘除,最后计算加减的运算顺序,以及适当运用乘法分配律是解题的关键.
42.(1)26;(2).
【解析】(1)利用有理数乘法的分配律进行计算即可得;
(2)先计算有理数的乘方、绝对值,再计算有理数的乘除法,然后计算有理数的减法即可得.
(1)原式,
,
,
;
(2)原式,
,
,
,
.
本题考查了含乘方的有理数混合运算、绝对值、有理数乘法的分配律,熟练掌握运算法则和运算律是解题关键.
43.(1)-15;(2)-4
【解析】(1)先有理数乘方、绝对值运算,再有理数乘法运算,最后有理数加减运算即可求解;
(2)利用乘法分配律进行有理数乘法运算,再进行有理数加减法运算即可.
解:(1)-12-2+(-3)×
=-1-2+(-3)×4
=-1-2+(-12)
=-15;
(2)
=
=1-2-3
=-4.
本题考查有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
44.(1)
(2)-3
【解析】(1)直接利用乘法分配律计算得出答案;
(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可求出值.
(1)
原式==-12-+14=;
(2)
原式=-4-3÷(-3)=-4+1=-3.
本题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
45.(1)27;(2)-13.
【解析】(1)利用乘法分配律计算即可;
(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可求出值.
(1)原式==18-21+30=27;
(2)原式=-9-4=-13.
本题考查了含乘方的有理数的混合运算,熟练掌握运算法则是解本题的关键.
46.(1)7
(2)8
【解析】(1)解法一:按照从左到右的顺序依次计算;解法二:将正数、负数分别相加后再计算;
(2)先计算乘方,同时将除法化为乘法,再计算乘法,最后计算减法.
(1)
解:解法一:原式.
解:法二:原式.
(2)
解:原式.
此题考查了计算能力,有理数的加减混合运算和含乘方的有理数的混合运算,正确掌握有理数的计算法则及计算顺序是解题的关键.
47.(1);
(2).
【解析】(1)根据有理数的加减运算求解即可;
(2)根据有理数的乘方、乘除等运算求解即可.
(1)
解:;
(2)
此题考查了有理数的乘方、绝对值、加减乘除等四则运算,解题的关键是熟练掌握有理数的有关运算.
48.(1)-2
(2)5
【解析】(1)原式运用有理数加减法法则进行计算即可;
(2)原式先计算乘方和绝对值,再计算乘除法即可得到答案.
(1)
=
=
=-2;
(2)
=
=
=
=5
本题主要考查了有理数的混合运算,熟练掌握运算法则是解答本题的关键.
49.(1) 19
(2) 27
【解析】(1)先去括号,再计算加减法;
(2)先算乘方,再算乘法,最后算加减;同级运算,应按从左到右的顺序进行计算.
(1)
解:( 20)+(+3) ( 5) (+7)
= 20+3+5 7
= 19;
(2)
=2×( 27) 4×( 3)+15
= 54+12+15
= 27.
本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
