2021-2022学年江苏省各地苏科版数学七年级上册3.2代数式期末试题分类选编(Word版含答案)
文档属性
| 名称 | 2021-2022学年江苏省各地苏科版数学七年级上册3.2代数式期末试题分类选编(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 891.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 17:13:50 | ||
图片预览




文档简介
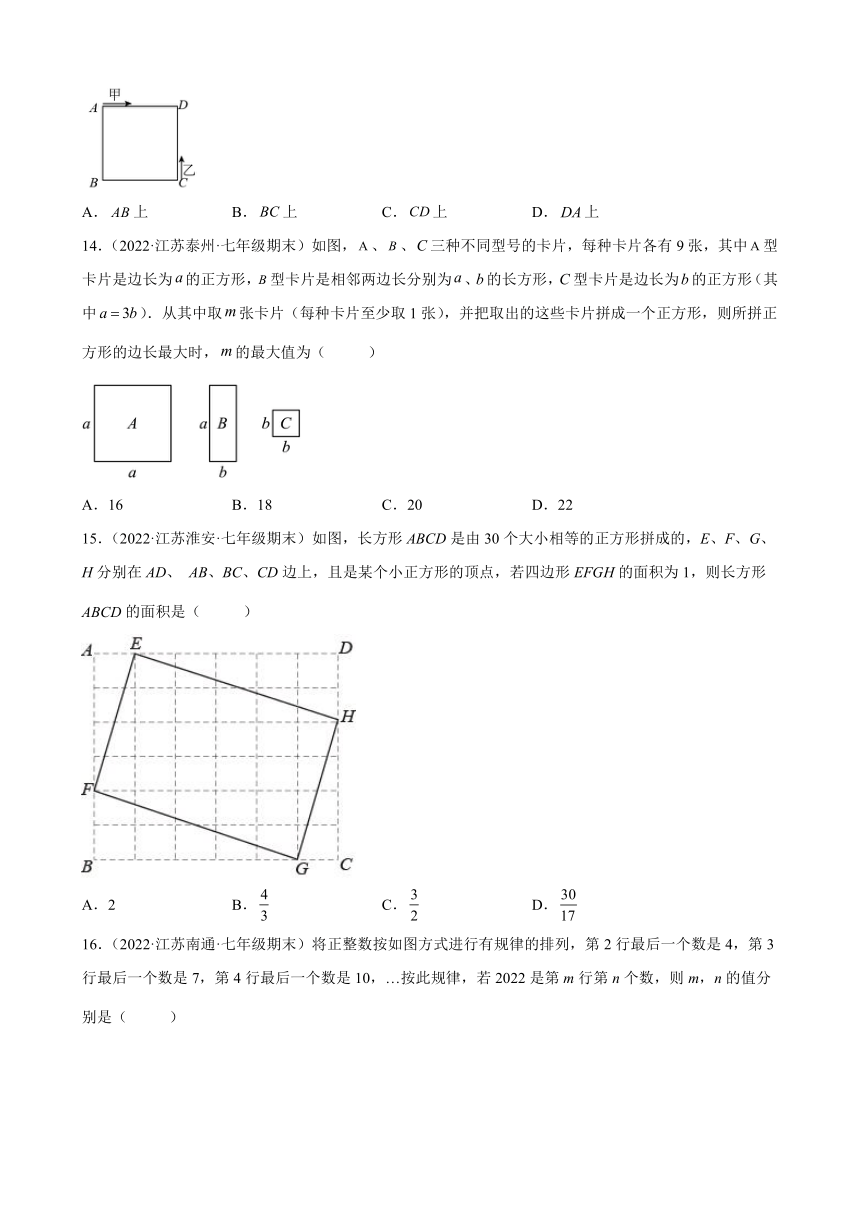
3.2 代数式
1.(2022·江苏无锡·七年级期末)下列说法错误的是( )
A.2x2-3xy-1是二次三项式 B.﹣x+1不是单项式
C.﹣的系数是﹣ D.﹣22xa3b2的次数是6
2.(2022·江苏盐城·七年级期末)如果整式是关于的二次三项式,那么等于( )
A.3 B.4 C.5 D.6
3.(2022·江苏南通·七年级期末)有18m长的木料,要做成一个如图的窗框.如果窗框横档的长度为xm,窗框厚度忽略不计,那么窗户的面积是( )
A. B. C. D.
4.(2022·江苏南通·七年级期末)某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )
A.万元 B.万元
C.万元 D.万元
5.(2022·江苏常州·七年级期末)甲、乙、丙三家超市同时为促销某种定价一样的相同商品,甲超市直接一次性降价30%,乙超市先降价20%,再降价10%:丙超市连续两次降价15%,那么顾客要买这件商品,到哪家超市购买更合算( )
A.甲 B.乙 C.丙 D.三家都一样
6.(2022·江苏无锡·七年级期末)今年苹果的单价比去年便宜了10%,已知今年苹果的单价是每千克a元,则去年苹果的单价是( )
A.10%a B. C. D.
7.(2022·江苏盐城·七年级期末)用代数式表示“的2倍与3的差”为( )
A. B. C. D.
8.(2022·江苏泰州·七年级期末)下列关于“代数式”的意义叙述正确的有( )个.
①x的4倍与y的2倍的和是;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元.
A.3 B.2 C.1 D.0
9.(2022·江苏南京·七年级期末)下列语句中,不正确的是( )
A.0是单项式 B.多项式的次数是4
C.的系数是 D.的系数和次数都是1
10.(2022·江苏宿迁·七年级期末)符号“”表示一种运算,运算规律如下:,,,,…,则( )
A. B. C. D.
11.(2022·江苏淮安·七年级期末)有一个正方体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的点数是( )
A.5 B.3 C.4 D.2
12.(2022·江苏盐城·七年级期末)如图所示的图形是由正方形和相同大小的圆按照一定规律摆放而成,按此规律,若要得到604个圆,则为第( )个图形.
A.200 B.201 C.202 D.302
13.(2022·江苏·苏州市振华中学校七年级期末)如图,甲、乙两动点分别从正方形的顶点、同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2000次相遇在边( )
A.上 B.上 C.上 D.上
14.(2022·江苏泰州·七年级期末)如图,、、三种不同型号的卡片,每种卡片各有9张,其中型卡片是边长为的正方形,型卡片是相邻两边长分别为、的长方形,型卡片是边长为的正方形(其中).从其中取张卡片(每种卡片至少取1张),并把取出的这些卡片拼成一个正方形,则所拼正方形的边长最大时,的最大值为( )
A.16 B.18 C.20 D.22
15.(2022·江苏淮安·七年级期末)如图,长方形ABCD是由30个大小相等的正方形拼成的,E、F、G、H分别在AD、 AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则长方形ABCD的面积是( )
A.2 B. C. D.
16.(2022·江苏南通·七年级期末)将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,…按此规律,若2022是第m行第n个数,则m,n的值分别是( )
A., B.,
C., D.,
17.(2022·江苏无锡·七年级期末)在一列数:a1,a2,a3,…,an中,a1=1,a2=2,a3=4,从第四个数开始,每一个数都等于它前三个数之积的个位数字,则这一列数中的第2022个数是( )
A.2 B.4 C.6 D.8
18.(2022·江苏南京·七年级期末)在某多媒体电子杂志的某一期上刊登了“正方形雪花图案的形成”的演示案例:作一个正方形,设每边长为4a,将每边四等分,作一凸一凹的两个边长为a的小正方形,得到图形如图(2)所示,称为第一次变化,再对图(2)的每个边做相同的变化,得到图形如图(3),称为第二次变化,如此连续作几次,便可得到一个绚丽多彩的雪花图案.如不断发展下去到第n次变化时,图形的面积和周长分别为( )
A.和 B.和 C.和 D.和
19.(2022·江苏盐城·七年级期末)把一个两位数交换十位数字和个位数字后得到一个新的两位数,若将这个新的两位数与原两位数相加,则所得的和一定是( )
A.11的倍数 B.奇数 C.偶数 D.9的倍数
20.(2022·江苏南通·七年级期末)一个两位数个位为a,十位数字为b,这个两位数为_____.
21.(2022·江苏淮安·七年级期末)的3倍与的差用代数式表示为______.
22.(2022·江苏南京·七年级期末)单项式的系数是______.
23.(2022·江苏扬州·七年级期末)单项式的系数是____.
24.(2022·江苏盐城·七年级期末)单项式﹣23xy3的次数是 _____.
25.(2022·江苏泰州·七年级期末)的系数是_______.
26.(2022·江苏常州·七年级期末)单项式-3的系数是_________.
27.(2022·江苏·射阳县第六中学七年级期末)单项式﹣2πa2bc的次数为 _____.
28.(2022·江苏盐城·七年级期末)单项式的系数为__________.
29.(2022·江苏无锡·七年级期末)写出一个含有字母a,b的三次单项式:________.
30.(2022·江苏南京·七年级期末)多项式a2b+2ab+b+1的次数是______.
31.(2022·江苏无锡·七年级期末)多项式2x2y﹣x3+5x2x2的次数是_____.
32.(2022·江苏·南京市第二十九中学七年级期末)多项式x3-4x2y3+26的次数是_______.
33.(2022·江苏·无锡市东林中学七年级期末)多项式2a2b-abc的次数是______.
34.(2022·江苏无锡·七年级期末)某校开展了丰富多彩的社团活动,每位学生可以选择自己最感兴趣的一个社团参加.已知参加体育类社团的有m人,参加文艺类社团的人数比参加体育类社团的人数多6人,参加科技类社团的人数比参加文艺类社团人数的多2人,则参加三类社团的总人数为_________(用m的代数式表示)
35.(2022·江苏常州·七年级期末)七巧板被西方人称为“东方魔术”,下面的两幅图是由同一个七巧板拼成的.已知七巧板拼成的正方形(如图1)边长为,则图2的“小狐狸”图案中阴影部分面积是____(用含的代数式表示).
36.(2022·江苏泰州·七年级期末)单项式的系数为______.
37.(2022·江苏宿迁·七年级期末)单项式﹣5xy2的次数是 _____.
38.(2022·江苏南京·七年级期末)写出一个系数为﹣5且含x,y的三次单项式_____.
39.(2022·江苏扬州·七年级期末)多项式的次数是_______.
40.(2022·江苏常州·七年级期末)若多项式3xa+3﹣x3﹣a+4是四次三项式,则a=____.
41.(2022·江苏扬州·七年级期末)若是关于的二次二项式,那么的值为______.
42.(2022·江苏南通·七年级期末)若关于、的多项式是二次三项式,则_______.
43.(2022·江苏江苏·七年级期末)若3x|m|﹣(2+m)x+5是关于x的二次三项式,那么m的值为 ___.
44.(2022·江苏扬州·七年级期末)如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右从小到大,且相邻两个点所表示的数相差1,每行数的和等于右边相应的数字.那么表示2022的点在第____行位置.
45.(2022·江苏盐城·七年级期末)如表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2022个格子中的数为________.
3 2 …
46.(2022·江苏扬州·七年级期末)某地铺设矩形人行道,由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3);以此类推.
现在街道上铺设一条这样的人行道,一共有(为正整数)块正方形地砖,则等腰直角三角形地砖的块数为_______(用含的代数式表示)
47.(2022·江苏扬州·七年级期末)观察:第1个等式,第2个等式,第3个等式,第4个等式…猜想:第n个等式是________.
48.(2022·江苏南京·七年级期末)有一数值转换器,原理如图所示,如果开始输入x的值是34,则第一次输出的结果是17,第二次输出的结果是52,……,那么第2022次输出的结果是_________.
49.(2022·江苏苏州·七年级期末)王老师在教学过程中善于把数学知识与实际生活联系在一起.在课堂上,他把全班同学分成五组,编号分别是A、B、C、D、E,每组的人数分别是10、6、7、9、8.游戏规则:当他数完1后,人数最少的那一组学生不动,其他各组各出一个人去人数最少的那组;当他数完2后,此时人数最少的那一组学生不动,其他各组再各出一个人去人数最少的那组;……如此进行下去,那么如果当王老师数完2022后,C组中的人数是_______.
50.(2022·江苏盐城·七年级期末)如图,“海春书局”把WIFI密码做成了数学题.小红在海春书局看书时,思索了一会儿,输入密码,顺利地连接到了“海春书局”的网络,那么她输入的密码是__________.
51.(2022·江苏连云港·七年级期末)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为8的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为___________.
52.(2022·江苏泰州·七年级期末)在无限大的正方形网格中按规律涂成的阴影如图所示,第1、2、3个图中阴影部分小正方形的个数分别为6个、11个、18个,根据此规律,则第20个图中阴影部分小正方形的个数是__________.
53.(2022·江苏淮安·七年级期末)用同样大小的两种不同颜色的正方形纸片,按如图方式拼成正方形.第90个比第89个多___个小正方形纸片.
54.(2022·江苏南京·七年级期末)如图,红黄绿三块一样大的正方形纸片放在一个正方形盒内,它们之间互相重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是13,绿色的面积是11,则正方形盒子的面积为_____________.
55.(2022·江苏镇江·七年级期末)观察下列式子:
①,
②,
③,
……
(1)根据你发现的规律,请写出第个等式________;
(2)根据你发现的规律,请写出第(为正整数)个等式________,并证明你所写出的等式的正确性;
(3)请写出第198个等式:_________.
56.(2022·江苏淮安·七年级期末)用正方形的白色水泥砖和灰色水泥砖按如图所示的方式铺人行道
(1)第①个图中有灰色水泥砖 块,
第②个图中有灰色水泥砖 块,
第③个图中有灰色水泥砖 块;
(2)依次铺下去,第n个图中有灰色水泥砖 块.
参考答案:
1.C
【解析】根据单项式的个数就是多项式的项数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式,再结合单项式的次数与系数确定方法,进而得出答案.
解:A、2x2-3xy-1是二次二项式,正确,故此选项不合题意;
B、-x+1不是单项式,正确,故此选项不合题意;
C、的系数是,原说法错误,故此选项符合题意;
D、22xa3b2的次数是6,正确,故此选项不合题意;
故选:C.
本题主要考查了多项式与单项式,正确掌握多项式的项数与次数确定方法是解题关键.
2.B
【解析】由于该多项式是关于x的二次三项式,可得n-2=2,即可求得n的值.
解:∵多项式是关于x的二次三项式,
∴n-2=2,
解得n=4,
故选:B.
本题考查了根据多项式的次数求参数的值,理解二次三项式的含义是解决本题的关键.
3.B
【解析】根据题意可知:用18m长的木料做成一个窗框,也就是它的周长是18m,已知窗框横档的长度为xm,那么窗框长为(18-3x)÷2=9-1.5x(m),根据长方形的面积=长×宽,把数据代入公式解答.
解:因为窗框横档的长度为xm,则显然窗框的长是(18-3x)÷2=9-1.5x(m),
∴窗户的面积是
故选:B
本题考查了列代数式,特别注意窗框的横档有3条边.解决问题的关键是读懂题意,找到所求的量的等量关系.
4.C
【解析】根据2月份比1月份减少了15%,可求出2月份的产值为a(1-15%),再由3月份比2月份增加了5%,列式即可得答案.
∵1月份产值为a万元,2月份比1月份减少了15%,
∴2月份的产值为a(1 15%),
∵3月份比2月份增加了5%,
∴3月份的产值为a(1-15%)(1+5%),
故选:C.
本题主要考查了列代数式,明确题意,用a表示出2月份、3月份的产值是解题的关键.
5.A
【解析】根据题意设商品的定价为,分别求得甲、乙、丙三家的售价,进而比较大小即可求解.
解:设商品的定价为,则甲超市的售价为:,
乙超市的售价为:
丙超市的售价为:
甲超市购买更合算
故选A
本题考查了列代数式,理解题意,列出代数式是解题的关键.
6.D
【解析】根据:去年的单价×(1-10%)=今年的单价,代入数据可求得去年的单价.
解:由题意得,去年的单价×(1-10%)=a,
则去年的单价=.
故选:D.
本题考查列代数式,关键是知道今年的单价和去年单价的关系,从而列出代数式.
7.B
【解析】先表示的2倍为,然后再减去3即可.
解:由题意得,的2倍与3的差表示为:.
故选:B.
本题考查了列代数式,解题的关键是正确理解文字语言中的关键词,比如该题中的“倍”、“差”等,从而明确其中的运算关系,正确列出代数式.
8.B
【解析】根据代数式的意义分别对三个叙述进行判断即可.
解:①x的4倍与y的2倍的和是,正确;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米,正确;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元,错误;
故正确的有2个
故选:B.
此题考查了代数式的问题,解题的关键是掌握代数式的意义以及性质.
9.D
【解析】分别根据单独一个数也是单项式、多项式中每个单项式的最高次数是这个多项式的次数、单项式中的数字因数是这个单项式的系数、单项式中所有字母的指数和是这个单项式的次数解答即可.
解:A、0是单项式,正确,不符合题意;
B、多项式的次数是4,正确,不符合题意;
C、的系数是,正确,不符合题意;
D、的系数是-1,次数是1,错误,符合题意,
故选:D.
本题考查单项式、单项式的系数和次数、多项式的次数,理解相关知识的概念是解答的关键.
10.D
【解析】根据题意得到规律,从而得到,即可求解.
解:根据题意得:,
,
,
,
……,
由此发现,,
∴
.
故选:D
本题主要考查了数字类规律题,明确题意,准确得到规律是解题的关键.
11.B
【解析】观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,从而确定答案.
解:观察图形知道点数三和点数四相对,点数二和点数五相对且滚动四次一循环,
,
滚动第2022次后与第2次相同,
朝下的数字是4的对面3,
故选:B.
本题考查了正方体相对两个面上的文字及图形的变化类问题,解题的关键是发现规律.
12.B
【解析】观察图形的变化找到规律,再代入求解即可.
解:观察图形的变化可知.
第1个图形中圆的个数为4;
第2个图形中圆的个数为4+3=4+3×1=7;
第3个图形中圆的个数为4+3+3=4+3×2=10;
…
则第n个图形中圆的个数为4+3×(n﹣1)=3n+1.
当有604个圆时,得3n+1=604,
解得:n=201.
故选:B.
本题考查图形类规律,正确观察图形的变化是解题关键.
13.A
【解析】此题利用行程问题中的相遇问题,根据乙的速度是甲的速度的4倍,求得每一次相遇的地点,找出规律即可解答.
解:根据题意分析可得:乙的速度是甲的速度的4倍,故第1次相遇,甲走了正方形周长的 ;
从第2次相遇起,每次甲走了正方形周长的 ,
从第2次相遇起,5次一个循环.
因此可得:从开始出发起,每次相遇的位置依次是:AD,DC,点C,CB,BA;依次循环.
∵2000-1=1999,
1999÷5=399余4,
故它们第2000次相遇位置在边AB上.
故选:A.
本题主要考查了规律型的题目,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
14.C
【解析】根据题意每种卡片各有9张,每种至少取1张,拼成的正方形的边长要最大,则每种卡片应尽量多取,而全部用完时三种卡片的面积和为,则边长不是整数无法拼成.那么只需要面积比小,又是平方数即可,所以最大面积为,边长为10.
解:型卡片的面积为9b2,型卡片的面积为3b2,型卡片的面积为b2,
拼成的正方形的边长要最大,
拼成的正方形面积要最大,
,
,
当拼成的正方形面积为时最大,则边长为10,
此时:型9张,型6张,型1张,共16张;
型9张,型5张,型4张,共18张;
型9张,型4张,型7张,共20张;
故选:C.
本题主要考查了多项式乘多项式的运算方法,解题的关键是熟练掌握运算法则.
15.D
【解析】设每个小正方形的边形为,根据三角形的面积公式即可求出,的值,由此即可用含的代数式表示出四边形EFGH的面积,再根据四边形EFGH的面积为1即可求出,从而可得出结论.
解:设每个小正方形的边形为,
则:
,
∴四边形EFGH的面积=
∴
∴矩形ABCD的面积=
故选:D.
本题考查了矩形的性质、三角形的面积、矩形的面积以及利用平方根解一元二次方程,根据四边形EFGH的面积为1求出是解题的关键.
16.C
【解析】根据前4行归纳类推出每一行第1个数和最后一个数的一般规律,再结合每一行相邻两个数之差为1,由此即可得出答案.
解:由图可知,第1行第1个数为1,最后一个数为1,
第2行第1个数为2,最后一个数为,
第3行第1个数为3,最后一个数为,
第4行第1个数为4,最后一个数为,
归纳类推得:第行第1个数为,最后一个数为,
因为,
所以2022在第675行,即,
又因为第675行第1个数为675,且每一行相邻两个数之差为1,
所以,
故选:C.
本题考查了数字类规律探索,正确归纳类推出一般规律是解题关键.
17.D
【解析】可分别求出前12个数的情况,观察它是否具有周期性,再把2022代入求解即可.
解:依题意得:a1=1,a2=2,a3=4,
∵从第四个数开始,每一个数都等于它前三个数之积的个位数字,
∴1×2×4=8,即a4=8,
2×4×8=64,即a5=4,
4×8×4=128,即a6=8,
8×4×8=256,即a7=6,
4×8×6=192,即a8=2,
8×6×2=96,即a9=6,
6×2×6=72,即a10=2,
2×6×2=24,即a11=4,
6×2×4=48,即a12=8,
...,
即从第2个数开始,以2,4,8,4,8,6,2,6这8个数不断循环出现,
∵(2022-1)÷8=252......5,
∴第2022个数为8.
故选:D.
本题考查了找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.而具有周期性的题目,找出周期是解题的关键.
18.B
【解析】观察图形,发现对正方形每进行1次分形,周长增加1倍;每增加一个小正方形同时又减少一个相同的小正方形,即面积不变.
解:周长依次为32a,64a,128a,…,2n+4a,即无限增加,
所以不断发展下去到第n次变化时,图形的周长为2n+4a;
图形进行分形时,每增加一个小正方形同时又减少一个相同的小正方形,即面积不变,是一个定值16a2.
故选:B.
此题考查了图形的变化类,主要培养学生的观察能力和概括能力,观察出后一个图形的周长比它的前一个增加1倍是解题的关键,本题有一定难度.
19.A
【解析】用字母设出原两位数的十位数字和个位数字,表示出原两位数和新两位数的和,进行因式分解,看是哪个常数的倍数即可.
解:设原两位数十位上的数字是a,个位上的数字是b,则原两位数为10a+b,新两位数为10b+a,
∴这两个数的和为11a+11b=11(a+b),
∴所得的和一定是11的倍数,
故选:A.
本题考查了列代数式;注意两位数的表示方法为:10×十位数字+个位数字.
20.(10b+a)## (a+10b)
【解析】用十位上的数字乘以10,加上个位上的数字,即可列出这个两位数.
解:由题意得:这个两位数是:10b+a.
故答案为:(10b+a).
本题考查列代数式问题,解决本题的关键是根据各个数位上的数所表示的意义,能用字母表示一个数.
21.
【解析】根据题意,列出代数式,即可得到答案.
解:根据题意,得:;
故答案为:.
本题考查了列代数式,解题的关键是正确理解题意,列出代数式.
22.##0.5
【解析】根据单项式的系数的概念解答.
单项式的数字因数是
∴单项式的系数是.
故答案为:.
本题考查了单项式的系数的概念:单项式中的数字因数叫做单项式的系数.正确理解概念是解题的关键.
23.
【解析】单项式的系数就是所含字母前面的因数,由此即可求解.
解: 单项式的系数是.
故答案为:
本题考查单项式的系数的定义,解题关键是熟练掌握相关的定义即可求解.
24.
【解析】直接利用一个单项式中所有字母的指数的和叫做单项式的次数,进而得出答案.
解:单项式的次数是.
故答案为: .
本题主要考察单项式的概念,掌握单项式的概念是解题的关键.
25.
【解析】根据单项式的系数的定义进行解答即可.
解∶的系数是.
故答案为:.
本题考查的是单项式的系数,即单项式中的数字因数叫做单项式的系数.
26.
【解析】根据单项式中的数字因数是单项式的系数去确定,不要忽视数的符号.
∵单项式-3的系数是-3,
故答案为:-3.
本题考查了单项式的系数即单项式中的数字因数,准确理解定义是解题的关键.
27.4
【解析】根据单项式的次数的定义得出即可.
解:-2πa2bc单项式的次数是2+1+1=4,
故答案为:4.
本题考查了单项式的次数的定义,能熟记单项式的次数的定义的内容是解此题的关键,注意:单项式中的字母的指数的和,叫单项式的次数.
28.
【解析】根据单项式中的数字因数叫单项式的系数可得到答案
解:中的数字因数为
故答案为
本题考查了单项式的系数这个知识点,熟练掌握单项式系数概念是解题的关键.
29.(答案不唯一)
【解析】单项式中所有字母的指数和是单项式的次数,根据定义结合单项式含,从而可得答案.
解:含有字母a,b的三次单项式有:,
故答案为: (答案不唯一)
本题考查的是单项式的次数,掌握“单项式的次数”是解本题的关键.
30.3
【解析】分别求出多项式各项的次数,次数最高项的次数即为所求.
解:a2b+2ab+b+1各项次数分别为3、2、1、0,
故多项式的次数为3,
故答案为3.
本题考查多项式的次数,多项式中次数最高项的次数是多项式的次数.
31.4
【解析】根据多项式的次数是多项式中次数最高的单项的次数解答即可.
解:多项式2x2y﹣x3+5x2x2的次数是4次;
故答案为:4.
本题考查了多项式,利用了多项式的次数的定义是关键.确定多项式的次数,就是确定多项式中次数最高的项的次数.
32.5
【解析】根据多项式次数的定义解答.
解:多项式各项的次数分别为:3、5、0,
故答案为:5.
此题考查了多项式次数的定义:多项式中次数最高项的次数是多项式的次数,熟记定义是解题的关键.
33.3
【解析】利用几个单项式的和叫做多项式,每个单项式叫做多项式的项,多项式中次数最高的项的次数叫做多项式的次数,据此求解即可.
解:多项式2a2b-abc的次数是3.
故答案为:3.
本题主要考查了多项式,正确把握多项式的项数和次数确定方法是解题关键.
34.(m+11)
【解析】利用题干中的数量关系分别表示出参加文艺类社团的人数和参加科技类社团的人数,将参加三类社团的人数相加即可得出结论.
解:∵参加文艺类社团的人数比参加体育类社团的人数多6人,
∴参加文艺类社团的人数为:(m+6)人.
∵参加科技类社团的人数比参加文艺类社团人数的多2人,
∴参加科技类社团的人数为:(m+6)+2=(m+5)人.
∴参加三类社团的总人数为:m+(m+6)+(m+5)=(m+11)人.
故答案为:(m+11).
本题主要考查了列代数式,分别求出参加文艺类社团的人数和参加科技类社团的人数是解题的关键.
35.
【解析】由图可知,阴影部分面积为正方形面积的一半.
解:正方形的面积为,
∵阴影部分面积为正方形面积的一半
∴阴影部分面积为,
故答案为:.
本题主要列代数式,观察图形得出阴影部分为七巧板的右上部分是解题关键.
36.
【解析】根据单项式中的数字因数叫做单项式的系数求解.
单项式的系数为,
故答案为:.
本题考查了单项式:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式;单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.
37.3
【解析】单项式中所有字母指数的和是单项式的次数,根据定义解答.
解:单项式﹣5xy2的次数是1+2=3,
故答案为:3.
此题考查了单项式的次数定义,熟记定义是解题的关键.
38.-5x2y(答案不唯一)
【解析】根据单项式的系数和次数的概念求解即可.
-5x2y是一个系数为﹣5且含x,y的三次单项式,故答案为-5x2y(答案不唯一).
本题考查单项式的概念,单项式中的数字因数叫做单项式的系数,单项式中所有字母的指数和叫做单项式的次数.
39.5
【解析】根据多项式的次数的定义分析即可,多项式的每一项都有次数,其中次数最高的项的次数,就是这个多项式的次数.
解:多项式的次数是的次数,是.
故答案为:5.
本题考查了多项式的次数,理解多项式的次数的定义是解题的关键.
40.﹣1或1##1或-1
【解析】根据题意可得:①a+3=4,4≥3 a≥0,②3 a=4,且4≥a+3≥0,再解方程和不等式可得答案.
解:由题意得:①a+3=4,4≥3﹣a≥0,
解得:a=1,
②3﹣a=4,且4≥a+3≥0,
解得:a=﹣1,
故答案为:﹣1或1.
此题主要考查了多项式,关键是掌握多项式中次数最高的项的次数叫做多项式的次数.
41.-3
【解析】由是关于的二次二项式,可得且 再解方程,从而可得答案.
解: 是关于的二次二项式,
且
解得:
故答案为:
本题考查的是多项式的项与次数,掌握“利用多项式的项与次数的概念求解字母系数的值”是解本题的关键.
42.
【解析】直接利用多项式系数与次数确定方法得出 2m 1=0,进而得出答案.
解:∵关于x、y的多项式2x2+3mxy y2 xy 5是二次三项式,
∴3mxy xy=0,
则3m 1=0,
解得:m=.
故答案为:.
此题主要考查了多项式,正确掌握相关定义是解题关键.
43.2
【解析】根据多项式及其次数的定义,得|m|=2,2+m≠0.再根据绝对值的定义求出m.
解:由题意得:|m|=2,2+m≠0.
∴m=2.
故答案为:2.
本题主要考查多项式、绝对值,熟练掌握多项式、绝对值的定义是解决本题的关键.
44.45
【解析】观察不难发现,每一行的数字的个数为连续的奇数,且数字为相应的序数,然后求解即可.
解:∵每一行的数字的个数为连续的奇数,且数字为相应的序数,由图可知,前n行数的个数为1+3+5+…+2n-1==n2,
又∵452=2025,
∴表示2020的点在第45行.
故答案为:45.
本题是对数字变化规律的考查,观察出每一行的数字的个数为连续的奇数,且数字为相应的序数是解题的关键.
45.2
【解析】根据题意和表格中的已知数据,可以得出表格中的数据是以3、-5、2为一组循环出现,从而可用2022除以3,根据余数即可解答.
解:∵任意三个相邻格子中所填整数之和都相等,
∴3+a+b=a+b+c,
∴c=3,
∵a+b+c=b+c+(-5),
∴a=-5,
∴数据从左到右依次为3、-5、b、3、-5、b、……,
∴第9个数与第三个数相同,即b=2,
∴表格中的数据是从左到右以3、-5、2为一组依次循环出现,
∵2022÷3=674,
∴第2022个格子中的数为2,
故答案为:2.
本题考查数字类变化规律探究,理解题意,仔细观察,正确求出a、b、c的值,进而求得出数字的变化规律是解答的关键.
46..
【解析】观察图形可知每增加一个正方形地砖则增加两个等腰直角三角形,由此即可得到答案.
解:∵当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3),
∴观察可以发现每增加一个正方形地砖则增加两个等腰直角三角形,
∴一共有(为正整数)块正方形地砖,则等腰直角三角形地砖的块数为块,
故答案为:.
本题主要考查了图形类的规律问题,解题的关键在于能够根据图形找到规律.
47.(2n-1)(2n+1)=(2n)2-1
【解析】根据题目所给示例总结出相应的规律即可;
解:第1个等式,
第2个等式,
第3个等式,
第4个等式,
第n个等式(2n-1)(2n+1)=(2n)2-1;
故答案为:(2n-1)(2n+1)=(2n)2-1.
本题主要考查整式的应用,根据示例总结出相关规律是解题的关键.
48.2
【解析】根据第一次输出的结果是17,第二次输出的结果是52,…,总结出每次输出的结果的规律,求出2022次输出的结果是多少即可.
第一次输出的结果是:×34=17,
第二次输出的结果是:3×17+1=52,
第三次输出的结果是:×52=26,
第四次输出的结果是:×26=13,
第五次输出的结果是:3×13+1=40,
第六次输出的结果是:×40=20,
第七次输出的结果是:×20=10,
第八次输出的结果是:×10=5,
第九次输出的结果是:3×5+1=16,
第十次输出的结果是:×16=8,
第十一次输出的结果是:×8=4,
第十二次输出的结果是:×4=2,
第十三次输出的结果是:×2=1,
第十四次输出的结果是:3×1+1=4,
…,
∴从第十一次开始,输出的结果分别是4、2、1,…,不断循环出现,
∵(2022 10)÷3=2012÷3=670…2,
∴第2022次输出的结果是2.
故答案为:2.
此题主要考查了代数式求值问题,数字的变化规律,解答的关键是通过计算找到数字的变化规律.
49.10
【解析】分别求出每次变化后每组的人数,发现每五次循环一次,由此可知2022后与数完2的人数相同,即可求解.
解:编号分别是A、B、C、D、E,每组的人数分别是10、6、7、9、8,
数完1,编号分别是A、B、C、D、E,每组的人数分别是9、10、6、8、7,
数完2,编号分别是A、B、C、D、E,每组的人数分别是8、9、10、7、6,
数完3,编号分别是A、B、C、D、E,每组的人数分别是7、8、9、6、10,
数完4,编号分别是A、B、C、D、E,每组的人数分别是6、7、8、10、9,
数完5,编号分别是A、B、C、D、E,每组的人数分别是10、6、7、9、8,
……
∴每五次循环一次,
∵2022÷5=404…2,
∴2022后与数完2的人数相同,
∴C组有10人,
故答案为:10.
本题考查了数字的变化规律,根据题意,分别求出每次变化的人数,从而发现循环规律是解题的关键.
50.167288
【解析】根据前面三个等式,寻找规律解决问题.
解:由三个等式,得到规律:
=301545,可知:6×5 3×5 (6+3)×5,
=124254,可知:2×6 7×6 (2+7)×6,
=321244,可知:8×4 3×4 (8+3)×4,
∴=2×8 9×8 (2+9)×8=167288.
故答案为:167288.
本题考查数字的变化规律,能够根据所给的式子,探索出数字之间的联系是解题的关键.
51.12
【解析】由正方形分割制作可以知道,图2中阴影部分实际上是由图1中的等腰直角三角形A和平行四边形B组成,而图1中的A和B再加上C部分恰好是大正方形的四分之一,由此可解.
解:如下图所示,
图2中阴影部分实际上是由图1中的等腰直角三角形A和平行四边形B组成,
∵图1中的A、B、C三部分的面积等于==16
图1中的C的面积=
∴图2的阴影部分面积=图1中A和B的面积=16-4=12
故答案为:12.
本题考查了七巧板中的图形的构成和面积计算,熟悉七巧板中图形的分类是解题的关键.
52.443
【解析】先分别分析前三个图形小正方形的个数与排列的特点,再列出具有相同特点的表达式,从而可列出第20个图形的小正方形个数的表达式,从而可得答案.
解:由第1个图正方形的个数分别为6个、而
由第2个图正方形的个数分别为11个、而
由第3个图正方形的个数分别为18个、而
所以第20个图形正方形的个数为:
故答案为:
本题考查的是图形类的规律探究,掌握“从具体到一般的探究方法,再总结规律并利用规律解决问题”是解本题的关键.
53.179
【解析】根据已知图形得出第2个图形比第1个图形多:4﹣1=3个;第3个图形比第2个图形多:9﹣4=5个;第4个图形比第3个图形多:16﹣9=7个;即可得出后面一个图形比前面一个图形多的个数是连续奇数,进而得出公式第n个图形比第(n﹣1)个图形多2n﹣1个小正方形;由此利用规律得出答案即可.
解:根据分析可得出公式:第n个图形比第(n﹣1)个图形多2n﹣1个小正方形
∴第90个比第89个图形多2×90﹣1=179个小正方形
故答案为:179
此题主要考查了图形的变化规律,利用已知图形得出图形相邻之间的个数变化规律是解题关键.
54.
【解析】先将黄色部分向左平移,黄色部分减少的面积为绿色部分增加的面积,即可得出平移后黄色部分与绿色部分面积相等,设大正方形边长为b,红色部分边长为a,则黄色部分和绿色部分的长为a,宽为b-a,可得a2=20,a (b-a) =12,从而可得ab=32,则a2b2=322,即可求出b2
解∶如图,将黄色部分向左平移,
∴黄色部分减少的面积为绿色部分增加的面积,
∵红黄绿三块一样大的正方形,整个盒子为正方形,
∴平移后,黄色部分与绿色部分面积相等,
∴平移前,黄色的面积是13,绿色的面积是11,
∴平移后黄色部分与绿色部分面积为∶ ( 13+11) 2=12,
设大正方形边长为b,红色部分边长为a,则黄色部分和绿色部分的长为a,宽为b-a,
∴,
∴,
∴,
∴,
故答案为∶.
本题考查二元一次方程组的应用,正确平移图形,明确平移后黄色部分与绿色部分面积相等是解题的关键.
55.(1)
(2),证明见解析
(3)
【解析】(1)根据题目中式子的特点,可以写出第4个等式;
(2)根据题目中式子的特点,可以写出第个等式并加以证明;
(3)利用(2)进行求解即可.
(1)
解:∵①,
②,
③,
……
特点:等式左边是两个连续偶数的积加1,等式右边是两个连续偶数之间的奇数的平方,序号乘以2就是较小的偶数,
∴第4个等式是:.
故答案为:.
(2)
第个等式是:.
证明:∵左边,
右边,
∴左边=右边.
∴等式成立.
(3)
第个等式为:
即:.
故答案为:.
本题主要考查数字的变化规律,解答的关键是由所给的等式总结出存在的规律.
56.(1)4,7,10
(2)(3n+1)
【解析】(1)直接根据图形得出灰色水泥砖的块数即可;
(2)根据(1)中数据的个数得出变化规律为:3n+1,即可得出答案.
(1)
解:根据图形可得图①中有灰色水泥砖1+3=4块,
图②中有灰色水泥砖1+2×3=7块,
图③中有灰色水泥砖1+3×3=10块;
故答案为:4;7;10;
(2)
解:根据图形可得图①中有灰色水泥砖1+3=4块,
图②中有灰色水泥砖1+2×3=7块,
图③中有灰色水泥砖1+3×3=10块;
……
依次铺下去,
第n个图形中有灰色水泥砖(3n+1)块;
故答案为:(3n+1).
此题主要考查了图形的变化类,对于找规律的题目首先应找出发生变化的位置,并且观察变化规律.注意由特殊到一般的分析方法.
1.(2022·江苏无锡·七年级期末)下列说法错误的是( )
A.2x2-3xy-1是二次三项式 B.﹣x+1不是单项式
C.﹣的系数是﹣ D.﹣22xa3b2的次数是6
2.(2022·江苏盐城·七年级期末)如果整式是关于的二次三项式,那么等于( )
A.3 B.4 C.5 D.6
3.(2022·江苏南通·七年级期末)有18m长的木料,要做成一个如图的窗框.如果窗框横档的长度为xm,窗框厚度忽略不计,那么窗户的面积是( )
A. B. C. D.
4.(2022·江苏南通·七年级期末)某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )
A.万元 B.万元
C.万元 D.万元
5.(2022·江苏常州·七年级期末)甲、乙、丙三家超市同时为促销某种定价一样的相同商品,甲超市直接一次性降价30%,乙超市先降价20%,再降价10%:丙超市连续两次降价15%,那么顾客要买这件商品,到哪家超市购买更合算( )
A.甲 B.乙 C.丙 D.三家都一样
6.(2022·江苏无锡·七年级期末)今年苹果的单价比去年便宜了10%,已知今年苹果的单价是每千克a元,则去年苹果的单价是( )
A.10%a B. C. D.
7.(2022·江苏盐城·七年级期末)用代数式表示“的2倍与3的差”为( )
A. B. C. D.
8.(2022·江苏泰州·七年级期末)下列关于“代数式”的意义叙述正确的有( )个.
①x的4倍与y的2倍的和是;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元.
A.3 B.2 C.1 D.0
9.(2022·江苏南京·七年级期末)下列语句中,不正确的是( )
A.0是单项式 B.多项式的次数是4
C.的系数是 D.的系数和次数都是1
10.(2022·江苏宿迁·七年级期末)符号“”表示一种运算,运算规律如下:,,,,…,则( )
A. B. C. D.
11.(2022·江苏淮安·七年级期末)有一个正方体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的点数是( )
A.5 B.3 C.4 D.2
12.(2022·江苏盐城·七年级期末)如图所示的图形是由正方形和相同大小的圆按照一定规律摆放而成,按此规律,若要得到604个圆,则为第( )个图形.
A.200 B.201 C.202 D.302
13.(2022·江苏·苏州市振华中学校七年级期末)如图,甲、乙两动点分别从正方形的顶点、同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2000次相遇在边( )
A.上 B.上 C.上 D.上
14.(2022·江苏泰州·七年级期末)如图,、、三种不同型号的卡片,每种卡片各有9张,其中型卡片是边长为的正方形,型卡片是相邻两边长分别为、的长方形,型卡片是边长为的正方形(其中).从其中取张卡片(每种卡片至少取1张),并把取出的这些卡片拼成一个正方形,则所拼正方形的边长最大时,的最大值为( )
A.16 B.18 C.20 D.22
15.(2022·江苏淮安·七年级期末)如图,长方形ABCD是由30个大小相等的正方形拼成的,E、F、G、H分别在AD、 AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则长方形ABCD的面积是( )
A.2 B. C. D.
16.(2022·江苏南通·七年级期末)将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,…按此规律,若2022是第m行第n个数,则m,n的值分别是( )
A., B.,
C., D.,
17.(2022·江苏无锡·七年级期末)在一列数:a1,a2,a3,…,an中,a1=1,a2=2,a3=4,从第四个数开始,每一个数都等于它前三个数之积的个位数字,则这一列数中的第2022个数是( )
A.2 B.4 C.6 D.8
18.(2022·江苏南京·七年级期末)在某多媒体电子杂志的某一期上刊登了“正方形雪花图案的形成”的演示案例:作一个正方形,设每边长为4a,将每边四等分,作一凸一凹的两个边长为a的小正方形,得到图形如图(2)所示,称为第一次变化,再对图(2)的每个边做相同的变化,得到图形如图(3),称为第二次变化,如此连续作几次,便可得到一个绚丽多彩的雪花图案.如不断发展下去到第n次变化时,图形的面积和周长分别为( )
A.和 B.和 C.和 D.和
19.(2022·江苏盐城·七年级期末)把一个两位数交换十位数字和个位数字后得到一个新的两位数,若将这个新的两位数与原两位数相加,则所得的和一定是( )
A.11的倍数 B.奇数 C.偶数 D.9的倍数
20.(2022·江苏南通·七年级期末)一个两位数个位为a,十位数字为b,这个两位数为_____.
21.(2022·江苏淮安·七年级期末)的3倍与的差用代数式表示为______.
22.(2022·江苏南京·七年级期末)单项式的系数是______.
23.(2022·江苏扬州·七年级期末)单项式的系数是____.
24.(2022·江苏盐城·七年级期末)单项式﹣23xy3的次数是 _____.
25.(2022·江苏泰州·七年级期末)的系数是_______.
26.(2022·江苏常州·七年级期末)单项式-3的系数是_________.
27.(2022·江苏·射阳县第六中学七年级期末)单项式﹣2πa2bc的次数为 _____.
28.(2022·江苏盐城·七年级期末)单项式的系数为__________.
29.(2022·江苏无锡·七年级期末)写出一个含有字母a,b的三次单项式:________.
30.(2022·江苏南京·七年级期末)多项式a2b+2ab+b+1的次数是______.
31.(2022·江苏无锡·七年级期末)多项式2x2y﹣x3+5x2x2的次数是_____.
32.(2022·江苏·南京市第二十九中学七年级期末)多项式x3-4x2y3+26的次数是_______.
33.(2022·江苏·无锡市东林中学七年级期末)多项式2a2b-abc的次数是______.
34.(2022·江苏无锡·七年级期末)某校开展了丰富多彩的社团活动,每位学生可以选择自己最感兴趣的一个社团参加.已知参加体育类社团的有m人,参加文艺类社团的人数比参加体育类社团的人数多6人,参加科技类社团的人数比参加文艺类社团人数的多2人,则参加三类社团的总人数为_________(用m的代数式表示)
35.(2022·江苏常州·七年级期末)七巧板被西方人称为“东方魔术”,下面的两幅图是由同一个七巧板拼成的.已知七巧板拼成的正方形(如图1)边长为,则图2的“小狐狸”图案中阴影部分面积是____(用含的代数式表示).
36.(2022·江苏泰州·七年级期末)单项式的系数为______.
37.(2022·江苏宿迁·七年级期末)单项式﹣5xy2的次数是 _____.
38.(2022·江苏南京·七年级期末)写出一个系数为﹣5且含x,y的三次单项式_____.
39.(2022·江苏扬州·七年级期末)多项式的次数是_______.
40.(2022·江苏常州·七年级期末)若多项式3xa+3﹣x3﹣a+4是四次三项式,则a=____.
41.(2022·江苏扬州·七年级期末)若是关于的二次二项式,那么的值为______.
42.(2022·江苏南通·七年级期末)若关于、的多项式是二次三项式,则_______.
43.(2022·江苏江苏·七年级期末)若3x|m|﹣(2+m)x+5是关于x的二次三项式,那么m的值为 ___.
44.(2022·江苏扬州·七年级期末)如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右从小到大,且相邻两个点所表示的数相差1,每行数的和等于右边相应的数字.那么表示2022的点在第____行位置.
45.(2022·江苏盐城·七年级期末)如表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2022个格子中的数为________.
3 2 …
46.(2022·江苏扬州·七年级期末)某地铺设矩形人行道,由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3);以此类推.
现在街道上铺设一条这样的人行道,一共有(为正整数)块正方形地砖,则等腰直角三角形地砖的块数为_______(用含的代数式表示)
47.(2022·江苏扬州·七年级期末)观察:第1个等式,第2个等式,第3个等式,第4个等式…猜想:第n个等式是________.
48.(2022·江苏南京·七年级期末)有一数值转换器,原理如图所示,如果开始输入x的值是34,则第一次输出的结果是17,第二次输出的结果是52,……,那么第2022次输出的结果是_________.
49.(2022·江苏苏州·七年级期末)王老师在教学过程中善于把数学知识与实际生活联系在一起.在课堂上,他把全班同学分成五组,编号分别是A、B、C、D、E,每组的人数分别是10、6、7、9、8.游戏规则:当他数完1后,人数最少的那一组学生不动,其他各组各出一个人去人数最少的那组;当他数完2后,此时人数最少的那一组学生不动,其他各组再各出一个人去人数最少的那组;……如此进行下去,那么如果当王老师数完2022后,C组中的人数是_______.
50.(2022·江苏盐城·七年级期末)如图,“海春书局”把WIFI密码做成了数学题.小红在海春书局看书时,思索了一会儿,输入密码,顺利地连接到了“海春书局”的网络,那么她输入的密码是__________.
51.(2022·江苏连云港·七年级期末)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板,如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为8的正方形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为___________.
52.(2022·江苏泰州·七年级期末)在无限大的正方形网格中按规律涂成的阴影如图所示,第1、2、3个图中阴影部分小正方形的个数分别为6个、11个、18个,根据此规律,则第20个图中阴影部分小正方形的个数是__________.
53.(2022·江苏淮安·七年级期末)用同样大小的两种不同颜色的正方形纸片,按如图方式拼成正方形.第90个比第89个多___个小正方形纸片.
54.(2022·江苏南京·七年级期末)如图,红黄绿三块一样大的正方形纸片放在一个正方形盒内,它们之间互相重叠.已知露在外面的部分中,红色的面积是20,黄色的面积是13,绿色的面积是11,则正方形盒子的面积为_____________.
55.(2022·江苏镇江·七年级期末)观察下列式子:
①,
②,
③,
……
(1)根据你发现的规律,请写出第个等式________;
(2)根据你发现的规律,请写出第(为正整数)个等式________,并证明你所写出的等式的正确性;
(3)请写出第198个等式:_________.
56.(2022·江苏淮安·七年级期末)用正方形的白色水泥砖和灰色水泥砖按如图所示的方式铺人行道
(1)第①个图中有灰色水泥砖 块,
第②个图中有灰色水泥砖 块,
第③个图中有灰色水泥砖 块;
(2)依次铺下去,第n个图中有灰色水泥砖 块.
参考答案:
1.C
【解析】根据单项式的个数就是多项式的项数,如果一个多项式含有a个单项式,次数是b,那么这个多项式就叫b次a项式,再结合单项式的次数与系数确定方法,进而得出答案.
解:A、2x2-3xy-1是二次二项式,正确,故此选项不合题意;
B、-x+1不是单项式,正确,故此选项不合题意;
C、的系数是,原说法错误,故此选项符合题意;
D、22xa3b2的次数是6,正确,故此选项不合题意;
故选:C.
本题主要考查了多项式与单项式,正确掌握多项式的项数与次数确定方法是解题关键.
2.B
【解析】由于该多项式是关于x的二次三项式,可得n-2=2,即可求得n的值.
解:∵多项式是关于x的二次三项式,
∴n-2=2,
解得n=4,
故选:B.
本题考查了根据多项式的次数求参数的值,理解二次三项式的含义是解决本题的关键.
3.B
【解析】根据题意可知:用18m长的木料做成一个窗框,也就是它的周长是18m,已知窗框横档的长度为xm,那么窗框长为(18-3x)÷2=9-1.5x(m),根据长方形的面积=长×宽,把数据代入公式解答.
解:因为窗框横档的长度为xm,则显然窗框的长是(18-3x)÷2=9-1.5x(m),
∴窗户的面积是
故选:B
本题考查了列代数式,特别注意窗框的横档有3条边.解决问题的关键是读懂题意,找到所求的量的等量关系.
4.C
【解析】根据2月份比1月份减少了15%,可求出2月份的产值为a(1-15%),再由3月份比2月份增加了5%,列式即可得答案.
∵1月份产值为a万元,2月份比1月份减少了15%,
∴2月份的产值为a(1 15%),
∵3月份比2月份增加了5%,
∴3月份的产值为a(1-15%)(1+5%),
故选:C.
本题主要考查了列代数式,明确题意,用a表示出2月份、3月份的产值是解题的关键.
5.A
【解析】根据题意设商品的定价为,分别求得甲、乙、丙三家的售价,进而比较大小即可求解.
解:设商品的定价为,则甲超市的售价为:,
乙超市的售价为:
丙超市的售价为:
甲超市购买更合算
故选A
本题考查了列代数式,理解题意,列出代数式是解题的关键.
6.D
【解析】根据:去年的单价×(1-10%)=今年的单价,代入数据可求得去年的单价.
解:由题意得,去年的单价×(1-10%)=a,
则去年的单价=.
故选:D.
本题考查列代数式,关键是知道今年的单价和去年单价的关系,从而列出代数式.
7.B
【解析】先表示的2倍为,然后再减去3即可.
解:由题意得,的2倍与3的差表示为:.
故选:B.
本题考查了列代数式,解题的关键是正确理解文字语言中的关键词,比如该题中的“倍”、“差”等,从而明确其中的运算关系,正确列出代数式.
8.B
【解析】根据代数式的意义分别对三个叙述进行判断即可.
解:①x的4倍与y的2倍的和是,正确;
②小明以x米/分钟的速度跑了4分钟,再以y米/分钟的速度步行了2分钟,小明一共走了米,正确;
③苹果每千克x元,橘子每千克y元,买4千克橘子、2千克苹果一共花费元,错误;
故正确的有2个
故选:B.
此题考查了代数式的问题,解题的关键是掌握代数式的意义以及性质.
9.D
【解析】分别根据单独一个数也是单项式、多项式中每个单项式的最高次数是这个多项式的次数、单项式中的数字因数是这个单项式的系数、单项式中所有字母的指数和是这个单项式的次数解答即可.
解:A、0是单项式,正确,不符合题意;
B、多项式的次数是4,正确,不符合题意;
C、的系数是,正确,不符合题意;
D、的系数是-1,次数是1,错误,符合题意,
故选:D.
本题考查单项式、单项式的系数和次数、多项式的次数,理解相关知识的概念是解答的关键.
10.D
【解析】根据题意得到规律,从而得到,即可求解.
解:根据题意得:,
,
,
,
……,
由此发现,,
∴
.
故选:D
本题主要考查了数字类规律题,明确题意,准确得到规律是解题的关键.
11.B
【解析】观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,从而确定答案.
解:观察图形知道点数三和点数四相对,点数二和点数五相对且滚动四次一循环,
,
滚动第2022次后与第2次相同,
朝下的数字是4的对面3,
故选:B.
本题考查了正方体相对两个面上的文字及图形的变化类问题,解题的关键是发现规律.
12.B
【解析】观察图形的变化找到规律,再代入求解即可.
解:观察图形的变化可知.
第1个图形中圆的个数为4;
第2个图形中圆的个数为4+3=4+3×1=7;
第3个图形中圆的个数为4+3+3=4+3×2=10;
…
则第n个图形中圆的个数为4+3×(n﹣1)=3n+1.
当有604个圆时,得3n+1=604,
解得:n=201.
故选:B.
本题考查图形类规律,正确观察图形的变化是解题关键.
13.A
【解析】此题利用行程问题中的相遇问题,根据乙的速度是甲的速度的4倍,求得每一次相遇的地点,找出规律即可解答.
解:根据题意分析可得:乙的速度是甲的速度的4倍,故第1次相遇,甲走了正方形周长的 ;
从第2次相遇起,每次甲走了正方形周长的 ,
从第2次相遇起,5次一个循环.
因此可得:从开始出发起,每次相遇的位置依次是:AD,DC,点C,CB,BA;依次循环.
∵2000-1=1999,
1999÷5=399余4,
故它们第2000次相遇位置在边AB上.
故选:A.
本题主要考查了规律型的题目,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
14.C
【解析】根据题意每种卡片各有9张,每种至少取1张,拼成的正方形的边长要最大,则每种卡片应尽量多取,而全部用完时三种卡片的面积和为,则边长不是整数无法拼成.那么只需要面积比小,又是平方数即可,所以最大面积为,边长为10.
解:型卡片的面积为9b2,型卡片的面积为3b2,型卡片的面积为b2,
拼成的正方形的边长要最大,
拼成的正方形面积要最大,
,
,
当拼成的正方形面积为时最大,则边长为10,
此时:型9张,型6张,型1张,共16张;
型9张,型5张,型4张,共18张;
型9张,型4张,型7张,共20张;
故选:C.
本题主要考查了多项式乘多项式的运算方法,解题的关键是熟练掌握运算法则.
15.D
【解析】设每个小正方形的边形为,根据三角形的面积公式即可求出,的值,由此即可用含的代数式表示出四边形EFGH的面积,再根据四边形EFGH的面积为1即可求出,从而可得出结论.
解:设每个小正方形的边形为,
则:
,
∴四边形EFGH的面积=
∴
∴矩形ABCD的面积=
故选:D.
本题考查了矩形的性质、三角形的面积、矩形的面积以及利用平方根解一元二次方程,根据四边形EFGH的面积为1求出是解题的关键.
16.C
【解析】根据前4行归纳类推出每一行第1个数和最后一个数的一般规律,再结合每一行相邻两个数之差为1,由此即可得出答案.
解:由图可知,第1行第1个数为1,最后一个数为1,
第2行第1个数为2,最后一个数为,
第3行第1个数为3,最后一个数为,
第4行第1个数为4,最后一个数为,
归纳类推得:第行第1个数为,最后一个数为,
因为,
所以2022在第675行,即,
又因为第675行第1个数为675,且每一行相邻两个数之差为1,
所以,
故选:C.
本题考查了数字类规律探索,正确归纳类推出一般规律是解题关键.
17.D
【解析】可分别求出前12个数的情况,观察它是否具有周期性,再把2022代入求解即可.
解:依题意得:a1=1,a2=2,a3=4,
∵从第四个数开始,每一个数都等于它前三个数之积的个位数字,
∴1×2×4=8,即a4=8,
2×4×8=64,即a5=4,
4×8×4=128,即a6=8,
8×4×8=256,即a7=6,
4×8×6=192,即a8=2,
8×6×2=96,即a9=6,
6×2×6=72,即a10=2,
2×6×2=24,即a11=4,
6×2×4=48,即a12=8,
...,
即从第2个数开始,以2,4,8,4,8,6,2,6这8个数不断循环出现,
∵(2022-1)÷8=252......5,
∴第2022个数为8.
故选:D.
本题考查了找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.而具有周期性的题目,找出周期是解题的关键.
18.B
【解析】观察图形,发现对正方形每进行1次分形,周长增加1倍;每增加一个小正方形同时又减少一个相同的小正方形,即面积不变.
解:周长依次为32a,64a,128a,…,2n+4a,即无限增加,
所以不断发展下去到第n次变化时,图形的周长为2n+4a;
图形进行分形时,每增加一个小正方形同时又减少一个相同的小正方形,即面积不变,是一个定值16a2.
故选:B.
此题考查了图形的变化类,主要培养学生的观察能力和概括能力,观察出后一个图形的周长比它的前一个增加1倍是解题的关键,本题有一定难度.
19.A
【解析】用字母设出原两位数的十位数字和个位数字,表示出原两位数和新两位数的和,进行因式分解,看是哪个常数的倍数即可.
解:设原两位数十位上的数字是a,个位上的数字是b,则原两位数为10a+b,新两位数为10b+a,
∴这两个数的和为11a+11b=11(a+b),
∴所得的和一定是11的倍数,
故选:A.
本题考查了列代数式;注意两位数的表示方法为:10×十位数字+个位数字.
20.(10b+a)## (a+10b)
【解析】用十位上的数字乘以10,加上个位上的数字,即可列出这个两位数.
解:由题意得:这个两位数是:10b+a.
故答案为:(10b+a).
本题考查列代数式问题,解决本题的关键是根据各个数位上的数所表示的意义,能用字母表示一个数.
21.
【解析】根据题意,列出代数式,即可得到答案.
解:根据题意,得:;
故答案为:.
本题考查了列代数式,解题的关键是正确理解题意,列出代数式.
22.##0.5
【解析】根据单项式的系数的概念解答.
单项式的数字因数是
∴单项式的系数是.
故答案为:.
本题考查了单项式的系数的概念:单项式中的数字因数叫做单项式的系数.正确理解概念是解题的关键.
23.
【解析】单项式的系数就是所含字母前面的因数,由此即可求解.
解: 单项式的系数是.
故答案为:
本题考查单项式的系数的定义,解题关键是熟练掌握相关的定义即可求解.
24.
【解析】直接利用一个单项式中所有字母的指数的和叫做单项式的次数,进而得出答案.
解:单项式的次数是.
故答案为: .
本题主要考察单项式的概念,掌握单项式的概念是解题的关键.
25.
【解析】根据单项式的系数的定义进行解答即可.
解∶的系数是.
故答案为:.
本题考查的是单项式的系数,即单项式中的数字因数叫做单项式的系数.
26.
【解析】根据单项式中的数字因数是单项式的系数去确定,不要忽视数的符号.
∵单项式-3的系数是-3,
故答案为:-3.
本题考查了单项式的系数即单项式中的数字因数,准确理解定义是解题的关键.
27.4
【解析】根据单项式的次数的定义得出即可.
解:-2πa2bc单项式的次数是2+1+1=4,
故答案为:4.
本题考查了单项式的次数的定义,能熟记单项式的次数的定义的内容是解此题的关键,注意:单项式中的字母的指数的和,叫单项式的次数.
28.
【解析】根据单项式中的数字因数叫单项式的系数可得到答案
解:中的数字因数为
故答案为
本题考查了单项式的系数这个知识点,熟练掌握单项式系数概念是解题的关键.
29.(答案不唯一)
【解析】单项式中所有字母的指数和是单项式的次数,根据定义结合单项式含,从而可得答案.
解:含有字母a,b的三次单项式有:,
故答案为: (答案不唯一)
本题考查的是单项式的次数,掌握“单项式的次数”是解本题的关键.
30.3
【解析】分别求出多项式各项的次数,次数最高项的次数即为所求.
解:a2b+2ab+b+1各项次数分别为3、2、1、0,
故多项式的次数为3,
故答案为3.
本题考查多项式的次数,多项式中次数最高项的次数是多项式的次数.
31.4
【解析】根据多项式的次数是多项式中次数最高的单项的次数解答即可.
解:多项式2x2y﹣x3+5x2x2的次数是4次;
故答案为:4.
本题考查了多项式,利用了多项式的次数的定义是关键.确定多项式的次数,就是确定多项式中次数最高的项的次数.
32.5
【解析】根据多项式次数的定义解答.
解:多项式各项的次数分别为:3、5、0,
故答案为:5.
此题考查了多项式次数的定义:多项式中次数最高项的次数是多项式的次数,熟记定义是解题的关键.
33.3
【解析】利用几个单项式的和叫做多项式,每个单项式叫做多项式的项,多项式中次数最高的项的次数叫做多项式的次数,据此求解即可.
解:多项式2a2b-abc的次数是3.
故答案为:3.
本题主要考查了多项式,正确把握多项式的项数和次数确定方法是解题关键.
34.(m+11)
【解析】利用题干中的数量关系分别表示出参加文艺类社团的人数和参加科技类社团的人数,将参加三类社团的人数相加即可得出结论.
解:∵参加文艺类社团的人数比参加体育类社团的人数多6人,
∴参加文艺类社团的人数为:(m+6)人.
∵参加科技类社团的人数比参加文艺类社团人数的多2人,
∴参加科技类社团的人数为:(m+6)+2=(m+5)人.
∴参加三类社团的总人数为:m+(m+6)+(m+5)=(m+11)人.
故答案为:(m+11).
本题主要考查了列代数式,分别求出参加文艺类社团的人数和参加科技类社团的人数是解题的关键.
35.
【解析】由图可知,阴影部分面积为正方形面积的一半.
解:正方形的面积为,
∵阴影部分面积为正方形面积的一半
∴阴影部分面积为,
故答案为:.
本题主要列代数式,观察图形得出阴影部分为七巧板的右上部分是解题关键.
36.
【解析】根据单项式中的数字因数叫做单项式的系数求解.
单项式的系数为,
故答案为:.
本题考查了单项式:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式;单项式中的数字因数叫做单项式的系数,一个单项式中所有字母的指数的和叫做单项式的次数.
37.3
【解析】单项式中所有字母指数的和是单项式的次数,根据定义解答.
解:单项式﹣5xy2的次数是1+2=3,
故答案为:3.
此题考查了单项式的次数定义,熟记定义是解题的关键.
38.-5x2y(答案不唯一)
【解析】根据单项式的系数和次数的概念求解即可.
-5x2y是一个系数为﹣5且含x,y的三次单项式,故答案为-5x2y(答案不唯一).
本题考查单项式的概念,单项式中的数字因数叫做单项式的系数,单项式中所有字母的指数和叫做单项式的次数.
39.5
【解析】根据多项式的次数的定义分析即可,多项式的每一项都有次数,其中次数最高的项的次数,就是这个多项式的次数.
解:多项式的次数是的次数,是.
故答案为:5.
本题考查了多项式的次数,理解多项式的次数的定义是解题的关键.
40.﹣1或1##1或-1
【解析】根据题意可得:①a+3=4,4≥3 a≥0,②3 a=4,且4≥a+3≥0,再解方程和不等式可得答案.
解:由题意得:①a+3=4,4≥3﹣a≥0,
解得:a=1,
②3﹣a=4,且4≥a+3≥0,
解得:a=﹣1,
故答案为:﹣1或1.
此题主要考查了多项式,关键是掌握多项式中次数最高的项的次数叫做多项式的次数.
41.-3
【解析】由是关于的二次二项式,可得且 再解方程,从而可得答案.
解: 是关于的二次二项式,
且
解得:
故答案为:
本题考查的是多项式的项与次数,掌握“利用多项式的项与次数的概念求解字母系数的值”是解本题的关键.
42.
【解析】直接利用多项式系数与次数确定方法得出 2m 1=0,进而得出答案.
解:∵关于x、y的多项式2x2+3mxy y2 xy 5是二次三项式,
∴3mxy xy=0,
则3m 1=0,
解得:m=.
故答案为:.
此题主要考查了多项式,正确掌握相关定义是解题关键.
43.2
【解析】根据多项式及其次数的定义,得|m|=2,2+m≠0.再根据绝对值的定义求出m.
解:由题意得:|m|=2,2+m≠0.
∴m=2.
故答案为:2.
本题主要考查多项式、绝对值,熟练掌握多项式、绝对值的定义是解决本题的关键.
44.45
【解析】观察不难发现,每一行的数字的个数为连续的奇数,且数字为相应的序数,然后求解即可.
解:∵每一行的数字的个数为连续的奇数,且数字为相应的序数,由图可知,前n行数的个数为1+3+5+…+2n-1==n2,
又∵452=2025,
∴表示2020的点在第45行.
故答案为:45.
本题是对数字变化规律的考查,观察出每一行的数字的个数为连续的奇数,且数字为相应的序数是解题的关键.
45.2
【解析】根据题意和表格中的已知数据,可以得出表格中的数据是以3、-5、2为一组循环出现,从而可用2022除以3,根据余数即可解答.
解:∵任意三个相邻格子中所填整数之和都相等,
∴3+a+b=a+b+c,
∴c=3,
∵a+b+c=b+c+(-5),
∴a=-5,
∴数据从左到右依次为3、-5、b、3、-5、b、……,
∴第9个数与第三个数相同,即b=2,
∴表格中的数据是从左到右以3、-5、2为一组依次循环出现,
∵2022÷3=674,
∴第2022个格子中的数为2,
故答案为:2.
本题考查数字类变化规律探究,理解题意,仔细观察,正确求出a、b、c的值,进而求得出数字的变化规律是解答的关键.
46..
【解析】观察图形可知每增加一个正方形地砖则增加两个等腰直角三角形,由此即可得到答案.
解:∵当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3),
∴观察可以发现每增加一个正方形地砖则增加两个等腰直角三角形,
∴一共有(为正整数)块正方形地砖,则等腰直角三角形地砖的块数为块,
故答案为:.
本题主要考查了图形类的规律问题,解题的关键在于能够根据图形找到规律.
47.(2n-1)(2n+1)=(2n)2-1
【解析】根据题目所给示例总结出相应的规律即可;
解:第1个等式,
第2个等式,
第3个等式,
第4个等式,
第n个等式(2n-1)(2n+1)=(2n)2-1;
故答案为:(2n-1)(2n+1)=(2n)2-1.
本题主要考查整式的应用,根据示例总结出相关规律是解题的关键.
48.2
【解析】根据第一次输出的结果是17,第二次输出的结果是52,…,总结出每次输出的结果的规律,求出2022次输出的结果是多少即可.
第一次输出的结果是:×34=17,
第二次输出的结果是:3×17+1=52,
第三次输出的结果是:×52=26,
第四次输出的结果是:×26=13,
第五次输出的结果是:3×13+1=40,
第六次输出的结果是:×40=20,
第七次输出的结果是:×20=10,
第八次输出的结果是:×10=5,
第九次输出的结果是:3×5+1=16,
第十次输出的结果是:×16=8,
第十一次输出的结果是:×8=4,
第十二次输出的结果是:×4=2,
第十三次输出的结果是:×2=1,
第十四次输出的结果是:3×1+1=4,
…,
∴从第十一次开始,输出的结果分别是4、2、1,…,不断循环出现,
∵(2022 10)÷3=2012÷3=670…2,
∴第2022次输出的结果是2.
故答案为:2.
此题主要考查了代数式求值问题,数字的变化规律,解答的关键是通过计算找到数字的变化规律.
49.10
【解析】分别求出每次变化后每组的人数,发现每五次循环一次,由此可知2022后与数完2的人数相同,即可求解.
解:编号分别是A、B、C、D、E,每组的人数分别是10、6、7、9、8,
数完1,编号分别是A、B、C、D、E,每组的人数分别是9、10、6、8、7,
数完2,编号分别是A、B、C、D、E,每组的人数分别是8、9、10、7、6,
数完3,编号分别是A、B、C、D、E,每组的人数分别是7、8、9、6、10,
数完4,编号分别是A、B、C、D、E,每组的人数分别是6、7、8、10、9,
数完5,编号分别是A、B、C、D、E,每组的人数分别是10、6、7、9、8,
……
∴每五次循环一次,
∵2022÷5=404…2,
∴2022后与数完2的人数相同,
∴C组有10人,
故答案为:10.
本题考查了数字的变化规律,根据题意,分别求出每次变化的人数,从而发现循环规律是解题的关键.
50.167288
【解析】根据前面三个等式,寻找规律解决问题.
解:由三个等式,得到规律:
=301545,可知:6×5 3×5 (6+3)×5,
=124254,可知:2×6 7×6 (2+7)×6,
=321244,可知:8×4 3×4 (8+3)×4,
∴=2×8 9×8 (2+9)×8=167288.
故答案为:167288.
本题考查数字的变化规律,能够根据所给的式子,探索出数字之间的联系是解题的关键.
51.12
【解析】由正方形分割制作可以知道,图2中阴影部分实际上是由图1中的等腰直角三角形A和平行四边形B组成,而图1中的A和B再加上C部分恰好是大正方形的四分之一,由此可解.
解:如下图所示,
图2中阴影部分实际上是由图1中的等腰直角三角形A和平行四边形B组成,
∵图1中的A、B、C三部分的面积等于==16
图1中的C的面积=
∴图2的阴影部分面积=图1中A和B的面积=16-4=12
故答案为:12.
本题考查了七巧板中的图形的构成和面积计算,熟悉七巧板中图形的分类是解题的关键.
52.443
【解析】先分别分析前三个图形小正方形的个数与排列的特点,再列出具有相同特点的表达式,从而可列出第20个图形的小正方形个数的表达式,从而可得答案.
解:由第1个图正方形的个数分别为6个、而
由第2个图正方形的个数分别为11个、而
由第3个图正方形的个数分别为18个、而
所以第20个图形正方形的个数为:
故答案为:
本题考查的是图形类的规律探究,掌握“从具体到一般的探究方法,再总结规律并利用规律解决问题”是解本题的关键.
53.179
【解析】根据已知图形得出第2个图形比第1个图形多:4﹣1=3个;第3个图形比第2个图形多:9﹣4=5个;第4个图形比第3个图形多:16﹣9=7个;即可得出后面一个图形比前面一个图形多的个数是连续奇数,进而得出公式第n个图形比第(n﹣1)个图形多2n﹣1个小正方形;由此利用规律得出答案即可.
解:根据分析可得出公式:第n个图形比第(n﹣1)个图形多2n﹣1个小正方形
∴第90个比第89个图形多2×90﹣1=179个小正方形
故答案为:179
此题主要考查了图形的变化规律,利用已知图形得出图形相邻之间的个数变化规律是解题关键.
54.
【解析】先将黄色部分向左平移,黄色部分减少的面积为绿色部分增加的面积,即可得出平移后黄色部分与绿色部分面积相等,设大正方形边长为b,红色部分边长为a,则黄色部分和绿色部分的长为a,宽为b-a,可得a2=20,a (b-a) =12,从而可得ab=32,则a2b2=322,即可求出b2
解∶如图,将黄色部分向左平移,
∴黄色部分减少的面积为绿色部分增加的面积,
∵红黄绿三块一样大的正方形,整个盒子为正方形,
∴平移后,黄色部分与绿色部分面积相等,
∴平移前,黄色的面积是13,绿色的面积是11,
∴平移后黄色部分与绿色部分面积为∶ ( 13+11) 2=12,
设大正方形边长为b,红色部分边长为a,则黄色部分和绿色部分的长为a,宽为b-a,
∴,
∴,
∴,
∴,
故答案为∶.
本题考查二元一次方程组的应用,正确平移图形,明确平移后黄色部分与绿色部分面积相等是解题的关键.
55.(1)
(2),证明见解析
(3)
【解析】(1)根据题目中式子的特点,可以写出第4个等式;
(2)根据题目中式子的特点,可以写出第个等式并加以证明;
(3)利用(2)进行求解即可.
(1)
解:∵①,
②,
③,
……
特点:等式左边是两个连续偶数的积加1,等式右边是两个连续偶数之间的奇数的平方,序号乘以2就是较小的偶数,
∴第4个等式是:.
故答案为:.
(2)
第个等式是:.
证明:∵左边,
右边,
∴左边=右边.
∴等式成立.
(3)
第个等式为:
即:.
故答案为:.
本题主要考查数字的变化规律,解答的关键是由所给的等式总结出存在的规律.
56.(1)4,7,10
(2)(3n+1)
【解析】(1)直接根据图形得出灰色水泥砖的块数即可;
(2)根据(1)中数据的个数得出变化规律为:3n+1,即可得出答案.
(1)
解:根据图形可得图①中有灰色水泥砖1+3=4块,
图②中有灰色水泥砖1+2×3=7块,
图③中有灰色水泥砖1+3×3=10块;
故答案为:4;7;10;
(2)
解:根据图形可得图①中有灰色水泥砖1+3=4块,
图②中有灰色水泥砖1+2×3=7块,
图③中有灰色水泥砖1+3×3=10块;
……
依次铺下去,
第n个图形中有灰色水泥砖(3n+1)块;
故答案为:(3n+1).
此题主要考查了图形的变化类,对于找规律的题目首先应找出发生变化的位置,并且观察变化规律.注意由特殊到一般的分析方法.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
