8年级上册数学人教版课时练《13.3.2 等边三角形》(word、含答案)
文档属性
| 名称 | 8年级上册数学人教版课时练《13.3.2 等边三角形》(word、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 21:42:31 | ||
图片预览

文档简介
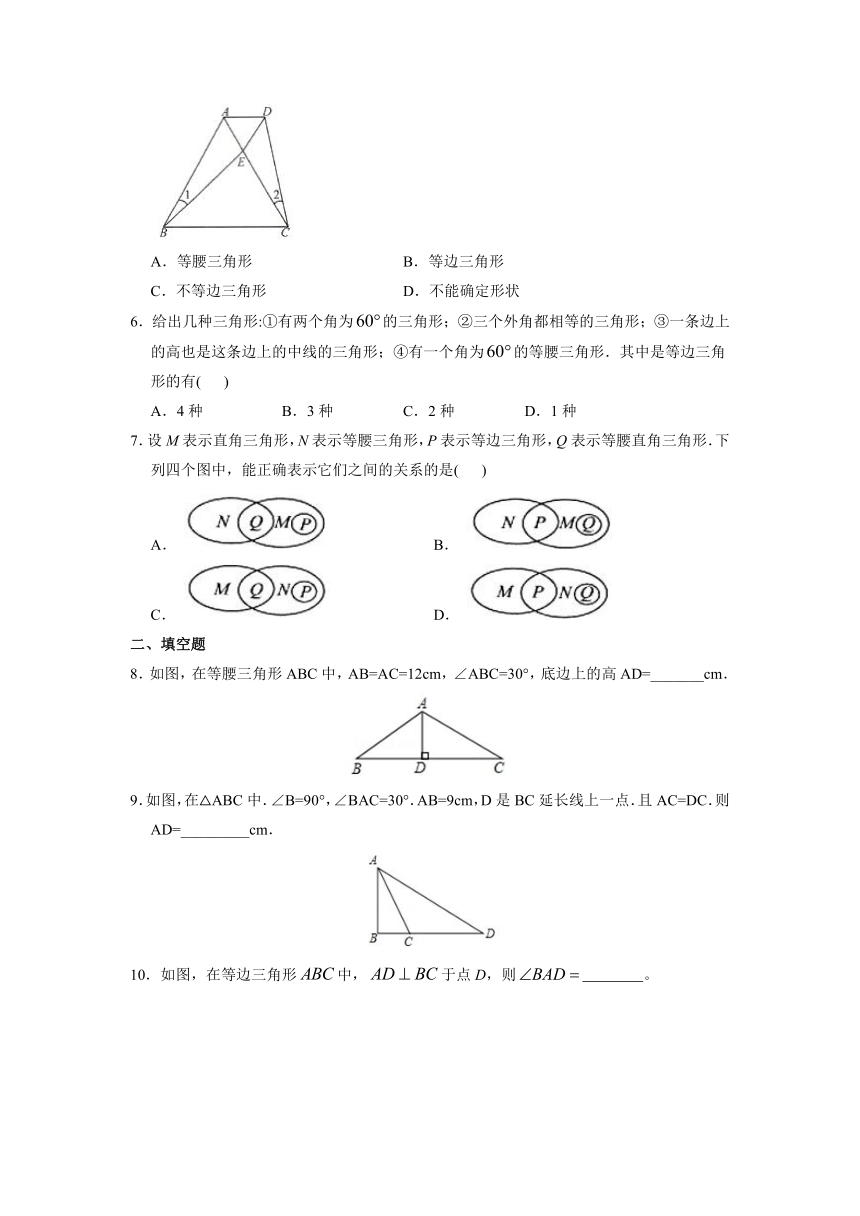
《13.3.2 等边三角形》课时练
一、选择题
1.如图,等边三角形中,,垂足为D,点E在线段上,,则等于( )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC长为( )
A.4cm B.2cm C.1cm D.m
3.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=10m,∠A=30°,则立柱BC的长度是( )
A. 5m B. 8m C. 10m D. 20m
4.如图,已知∠ABC=60°,DA是BC的垂直平分线,BE平分∠ABD交AD于点E,连接CE.则下列结论:①BE=AE;②BD=AE;③AE=2DE;④S△ABE=S△CBE,其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
5.如图,E是等边中边上的点,,则对的形状判断最准确的是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
6.给出几种三角形:①有两个角为的三角形;②三个外角都相等的三角形;③一条边上的高也是这条边上的中线的三角形;④有一个角为的等腰三角形.其中是等边三角形的有( )
A.4种 B.3种 C.2种 D.1种
7.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间的关系的是( )
A. B.
C. D.
二、填空题
8.如图,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,底边上的高AD=_______cm.
9.如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则AD=_________cm.
10.如图,在等边三角形中,于点D,则 。
11.如图是屋顶的“人”字形钢架,其中斜梁,顶角,跨度,为中柱(即底边的中线),两根支撑架,则 .
三、简答题
12.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD=DC.
13.如图,△ABC中,∠ACB=90°,CD是△ABC的高,∠A=30°,AB=4,求BD长.
参考答案
题号 1 2 3 4 5 6 7
答案 A C A C B B C
8.6
18
10.30
11.5
12.解:如图,连接DB.
∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠ABD,
∵BA=BC,∠B=120°,
∴∠A=∠C=(180°﹣120°)=30°,
∴∠ABD=30°,
又∵∠ABC=120°,
∴∠DBC=120°﹣30°=90°,
∴BD=DC,
∴AD=DC.
13.解:∵△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=×4=2,
∵CD是△ABC的高,
∴∠CDA=∠ACB=90°,
∠B=∠B,
故∠BCD=∠A=30°,
∴在Rt△BCD中,BD=BC=×2=1,
∴BD=1.
一、选择题
1.如图,等边三角形中,,垂足为D,点E在线段上,,则等于( )
A. B. C. D.
2.在Rt△ABC中,∠C=90°,∠B=30°,斜边AB的长为2cm,则AC长为( )
A.4cm B.2cm C.1cm D.m
3.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=10m,∠A=30°,则立柱BC的长度是( )
A. 5m B. 8m C. 10m D. 20m
4.如图,已知∠ABC=60°,DA是BC的垂直平分线,BE平分∠ABD交AD于点E,连接CE.则下列结论:①BE=AE;②BD=AE;③AE=2DE;④S△ABE=S△CBE,其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
5.如图,E是等边中边上的点,,则对的形状判断最准确的是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定形状
6.给出几种三角形:①有两个角为的三角形;②三个外角都相等的三角形;③一条边上的高也是这条边上的中线的三角形;④有一个角为的等腰三角形.其中是等边三角形的有( )
A.4种 B.3种 C.2种 D.1种
7.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间的关系的是( )
A. B.
C. D.
二、填空题
8.如图,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,底边上的高AD=_______cm.
9.如图,在△ABC中.∠B=90°,∠BAC=30°.AB=9cm,D是BC延长线上一点.且AC=DC.则AD=_________cm.
10.如图,在等边三角形中,于点D,则 。
11.如图是屋顶的“人”字形钢架,其中斜梁,顶角,跨度,为中柱(即底边的中线),两根支撑架,则 .
三、简答题
12.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD=DC.
13.如图,△ABC中,∠ACB=90°,CD是△ABC的高,∠A=30°,AB=4,求BD长.
参考答案
题号 1 2 3 4 5 6 7
答案 A C A C B B C
8.6
18
10.30
11.5
12.解:如图,连接DB.
∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠ABD,
∵BA=BC,∠B=120°,
∴∠A=∠C=(180°﹣120°)=30°,
∴∠ABD=30°,
又∵∠ABC=120°,
∴∠DBC=120°﹣30°=90°,
∴BD=DC,
∴AD=DC.
13.解:∵△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=×4=2,
∵CD是△ABC的高,
∴∠CDA=∠ACB=90°,
∠B=∠B,
故∠BCD=∠A=30°,
∴在Rt△BCD中,BD=BC=×2=1,
∴BD=1.
