第四章 几何图形初步(原卷版+解析版)【高效培优】2022-2023学年七年级数学上册必考重难点突破必刷卷(人教版)
文档属性
| 名称 | 第四章 几何图形初步(原卷版+解析版)【高效培优】2022-2023学年七年级数学上册必考重难点突破必刷卷(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 10:26:09 | ||
图片预览




文档简介
第四章几何图形初步
一、单选题
1.下列说法不正确的是( )
A.两点确定一条直线
B.两点间线段最短
C.两点间的线段叫做两点间的距离
D.正多边形的各边相等,各角相等
2.图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体可能是( )
A. B. C. D.
3.下列图形中,是长方体的平面展开图的是( )
A. B.
C. D.
4.粉刷墙壁时,粉刷工人用滚筒在墙上刷过几次后,墙壁马上换上了“新装”,在这个过程中,你认为下列判断正确的是( )
A.点动成线 B.线动成面 C.面动成体 D.面与面相交得到线
5.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4 B.3 C.2 D.1
6.如图,BC=,D为AC的中点,DC=3cm,则AB的长是( )
A.cm B.4cm C.cm D.5cm
7.若,则的补角是( )
A. B. C. D.
8.下面几何体中,是圆锥的为( )
A. B. C. D.
9.若一个棱柱有7个面,则它是( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
10.如图,该几何体的截面形状是( )
A.三角形 B.长方形 C.圆形 D.五边形
二、填空题
11.将两个三角尺的直角顶点重合为如图所示的位置,若,则_________.
12.的补角等于______________________′.
13.若一个角的余角为35°,则它的补角度数为 ______.
14.如图,在的同侧,,点为的中点,若,则的最大值是_____.
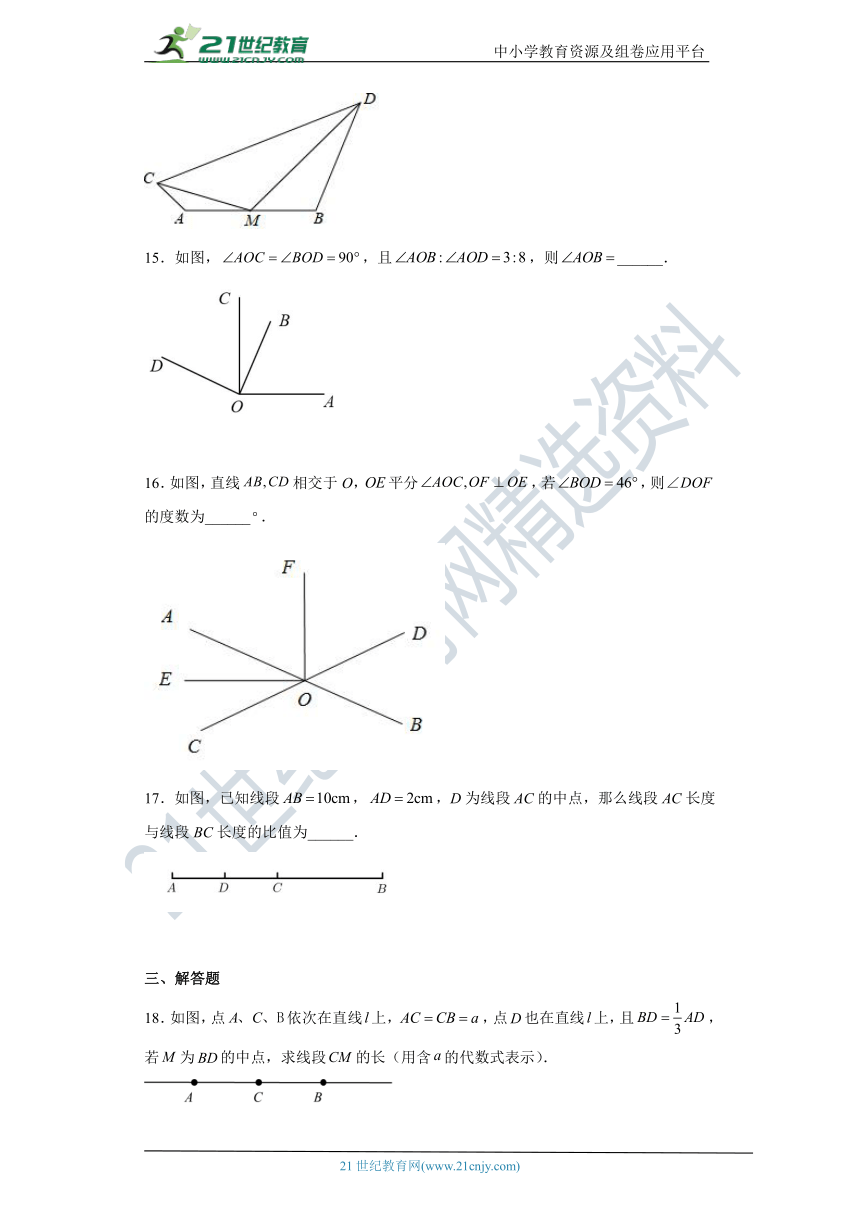
15.如图,,且,则______.
16.如图,直线相交于O,平分,若,则的度数为______.
17.如图,已知线段,,D为线段AC的中点,那么线段AC长度与线段BC长度的比值为______.
三、解答题
18.如图,点依次在直线上,,点也在直线上,且,若为的中点,求线段的长(用含的代数式表示).
19.如图,C为线段AD上一点,点B为CD的中点,且cm,cm.
(1)图中共有______条线段?
(2)求AC的长;
(3)若点E在直线AD上,且cm,求BE的长.
20.如图①,已知线段AB=12 cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点.
(1)若点C恰好是AB中点,则DE=_____cm.
(2)若AC=4 cm,求DE的长;
(3)试利用“字母代替数”的方法,说明不论AC取何值(不超过12 cm),DE的长不变;
(4)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.
21.已知OD、OE分别是∠AOB、∠AOC的角平分线.
(1)如图1,OC是∠AOB外部的一条射线.
①若∠AOC=32°,∠BOC=126°,则∠DOE= °;
②若∠BOC=164°,求∠DOE的度数;
(2)如图2,OC是∠AOB内部的一条射线,∠BOC=n°,用n的代数式表示∠DOE的度数.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】分别利用直线的性质,线段的性质,正多边形的性质以及两点间的距离的定义分析求出即可.
【详解】解:A. 两点确定一条直线是正确的,不符合题意;
B. 两点间线段最短是正确的,不符合题意;
C. 两点间的垂线段的长度叫做两点间的距离,原来的说法错误,符合题意;
D.正多边形的各边相等,各角相等是正确的,不符合题意.
故选:C.
【点睛】此题主要考查了直线的性质,线段的性质,正多边形的性质以及两点间的距离等知识,正确把握相关性质是解题关键.
2.B
【分析】观察长方体,可知第一部分所对应的几何体在长方体中,上面有二个正方体,下面有二个正方体,再在BC选项中根据图形作出判断.
【详解】解:由长方体和第一部分所对应的几何体可知,
第一部分所对应的几何体上面有二个正方体,下面有二个正方体,并且与选项B相符.
故选:B.
【点睛】本题考查了认识立体图形,找到长方体中,第一部分所对应的几何体的形状是解题的关键.
3.B
【分析】根据长方体有六个面,展开后长方体相对的两个面不可能相邻进行判断.
【详解】A.中间两个细长方形相邻,错误;
B.各个相对的面没有相邻,正确;
C.中间两个大长方形相邻,错误;
D.图中有七个面,错误;
故选 B.
【点睛】本题考查几何体的展开,关键在于理解长方体有六个面,展开后长方体相对的两个面不可能相邻.
4.B
【分析】点动线,线动成面,将滚筒看做线,在运动过程中形成面.
【详解】解:滚筒看成是线,滚动的过程成形成面,
故选:B.
【点睛】本题考查点、线、面的关系;理解点动成线,线动成面的过程是解题的关键.
5.C
【分析】由AB=10cm,BC=4cm.于是得到AC=AB+BC=14cm,根据线段中点的定义由D是AC的中点,得到AD,根据线段的和差得到MD=AD﹣AM,于是得到结论.
【详解】解:∵AB=10cm,BC=4cm,
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
【点睛】此题主要考查了两点之间的距离,线段的和差、线段的中点的定义,利用线段差及中点性质是解题的关键.
6.B
【分析】先根据已知等式得出AB与AC的等量关系,再根据线段的中点定义可得出AC的长,从而可得出答案.
【详解】∵
∴,即
∵D为AC的中点,
∴
∴
故选:B.
【点睛】本题考查了线段的和差倍分、线段的中点定义,掌握线段的中点定义是解题关键.
7.C
【分析】根据补角的定义,即若两个角的和等于 ,就称这两个角互补,即可解答.
【详解】解:∵,
∴的补角等于 ,
故选:C
【点睛】本题主要考查了补角的定义,解题的关键是熟练掌握若两个角的和等于 ,就称这两个角互补.
8.B
【分析】观察所给几何体,可以直接得出答案.
【详解】解:A选项为圆柱,不合题意;
B选项为圆锥,符合题意;
C选项为三棱柱,不合题意;
D选项为球,不合题意;
故选B.
【点睛】本题考查常见几何体的识别,熟练掌握常见几何体的特征是解题的关键.圆锥面和一个截它的平面,组成的空间几何图形叫圆锥.
9.C
【分析】根据棱柱有两个底面求出侧面数,即可选择.
【详解】棱柱必有两个底面,则剩下7-2=5个面是侧面,所以为五棱柱.
故选C
【点睛】本题考查认识立体图形棱柱,解题的关键是知道棱柱必有两个底面.
10.B
【分析】根据几何体的形状是长方体,进行如图截面即可判断形状.
【详解】解:根据题意得:该几何体的截面形状是长方形.
故选:B
【点睛】本题考查了截一个几何体的应用,目的是培养学生的空间想象能力和动手操作能力.
11.
【分析】由∠AOB=∠COD=90°,∠AOC=∠BOD,进而∠AOC=∠BOD=108°-90°=18°,由此能求出∠BOC.
【详解】解: ∠AOB=∠COD=90°,
∠AOC=∠BOD, 又∠AOD=108°,
∠AOC=∠BOD=108°-90°=18°,
∠BOC=90°-18°=72°.
故答案为:.
【点睛】本题考查的是角的和差,两锐角的互余,掌握以上知识是解题的关键.
12. 143 45
【分析】根据补角定义直接解答.
【详解】的补角等于:180° =143°45′.
故答案为:143;45.
【点睛】此题属于基础题,较简单,本题考查补角的概念,解决本题的关键是熟记补角的概念.
13.125°##125度
【分析】若两个角的和为 则这两个角互余,若两个角的和为 则这两个角互补,根据定义直接可得答案.
【详解】解: 一个角的余角为35°,
这个角为:
则它的补角度数为:
故答案为:
【点睛】本题考查的是余角与补角的计算,掌握“余角与补角的含义”是解本题的关键.
14.14
【分析】如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,证明△A′MB′为等边三角形,即可解决问题.
【详解】解:如图,作点关于的对称点,点关于的对称点.
,
,
,
,
,
为等边三角形
,
的最大值为,
故答案为.
【点睛】本题考查等边三角形的判定和性质,两点之间线段最短,解题的关键是学会添加常用辅助线,学会利用两点之间线段最短解决最值问题
15.54°##54度
【分析】,通过,利用表示出,再根据角与角之间的关系,得到关于的方程,求解方程,即可得出答案.
【详解】解:设,
,
,
,
,解得:,
故答案为:.
【点睛】本题主要是考查了角的求解,熟练利用角与角之间的关系,求出未知角读书,这是解决本题的关键.
16.67
【分析】根据角平分线与角度的运算即可求解.
【详解】∵,
∴,
∵平分,
∴,
又∵,
∴,
∵,
∴
.
故答案为:67.
【点睛】此题主要考查角平分线的性质,解题的关键是熟知角度计算.
17.
【分析】根据为线段的中点,可得,即可求解.
【详解】D为AC的中点,
,
,
∵,
,
,
故答案为:.
【点睛】本题主要考查了与线段中点有关的计算,求比值,解题的关键在于能够根据题意求出.
18.a或a
【分析】分A、B在点D同侧,A、B在点D两侧,两种情况分别求解.
【详解】解:当A、B在点D同侧时,
∵AC=CB=a,BD=AD,
∴AD=3BD=3a,
∵M是BD中点,
∴BM=DM=a,
∴CM=BC+BM=a;
当A、B在点D两侧时,
∵AC=CB=a,BD=AD,
∴AB=2a,AD=a,BD=a,
∵M为BD中点,
∴DM=BM=BD=a,
∴CM=AB-AC-BM=a.
【点睛】本题考查了两点间的距离,中点的性质,解题的关键是灵活运用线段的和差,要分类讨论,以防遗漏.
19.(1)6;(2)5cm;(3)4cm或10cm.
【分析】(1)固定A为端点,数线段,依次类推,最后求和即可;
(2)根据AC=AD-CD=AC-2BC,计算即可;
(3)分点E在点A左边和右边两种情形求解.
【详解】(1)以A为端点的线段为:AC,AB,AD;以C为端点的线段为:CB,CD;
以B为端点的线段为:BD;
共有3+2+1=6(条);
故答案为:6.
(2)解:∵B为CD中点,cm
∴cm
∵cm
∴cm
(3)cm,cm
第一种情况:点E在线段AD上(点E在点A右侧).
cm
第二种情况:点E在线段DA延长线上(点E在点A左侧).
cm.
【点睛】本题考查了数线段,线段的中点,线段的和(差),熟练掌握线段的中点,灵活运用线段的和,差是解题的关键.
20.(1)DE=6cm,(2)DE=6cm,(3)见解析(4)见解析
【分析】(1)由AB=12cm,点D、E分别是AC和BC的中点,即可推出DE=(AC+BC)=AB=6cm,
(2)由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC=2cm,BE=EC=4cm,即可推出DE的长度,
(3)设AC=acm,然后通过点D、E分别是AC和BC的中点,即可推出DE=(AC+BC)=AB=cm,即可推出结论,
(4)由若OD、OE分别平分∠AOC和∠BOC,即可推出∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=60°,即可推出∠DOE的度数与射线OC的位置无关.
【详解】(1)∵AB=12cm,点D、E分别是AC和BC的中点,C点为AB的中点,
∴AC=BC=6cm,
∴CD=CE=3cm,
∴DE=6cm,
(2)∵AB=12cm,
∴AC=4cm,
∴BC=8cm,
∵点D、E分别是AC和BC的中点,
∴CD=2cm,CE=4cm,
∴DE=6cm,
(3)设AC=acm,
∵点D、E分别是AC和BC的中点,
∴DE=CD+CE=(AC+BC)=AB=6cm,
∴不论AC取何值(不超过12cm),DE的长不变,
(4)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB,
∵∠AOB=120°,
∴∠DOE=60°,
∴∠DOE的度数与射线OC的位置无关.
【点睛】本题主要考查角平分线和线段的中点的性质,关键在于认真的进行计算,熟练运用相关的性质定理.
21.(1)63;(2)∠DOE=82°;(3)∠DOE=n°
【分析】(1)根据角平分线的定义,和角的和差关系,可找到∠BOC和∠DOE的度数,代入数据即可;
(2)根据角平分线的定义,和角的和差关系,可找到∠BOC和∠DOE的度数,代入数据即可.
【详解】解:(1)∵OD、OE分别是∠AOB、∠AOC,
∴∠AOD=∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD+∠AOE=(∠AOB+∠AOC)=∠BOC,
∵∠BOC=126°
,∴∠DOE=63°,
故答案为:63.
(2)由①可知,∠DOE=∠BOC,
∵∠∠BOC=164°,
∴∠DOE=82°.
(3)∵OD、OE分别是∠AOB、∠AOC,
∴∠AOD=∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD﹣∠AOE=(∠AOB﹣∠AOC)=∠BOC,
∵∠BOC=n°,
∴∠DOE=n°.
【点睛】本题主要考查角平分线的定义,角的和差计算,根据图形,找到角之间的关系,是解题关键.
答案第1页,共2页
一、单选题
1.下列说法不正确的是( )
A.两点确定一条直线
B.两点间线段最短
C.两点间的线段叫做两点间的距离
D.正多边形的各边相等,各角相等
2.图中的长方体是由三个部分拼接而成的,每一部分都是由四个同样大小的小正方体组成的,那么其中第一部分所对应的几何体可能是( )
A. B. C. D.
3.下列图形中,是长方体的平面展开图的是( )
A. B.
C. D.
4.粉刷墙壁时,粉刷工人用滚筒在墙上刷过几次后,墙壁马上换上了“新装”,在这个过程中,你认为下列判断正确的是( )
A.点动成线 B.线动成面 C.面动成体 D.面与面相交得到线
5.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4 B.3 C.2 D.1
6.如图,BC=,D为AC的中点,DC=3cm,则AB的长是( )
A.cm B.4cm C.cm D.5cm
7.若,则的补角是( )
A. B. C. D.
8.下面几何体中,是圆锥的为( )
A. B. C. D.
9.若一个棱柱有7个面,则它是( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
10.如图,该几何体的截面形状是( )
A.三角形 B.长方形 C.圆形 D.五边形
二、填空题
11.将两个三角尺的直角顶点重合为如图所示的位置,若,则_________.
12.的补角等于______________________′.
13.若一个角的余角为35°,则它的补角度数为 ______.
14.如图,在的同侧,,点为的中点,若,则的最大值是_____.
15.如图,,且,则______.
16.如图,直线相交于O,平分,若,则的度数为______.
17.如图,已知线段,,D为线段AC的中点,那么线段AC长度与线段BC长度的比值为______.
三、解答题
18.如图,点依次在直线上,,点也在直线上,且,若为的中点,求线段的长(用含的代数式表示).
19.如图,C为线段AD上一点,点B为CD的中点,且cm,cm.
(1)图中共有______条线段?
(2)求AC的长;
(3)若点E在直线AD上,且cm,求BE的长.
20.如图①,已知线段AB=12 cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点.
(1)若点C恰好是AB中点,则DE=_____cm.
(2)若AC=4 cm,求DE的长;
(3)试利用“字母代替数”的方法,说明不论AC取何值(不超过12 cm),DE的长不变;
(4)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD,OE分别平分∠AOC和∠BOC,试说明∠DOE=60°与射线OC的位置无关.
21.已知OD、OE分别是∠AOB、∠AOC的角平分线.
(1)如图1,OC是∠AOB外部的一条射线.
①若∠AOC=32°,∠BOC=126°,则∠DOE= °;
②若∠BOC=164°,求∠DOE的度数;
(2)如图2,OC是∠AOB内部的一条射线,∠BOC=n°,用n的代数式表示∠DOE的度数.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】分别利用直线的性质,线段的性质,正多边形的性质以及两点间的距离的定义分析求出即可.
【详解】解:A. 两点确定一条直线是正确的,不符合题意;
B. 两点间线段最短是正确的,不符合题意;
C. 两点间的垂线段的长度叫做两点间的距离,原来的说法错误,符合题意;
D.正多边形的各边相等,各角相等是正确的,不符合题意.
故选:C.
【点睛】此题主要考查了直线的性质,线段的性质,正多边形的性质以及两点间的距离等知识,正确把握相关性质是解题关键.
2.B
【分析】观察长方体,可知第一部分所对应的几何体在长方体中,上面有二个正方体,下面有二个正方体,再在BC选项中根据图形作出判断.
【详解】解:由长方体和第一部分所对应的几何体可知,
第一部分所对应的几何体上面有二个正方体,下面有二个正方体,并且与选项B相符.
故选:B.
【点睛】本题考查了认识立体图形,找到长方体中,第一部分所对应的几何体的形状是解题的关键.
3.B
【分析】根据长方体有六个面,展开后长方体相对的两个面不可能相邻进行判断.
【详解】A.中间两个细长方形相邻,错误;
B.各个相对的面没有相邻,正确;
C.中间两个大长方形相邻,错误;
D.图中有七个面,错误;
故选 B.
【点睛】本题考查几何体的展开,关键在于理解长方体有六个面,展开后长方体相对的两个面不可能相邻.
4.B
【分析】点动线,线动成面,将滚筒看做线,在运动过程中形成面.
【详解】解:滚筒看成是线,滚动的过程成形成面,
故选:B.
【点睛】本题考查点、线、面的关系;理解点动成线,线动成面的过程是解题的关键.
5.C
【分析】由AB=10cm,BC=4cm.于是得到AC=AB+BC=14cm,根据线段中点的定义由D是AC的中点,得到AD,根据线段的和差得到MD=AD﹣AM,于是得到结论.
【详解】解:∵AB=10cm,BC=4cm,
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
【点睛】此题主要考查了两点之间的距离,线段的和差、线段的中点的定义,利用线段差及中点性质是解题的关键.
6.B
【分析】先根据已知等式得出AB与AC的等量关系,再根据线段的中点定义可得出AC的长,从而可得出答案.
【详解】∵
∴,即
∵D为AC的中点,
∴
∴
故选:B.
【点睛】本题考查了线段的和差倍分、线段的中点定义,掌握线段的中点定义是解题关键.
7.C
【分析】根据补角的定义,即若两个角的和等于 ,就称这两个角互补,即可解答.
【详解】解:∵,
∴的补角等于 ,
故选:C
【点睛】本题主要考查了补角的定义,解题的关键是熟练掌握若两个角的和等于 ,就称这两个角互补.
8.B
【分析】观察所给几何体,可以直接得出答案.
【详解】解:A选项为圆柱,不合题意;
B选项为圆锥,符合题意;
C选项为三棱柱,不合题意;
D选项为球,不合题意;
故选B.
【点睛】本题考查常见几何体的识别,熟练掌握常见几何体的特征是解题的关键.圆锥面和一个截它的平面,组成的空间几何图形叫圆锥.
9.C
【分析】根据棱柱有两个底面求出侧面数,即可选择.
【详解】棱柱必有两个底面,则剩下7-2=5个面是侧面,所以为五棱柱.
故选C
【点睛】本题考查认识立体图形棱柱,解题的关键是知道棱柱必有两个底面.
10.B
【分析】根据几何体的形状是长方体,进行如图截面即可判断形状.
【详解】解:根据题意得:该几何体的截面形状是长方形.
故选:B
【点睛】本题考查了截一个几何体的应用,目的是培养学生的空间想象能力和动手操作能力.
11.
【分析】由∠AOB=∠COD=90°,∠AOC=∠BOD,进而∠AOC=∠BOD=108°-90°=18°,由此能求出∠BOC.
【详解】解: ∠AOB=∠COD=90°,
∠AOC=∠BOD, 又∠AOD=108°,
∠AOC=∠BOD=108°-90°=18°,
∠BOC=90°-18°=72°.
故答案为:.
【点睛】本题考查的是角的和差,两锐角的互余,掌握以上知识是解题的关键.
12. 143 45
【分析】根据补角定义直接解答.
【详解】的补角等于:180° =143°45′.
故答案为:143;45.
【点睛】此题属于基础题,较简单,本题考查补角的概念,解决本题的关键是熟记补角的概念.
13.125°##125度
【分析】若两个角的和为 则这两个角互余,若两个角的和为 则这两个角互补,根据定义直接可得答案.
【详解】解: 一个角的余角为35°,
这个角为:
则它的补角度数为:
故答案为:
【点睛】本题考查的是余角与补角的计算,掌握“余角与补角的含义”是解本题的关键.
14.14
【分析】如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,证明△A′MB′为等边三角形,即可解决问题.
【详解】解:如图,作点关于的对称点,点关于的对称点.
,
,
,
,
,
为等边三角形
,
的最大值为,
故答案为.
【点睛】本题考查等边三角形的判定和性质,两点之间线段最短,解题的关键是学会添加常用辅助线,学会利用两点之间线段最短解决最值问题
15.54°##54度
【分析】,通过,利用表示出,再根据角与角之间的关系,得到关于的方程,求解方程,即可得出答案.
【详解】解:设,
,
,
,
,解得:,
故答案为:.
【点睛】本题主要是考查了角的求解,熟练利用角与角之间的关系,求出未知角读书,这是解决本题的关键.
16.67
【分析】根据角平分线与角度的运算即可求解.
【详解】∵,
∴,
∵平分,
∴,
又∵,
∴,
∵,
∴
.
故答案为:67.
【点睛】此题主要考查角平分线的性质,解题的关键是熟知角度计算.
17.
【分析】根据为线段的中点,可得,即可求解.
【详解】D为AC的中点,
,
,
∵,
,
,
故答案为:.
【点睛】本题主要考查了与线段中点有关的计算,求比值,解题的关键在于能够根据题意求出.
18.a或a
【分析】分A、B在点D同侧,A、B在点D两侧,两种情况分别求解.
【详解】解:当A、B在点D同侧时,
∵AC=CB=a,BD=AD,
∴AD=3BD=3a,
∵M是BD中点,
∴BM=DM=a,
∴CM=BC+BM=a;
当A、B在点D两侧时,
∵AC=CB=a,BD=AD,
∴AB=2a,AD=a,BD=a,
∵M为BD中点,
∴DM=BM=BD=a,
∴CM=AB-AC-BM=a.
【点睛】本题考查了两点间的距离,中点的性质,解题的关键是灵活运用线段的和差,要分类讨论,以防遗漏.
19.(1)6;(2)5cm;(3)4cm或10cm.
【分析】(1)固定A为端点,数线段,依次类推,最后求和即可;
(2)根据AC=AD-CD=AC-2BC,计算即可;
(3)分点E在点A左边和右边两种情形求解.
【详解】(1)以A为端点的线段为:AC,AB,AD;以C为端点的线段为:CB,CD;
以B为端点的线段为:BD;
共有3+2+1=6(条);
故答案为:6.
(2)解:∵B为CD中点,cm
∴cm
∵cm
∴cm
(3)cm,cm
第一种情况:点E在线段AD上(点E在点A右侧).
cm
第二种情况:点E在线段DA延长线上(点E在点A左侧).
cm.
【点睛】本题考查了数线段,线段的中点,线段的和(差),熟练掌握线段的中点,灵活运用线段的和,差是解题的关键.
20.(1)DE=6cm,(2)DE=6cm,(3)见解析(4)见解析
【分析】(1)由AB=12cm,点D、E分别是AC和BC的中点,即可推出DE=(AC+BC)=AB=6cm,
(2)由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC=2cm,BE=EC=4cm,即可推出DE的长度,
(3)设AC=acm,然后通过点D、E分别是AC和BC的中点,即可推出DE=(AC+BC)=AB=cm,即可推出结论,
(4)由若OD、OE分别平分∠AOC和∠BOC,即可推出∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB=60°,即可推出∠DOE的度数与射线OC的位置无关.
【详解】(1)∵AB=12cm,点D、E分别是AC和BC的中点,C点为AB的中点,
∴AC=BC=6cm,
∴CD=CE=3cm,
∴DE=6cm,
(2)∵AB=12cm,
∴AC=4cm,
∴BC=8cm,
∵点D、E分别是AC和BC的中点,
∴CD=2cm,CE=4cm,
∴DE=6cm,
(3)设AC=acm,
∵点D、E分别是AC和BC的中点,
∴DE=CD+CE=(AC+BC)=AB=6cm,
∴不论AC取何值(不超过12cm),DE的长不变,
(4)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOE=∠DOC+∠COE=(∠AOC+∠COB)=∠AOB,
∵∠AOB=120°,
∴∠DOE=60°,
∴∠DOE的度数与射线OC的位置无关.
【点睛】本题主要考查角平分线和线段的中点的性质,关键在于认真的进行计算,熟练运用相关的性质定理.
21.(1)63;(2)∠DOE=82°;(3)∠DOE=n°
【分析】(1)根据角平分线的定义,和角的和差关系,可找到∠BOC和∠DOE的度数,代入数据即可;
(2)根据角平分线的定义,和角的和差关系,可找到∠BOC和∠DOE的度数,代入数据即可.
【详解】解:(1)∵OD、OE分别是∠AOB、∠AOC,
∴∠AOD=∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD+∠AOE=(∠AOB+∠AOC)=∠BOC,
∵∠BOC=126°
,∴∠DOE=63°,
故答案为:63.
(2)由①可知,∠DOE=∠BOC,
∵∠∠BOC=164°,
∴∠DOE=82°.
(3)∵OD、OE分别是∠AOB、∠AOC,
∴∠AOD=∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD﹣∠AOE=(∠AOB﹣∠AOC)=∠BOC,
∵∠BOC=n°,
∴∠DOE=n°.
【点睛】本题主要考查角平分线的定义,角的和差计算,根据图形,找到角之间的关系,是解题关键.
答案第1页,共2页
