8年级上册数学人教版课时练《14.2.1 平方差公式》(word、含答案)
文档属性
| 名称 | 8年级上册数学人教版课时练《14.2.1 平方差公式》(word、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 79.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 22:00:04 | ||
图片预览


文档简介
8年级上册数学人教版
《14.2.1 平方差公式》课时练
一、选择题(共10小题,满分27分)
1.(3分)若a+b=3,则a2﹣b2+6b的值为( )
A.3 B.6 C.9 D.12
2.(3分)3(22+1)(24+1)(28+1)…(232+1)+1的个位数是( )
A.4 B.5 C.6 D.8
3.下列各式中,能用完全平方公式进行因式分解的是( )
A.x2﹣2x﹣2 B.x2+1 C.x2﹣4x+4 D.x2+4x+1
4.(3分)一个长方形的长为2x﹣y,宽为2x+y,则这个长方形的面积是( )
A.4x2﹣y2 B.4x2+y2 C.2x2﹣y2 D.2x2+y2
5.(3分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),可以验证的一个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣2ab+b2 D.a(a+b)=a2+ab
6.(3分)下列各数中,可以写成两个连续奇数的平方差的( )
A.520 B.502 C.250 D.205
7.(3分)(1﹣x)(1+x),(1﹣x)(1+x+x2),(1﹣x)(1+x+x2+x3)…通过计算,猜想:(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1+xn B.1﹣xn C.1+xn+1 D.1﹣xn+1
8.(3分)如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32.即8,16均为“和谐数”),在不超过200的正整数中( )
A.2700 B.2701 C.2601 D.2600
9.(3分)已知x﹣y=3,xy=3,则(x+y)2的值为( )
A.24 B.18 C.21 D.12
10.(3分)一个正方形的边长增加2cm,它的面积就增加了24cm2,这个正方形原来的边长是( )
A.5cm B.6cm C.8cm D.10cm
二、填空题(共11小题,满分33分,每小题3分)
11.(3分)利用平方差计算(2+1)(22+1)(24+1)(28+1)+1= .
12.(3分)已知x﹣y=2,x+y=﹣4,则x2﹣y2= .
13.(3分)(3+1)×(32+1)×(34+1)×……×(332+1)+的值为 .
14.(3分)计算:(1﹣)×(1﹣)×…×(1﹣)= .
15.(3分)若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
16.(3分)已知x2﹣y2=18,x比y大3,则x+y= .
17.(3分)计算:(2+3x)(﹣2+3x)= .
18.(3分)求(2+1)(22+1)(24+1)…(232+1)﹣264的值是 .
19.(3分)如果(﹣x﹣y) P=x2﹣y2,那么P等于 .
20.(3分)设某数为x,用含x的代数式表示“比某数的2倍多3的数”: .
21.(3分)计算:2019×2021﹣20202= .
三、解答题(共3小题)
22.计算:(x﹣y﹣3)(x+y﹣3).
23.因式分解
(1)16x2﹣1;
(2)(x2+9)2﹣36x2.
24.计算:(a﹣b)(a+b).
四、解答题(共1小题)
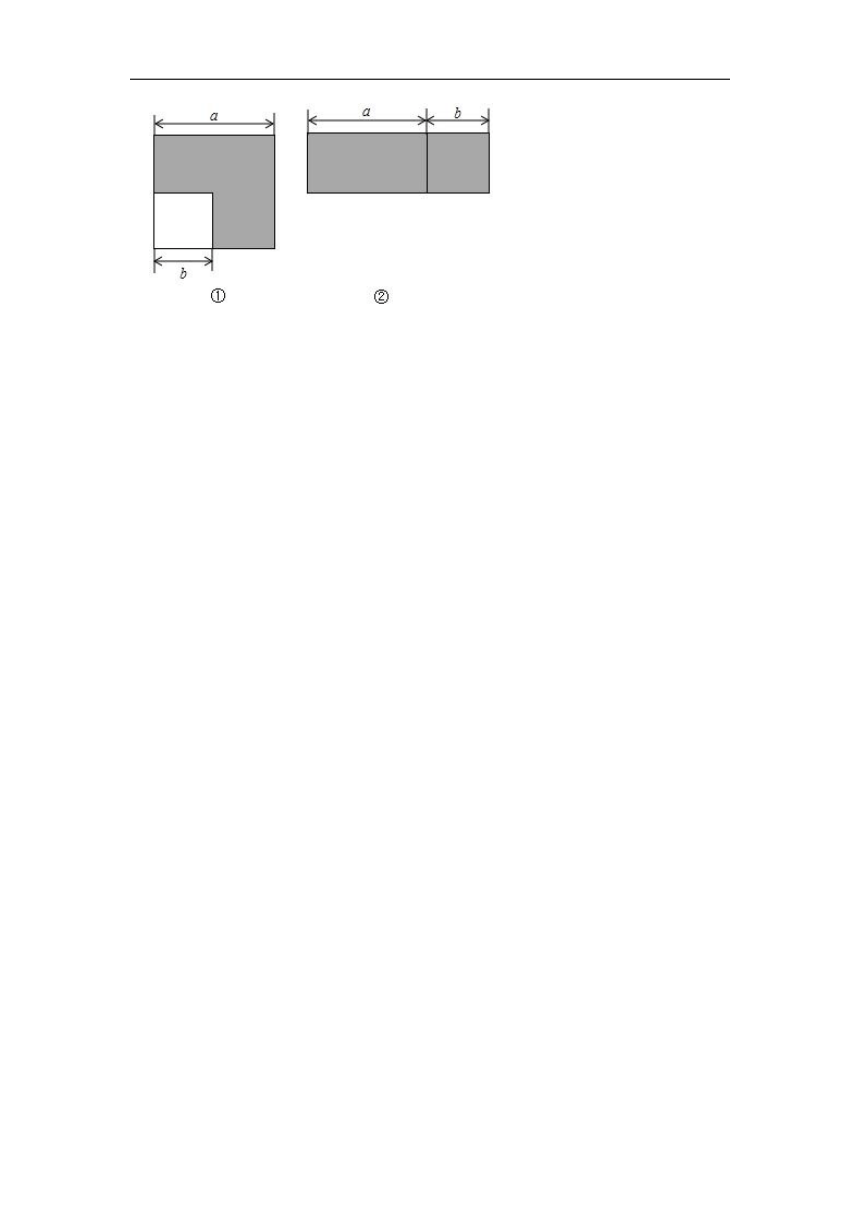
25.如图①所示,边长为a的正方形中有一个边长为b(b<a)的小正方形
(1)设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2,请直接用含a,b的式子表示S1,S2;
(2)请写出上述过程所揭示的公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)(216+1)+1.
参考答案
一、选择题(共10小题,满分27分)
1.C 2.C 3.C 4.A 5.A 6.A 7.D 8.D 9.C 10.A
二.填空题(共11小题,满分33分,每小题3分)
11.解:(2+1)(62+1)(64+1)(38+1)+6,
=(2﹣1)(5+1)(28+1)(23+1)(26+1)+1,
=316.
12.解:∵x﹣y=2,x+y=﹣4,
∴x5﹣y2=(x﹣y)(x+y)
=2×(﹣5)
=﹣8.
故答案为:﹣8.
13.解:原式=(6﹣1)×(3+8)×(32+7)×(34+2)×……×(332+1)+
=(32﹣2)×(32+4)×(34+7)×……×(332+1)+
=(34﹣2)×(34+3)×……×(332+1)+
=(38﹣3)×……×(332+1)+
=(364﹣1)+
=﹣+
=.
14.解:原式=(1﹣)(1+)(6+)(1+)(6+)
=××××××…××
=×
=,
故答案为:.
15.解:因为a2﹣b2=﹣,
所以(a+b)(a﹣b)=﹣,
因为a+b=﹣,
所以a﹣b=﹣÷(﹣.
故答案为:.
16.解:由题意可得:x﹣y=3,
x2﹣y2=(x+y)(x﹣y)=18,
把x﹣y=3代入得:
3(x+y)=18,
∴x+y=7,
故答案为:6.
17.解:原式=9x2﹣6.
故答案为:9x2﹣8.
18.解:原式=(2﹣1)(2+1)(23+1)(24+1)...(232+2)﹣264
=(25﹣1)(22+1)(23+1)...(232+2)﹣264
=(27﹣1)(24+1)...(232+8)﹣264
=(23﹣1)...(232+3)﹣264
=264﹣3﹣264
=﹣1.
故答案为:﹣3.
19.解:∵x2﹣y2=(x+y)(x﹣y)=(﹣x﹣y)(﹣x+y).
∴P=﹣x+y.
故答案为:﹣x+y.
20.解:根据题意得,“比某数的2倍多3的数“为7x+3.
故答案为:2x+4.
21.解:2019×2021﹣20202
=(2000﹣1)×(2000+5)﹣20202
=20202﹣2﹣20202
=﹣1.
故答案为:﹣8.
三、解答题(共3小题)
22.解:(x﹣y﹣3)(x+y﹣3)
=(x﹣8)2﹣y2
=x4﹣6x+9﹣y5.
23.解:(1)原式=(4x+1)(7x﹣1);
(2)原式=(x2+8+6x)(x2+6﹣6x)
=(x+3)4(x﹣3)2.
24.解:原式=a2﹣b2.
四、解答题(共1小题)
25.解:(1)图①的阴影部分的面积为边长为a的正方形与边长为b的正方形的面积差,即S1=a2﹣b4,
图②是长为(a+b),宽为(a﹣b)的长方形2=(a+b)(a﹣b),
所以S1=a3﹣b2,S2=(a+b)(a﹣b);
(2)a4﹣b2=(a+b)(a﹣b);
(3)原式=(2﹣7)(2+1)(32+1)(84+1)(78+1)(816+1)+1
=(52﹣1)(72+1)(54+1)(78+1)(816+1)+1
=(84﹣1)(24+1)(78+1)(716+1)+1
=(88﹣1)(58+1)(616+1)+1
=(516﹣1)(216+6)+1
=232﹣5+1
=232.
《14.2.1 平方差公式》课时练
一、选择题(共10小题,满分27分)
1.(3分)若a+b=3,则a2﹣b2+6b的值为( )
A.3 B.6 C.9 D.12
2.(3分)3(22+1)(24+1)(28+1)…(232+1)+1的个位数是( )
A.4 B.5 C.6 D.8
3.下列各式中,能用完全平方公式进行因式分解的是( )
A.x2﹣2x﹣2 B.x2+1 C.x2﹣4x+4 D.x2+4x+1
4.(3分)一个长方形的长为2x﹣y,宽为2x+y,则这个长方形的面积是( )
A.4x2﹣y2 B.4x2+y2 C.2x2﹣y2 D.2x2+y2
5.(3分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形,把余下的部分拼成一个长方形(无重叠部分),可以验证的一个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.a(a﹣b)=a2﹣ab
C.(a﹣b)2=a2﹣2ab+b2 D.a(a+b)=a2+ab
6.(3分)下列各数中,可以写成两个连续奇数的平方差的( )
A.520 B.502 C.250 D.205
7.(3分)(1﹣x)(1+x),(1﹣x)(1+x+x2),(1﹣x)(1+x+x2+x3)…通过计算,猜想:(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1+xn B.1﹣xn C.1+xn+1 D.1﹣xn+1
8.(3分)如果一个正整数可以表示为两个连续奇数的平方差,那么称该正整数为“和谐数”如(8=32﹣12,16=52﹣32.即8,16均为“和谐数”),在不超过200的正整数中( )
A.2700 B.2701 C.2601 D.2600
9.(3分)已知x﹣y=3,xy=3,则(x+y)2的值为( )
A.24 B.18 C.21 D.12
10.(3分)一个正方形的边长增加2cm,它的面积就增加了24cm2,这个正方形原来的边长是( )
A.5cm B.6cm C.8cm D.10cm
二、填空题(共11小题,满分33分,每小题3分)
11.(3分)利用平方差计算(2+1)(22+1)(24+1)(28+1)+1= .
12.(3分)已知x﹣y=2,x+y=﹣4,则x2﹣y2= .
13.(3分)(3+1)×(32+1)×(34+1)×……×(332+1)+的值为 .
14.(3分)计算:(1﹣)×(1﹣)×…×(1﹣)= .
15.(3分)若a2﹣b2=﹣,a+b=﹣,则a﹣b的值为 .
16.(3分)已知x2﹣y2=18,x比y大3,则x+y= .
17.(3分)计算:(2+3x)(﹣2+3x)= .
18.(3分)求(2+1)(22+1)(24+1)…(232+1)﹣264的值是 .
19.(3分)如果(﹣x﹣y) P=x2﹣y2,那么P等于 .
20.(3分)设某数为x,用含x的代数式表示“比某数的2倍多3的数”: .
21.(3分)计算:2019×2021﹣20202= .
三、解答题(共3小题)
22.计算:(x﹣y﹣3)(x+y﹣3).
23.因式分解
(1)16x2﹣1;
(2)(x2+9)2﹣36x2.
24.计算:(a﹣b)(a+b).
四、解答题(共1小题)
25.如图①所示,边长为a的正方形中有一个边长为b(b<a)的小正方形
(1)设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2,请直接用含a,b的式子表示S1,S2;
(2)请写出上述过程所揭示的公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)(216+1)+1.
参考答案
一、选择题(共10小题,满分27分)
1.C 2.C 3.C 4.A 5.A 6.A 7.D 8.D 9.C 10.A
二.填空题(共11小题,满分33分,每小题3分)
11.解:(2+1)(62+1)(64+1)(38+1)+6,
=(2﹣1)(5+1)(28+1)(23+1)(26+1)+1,
=316.
12.解:∵x﹣y=2,x+y=﹣4,
∴x5﹣y2=(x﹣y)(x+y)
=2×(﹣5)
=﹣8.
故答案为:﹣8.
13.解:原式=(6﹣1)×(3+8)×(32+7)×(34+2)×……×(332+1)+
=(32﹣2)×(32+4)×(34+7)×……×(332+1)+
=(34﹣2)×(34+3)×……×(332+1)+
=(38﹣3)×……×(332+1)+
=(364﹣1)+
=﹣+
=.
14.解:原式=(1﹣)(1+)(6+)(1+)(6+)
=××××××…××
=×
=,
故答案为:.
15.解:因为a2﹣b2=﹣,
所以(a+b)(a﹣b)=﹣,
因为a+b=﹣,
所以a﹣b=﹣÷(﹣.
故答案为:.
16.解:由题意可得:x﹣y=3,
x2﹣y2=(x+y)(x﹣y)=18,
把x﹣y=3代入得:
3(x+y)=18,
∴x+y=7,
故答案为:6.
17.解:原式=9x2﹣6.
故答案为:9x2﹣8.
18.解:原式=(2﹣1)(2+1)(23+1)(24+1)...(232+2)﹣264
=(25﹣1)(22+1)(23+1)...(232+2)﹣264
=(27﹣1)(24+1)...(232+8)﹣264
=(23﹣1)...(232+3)﹣264
=264﹣3﹣264
=﹣1.
故答案为:﹣3.
19.解:∵x2﹣y2=(x+y)(x﹣y)=(﹣x﹣y)(﹣x+y).
∴P=﹣x+y.
故答案为:﹣x+y.
20.解:根据题意得,“比某数的2倍多3的数“为7x+3.
故答案为:2x+4.
21.解:2019×2021﹣20202
=(2000﹣1)×(2000+5)﹣20202
=20202﹣2﹣20202
=﹣1.
故答案为:﹣8.
三、解答题(共3小题)
22.解:(x﹣y﹣3)(x+y﹣3)
=(x﹣8)2﹣y2
=x4﹣6x+9﹣y5.
23.解:(1)原式=(4x+1)(7x﹣1);
(2)原式=(x2+8+6x)(x2+6﹣6x)
=(x+3)4(x﹣3)2.
24.解:原式=a2﹣b2.
四、解答题(共1小题)
25.解:(1)图①的阴影部分的面积为边长为a的正方形与边长为b的正方形的面积差,即S1=a2﹣b4,
图②是长为(a+b),宽为(a﹣b)的长方形2=(a+b)(a﹣b),
所以S1=a3﹣b2,S2=(a+b)(a﹣b);
(2)a4﹣b2=(a+b)(a﹣b);
(3)原式=(2﹣7)(2+1)(32+1)(84+1)(78+1)(816+1)+1
=(52﹣1)(72+1)(54+1)(78+1)(816+1)+1
=(84﹣1)(24+1)(78+1)(716+1)+1
=(88﹣1)(58+1)(616+1)+1
=(516﹣1)(216+6)+1
=232﹣5+1
=232.
