第二十四章 圆(原卷版+解析版)【满分计划】2022-2023学年九年级数学上册阶段性测试卷(人教版)
文档属性
| 名称 | 第二十四章 圆(原卷版+解析版)【满分计划】2022-2023学年九年级数学上册阶段性测试卷(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 775.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览




文档简介
第二十四章 圆
一、单选题
1.如图,内接于,AD是的直径,若,则的度数是( )
A.60° B.65° C.70° D.75°
2.如图,四边形为矩形,,.点P是线段上一动点,点M为线段上一点.,则的最小值为( )
A. B. C. D.
3.如图,AB 为⊙O 的直径,点 D 是弧 AC 的中点,过点 D 作 DE⊥AB 于点 E,延长 DE 交⊙O 于点 F,若 AC=12,AE=3,则⊙O 的直径长为( )
A.7.5 B.15
C.16 D.18
4.如图,在中,,,,以点为圆心,为半径的圆与所在直线的位置关系是( )
A.相交 B.相离 C.相切 D.无法判断
5.以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=25°,则∠OCD=( ).
A.50° B.40° C.70° D.30°
6.如图,在以AB为直径的⊙O中,点C为圆上的一点,,弦于点E,弦AF交CE于点H,交BC于点G,若点H是AG的中点,则的度数为( )
A.18° B.21° C.22.5° D.30°
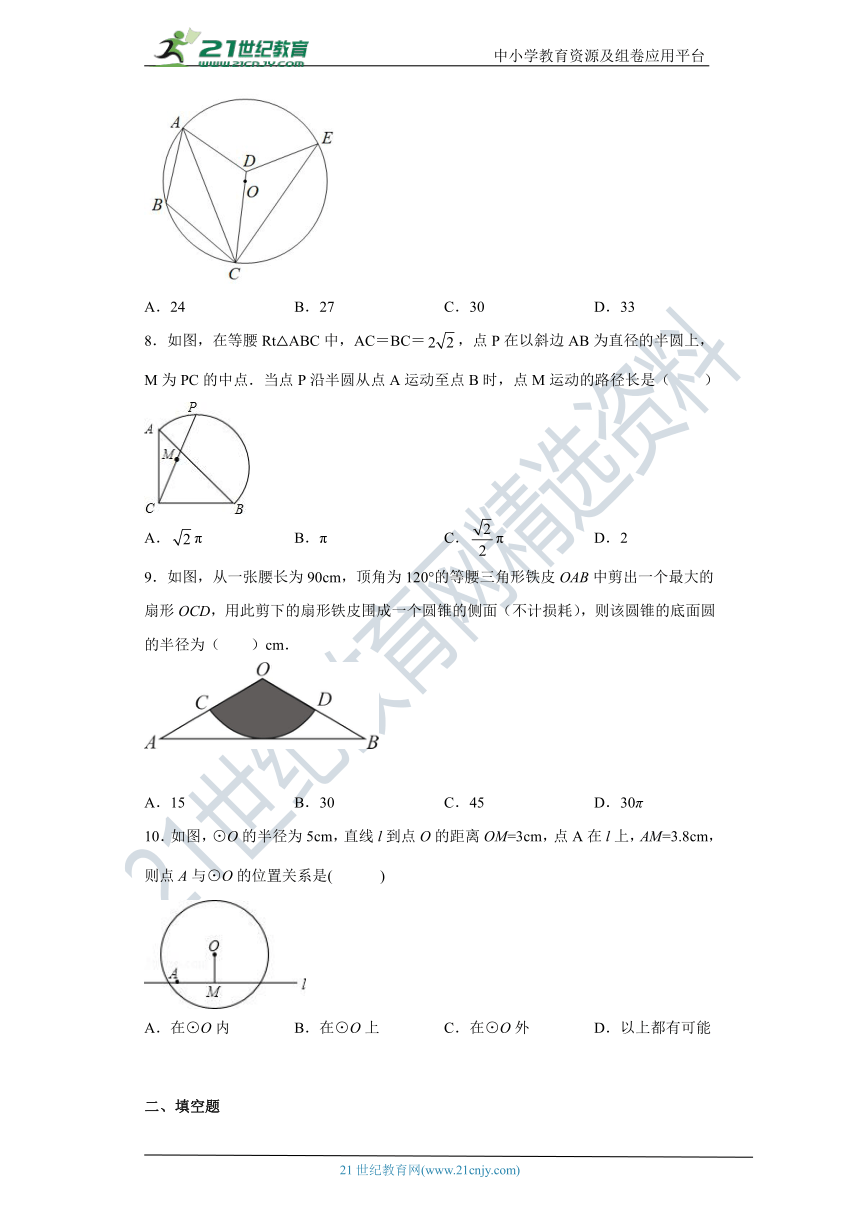
7.如图,⊙O是△ABC的外接圆,将△ABC绕点C顺时针旋转至△EDC,使点E在⊙O上,再将△EDC沿CD翻折,点E恰好与点A重合,已知∠BAC=36°,则∠DCE的度数是( )
A.24 B.27 C.30 D.33
8.如图,在等腰Rt△ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A.π B.π C.π D.2
9.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面圆的半径为( )cm.
A.15 B.30 C.45 D.30π
10.如图,⊙O的半径为5cm,直线l到点O的距离OM=3cm,点A在l上,AM=3.8cm,则点A与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.以上都有可能
二、填空题
11.如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB=_______.
12.如图,四边形ABCD内接于⊙O,∠A=125°,则∠C的度数为______.
13.已知圆锥的侧面积是8π,底面半径是2,则圆锥的母线长是_________.
14.如图,,,以为直径作半圆,圆心为点;以点为圆心,为半径作,过点作的平行线交两弧于点、,则阴影部分的面积是________.
15.如图,将三角形AOC绕点O顺时针旋转120°得三角形BOD,已知OA=4,OC=1,那么图中阴影部分的面积为_____.(结果保留π)
16.从一块直径是的圆中剪出一个圆心角为90°的扇形,将减下来的扇形围成一个圆锥,圆锥底面圆的半径是___________.
17.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是 _____.
三、解答题
18.如图,已知抛物线的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:(),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
19.如图,在菱形ABCD中,,P为AC,BD的交点,经过A,B,P三点.
(1)求证:AB为的直径.
(2)请用无刻度的直尺在圆上找一点Q,使得BP=PQ(不写作法,保留作图痕迹).
20.如图,CD与EF是⊙O的直径,连接CE、CF,延长CE到A,连接AD并延长,交CF的延长线于点B,过点F作⊙O的切线交AB于点G,点D是AB的中点.
(1)求证:;
(2)若,,求FG的长.
21.在《折叠圆形纸片》综合实践课上,小东同学展示了如下的操作及问题:
(1)如图1,的半径为4cm,通过折叠圆形纸片,使得劣弧AB沿弦AB折叠后恰好过圆心,求AB长;
(2)如图2,弦AB,垂足为点C,劣弧AB沿弦AB折叠后经过的中点D,,求的半径.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】首先连接CD,由AD是的直径,根据直径所对的圆周角是直角,可求得,又由圆周角定理,可得,再用三角形内角和定理求得答案.
【详解】解:连接CD,
∵AD是的直径,
∴.
∵,
∴.
故选:C.
【点睛】本题考查了圆周角定理、三角形的内角和定理.熟练掌握圆周角定理是解此题的关键.
2.D
【分析】证明,得出点M在O点为圆心,以AO为半径的圆上,从而计算出答案.
【详解】设AD的中点为O,以O点为圆心,AO为半径画圆
∵四边形为矩形
∴
∵
∴
∴
∴点M在O点为圆心,以AO为半径的圆上
连接OB交圆O与点N
∵点B为圆O外一点
∴当直线BM过圆心O时,BM最短
∵,
∴
∴
∵
故选:D.
【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.
3.B
【分析】连接OF,首先证明AC=DF=12,设OA=OF=x,在Rt△OEF中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,,
∵点D是弧AC的中点,
∴,
∴,
∴AC=DF=12,
∴EF=DF=6,
设OA=OF=x,
在Rt△OEF中,则有x2=62+(x-3)2,
解得x=,
∴AB=2x=15,
故选:B.
【点睛】本题考查了勾股定理,垂径定理,圆心角,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题.
4.A
【分析】过点C作CD⊥AB于点D,由题意易得AB=5,然后可得,进而根据直线与圆的位置关系可求解.
【详解】解:过点C作CD⊥AB于点D,如图所示:
∵,,,
∴,
根据等积法可得,
∴,
∵以点为圆心,为半径的圆,
∴该圆的半径为,
∵,
∴圆与AB所在的直线的位置关系为相交,
故选A.
【点睛】本题主要考查直线与圆的位置关系,熟练掌握直线与圆的位置关系是解题的关键.
5.C
【分析】根据圆周角定理求出∠DOB,根据等腰三角形性质求出∠OCD=∠ODC,根据三角形内角和定理求出即可.
【详解】解:连接OD,
∵∠DAB=25°,
∴∠BOD=2∠DAB=50°,
∴∠COD=90°-50°=40°,
∵OC=OD,
∴∠OCD=∠ODC=(180°-∠COD)=70°,
故选:C.
【点睛】本题考查了圆周角定理,等腰三角形性质,三角形内角和定理的应用,主要考查学生的推理能力,题目比较典型,难度适中.
6.D
【分析】由圆周角定理可求∠ACB=90°,由弧的关系得出角的关系,进而可求∠ABC=30°,∠CAB=60°,由直角三角形的性质可求∠CAH=∠ACE=30°,即可求解.
【详解】解:∵AB是直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵,
∴∠CAB=2∠ABC,
∴∠ABC=30°,∠CAB=60°,
∵CD⊥AB,
∴∠AEC=90°,
∴∠ACE=30°,
∵点H是AG的中点,∠ACB=90°,
∴AH=CH=HG,
∴∠CAH=∠ACE=30°,
∵∠CAF=∠CBF,
∴∠CBF=30°,
故选:D.
【点睛】本题考查了圆周角定理,圆心角、弧、弦的关系,直角三角形的性质,求出∠CAB的度数是本题的关键.
7.B
【分析】延长CD交⊙O于点F,连接AF,则由CD经过圆心O可得∠CAF=90°,先由翻折得到∠BCA=∠DCA,AB=AD,∠CAD=∠CAB=36°,然后得到∠FAO=54°,再由圆周角定理得到AB=AF,进而得到AF=AD,也就有∠ADF=∠AFD=63°,再由三角形的外角性质得到∠ACD的大小,最后由旋转的性质得到∠DCE的大小.
【详解】解:如图,延长CD交⊙O于点F,连接AF,
由题可知,,
垂直平分,
CD经过圆心O,
∴∠CAF=90°,
由翻折得,∠DCA=∠BCA,AB=AD,∠CAD=∠CAB=36°,
∴∠FAO=∠CAF﹣∠CAD=90°﹣36°=54°,AB=AF,
∴AF=AD,
∴∠ADF=∠AFD=(180°﹣∠DAF)=(180°﹣54°)=63°,
∵∠ADF是△ACD的外角,
∴∠ACD=∠ADF﹣∠CAD=63°﹣36°=27°,
∴∠BCA=27°,
由旋转的性质得,∠DCE=∠BCA=27°,
故选:B.
【点睛】本题考查了圆周角定理、等腰三角形的判定与性质、旋转的性质、翻折的性质、三角形的外角性质,解题的关键是熟知“直径所对的圆周角为直角”求得∠DAF的大小.
8.B
【分析】取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,利用勾股定理得到AB的长,进而可求出OC,OP的长,求得∠CMO=90°,于是得到点M在以OC为直径的圆上,然后根据圆的周长公式计算点M运动的路径长.
【详解】解:取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,
∵在等腰Rt△ABC中,AC=BC=2,
∴AB=BC=4,
∴OC=OP=AB=2,
∵∠ACB=90°,
∴C在⊙O上,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
P点在A点时,M点在E点;P点在B点时,M点在F点.
∵O是AB中点,E是AC中点,
∴OE是△ABC的中位线,
∴OE//BC,OE=BC=,
∴OE⊥AC,
同理OF⊥BC,OF=,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长=×π×2=π.
故选:B.
【点睛】本题考查了等腰三角形的性质,勾股定理,正方形的判定与性质,圆周角定理,以及动点的轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用圆周角定理确定M点的轨迹为以EF为直径的半圆.
9.A
【分析】作出等腰三角形底边上的高线OE,首先根据直角三角形30°所对的直角边等于斜边的一半求出等腰三角形底边上的高线OE的长度,即得到扇形OCD所在的圆的半径R,然后根据弧长公式求出的长度,的长度即为圆锥底面圆的周长,最后根据周长求出半径即可.
【详解】如图,过点O作OE⊥AB,垂足为E,
∵△OAB为顶角为120°的等腰三角形,
∴=30°,cm,
∴cm,
设圆锥的底面圆半径为rcm,根据题意得,
,
解得,
所以该圆锥的底面圆的半径为15cm,
故选A.
【点睛】本题考查了直角三角形30°所对的直角边等于斜边的一半、扇形的弧长公式、圆的周长公式,准确将扇形的弧长转化为底面圆的周长是解决本题的关键.
10.A
【详解】如图,连接OA,则在直角△OMA中,根据勾股定理得到OA=.
∴点A与⊙O的位置关系是:点A在⊙O内.
故选A.
11.16
【分析】连接,由垂径定理可得,在中利用勾股定理即可求得的长,进而求得.
【详解】解:连接,
∵OE⊥AB于E,
∴,
在中,,OE=6,
∴,
∴,
故答案为:
【点睛】本题考查了垂径定理和勾股定理,构造直角三角形是解题的关键.
12.55°##55度
【分析】根据圆内接四边形的性质得出∠A+∠C=180°,再求出答案即可.
【详解】解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠A=125°,
∴∠C=180°-125°=55°,
故答案为:55°.
【点睛】本题考查了圆内接四边形的性质和圆周角定理,能熟记圆内接四边形的对角互补是解此题的关键.
13.4
【分析】设母线长为R,可得底面周长为4π,再由圆锥的侧面积是8π,可得,即可求解.
【详解】解:设母线长为R,
∵底面半径是2,
∴底面周长=2×2π=4π,
∵圆锥的侧面积是8π,
∴,解得:R=4.
故答案为:4
【点睛】本题主要考查了求圆锥的母线长,熟记圆锥的侧面积公式是解答本题的关键,难度不大.
14.
【分析】连接CE,如图,利用平行线的性质得∠COE=∠EOB=90°,再利用勾股定理计算出OE=,利用余弦的定义得到∠OCE=60°,然后根据扇形面积公式,利用
S阴影部分=S扇形BCE S△OCE S扇形BOD进行计算即可.
【详解】解:连接CE,如图,
∵AC⊥BC,
∴∠ACB=90°,
∵AC∥OE,
∴∠COE=∠EOB=90°,
∵OC=1,CE=2,
∴OE=,cos∠OCE=,
∴∠OCE=60°,
∴S阴影部分=S扇形BCE S△OCE S扇形BOD=,
故答案为.
【点睛】本题考查了扇形面积的计算:求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
15.5π
【分析】根据旋转的性质可以得到阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积,利用扇形的面积公式计算即可求解.
【详解】∵△AOC≌△BOD,∴阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积5π.
故答案为5π.
【点睛】本题考查了旋转的性质以及扇形的面积公式,正确理解:阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积是解题的关键.
16.0.5##
【分析】先利用等腰直角三角形的性质得到,设圆锥的底面圆的半径为r,利用弧长公式得到,然后解方程即可.
【详解】解:如图:
∵,
∴,
∵,,
∴,
设圆锥的底面圆的半径为r,
根据题意得,
解得,
即圆锥的底面圆的半径为.
故答案为:0.5
【点睛】此题考查了弧长公式,90度的圆周角所对的弦是直径,勾股定理,由90度的圆周角所对的弦是直径及勾股定理求出AB的长是解题的关键.
17.36
【分析】根据正五边形的性质可求出每个内角的度数为108°,根据等腰三角形的性质可求出∠EAC=∠DCA=72°,进而可得四边形AEDF是平行四边形,求出∠DFC的度数,再根据三角形的内角和定理求出答案即可.
【详解】解:∵正五边形ABCDE,
∴∠ABC=∠EAB==108°,AB=BC=CD=DE=AE,
∴∠ACB=∠BAC==36°,
∴∠EAC=∠DCA=108°﹣36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴DE∥AC,
又∵DE=AE=AF,
∴四边形AEDF是平行四边形,
∴AE∥DF,
∴∠DFC=∠EAC=72°=∠DCA,
∴∠FDC=180°﹣72°﹣72°=36°,
故答案为:36°.
【点睛】本题考查正多边形与圆,掌握正五边形的性质以及三角形的内角和定理是正确解答的前提.
18.(1),M(,);(2),(,);(3)证明见试题解析.
【详解】试题分析:(1)利用配方法把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;
(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;
(3)设点P坐标为(x,).根据NPAB=,列出方程,解方程得到点P坐标,再计算得出,由勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
试题解析:(1)∵=,∴抛物线的解析式化为顶点式为:,顶点M的坐标是(,);
(2)∵,∴当y=0时,,解得x=1或6,∴A(1,0),B(6,0),∵x=0时,y=﹣3,∴C(0,﹣3).连接BC,则BC与对称轴x=的交点为R,连接AR,则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,最小值为BC==.设直线BC的解析式为,∵B(6,0),C(0,﹣3),∴,解得:,∴直线BC的解析式为:,令x=,得y==,∴R点坐标为(,);
(3)设点P坐标为(x,).∵A(1,0),B(6,0),∴N(,0),∴以AB为直径的⊙N的半径为AB=,∴NP=,即,移项得,,得:,整理得:,解得(与A重合,舍去),,(在对称轴的右侧,舍去),(与B重合,舍去),∴点P坐标为(2,2).∵M(,),N(,0),∴==,==, ==,∴,∴∠MPN=90°,∵点P在⊙N上,∴直线MP是⊙N的切线.
考点:1.二次函数综合题;2.最值问题;3.切线的判定;4.压轴题.
19.(1)见解析
(2)见解析
【分析】(1)根据菱形的性质可得∠APB=90°,再由90°角所对的弦为圆的直径,即可求证;
(2)延长DA交于点Q,连接PQ,则PQ即为所求,理由:连接BQ,根据AB为的直径,可得∠AQB=90°,从而得到∠BDQ+∠PBQ=90°,再由菱形的性质可得∠ABP+∠PBQ=90°,再由圆周角定理,即可求解.
(1)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,即∠APB=90°,
∵经过A,B,P三点.
∴AB为的直径;
(2)
解:如图,延长DA交于点Q,即为所求,
理由:连接BQ,
∵AB为的直径,
∴∠AQB=90°,
∴∠BDQ+∠PBQ=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD,
∴∠APB=90°,∠BDQ=∠ABP,
∴∠ABP+∠PBQ=90°,
∵∠ABP+∠BAP=90°,
∴∠BAP=∠PBQ,
∵∠BAP=∠BQP,
∴∠PBQ =∠BQP,
∴BP=PQ.
【点睛】本题主要考查了圆周角定理,菱形的性质,熟练掌握圆周角定理,菱形的性质是解题的关键.
20.(1)见解析;
(2)
【分析】(1)连接DE,根据CD和EF都是⊙O的直径得到∠DEA=∠ECF=90°,根据直角三角形的性质得到CD=AD=BD,利用等腰三角形三线合一的性质推出∠ADE=∠CDE,进而得到∠ADE=∠OED,即可得到;
(2)根据直角三角形斜边上的中线求得,勾股定理求得,由(1)可得,根据切线的性质可得,根据,代入数值,即可得到FC.
(1)
证明:连接DE,
∵CD和EF都是⊙O的直径,
∴∠DEA=∠ECF=90°,
∵D是AB的中点,
∴CD=AD=BD,
∴∠ADE=∠CDE,
∵OD=OE,
∴∠OED=∠CDE,
∴∠ADE=∠OED,
∴;
(2)
连接DF,
∵CD是⊙O的直径,
∴∠DFC=90°,
∴∠DFC=∠FCE=∠CED=90°,
∴四边形CEDF是矩形,
∴FC=DE,DE∥BC,
∴,
∴AE=CE,
∴DE是△ABC的中位线,
∴,
∵AB=2CD=5,AC=3,
∴,
∴FC=2.
是的切线,
【点睛】此题考查了圆周角定理,矩形的判定定理及性质定理,勾股定理,三角形中位线的性质,熟记圆周角定理是解题的关键.
21.(1)cm
(2)cm
【分析】(1)如图1,作交于,交于,连接,由题意知,,,在中,由勾股定理得求出的值,进而可求的值;
(2)如图2,延长交于,连接,设半径为,由题意知,由折叠和中点的性质可知,在中,由勾股定理得,即,求出满足要求的解即可.
(1)
解:如图1,作交于,交于,连接
由题意知,,
在中,由勾股定理得
∴
∴的长为.
(2)
解:如图2,延长交于,连接,设半径为
由题意知,由折叠和中点的性质可知,
在中,由勾股定理得,即
解得:,(不合题意,舍去)
∴半径的长为.
【点睛】本题考查了垂径定理,折叠的性质,勾股定理等知识.解题的关键在于对知识的熟练掌握与灵活运用.
答案第1页,共2页
一、单选题
1.如图,内接于,AD是的直径,若,则的度数是( )
A.60° B.65° C.70° D.75°
2.如图,四边形为矩形,,.点P是线段上一动点,点M为线段上一点.,则的最小值为( )
A. B. C. D.
3.如图,AB 为⊙O 的直径,点 D 是弧 AC 的中点,过点 D 作 DE⊥AB 于点 E,延长 DE 交⊙O 于点 F,若 AC=12,AE=3,则⊙O 的直径长为( )
A.7.5 B.15
C.16 D.18
4.如图,在中,,,,以点为圆心,为半径的圆与所在直线的位置关系是( )
A.相交 B.相离 C.相切 D.无法判断
5.以原点O为圆心的圆交x轴于A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=25°,则∠OCD=( ).
A.50° B.40° C.70° D.30°
6.如图,在以AB为直径的⊙O中,点C为圆上的一点,,弦于点E,弦AF交CE于点H,交BC于点G,若点H是AG的中点,则的度数为( )
A.18° B.21° C.22.5° D.30°
7.如图,⊙O是△ABC的外接圆,将△ABC绕点C顺时针旋转至△EDC,使点E在⊙O上,再将△EDC沿CD翻折,点E恰好与点A重合,已知∠BAC=36°,则∠DCE的度数是( )
A.24 B.27 C.30 D.33
8.如图,在等腰Rt△ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A.π B.π C.π D.2
9.如图,从一张腰长为90cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面圆的半径为( )cm.
A.15 B.30 C.45 D.30π
10.如图,⊙O的半径为5cm,直线l到点O的距离OM=3cm,点A在l上,AM=3.8cm,则点A与⊙O的位置关系是( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.以上都有可能
二、填空题
11.如图,OE⊥AB于E,若⊙O的半径为10,OE=6,则AB=_______.
12.如图,四边形ABCD内接于⊙O,∠A=125°,则∠C的度数为______.
13.已知圆锥的侧面积是8π,底面半径是2,则圆锥的母线长是_________.
14.如图,,,以为直径作半圆,圆心为点;以点为圆心,为半径作,过点作的平行线交两弧于点、,则阴影部分的面积是________.
15.如图,将三角形AOC绕点O顺时针旋转120°得三角形BOD,已知OA=4,OC=1,那么图中阴影部分的面积为_____.(结果保留π)
16.从一块直径是的圆中剪出一个圆心角为90°的扇形,将减下来的扇形围成一个圆锥,圆锥底面圆的半径是___________.
17.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是 _____.
三、解答题
18.如图,已知抛物线的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:(),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
19.如图,在菱形ABCD中,,P为AC,BD的交点,经过A,B,P三点.
(1)求证:AB为的直径.
(2)请用无刻度的直尺在圆上找一点Q,使得BP=PQ(不写作法,保留作图痕迹).
20.如图,CD与EF是⊙O的直径,连接CE、CF,延长CE到A,连接AD并延长,交CF的延长线于点B,过点F作⊙O的切线交AB于点G,点D是AB的中点.
(1)求证:;
(2)若,,求FG的长.
21.在《折叠圆形纸片》综合实践课上,小东同学展示了如下的操作及问题:
(1)如图1,的半径为4cm,通过折叠圆形纸片,使得劣弧AB沿弦AB折叠后恰好过圆心,求AB长;
(2)如图2,弦AB,垂足为点C,劣弧AB沿弦AB折叠后经过的中点D,,求的半径.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】首先连接CD,由AD是的直径,根据直径所对的圆周角是直角,可求得,又由圆周角定理,可得,再用三角形内角和定理求得答案.
【详解】解:连接CD,
∵AD是的直径,
∴.
∵,
∴.
故选:C.
【点睛】本题考查了圆周角定理、三角形的内角和定理.熟练掌握圆周角定理是解此题的关键.
2.D
【分析】证明,得出点M在O点为圆心,以AO为半径的圆上,从而计算出答案.
【详解】设AD的中点为O,以O点为圆心,AO为半径画圆
∵四边形为矩形
∴
∵
∴
∴
∴点M在O点为圆心,以AO为半径的圆上
连接OB交圆O与点N
∵点B为圆O外一点
∴当直线BM过圆心O时,BM最短
∵,
∴
∴
∵
故选:D.
【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.
3.B
【分析】连接OF,首先证明AC=DF=12,设OA=OF=x,在Rt△OEF中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,,
∵点D是弧AC的中点,
∴,
∴,
∴AC=DF=12,
∴EF=DF=6,
设OA=OF=x,
在Rt△OEF中,则有x2=62+(x-3)2,
解得x=,
∴AB=2x=15,
故选:B.
【点睛】本题考查了勾股定理,垂径定理,圆心角,弧,弦之间的关系等知识,解题的关键是学会利用参数构建方程解决问题.
4.A
【分析】过点C作CD⊥AB于点D,由题意易得AB=5,然后可得,进而根据直线与圆的位置关系可求解.
【详解】解:过点C作CD⊥AB于点D,如图所示:
∵,,,
∴,
根据等积法可得,
∴,
∵以点为圆心,为半径的圆,
∴该圆的半径为,
∵,
∴圆与AB所在的直线的位置关系为相交,
故选A.
【点睛】本题主要考查直线与圆的位置关系,熟练掌握直线与圆的位置关系是解题的关键.
5.C
【分析】根据圆周角定理求出∠DOB,根据等腰三角形性质求出∠OCD=∠ODC,根据三角形内角和定理求出即可.
【详解】解:连接OD,
∵∠DAB=25°,
∴∠BOD=2∠DAB=50°,
∴∠COD=90°-50°=40°,
∵OC=OD,
∴∠OCD=∠ODC=(180°-∠COD)=70°,
故选:C.
【点睛】本题考查了圆周角定理,等腰三角形性质,三角形内角和定理的应用,主要考查学生的推理能力,题目比较典型,难度适中.
6.D
【分析】由圆周角定理可求∠ACB=90°,由弧的关系得出角的关系,进而可求∠ABC=30°,∠CAB=60°,由直角三角形的性质可求∠CAH=∠ACE=30°,即可求解.
【详解】解:∵AB是直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵,
∴∠CAB=2∠ABC,
∴∠ABC=30°,∠CAB=60°,
∵CD⊥AB,
∴∠AEC=90°,
∴∠ACE=30°,
∵点H是AG的中点,∠ACB=90°,
∴AH=CH=HG,
∴∠CAH=∠ACE=30°,
∵∠CAF=∠CBF,
∴∠CBF=30°,
故选:D.
【点睛】本题考查了圆周角定理,圆心角、弧、弦的关系,直角三角形的性质,求出∠CAB的度数是本题的关键.
7.B
【分析】延长CD交⊙O于点F,连接AF,则由CD经过圆心O可得∠CAF=90°,先由翻折得到∠BCA=∠DCA,AB=AD,∠CAD=∠CAB=36°,然后得到∠FAO=54°,再由圆周角定理得到AB=AF,进而得到AF=AD,也就有∠ADF=∠AFD=63°,再由三角形的外角性质得到∠ACD的大小,最后由旋转的性质得到∠DCE的大小.
【详解】解:如图,延长CD交⊙O于点F,连接AF,
由题可知,,
垂直平分,
CD经过圆心O,
∴∠CAF=90°,
由翻折得,∠DCA=∠BCA,AB=AD,∠CAD=∠CAB=36°,
∴∠FAO=∠CAF﹣∠CAD=90°﹣36°=54°,AB=AF,
∴AF=AD,
∴∠ADF=∠AFD=(180°﹣∠DAF)=(180°﹣54°)=63°,
∵∠ADF是△ACD的外角,
∴∠ACD=∠ADF﹣∠CAD=63°﹣36°=27°,
∴∠BCA=27°,
由旋转的性质得,∠DCE=∠BCA=27°,
故选:B.
【点睛】本题考查了圆周角定理、等腰三角形的判定与性质、旋转的性质、翻折的性质、三角形的外角性质,解题的关键是熟知“直径所对的圆周角为直角”求得∠DAF的大小.
8.B
【分析】取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,利用勾股定理得到AB的长,进而可求出OC,OP的长,求得∠CMO=90°,于是得到点M在以OC为直径的圆上,然后根据圆的周长公式计算点M运动的路径长.
【详解】解:取AB的中点O、AC的中点E、BC的中点F,连接OC、OP、OM、OE、OF、EF,如图,
∵在等腰Rt△ABC中,AC=BC=2,
∴AB=BC=4,
∴OC=OP=AB=2,
∵∠ACB=90°,
∴C在⊙O上,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以OC为直径的圆上,
P点在A点时,M点在E点;P点在B点时,M点在F点.
∵O是AB中点,E是AC中点,
∴OE是△ABC的中位线,
∴OE//BC,OE=BC=,
∴OE⊥AC,
同理OF⊥BC,OF=,
∴四边形CEOF是矩形,
∵OE=OF,
∴四边形CEOF为正方形,EF=OC=2,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长=×π×2=π.
故选:B.
【点睛】本题考查了等腰三角形的性质,勾股定理,正方形的判定与性质,圆周角定理,以及动点的轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用圆周角定理确定M点的轨迹为以EF为直径的半圆.
9.A
【分析】作出等腰三角形底边上的高线OE,首先根据直角三角形30°所对的直角边等于斜边的一半求出等腰三角形底边上的高线OE的长度,即得到扇形OCD所在的圆的半径R,然后根据弧长公式求出的长度,的长度即为圆锥底面圆的周长,最后根据周长求出半径即可.
【详解】如图,过点O作OE⊥AB,垂足为E,
∵△OAB为顶角为120°的等腰三角形,
∴=30°,cm,
∴cm,
设圆锥的底面圆半径为rcm,根据题意得,
,
解得,
所以该圆锥的底面圆的半径为15cm,
故选A.
【点睛】本题考查了直角三角形30°所对的直角边等于斜边的一半、扇形的弧长公式、圆的周长公式,准确将扇形的弧长转化为底面圆的周长是解决本题的关键.
10.A
【详解】如图,连接OA,则在直角△OMA中,根据勾股定理得到OA=.
∴点A与⊙O的位置关系是:点A在⊙O内.
故选A.
11.16
【分析】连接,由垂径定理可得,在中利用勾股定理即可求得的长,进而求得.
【详解】解:连接,
∵OE⊥AB于E,
∴,
在中,,OE=6,
∴,
∴,
故答案为:
【点睛】本题考查了垂径定理和勾股定理,构造直角三角形是解题的关键.
12.55°##55度
【分析】根据圆内接四边形的性质得出∠A+∠C=180°,再求出答案即可.
【详解】解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°,
∵∠A=125°,
∴∠C=180°-125°=55°,
故答案为:55°.
【点睛】本题考查了圆内接四边形的性质和圆周角定理,能熟记圆内接四边形的对角互补是解此题的关键.
13.4
【分析】设母线长为R,可得底面周长为4π,再由圆锥的侧面积是8π,可得,即可求解.
【详解】解:设母线长为R,
∵底面半径是2,
∴底面周长=2×2π=4π,
∵圆锥的侧面积是8π,
∴,解得:R=4.
故答案为:4
【点睛】本题主要考查了求圆锥的母线长,熟记圆锥的侧面积公式是解答本题的关键,难度不大.
14.
【分析】连接CE,如图,利用平行线的性质得∠COE=∠EOB=90°,再利用勾股定理计算出OE=,利用余弦的定义得到∠OCE=60°,然后根据扇形面积公式,利用
S阴影部分=S扇形BCE S△OCE S扇形BOD进行计算即可.
【详解】解:连接CE,如图,
∵AC⊥BC,
∴∠ACB=90°,
∵AC∥OE,
∴∠COE=∠EOB=90°,
∵OC=1,CE=2,
∴OE=,cos∠OCE=,
∴∠OCE=60°,
∴S阴影部分=S扇形BCE S△OCE S扇形BOD=,
故答案为.
【点睛】本题考查了扇形面积的计算:求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.
15.5π
【分析】根据旋转的性质可以得到阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积,利用扇形的面积公式计算即可求解.
【详解】∵△AOC≌△BOD,∴阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积5π.
故答案为5π.
【点睛】本题考查了旋转的性质以及扇形的面积公式,正确理解:阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积是解题的关键.
16.0.5##
【分析】先利用等腰直角三角形的性质得到,设圆锥的底面圆的半径为r,利用弧长公式得到,然后解方程即可.
【详解】解:如图:
∵,
∴,
∵,,
∴,
设圆锥的底面圆的半径为r,
根据题意得,
解得,
即圆锥的底面圆的半径为.
故答案为:0.5
【点睛】此题考查了弧长公式,90度的圆周角所对的弦是直径,勾股定理,由90度的圆周角所对的弦是直径及勾股定理求出AB的长是解题的关键.
17.36
【分析】根据正五边形的性质可求出每个内角的度数为108°,根据等腰三角形的性质可求出∠EAC=∠DCA=72°,进而可得四边形AEDF是平行四边形,求出∠DFC的度数,再根据三角形的内角和定理求出答案即可.
【详解】解:∵正五边形ABCDE,
∴∠ABC=∠EAB==108°,AB=BC=CD=DE=AE,
∴∠ACB=∠BAC==36°,
∴∠EAC=∠DCA=108°﹣36°=72°,
∴∠DEA+∠EAC=108°+72°=180°,
∴DE∥AC,
又∵DE=AE=AF,
∴四边形AEDF是平行四边形,
∴AE∥DF,
∴∠DFC=∠EAC=72°=∠DCA,
∴∠FDC=180°﹣72°﹣72°=36°,
故答案为:36°.
【点睛】本题考查正多边形与圆,掌握正五边形的性质以及三角形的内角和定理是正确解答的前提.
18.(1),M(,);(2),(,);(3)证明见试题解析.
【详解】试题分析:(1)利用配方法把一般式转化为顶点式,然后根据二次函数的性质求出抛物线的顶点坐标;
(2)连接BC,则BC与对称轴的交点为R,此时CR+AR的值最小;先求出点A、B、C的坐标,再利用待定系数法求出直线BC的解析式,进而求出其最小值和点R的坐标;
(3)设点P坐标为(x,).根据NPAB=,列出方程,解方程得到点P坐标,再计算得出,由勾股定理的逆定理得出∠MPN=90°,然后利用切线的判定定理即可证明直线MP是⊙N的切线.
试题解析:(1)∵=,∴抛物线的解析式化为顶点式为:,顶点M的坐标是(,);
(2)∵,∴当y=0时,,解得x=1或6,∴A(1,0),B(6,0),∵x=0时,y=﹣3,∴C(0,﹣3).连接BC,则BC与对称轴x=的交点为R,连接AR,则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,最小值为BC==.设直线BC的解析式为,∵B(6,0),C(0,﹣3),∴,解得:,∴直线BC的解析式为:,令x=,得y==,∴R点坐标为(,);
(3)设点P坐标为(x,).∵A(1,0),B(6,0),∴N(,0),∴以AB为直径的⊙N的半径为AB=,∴NP=,即,移项得,,得:,整理得:,解得(与A重合,舍去),,(在对称轴的右侧,舍去),(与B重合,舍去),∴点P坐标为(2,2).∵M(,),N(,0),∴==,==, ==,∴,∴∠MPN=90°,∵点P在⊙N上,∴直线MP是⊙N的切线.
考点:1.二次函数综合题;2.最值问题;3.切线的判定;4.压轴题.
19.(1)见解析
(2)见解析
【分析】(1)根据菱形的性质可得∠APB=90°,再由90°角所对的弦为圆的直径,即可求证;
(2)延长DA交于点Q,连接PQ,则PQ即为所求,理由:连接BQ,根据AB为的直径,可得∠AQB=90°,从而得到∠BDQ+∠PBQ=90°,再由菱形的性质可得∠ABP+∠PBQ=90°,再由圆周角定理,即可求解.
(1)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,即∠APB=90°,
∵经过A,B,P三点.
∴AB为的直径;
(2)
解:如图,延长DA交于点Q,即为所求,
理由:连接BQ,
∵AB为的直径,
∴∠AQB=90°,
∴∠BDQ+∠PBQ=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD,
∴∠APB=90°,∠BDQ=∠ABP,
∴∠ABP+∠PBQ=90°,
∵∠ABP+∠BAP=90°,
∴∠BAP=∠PBQ,
∵∠BAP=∠BQP,
∴∠PBQ =∠BQP,
∴BP=PQ.
【点睛】本题主要考查了圆周角定理,菱形的性质,熟练掌握圆周角定理,菱形的性质是解题的关键.
20.(1)见解析;
(2)
【分析】(1)连接DE,根据CD和EF都是⊙O的直径得到∠DEA=∠ECF=90°,根据直角三角形的性质得到CD=AD=BD,利用等腰三角形三线合一的性质推出∠ADE=∠CDE,进而得到∠ADE=∠OED,即可得到;
(2)根据直角三角形斜边上的中线求得,勾股定理求得,由(1)可得,根据切线的性质可得,根据,代入数值,即可得到FC.
(1)
证明:连接DE,
∵CD和EF都是⊙O的直径,
∴∠DEA=∠ECF=90°,
∵D是AB的中点,
∴CD=AD=BD,
∴∠ADE=∠CDE,
∵OD=OE,
∴∠OED=∠CDE,
∴∠ADE=∠OED,
∴;
(2)
连接DF,
∵CD是⊙O的直径,
∴∠DFC=90°,
∴∠DFC=∠FCE=∠CED=90°,
∴四边形CEDF是矩形,
∴FC=DE,DE∥BC,
∴,
∴AE=CE,
∴DE是△ABC的中位线,
∴,
∵AB=2CD=5,AC=3,
∴,
∴FC=2.
是的切线,
【点睛】此题考查了圆周角定理,矩形的判定定理及性质定理,勾股定理,三角形中位线的性质,熟记圆周角定理是解题的关键.
21.(1)cm
(2)cm
【分析】(1)如图1,作交于,交于,连接,由题意知,,,在中,由勾股定理得求出的值,进而可求的值;
(2)如图2,延长交于,连接,设半径为,由题意知,由折叠和中点的性质可知,在中,由勾股定理得,即,求出满足要求的解即可.
(1)
解:如图1,作交于,交于,连接
由题意知,,
在中,由勾股定理得
∴
∴的长为.
(2)
解:如图2,延长交于,连接,设半径为
由题意知,由折叠和中点的性质可知,
在中,由勾股定理得,即
解得:,(不合题意,舍去)
∴半径的长为.
【点睛】本题考查了垂径定理,折叠的性质,勾股定理等知识.解题的关键在于对知识的熟练掌握与灵活运用.
答案第1页,共2页
同课章节目录
