2021-2022学年江苏省各地苏科版数学七年级上册6.3余角、补角、对顶角期末试题分类选编(word版 含解析)
文档属性
| 名称 | 2021-2022学年江苏省各地苏科版数学七年级上册6.3余角、补角、对顶角期末试题分类选编(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 900.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 07:30:37 | ||
图片预览




文档简介
6.3 余角、补角、对顶角
1.(2022·江苏盐城·七年级期末)若∠α=55°,则∠α的余角是( )
A.35° B.45° C.135° D.145°
2.(2022·江苏南通·七年级期末)已知∠α=35°,那么∠α的余角等于( )
A.35° B.55° C.65° D.145°
3.(2022·江苏扬州·七年级期末)若的补角是150°,则的余角是( )
A.30° B.60° C.120° D.150°
4.(2022·江苏盐城·七年级期末)一个角的余角与这个角的补角之和为130°,这个角的度数是( )
A.60° B.70° C.75° D.80°
5.(2022·江苏南通·七年级期末)一个角的度数为54°12',则这个角的补角度数等于( )
A.125°48' B.125°88' C.135°48' D.136°48'
6.(2022·江苏泰州·七年级期末)下列说法:①对顶角相等;②如果a>0、b<0,那么ab<0;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点,其中错误的是( )
A.① B.② C.③ D.④
7.(2022·江苏无锡·七年级期末)下列说法中:
①两点之间的所有连线中,线段最短;
②相等的角是对顶角;
③过一点有且只有一条直线与已知直线垂直;
④若AB=BC,则点B为线段AC的中点.
其中说法正确的个数是( )
A.1个 B.2个 C.3个 D.4个
8.(2022·江苏常州·七年级期末)一副三角尺按如图所示位置放置,为公共边,量角器中心与点重合,为刻度线.如果三角尺一边与刻度线重合,那么边与下列刻度线重合的是( )
A.刻度线 B.刻度线 C.刻度线 D.刻度线
9.(2022·江苏·苏州市振华中学校七年级期末)已知的补角比它的余角的4倍还大,则的大小是( )
A. B. C. D.
10.(2022·江苏无锡·七年级期末)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.不确定
11.(2022·江苏宿迁·七年级期末)下列说法中:①延长射线AB;②经过三点一定能画出三条直线;③如果两个角相等,那么这两个角是对顶角;④点C是直线AB上的点,如果,则点C为AB的中点.其中正确的个数是( )
A.0 B.1 C.2 D.3
12.(2022·江苏·射阳县第六中学七年级期末)已知∠α=32°,则∠α的补角为_____度.
13.(2022·江苏镇江·七年级期末)若,则的余角为______度.
14.(2022·江苏扬州·七年级期末)一个角的度数是42°36′,则它的余角的度数为_____°.(结果用度表示)
15.(2022·江苏常州·七年级期末)已知∠α=20°,则∠α的补角等于______度.
16.(2022·江苏苏州·七年级期末)已知∠A=40°,则它的补角等于___.
17.(2022·江苏南京·七年级期末)若,则的余角为_______°,的补角为_______°.
18.(2022·江苏无锡·七年级期末)已知∠1与∠2互余,∠3与∠2互余,则∠1_____∠3.(填“>”,“=”或“<”)
19.(2022·江苏常州·七年级期末)的余角是__________.
20.(2022·江苏无锡·七年级期末)68°30′的余角为_____°.
21.(2022·江苏无锡·七年级期末)已知∠A=60°,则∠A的补角是______度.
22.(2022·江苏南京·七年级期末)已知是的余角、是的补角,则比大________.
23.(2022·江苏泰州·七年级期末)一个角的余角是54°38′,则这个角的补角是_____.
24.(2022·江苏江苏·七年级期末)一个角的余角比它的补角的还少15°,则这个角的度数为______.
25.(2022·江苏南京·七年级期末)如图,直线CD经过点O,若OC平分∠AOB,则,依据是______.
26.(2022·江苏南通·七年级期末)如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为_____.
27.(2022·江苏南通·七年级期末)如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________.
28.(2022·江苏无锡·七年级期末)如图,直线AB、CD相交于点O,射线OM平分∠AOC,若∠BOD=72°,则∠BOM=_________°.
29.(2022·江苏镇江·七年级期末)如图,已知点O在直线AB上,,则______.
30.(2022·江苏江苏·七年级期末)已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD的度数为________.
31.(2022·江苏无锡·七年级期末)如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=60°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
32.(2022·江苏淮安·七年级期末)如图,已知∠AOB=90°,∠BOC=60°,OD平分∠AOC.求∠BOD的度数.
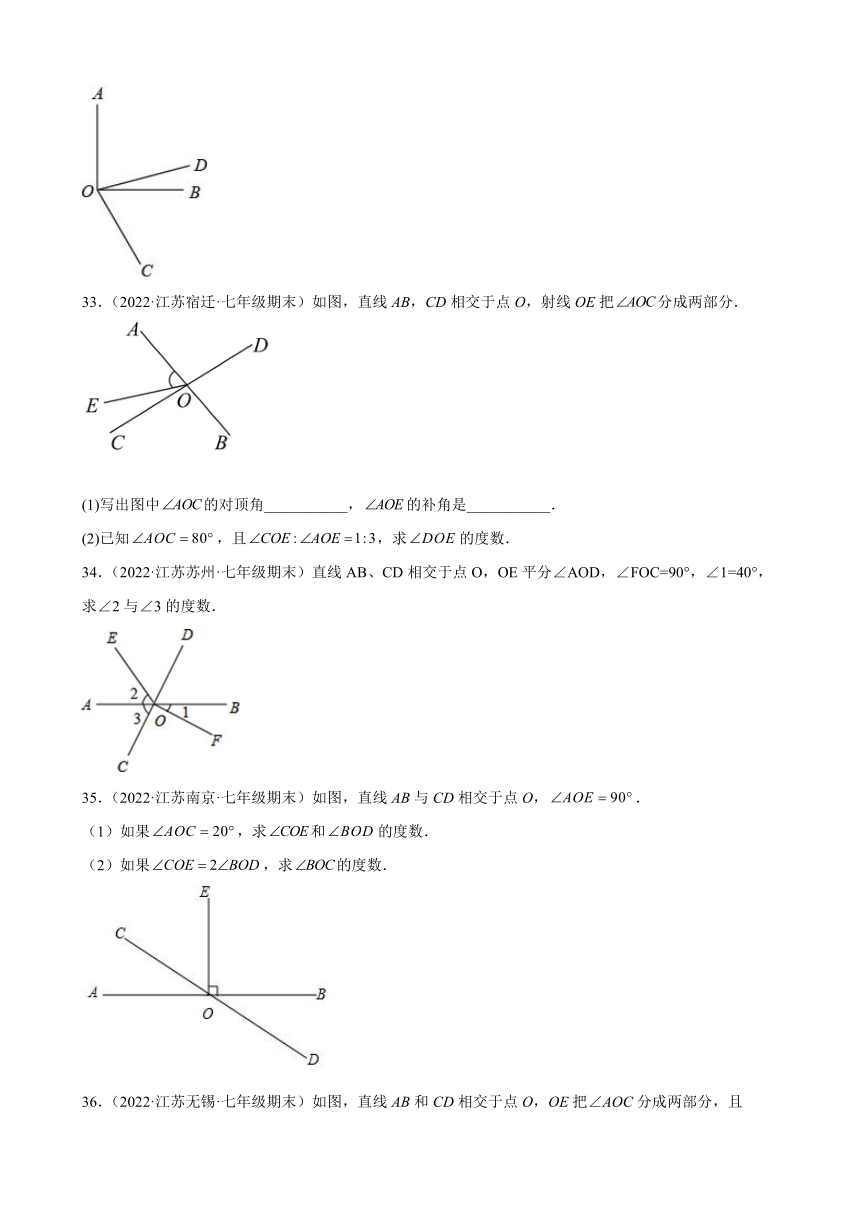
33.(2022·江苏宿迁·七年级期末)如图,直线AB,CD相交于点O,射线OE把分成两部分.
(1)写出图中的对顶角___________,的补角是___________.
(2)已知,且,求的度数.
34.(2022·江苏苏州·七年级期末)直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
35.(2022·江苏南京·七年级期末)如图,直线AB与CD相交于点O,.
(1)如果,求和的度数.
(2)如果,求的度数.
36.(2022·江苏无锡·七年级期末)如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶3,OF平分∠BOE.
(1)若∠BOD=65°,求∠BOE.
(2)若∠AOE=∠BOF﹣10°,求∠COE.
37.(2022·江苏泰州·七年级期末)如图,直线AB和CD相交于点O,若,OA平分,求的度数.
38.(2022·江苏南京·七年级期末)如图,直线AB、CD相交于点O,OE平分∠BOD,且.求∠AOC和∠DOE的度数.
39.(2022·江苏·苏州高新区实验初级中学七年级期末)直线、相交于点,平分,,,求与的度数.
40.(2022·江苏苏州·七年级期末)如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
(1)图中与∠AOF互余的角是______,与∠COE互补的角是______;(把符合条件的角都写出来)
(2)如果∠AOC=∠EOF,求∠EOF的度数.
41.(2022·江苏扬州·七年级期末)如图1,已知射线OB在∠AOC内,若满足∠BOC+∠AOC=180°,则称射线OB为∠BOC与∠AOC的“互补线”.
(1)如图2,已知点O是直线AD上一点,射线OB、OC在直线AD同侧,且射线OC平分∠BOD.试说明:射线OB为∠BOC与∠AOC的“互补线”;
(2)如图3,已知直线AB、CD相交于点O,射线OE为∠BOC与∠BOE的“互补线”,若∠AOD=136°,求∠DOE的度数;
(3)如图4,已知射线OB为∠BOC与∠AOC的“互补线”,且射线OE、OF分别平分∠AOC、∠BOC,试判断∠BOC+∠EOF的度数是否为定值,若为定值,求出定值的度数;若不为定值,请说明理由.
42.(2022·江苏扬州·七年级期末)点O为直线AB上一点,过点O作射线OC,使∠AOC=120°, 一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板DOE的一边OD与射线OB重合时,则∠COD= ∠COE;
(2)如图2,将图1中的三角板DOE绕点O逆时针旋转一定角度,当OC恰好是∠BOE的角平分线时,求∠COD的度数;
(3)将图1中的三角尺DOE绕点O逆时针旋转旋转一周,设旋转的角度为度,在旋转的过程中,能否使∠AOE=3∠COD?若能,求出的度数;若不能,说明理由.
43.(2022·江苏镇江·七年级期末)如图,点O在直线AB上,,OE是的平分线,.
(1)找出图中与相等的角,并说明理由;
(2)若,求的度数.
44.(2022·江苏江苏·七年级期末)如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间数量关系为 ;
(2)若射线OC的位置保持不变,且∠COE=130°.
①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意t的值,若不存在,请说明理由;
②如图3,在旋转的过程中,边AB与射线OE相交,请直接写出∠AOC﹣∠BOE的值.
45.(2022·江苏宿迁·七年级期末)若A、O、B三点共线,,将一个三角板的直角顶点放在点O处(注:,).
(1)如图1,使三角板的长直角边OD在射线OB上,则____________°;
(2)将图1中的三角板DOE绕点O以每秒2°的速度按逆时针方向旋转到图2位置,此时,求运动时间的值;
(3)将图2中的三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周,经过秒后,直线OC恰好平分,求的值.
46.(2022·江苏南京·七年级期末)已知与互为补角,平分.
(1)如图①,若,则______°,______°.
(2)如图②,若,求的度数;
(3)若,直接写出的度数(用含n的代数式表示),及相应的n的取值范围.
参考答案:
1.A
【解析】根据余角的定义即可得.
由余角定义得∠α的余角为90°减去55°即可.
解:由余角定义得∠α的余角等于90°﹣55°=35°.
故选:A.
本题考查了余角的定义,熟记定义是解题关键.
2.B
【解析】根据余角的定义:如果两个角的和等于90°(直角),就说这两个角互为余角计算.
解:∵∠α=35°,
∴它的余角等于90°﹣35°=55°.
故选B.
本题考查余角的概念,掌握概念正确计算是本题的解题关键.
3.B
【解析】根据补角、余角的定义即可求解.
∵的补角是150°
∴=180°-150°=30°
∴的余角是90°-30°=60°
故选B.
此题主要考查余角、补角的求解,解题的关键是熟知如果两个角的和为90度,这两个角就互为余角;补角是指如果两个角的和是一个平角,那么这两个角叫互为补角,其中一个角叫做另一个角的补角
4.B
【解析】设这个角的度数为x.再用x表示出这个角的余角和补角的度数,最后根据题意列出一元一次方程并求解即可.
解:设这个角的度数为x,则这个角的余角是,这个角的补角是.
根据题意可得90°﹣x+180°﹣x=130°,
解得:x=70°,
所以这个角是70°
故选:B.
本题考查余角的定义,补角的定义,一元一次方程的实际应用,综合应用这些知识点是解题关键.
5.A
【解析】由计算求解即可.
解:∵
∴这个角的补角度数为
故选A.
本题考查了补角.解题的关键在于明确.
6.D
【解析】根据基础几何图形的概念即可判断.
解:A、对顶角相等;此项正确;
B、如果a>0、b<0,那么ab<0;此项正确;
C、两点之间,线段最短;此项正确;
D、若AB=BC,当点B在线段AC上时,则点B是线段AC的中点;故此项错误;
故选D.
本题考查常见图形的相关概念与性质,理解并细致掌握其定义是解题的关键.
7.A
【解析】根据对顶角的定义、两点之间线段最短、线段垂直平分线的逆定理.
解:①根据两点之间,线段最短,那么①正确;
②根据对顶角的定义,对顶角一定相等,但相等的角不一定是对顶角,那么②错误;
③同一平面内,过一点有且只有一条直线与已知直线垂直,那么③错误;
④若AB=BC,则B在线段AC的垂直平分线上,即B不一定是线段AC的中点,那么④错误;
综上:正确的有①,共1个.
故选:A.
本题主要考查了对顶角、两点之间线段最短,熟练掌握对顶角的定义、两点之间线段最短是解决本题的关键.
8.A
【解析】由三角尺的特征可知,,由此即可计算出.
解:∵,,,
∴,
故选:A.
本题主要考查了三角尺中有关角的计算和角的度量,解题关键是利用余角的性质求出.
9.B
【解析】设这个角的度数为x,根据题意得180° x=4(90° x)+15°,从而解决此题.
解:设这个角的度数为x,
由题意得:180° x=4(90° x)+15°,
x=65°.
故选:B.
本题主要考查余角和补角,熟练掌握余角和补角的定义是解决本题的关键.
10.B
【解析】根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.
解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故选:B.
本题考查了余角和垂线的定义以及对顶角相等的性质.
11.A
【解析】根据直线,射线,线段和中点的定义判断对错求解.
解:①射线无限长,不可延长,故①错误.
②经过三点一定能画出1或3条直线,故②错误.
③如果两个角相等,那么这两个角是对顶角,相等的两个角不一定是对顶角,故③错误.
④点C是直线AB上的点,当点C在点A 的左侧时,也可以满足,但点C不是AB的中点.故④错误.
综上所述0个正确.
故选:A.
本题考查直线,射线,线段和中点的定义和性质,解题的关键是数量掌握基本定义及性质.
12.148
【解析】直接利用互补的定义得出答案.
解:∵∠α=32°,
∴∠α的补角为:180°﹣32°=148°.
故答案为:148.
此题主要考查了互补的定义,正确把握定义是解题的关键.
13.36.7
【解析】根据余角的定义计算即可.
解:∵=53.3°,
∴的余角=90°-53.3°
=36.7°,
故答案为:36.7.
本题考查了余角的定义,如果两个角的和等于90°那么这两个角互为余角,其中一个角叫做另一个角的余角.
14.47.4
【解析】根据余角的定义即可得到结论.
解:这个角的余角=90°-42°36′=47°24′=47.4°,
故答案为:47.4.
本题考查了余角和补角,熟记余角的定义及度分秒的换算是解题的关键.
15.160
解:∵∠α=20°,
∴∠α的补角等于180°﹣20°=160°.
故答案为160.
16.140°
【解析】根据补角的和等于计算即可.
解:,
它的补角.
故答案为.
本题考查了补角的知识,熟记互为补角的两个角的和等于是解题的关键.
17. 48°##48度 138°##138度
【解析】根据两个角的和等于90°(直角),就说这两个角互为余角,两个角的和等于180°(平角),就说这两个角互为补角,列式计算即可.
解:∠α的余角:90°-42°=48°,
∠α的补角:180°-42°=138°,
故答案为:48°、138°.
本题考查余角和补角,掌握余角和补角的定义,根据定义列式计算是解题关键.
18.=
【解析】根据等(同)角的余角相等解答即可.
解:∵∠1与∠2互余,∠3与∠2互余,
∴∠1=∠3,
故答案为:=.
本题考查余角,熟知同(等)角的余角相等是解答的关键.
19.
【解析】根据余角的定义即可求解.
的余角是90°-=
故答案为:.
此题主要考查余角的求解,解题的关键是熟知余角的定义与性质.
20.21.5
【解析】利用90°减去68°30′,然后再把单位化成度即可.
解:90°﹣68°30′=21°30′=21.5°.
故答案为:21.5.
本题考查了余角的定义及角度单位的换算,掌握定义及单位换算标准是关键.1°=60′.
21.120
【解析】两角互余和为90°,互补和为180°,求∠A的补角只要用180°﹣∠A即可.
解:设∠A的补角为∠β,则∠β=180°﹣∠A=120°.
故答案为:120.
此题主要考查补角的定义,解题的关键是熟知两角互补和为180°.
22.
【解析】先根据余角性质得出∠2=90°-∠1,再根据补角性质得出∠3=180°-∠1,根据两角差计算即可.
解∵是的余角,
∴∠2+∠1=90°,
∴∠2=90°-∠1,
∵是的补角,
∴∠3+∠1=180°,
∴∠3=180°-∠1,
∴∠3-∠2=180°-∠1-(90°-∠1)=90°.
故答案为:90.
本题考查余角性质,补角性质,角的和差,掌握余角性质,补角性质,角的和差是解题关键.
23.144°38′
【解析】根据余角是两个角的和为90°,这两个角互为余角,两个角的和为180°,这两个角互为补角,可得答案.
解:∵一个角的余角是54°38′
∴这个角为:90°﹣54°38′=35°22′,
∴这个角的补角为:180°﹣35°22′=144°38′.
故答案为144°38′.
24.30°##30度
【解析】根据互为余角和互为补角的定义得出等式进而得出答案.
解:设这个角度为x,则
90°﹣x=(180°﹣x)﹣15°,
解得:x=30°.
故答案为:30°.
本题主要考查了余角和补角的定义,正确得出等式是解题关键.
25.等角的补角相等
【解析】根据角平分线的定义和等角的补角相等解答即可.
解:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵∠AOC+∠AOD=180°,∠BOC+∠BOD=180°,
∴∠AOD=∠BOD(等角的补角相等),
故答案为:等角的补角相等.
本题考查角平分线的定义、补角,熟知等角的补角相等是解答的关键.
26.
【解析】由题意易得∠AOC=∠EOC=90°,则有∠1+∠DOE=90°,∠AOB+∠DOE=90°,进而可得∠AOB=∠1,然后问题可求解.
解:∵OC平分∠AOE,∠AOE=180°,
∴∠AOC=∠EOC=90°,
∴∠1+∠DOE=90°,
∵∠DOB=90°,
∴∠AOB+∠DOE=90°,
∴∠AOB=∠1,
∵∠1=25°,
∴∠AOB=25°,
故答案为25°.
本题主要考查余角及角平分线的定义,熟练掌握同角的余角相等及角平分线的定义是解题的关键.
27.5或23##23或5
【解析】分两种情况进行讨论,分别依据直线ON恰好平分锐角∠AOC,得到三角板旋转的度数,进而得到t的值.
解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON=∠AOC=40°,
此时,三角板旋转的角度为90°-40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°-90°-40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故答案为:5或23.
本题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
28.144
【解析】首先根据邻补角互补,对顶角相等可得∠AOC=72°,∠BOC=108°,再根据角平分线的性质可得∠MOC的度数,进而可得答案.
解:∵∠BOD=72°,
∴∠AOC=72°,∠BOC=108°,
∵OM平分∠AOC,
∴∠MOC=36°,
∴∠BOM=∠BOC+∠MOC=144°.
故答案为:144.
本题主要考查了对顶角和邻补角,角平分线的定义,关键是掌握邻补角互补,对顶角相等.
29.30°##30度
【解析】根据邻补角性质,可得∠AOC+∠BOC=180°,结合已知∠AOC=5∠BOC,解方程可求∠BOC.
解:∵∠AOC与∠BOC互为邻补角,
∴∠AOC+∠BOC=180°,①
又∵∠AOC=5∠BOC,②
把②代入①,可得5∠BOC+∠BOC=180°,
解得∠BOC=30°.
故答案为:30°.
此题考查的是角的计算,能够根据邻补角的定义列出方程是解决此题关键.
30.36°
【解析】先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,根据角平分线定义得到∠AOC∠EOC72°=36°,然后根据对顶角相等得到∠BOD=∠AOC=36°.
解:设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∵OA平分∠EOC,
∴∠AOC∠EOC72°=36°,
∴∠BOD=∠AOC=36°.
故答案为:36°
考查了角的计算,角平分线的定义和对顶角的性质.解题的关键是明确:直角=90°;平角=180°,以及对顶角相等.
31.(1)∠DOE=120°;
(2)∠AOF=45°.
【解析】(1)根据角平分线的定义,得出∠EOC=∠BOE=60°,利用邻补角定义求出∠DOE即可;
(2)根据角平分线的定义,∠BOD:∠BOE=2:3,求出∠BOD,再根据对顶角可求出∠AOC,利用垂直,求出∠AOF.
(1)
解:∵OE平分∠BOC,∠BOE=60°,
∴∠EOC=∠BOE=60°,
∴∠DOE=180°-60°=120°;
(2)
解:∵∠BOD:∠BOE=2:3,
设∠BOD=x,则∠COE=∠BOE=x,
∵∠COE+∠BOE+∠BOD=180°,
∴x+x+x=180°,
∴x=45°,即∠BOD=45°,
∵OF⊥CD,∠AOC=∠BOD=45°,
∴∠COF=90°,
∴∠AOF=90°-45°=45°.
本题考查了角平分线定义,邻补角定义,对顶角性质,垂直定义,角的计算等;正确找出各个角之间的关系是正确计算的关键.
32.∠BOD=15°.
【解析】本题需先结合图形,得出∠AOC的度数,再根据OD平分∠AOC,得出∠AOD的度数,最后即可求出正确答案.
解:∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=150°.
∵OD平分∠AOC,
∴∠AOD=∠COD=∠AOC=75°,
∴∠BOD=∠AOB-∠AOD=15°.
本题主要考查了角平分线定义的应用以及角的计算.利用图形计算角的和差是解题的关键.
33.(1),
(2)160°
【解析】(1)根据对顶角和补角的定义,即可求解;
(2)根据,可得,从而得到,即可求解.
(1)
解:根据题意得:的对顶角为;
的补角是,
故答案为:,;
(2)
解:∵,,
∴,
∵,
∴,
∵,
∴.
本题主要考查了对顶角和补角的定义,角的和与差,邻补角的性质,熟练掌握对顶角和补角的定义,邻补角的性质是解题的关键.
34.∠3=50°,∠2=65°.
【解析】根据平角为180度可得∠3=180°-∠1-∠FOC ,根据对顶角相等可得∠AOD的度数,然后再根据角平分线定义进行计算即可
解:∵∠AOB=180°,
∴∠1+∠3+∠COF=180°,
∵∠FOC=90°,∠1=40°,
∴∠3=180°-∠1-∠FOC=50°, ∠BOC=∠1+∠FOC=130°,
∴∠AOD=∠BOC=130°,
∵OE平分∠AOD,
∴∠2=∠AOD=65°.
本题主要考查了对顶角,邻补角性质,角平分线的定义,掌握以上知识是解题的关键.
35.(1)70°,20°;(2)150°
【解析】(1)根据题意及余角、对顶角的意义可直接进行求解;
(2)设,则,则有,进而根据角的和差关系可求解.
解:(1),,
,;
(2)设,则,
,
即,
解得,,
,
.
本题主要考查余补角、对顶角的意义及一元一次方程的应用,熟练掌握余补角、对顶角的意义及一元一次方程的应用是解题的关键.
36.(1)∠BOE=154°;
(2)∠COE=42°.
【解析】(1)根据对顶角的定义,由∠AOC与∠BOD是对顶角,得∠AOC=∠BOD=65°.由∠AOE:∠EOC=2:3,求得∠AOE=∠AOC=26°.根据邻补角的定义,得∠BOE=180°-∠AOE=154°.
(2)设∠AOE=2x,∠EOC=3x.由∠AOE=∠BOF-10°,得∠BOF=4x+20°.根据角平分线的定义,由OF平分∠BOE,得∠BOE=2∠BOF=8x+40°.根据邻补角的定义,得∠AOE+∠BOE=2x+8x+40°=180°,进而解决此题.
(1)
解:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=65°.
∵∠AOE:∠EOC=2:3,
∴∠AOE=∠AOC=26°.
∴∠BOE=180°-∠AOE=180°-26°=154°;
(2)
解:设∠AOE=2x,∠EOC=3x.
∵∠AOE=∠BOF-10°,
∴∠BOF=4x+20°.
∵OF平分∠BOE,
∴∠BOE=2∠BOF=8x+40°.
∴∠AOE+∠BOE=2x+8x+40°=180°.
∴x=14°.
∴∠COE=3x=42°.
本题主要考查了对顶角、邻补角、角平分线,熟练掌握对顶角、邻补角、角平分线的定义是解决本题的关键.
37.100°
【解析】根据对顶角相等以及角平分线的性质可得出∠AOE的度数,再根据平角的定义即可得出∠EOD的度数.
解:∵∠BOD=40°,
∴∠AOC=∠BOD=40°.
∵OA平分∠EOC,
∴∠AOE=∠AOC=40°,
∴.
本题主要考查了角平分线的性质以及对顶角、邻补角的性质,难度不大.
38.50°,25°.
【解析】根据邻补角的性质,可得∠AOD+∠BOD=180°,即,代入可得∠BOD,根据对顶角的性质,可得∠∠AOC的度数,根据角平分线的性质,可得∠DOE的数.
解:由邻补角的性质,得∠AOD+∠BOD=180°,即
∵,
∴.
∴,
∴∠AOC=∠BOD=50°,
∵OE平分∠BOD,得
∠DOE=∠DOB=25°.
本题考查了角平分线的定义,对顶角、邻补角的性质,解题关键是熟记相关性质,根据角之间的关系建立方程求解.
39.∠3=50°,∠2=65°.
【解析】根据邻补角的性质、角平分线的定义进行解答即可.
∵∠FOC=90°,∠1=40°,
∴∠3=180°-∠FOC-∠1 =180°-90°-40°=50°,
∴∠AOD=180°-∠3=180°-50°=130°,
又∵OE平分∠AOD,
∴∠2=∠AOD=65°.
本题考查的是邻补角的概念和性质、角平分线的定义,掌握邻补角之和等于180°是解题的关键.
40.(1)∠AOC、∠BOD;∠EOD、∠BOF;(2)∠EOF=144°.
【解析】(1)根据互余及互补的定义,结合图形进行判断即可;
(2)设∠AOC=x,则∠BOD=x,∠EOF=4x,根据周角为360度,即可解出x.
解:(1)图中与∠AOF互余的角是:∠AOC、∠BOD;
图中与∠COE互补的角是:∠EOD、∠BOF.
(2)∵OE⊥AB,OF⊥CD,
∴∠EOB=90°,∠FOD=90°,
又∵∠AOC=∠EOF,
设∠AOC=x,则∠BOD=x,∠EOF=4x,
根据题意可得:4x+x+90+90=360°,
解得:x=36°.
∴∠EOF=4x=144°.
本题考查了余角和补角的知识,注意结合图形进行求解.
41.(1)见解析
(2)
(3)
【解析】(1)根据定义直接求解即可;
(2)根据等角的补角相等可得,进而根据邻补角的定义求得,根据对顶角相等可得,进而根据角的和求解即可;
(3)根据角平分线的意义,以及角度的和差计算可得,即可求得答案.
(1)证明:OC平分∠BOD射线OB为∠BOC与∠AOC的“互补线”
(2)射线OE为∠BOC与∠BOE的“互补线”,
(3)射线OB为∠BOC与∠AOC的“互补线”,射线OE、OF分别平分∠AOC、∠BOC,
本题考查了新定义,等角的补角相等,根据邻补角求角度,角平分线的意义,几何图形中角度的和差关系,理解题意,数形结合是解题的关键.
42.(1)2
(2)
(3)或
【解析】(1)由邻补角和余角的定义求出两个角,即可得出结论;
(2)由角平分线的定义可得,再根据,从而可求解;
(3)分两种情况讨论:①是内;②在外,分析清楚角关系求解即可.
(1)
解:,与射线重合,
,
,
,
,
故答案为:2;
(2)
解:由(1)得,,
是的角平分线,
,
,
;
(3)
解:能,
①当是内时,有:
,,
则,
解得:;
②当在外时,有:
,,
则,
解得:.
综上所述,的度数为或.
本题主要考查三角形的内角和定理,余角和补角,解题的关键是结合图形分析清楚角与角之间的关系.
43.(1),理由见解析;(2)
【解析】(1)利用垂直的定义以及同角的余角相等可得出∠COE=∠BOF;
(2)通过垂直的定义得到∠COA=90°,再由已知∠2-∠1=20°,得到∠1、∠2的值,然后由角平分线的定义得出结果.
解:(1)∵CO⊥AB,OF⊥OE,
∴∠COE+∠BOE=∠BOE+∠BOF=90°
∴∠COE=∠BOF;
(2)∵CO⊥AB,
∴∠COA=90°,即∠2=90°-∠1,
又∵∠2-∠1=20°,
∴∠2=20°+∠1,
∴90°-∠1=20°+∠1,
解得:∠1=35°,
∴∠2=55°,
∴∠BOD=180°-∠2=125°,
∵OE是∠BOD的平分线,
∴∠BOE=∠DOE=∠BOD=62.5°.
本题考查垂直和角平分线的定义,同角的余角相等,掌 握相关概念正确推理计算是解题关键.
44.(1)∠BOC=∠BOE.
(2)①存在,t=2.5或10或31;②40°
【解析】(1)由∠AOB=90°知∠BOC+∠AOC=90°、∠AOD+∠BOE=90°,根据∠AOD=∠AOC可得答案;
(2)①当OA平分∠COD时∠AOD=∠AOC、当OC平分∠AOD时∠AOC=∠COD、当OD平分∠AOC时∠AOD=∠COD,分别列出关于t的方程,解之可得;
②根据角的和差即可得到结论.
(1)
解:∠BOC=∠BOE.
理由如下:
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,∠AOD+∠BOE=90°,
∵OA平分∠COD,
∴∠AOD=∠AOC,
∴∠BOC=∠BOE,
故答案为:∠BOC=∠BOE;
(2)
①存在.
理由:∵∠COE=130°,
∴∠COD=180°﹣130°=50°,
当OA平分∠COD时,∠AOD=∠AOC=∠COD,即10t=25,解得t=2.5;
当OC平分∠AOD时,∠AOC=∠COD,即10t﹣50=50,解得t=10;
当OD平分∠AOC时,∠AOD=∠COD,即360﹣10t=50,解得:t=31;
综上所述,t的值为2.5、10、31;
②∵∠AOC=∠COE﹣∠AOE=130°﹣∠AOE,∠BOE=90°﹣∠AOE,
∴∠AOC﹣∠BOE=(130°﹣∠AOE)﹣(90°﹣∠AOE)=40°,
∴∠AOC﹣∠BOE的值为40°.
本题主要考查角平分线的定义、余角的性质及角的计算,根据题意全面考虑所有可能以分类讨论是解题的关键.
45.(1)50
(2)25秒
(3)11或47
【解析】(1)由余角的性质可求解;
(2)由角的数量关系列出等式可求解;
(3)分两种情况讨论即可.
(1)
解:∵∠DOE=90°,∠BOC=40°,
∴∠COE=∠DOE-∠BOC=90°-40°=50°,
故答案为:50;
(2)
解:∵三角板DOE绕点O以每秒2°的速度按逆时针方向旋转,
∴经过t秒,∠COD=∠BOD-∠BOC=2t-40 ,∠AOE=90 -2t,
∵,
∴2t-40 =(90 -2t),
解得t=25.
即运动时间为25秒.
(3)
解:图2中∠AOE=90 -2t=40 ,∠D1O E1=∠DOE=90
∵三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周,
情况①如图:
经过秒后,∠EOE1=5t
∵直线OC恰好平分,
∴
∵∠BOC=40
∠AOC=∠AOE+∠EOE1+=140
即40 +5t+45 =140
解得:t=11;
情况②如图:
此时有:5t-10 -45 =180 ,
解得t=47
故的值为11或47.
本题考查了一元一次方程的应用,角平分线的定义,平角的性质等知识,熟练运用这些性质解决问题是本题的关键.
46.(1),
(2)或
(3)答案见解析
【解析】(1)根据补角的定义可求度数,在利用角平分线的定义可求解度数,进而求解的度数;
(2)分两种情况:当在的外部时,当在的内部时,利用补角的定义结合角平分线的定义可求解;
(3)可分两种情况:当和互为邻补角时,即和在的不同侧时;当和在的同一侧时。而对于当和在的同一侧时可分为:当 时;当时;当时分别计算求解即可.
(1)
解:与互为补角,
,
,
平分,
,
,
故答案为:,;
(2)
解:当在的外部时,
与互为补角,
,
平分,
,
,
当在的内部时,
与互为补角,
,
平分,
,
,
的度数为或;
(3)
当和互为邻补角时,即和在的不同侧时,
,
,
平分,
,
,
即此时;
当和在的同一侧时,
当,如图,此时,,
平分,
,和重合,
;
当时,如图,
,,
平分,
,
,
,
即,此时,
当,如图,,,
平分,
,
,
即,此时,
综上,当和在的不同侧时,
,此时;
当和在的同一侧时,
当时,;
当时,;
当时,.
本题主要考查角的计算,三角形的外角定义,角平分线的性质,分类讨论是解决问题的关键.
1.(2022·江苏盐城·七年级期末)若∠α=55°,则∠α的余角是( )
A.35° B.45° C.135° D.145°
2.(2022·江苏南通·七年级期末)已知∠α=35°,那么∠α的余角等于( )
A.35° B.55° C.65° D.145°
3.(2022·江苏扬州·七年级期末)若的补角是150°,则的余角是( )
A.30° B.60° C.120° D.150°
4.(2022·江苏盐城·七年级期末)一个角的余角与这个角的补角之和为130°,这个角的度数是( )
A.60° B.70° C.75° D.80°
5.(2022·江苏南通·七年级期末)一个角的度数为54°12',则这个角的补角度数等于( )
A.125°48' B.125°88' C.135°48' D.136°48'
6.(2022·江苏泰州·七年级期末)下列说法:①对顶角相等;②如果a>0、b<0,那么ab<0;③两点之间,线段最短;④若AB=BC,则点B是线段AC的中点,其中错误的是( )
A.① B.② C.③ D.④
7.(2022·江苏无锡·七年级期末)下列说法中:
①两点之间的所有连线中,线段最短;
②相等的角是对顶角;
③过一点有且只有一条直线与已知直线垂直;
④若AB=BC,则点B为线段AC的中点.
其中说法正确的个数是( )
A.1个 B.2个 C.3个 D.4个
8.(2022·江苏常州·七年级期末)一副三角尺按如图所示位置放置,为公共边,量角器中心与点重合,为刻度线.如果三角尺一边与刻度线重合,那么边与下列刻度线重合的是( )
A.刻度线 B.刻度线 C.刻度线 D.刻度线
9.(2022·江苏·苏州市振华中学校七年级期末)已知的补角比它的余角的4倍还大,则的大小是( )
A. B. C. D.
10.(2022·江苏无锡·七年级期末)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.不确定
11.(2022·江苏宿迁·七年级期末)下列说法中:①延长射线AB;②经过三点一定能画出三条直线;③如果两个角相等,那么这两个角是对顶角;④点C是直线AB上的点,如果,则点C为AB的中点.其中正确的个数是( )
A.0 B.1 C.2 D.3
12.(2022·江苏·射阳县第六中学七年级期末)已知∠α=32°,则∠α的补角为_____度.
13.(2022·江苏镇江·七年级期末)若,则的余角为______度.
14.(2022·江苏扬州·七年级期末)一个角的度数是42°36′,则它的余角的度数为_____°.(结果用度表示)
15.(2022·江苏常州·七年级期末)已知∠α=20°,则∠α的补角等于______度.
16.(2022·江苏苏州·七年级期末)已知∠A=40°,则它的补角等于___.
17.(2022·江苏南京·七年级期末)若,则的余角为_______°,的补角为_______°.
18.(2022·江苏无锡·七年级期末)已知∠1与∠2互余,∠3与∠2互余,则∠1_____∠3.(填“>”,“=”或“<”)
19.(2022·江苏常州·七年级期末)的余角是__________.
20.(2022·江苏无锡·七年级期末)68°30′的余角为_____°.
21.(2022·江苏无锡·七年级期末)已知∠A=60°,则∠A的补角是______度.
22.(2022·江苏南京·七年级期末)已知是的余角、是的补角,则比大________.
23.(2022·江苏泰州·七年级期末)一个角的余角是54°38′,则这个角的补角是_____.
24.(2022·江苏江苏·七年级期末)一个角的余角比它的补角的还少15°,则这个角的度数为______.
25.(2022·江苏南京·七年级期末)如图,直线CD经过点O,若OC平分∠AOB,则,依据是______.
26.(2022·江苏南通·七年级期末)如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为_____.
27.(2022·江苏南通·七年级期末)如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________.
28.(2022·江苏无锡·七年级期末)如图,直线AB、CD相交于点O,射线OM平分∠AOC,若∠BOD=72°,则∠BOM=_________°.
29.(2022·江苏镇江·七年级期末)如图,已知点O在直线AB上,,则______.
30.(2022·江苏江苏·七年级期末)已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD的度数为________.
31.(2022·江苏无锡·七年级期末)如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=60°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
32.(2022·江苏淮安·七年级期末)如图,已知∠AOB=90°,∠BOC=60°,OD平分∠AOC.求∠BOD的度数.
33.(2022·江苏宿迁·七年级期末)如图,直线AB,CD相交于点O,射线OE把分成两部分.
(1)写出图中的对顶角___________,的补角是___________.
(2)已知,且,求的度数.
34.(2022·江苏苏州·七年级期末)直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2与∠3的度数.
35.(2022·江苏南京·七年级期末)如图,直线AB与CD相交于点O,.
(1)如果,求和的度数.
(2)如果,求的度数.
36.(2022·江苏无锡·七年级期末)如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶3,OF平分∠BOE.
(1)若∠BOD=65°,求∠BOE.
(2)若∠AOE=∠BOF﹣10°,求∠COE.
37.(2022·江苏泰州·七年级期末)如图,直线AB和CD相交于点O,若,OA平分,求的度数.
38.(2022·江苏南京·七年级期末)如图,直线AB、CD相交于点O,OE平分∠BOD,且.求∠AOC和∠DOE的度数.
39.(2022·江苏·苏州高新区实验初级中学七年级期末)直线、相交于点,平分,,,求与的度数.
40.(2022·江苏苏州·七年级期末)如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
(1)图中与∠AOF互余的角是______,与∠COE互补的角是______;(把符合条件的角都写出来)
(2)如果∠AOC=∠EOF,求∠EOF的度数.
41.(2022·江苏扬州·七年级期末)如图1,已知射线OB在∠AOC内,若满足∠BOC+∠AOC=180°,则称射线OB为∠BOC与∠AOC的“互补线”.
(1)如图2,已知点O是直线AD上一点,射线OB、OC在直线AD同侧,且射线OC平分∠BOD.试说明:射线OB为∠BOC与∠AOC的“互补线”;
(2)如图3,已知直线AB、CD相交于点O,射线OE为∠BOC与∠BOE的“互补线”,若∠AOD=136°,求∠DOE的度数;
(3)如图4,已知射线OB为∠BOC与∠AOC的“互补线”,且射线OE、OF分别平分∠AOC、∠BOC,试判断∠BOC+∠EOF的度数是否为定值,若为定值,求出定值的度数;若不为定值,请说明理由.
42.(2022·江苏扬州·七年级期末)点O为直线AB上一点,过点O作射线OC,使∠AOC=120°, 一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板DOE的一边OD与射线OB重合时,则∠COD= ∠COE;
(2)如图2,将图1中的三角板DOE绕点O逆时针旋转一定角度,当OC恰好是∠BOE的角平分线时,求∠COD的度数;
(3)将图1中的三角尺DOE绕点O逆时针旋转旋转一周,设旋转的角度为度,在旋转的过程中,能否使∠AOE=3∠COD?若能,求出的度数;若不能,说明理由.
43.(2022·江苏镇江·七年级期末)如图,点O在直线AB上,,OE是的平分线,.
(1)找出图中与相等的角,并说明理由;
(2)若,求的度数.
44.(2022·江苏江苏·七年级期末)如图1,直线DE上有一点O,过点O在直线DE上方作射线OC,将一直角三角板AOB(其中∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕着点O按每秒10°的速度逆时针旋转一周,设旋转时间为t秒.
(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间数量关系为 ;
(2)若射线OC的位置保持不变,且∠COE=130°.
①在旋转的过程中,是否存在某个时刻,使得射线OA,OC,OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意t的值,若不存在,请说明理由;
②如图3,在旋转的过程中,边AB与射线OE相交,请直接写出∠AOC﹣∠BOE的值.
45.(2022·江苏宿迁·七年级期末)若A、O、B三点共线,,将一个三角板的直角顶点放在点O处(注:,).
(1)如图1,使三角板的长直角边OD在射线OB上,则____________°;
(2)将图1中的三角板DOE绕点O以每秒2°的速度按逆时针方向旋转到图2位置,此时,求运动时间的值;
(3)将图2中的三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周,经过秒后,直线OC恰好平分,求的值.
46.(2022·江苏南京·七年级期末)已知与互为补角,平分.
(1)如图①,若,则______°,______°.
(2)如图②,若,求的度数;
(3)若,直接写出的度数(用含n的代数式表示),及相应的n的取值范围.
参考答案:
1.A
【解析】根据余角的定义即可得.
由余角定义得∠α的余角为90°减去55°即可.
解:由余角定义得∠α的余角等于90°﹣55°=35°.
故选:A.
本题考查了余角的定义,熟记定义是解题关键.
2.B
【解析】根据余角的定义:如果两个角的和等于90°(直角),就说这两个角互为余角计算.
解:∵∠α=35°,
∴它的余角等于90°﹣35°=55°.
故选B.
本题考查余角的概念,掌握概念正确计算是本题的解题关键.
3.B
【解析】根据补角、余角的定义即可求解.
∵的补角是150°
∴=180°-150°=30°
∴的余角是90°-30°=60°
故选B.
此题主要考查余角、补角的求解,解题的关键是熟知如果两个角的和为90度,这两个角就互为余角;补角是指如果两个角的和是一个平角,那么这两个角叫互为补角,其中一个角叫做另一个角的补角
4.B
【解析】设这个角的度数为x.再用x表示出这个角的余角和补角的度数,最后根据题意列出一元一次方程并求解即可.
解:设这个角的度数为x,则这个角的余角是,这个角的补角是.
根据题意可得90°﹣x+180°﹣x=130°,
解得:x=70°,
所以这个角是70°
故选:B.
本题考查余角的定义,补角的定义,一元一次方程的实际应用,综合应用这些知识点是解题关键.
5.A
【解析】由计算求解即可.
解:∵
∴这个角的补角度数为
故选A.
本题考查了补角.解题的关键在于明确.
6.D
【解析】根据基础几何图形的概念即可判断.
解:A、对顶角相等;此项正确;
B、如果a>0、b<0,那么ab<0;此项正确;
C、两点之间,线段最短;此项正确;
D、若AB=BC,当点B在线段AC上时,则点B是线段AC的中点;故此项错误;
故选D.
本题考查常见图形的相关概念与性质,理解并细致掌握其定义是解题的关键.
7.A
【解析】根据对顶角的定义、两点之间线段最短、线段垂直平分线的逆定理.
解:①根据两点之间,线段最短,那么①正确;
②根据对顶角的定义,对顶角一定相等,但相等的角不一定是对顶角,那么②错误;
③同一平面内,过一点有且只有一条直线与已知直线垂直,那么③错误;
④若AB=BC,则B在线段AC的垂直平分线上,即B不一定是线段AC的中点,那么④错误;
综上:正确的有①,共1个.
故选:A.
本题主要考查了对顶角、两点之间线段最短,熟练掌握对顶角的定义、两点之间线段最短是解决本题的关键.
8.A
【解析】由三角尺的特征可知,,由此即可计算出.
解:∵,,,
∴,
故选:A.
本题主要考查了三角尺中有关角的计算和角的度量,解题关键是利用余角的性质求出.
9.B
【解析】设这个角的度数为x,根据题意得180° x=4(90° x)+15°,从而解决此题.
解:设这个角的度数为x,
由题意得:180° x=4(90° x)+15°,
x=65°.
故选:B.
本题主要考查余角和补角,熟练掌握余角和补角的定义是解决本题的关键.
10.B
【解析】根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.
解:图中,∠2=∠COE(对顶角相等),
又∵AB⊥CD,
∴∠1+∠COE=90°,
∴∠1+∠2=90°,
∴两角互余.
故选:B.
本题考查了余角和垂线的定义以及对顶角相等的性质.
11.A
【解析】根据直线,射线,线段和中点的定义判断对错求解.
解:①射线无限长,不可延长,故①错误.
②经过三点一定能画出1或3条直线,故②错误.
③如果两个角相等,那么这两个角是对顶角,相等的两个角不一定是对顶角,故③错误.
④点C是直线AB上的点,当点C在点A 的左侧时,也可以满足,但点C不是AB的中点.故④错误.
综上所述0个正确.
故选:A.
本题考查直线,射线,线段和中点的定义和性质,解题的关键是数量掌握基本定义及性质.
12.148
【解析】直接利用互补的定义得出答案.
解:∵∠α=32°,
∴∠α的补角为:180°﹣32°=148°.
故答案为:148.
此题主要考查了互补的定义,正确把握定义是解题的关键.
13.36.7
【解析】根据余角的定义计算即可.
解:∵=53.3°,
∴的余角=90°-53.3°
=36.7°,
故答案为:36.7.
本题考查了余角的定义,如果两个角的和等于90°那么这两个角互为余角,其中一个角叫做另一个角的余角.
14.47.4
【解析】根据余角的定义即可得到结论.
解:这个角的余角=90°-42°36′=47°24′=47.4°,
故答案为:47.4.
本题考查了余角和补角,熟记余角的定义及度分秒的换算是解题的关键.
15.160
解:∵∠α=20°,
∴∠α的补角等于180°﹣20°=160°.
故答案为160.
16.140°
【解析】根据补角的和等于计算即可.
解:,
它的补角.
故答案为.
本题考查了补角的知识,熟记互为补角的两个角的和等于是解题的关键.
17. 48°##48度 138°##138度
【解析】根据两个角的和等于90°(直角),就说这两个角互为余角,两个角的和等于180°(平角),就说这两个角互为补角,列式计算即可.
解:∠α的余角:90°-42°=48°,
∠α的补角:180°-42°=138°,
故答案为:48°、138°.
本题考查余角和补角,掌握余角和补角的定义,根据定义列式计算是解题关键.
18.=
【解析】根据等(同)角的余角相等解答即可.
解:∵∠1与∠2互余,∠3与∠2互余,
∴∠1=∠3,
故答案为:=.
本题考查余角,熟知同(等)角的余角相等是解答的关键.
19.
【解析】根据余角的定义即可求解.
的余角是90°-=
故答案为:.
此题主要考查余角的求解,解题的关键是熟知余角的定义与性质.
20.21.5
【解析】利用90°减去68°30′,然后再把单位化成度即可.
解:90°﹣68°30′=21°30′=21.5°.
故答案为:21.5.
本题考查了余角的定义及角度单位的换算,掌握定义及单位换算标准是关键.1°=60′.
21.120
【解析】两角互余和为90°,互补和为180°,求∠A的补角只要用180°﹣∠A即可.
解:设∠A的补角为∠β,则∠β=180°﹣∠A=120°.
故答案为:120.
此题主要考查补角的定义,解题的关键是熟知两角互补和为180°.
22.
【解析】先根据余角性质得出∠2=90°-∠1,再根据补角性质得出∠3=180°-∠1,根据两角差计算即可.
解∵是的余角,
∴∠2+∠1=90°,
∴∠2=90°-∠1,
∵是的补角,
∴∠3+∠1=180°,
∴∠3=180°-∠1,
∴∠3-∠2=180°-∠1-(90°-∠1)=90°.
故答案为:90.
本题考查余角性质,补角性质,角的和差,掌握余角性质,补角性质,角的和差是解题关键.
23.144°38′
【解析】根据余角是两个角的和为90°,这两个角互为余角,两个角的和为180°,这两个角互为补角,可得答案.
解:∵一个角的余角是54°38′
∴这个角为:90°﹣54°38′=35°22′,
∴这个角的补角为:180°﹣35°22′=144°38′.
故答案为144°38′.
24.30°##30度
【解析】根据互为余角和互为补角的定义得出等式进而得出答案.
解:设这个角度为x,则
90°﹣x=(180°﹣x)﹣15°,
解得:x=30°.
故答案为:30°.
本题主要考查了余角和补角的定义,正确得出等式是解题关键.
25.等角的补角相等
【解析】根据角平分线的定义和等角的补角相等解答即可.
解:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵∠AOC+∠AOD=180°,∠BOC+∠BOD=180°,
∴∠AOD=∠BOD(等角的补角相等),
故答案为:等角的补角相等.
本题考查角平分线的定义、补角,熟知等角的补角相等是解答的关键.
26.
【解析】由题意易得∠AOC=∠EOC=90°,则有∠1+∠DOE=90°,∠AOB+∠DOE=90°,进而可得∠AOB=∠1,然后问题可求解.
解:∵OC平分∠AOE,∠AOE=180°,
∴∠AOC=∠EOC=90°,
∴∠1+∠DOE=90°,
∵∠DOB=90°,
∴∠AOB+∠DOE=90°,
∴∠AOB=∠1,
∵∠1=25°,
∴∠AOB=25°,
故答案为25°.
本题主要考查余角及角平分线的定义,熟练掌握同角的余角相等及角平分线的定义是解题的关键.
27.5或23##23或5
【解析】分两种情况进行讨论,分别依据直线ON恰好平分锐角∠AOC,得到三角板旋转的度数,进而得到t的值.
解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON=∠AOC=40°,
此时,三角板旋转的角度为90°-40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°-90°-40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故答案为:5或23.
本题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
28.144
【解析】首先根据邻补角互补,对顶角相等可得∠AOC=72°,∠BOC=108°,再根据角平分线的性质可得∠MOC的度数,进而可得答案.
解:∵∠BOD=72°,
∴∠AOC=72°,∠BOC=108°,
∵OM平分∠AOC,
∴∠MOC=36°,
∴∠BOM=∠BOC+∠MOC=144°.
故答案为:144.
本题主要考查了对顶角和邻补角,角平分线的定义,关键是掌握邻补角互补,对顶角相等.
29.30°##30度
【解析】根据邻补角性质,可得∠AOC+∠BOC=180°,结合已知∠AOC=5∠BOC,解方程可求∠BOC.
解:∵∠AOC与∠BOC互为邻补角,
∴∠AOC+∠BOC=180°,①
又∵∠AOC=5∠BOC,②
把②代入①,可得5∠BOC+∠BOC=180°,
解得∠BOC=30°.
故答案为:30°.
此题考查的是角的计算,能够根据邻补角的定义列出方程是解决此题关键.
30.36°
【解析】先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,根据角平分线定义得到∠AOC∠EOC72°=36°,然后根据对顶角相等得到∠BOD=∠AOC=36°.
解:设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∵OA平分∠EOC,
∴∠AOC∠EOC72°=36°,
∴∠BOD=∠AOC=36°.
故答案为:36°
考查了角的计算,角平分线的定义和对顶角的性质.解题的关键是明确:直角=90°;平角=180°,以及对顶角相等.
31.(1)∠DOE=120°;
(2)∠AOF=45°.
【解析】(1)根据角平分线的定义,得出∠EOC=∠BOE=60°,利用邻补角定义求出∠DOE即可;
(2)根据角平分线的定义,∠BOD:∠BOE=2:3,求出∠BOD,再根据对顶角可求出∠AOC,利用垂直,求出∠AOF.
(1)
解:∵OE平分∠BOC,∠BOE=60°,
∴∠EOC=∠BOE=60°,
∴∠DOE=180°-60°=120°;
(2)
解:∵∠BOD:∠BOE=2:3,
设∠BOD=x,则∠COE=∠BOE=x,
∵∠COE+∠BOE+∠BOD=180°,
∴x+x+x=180°,
∴x=45°,即∠BOD=45°,
∵OF⊥CD,∠AOC=∠BOD=45°,
∴∠COF=90°,
∴∠AOF=90°-45°=45°.
本题考查了角平分线定义,邻补角定义,对顶角性质,垂直定义,角的计算等;正确找出各个角之间的关系是正确计算的关键.
32.∠BOD=15°.
【解析】本题需先结合图形,得出∠AOC的度数,再根据OD平分∠AOC,得出∠AOD的度数,最后即可求出正确答案.
解:∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=150°.
∵OD平分∠AOC,
∴∠AOD=∠COD=∠AOC=75°,
∴∠BOD=∠AOB-∠AOD=15°.
本题主要考查了角平分线定义的应用以及角的计算.利用图形计算角的和差是解题的关键.
33.(1),
(2)160°
【解析】(1)根据对顶角和补角的定义,即可求解;
(2)根据,可得,从而得到,即可求解.
(1)
解:根据题意得:的对顶角为;
的补角是,
故答案为:,;
(2)
解:∵,,
∴,
∵,
∴,
∵,
∴.
本题主要考查了对顶角和补角的定义,角的和与差,邻补角的性质,熟练掌握对顶角和补角的定义,邻补角的性质是解题的关键.
34.∠3=50°,∠2=65°.
【解析】根据平角为180度可得∠3=180°-∠1-∠FOC ,根据对顶角相等可得∠AOD的度数,然后再根据角平分线定义进行计算即可
解:∵∠AOB=180°,
∴∠1+∠3+∠COF=180°,
∵∠FOC=90°,∠1=40°,
∴∠3=180°-∠1-∠FOC=50°, ∠BOC=∠1+∠FOC=130°,
∴∠AOD=∠BOC=130°,
∵OE平分∠AOD,
∴∠2=∠AOD=65°.
本题主要考查了对顶角,邻补角性质,角平分线的定义,掌握以上知识是解题的关键.
35.(1)70°,20°;(2)150°
【解析】(1)根据题意及余角、对顶角的意义可直接进行求解;
(2)设,则,则有,进而根据角的和差关系可求解.
解:(1),,
,;
(2)设,则,
,
即,
解得,,
,
.
本题主要考查余补角、对顶角的意义及一元一次方程的应用,熟练掌握余补角、对顶角的意义及一元一次方程的应用是解题的关键.
36.(1)∠BOE=154°;
(2)∠COE=42°.
【解析】(1)根据对顶角的定义,由∠AOC与∠BOD是对顶角,得∠AOC=∠BOD=65°.由∠AOE:∠EOC=2:3,求得∠AOE=∠AOC=26°.根据邻补角的定义,得∠BOE=180°-∠AOE=154°.
(2)设∠AOE=2x,∠EOC=3x.由∠AOE=∠BOF-10°,得∠BOF=4x+20°.根据角平分线的定义,由OF平分∠BOE,得∠BOE=2∠BOF=8x+40°.根据邻补角的定义,得∠AOE+∠BOE=2x+8x+40°=180°,进而解决此题.
(1)
解:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=65°.
∵∠AOE:∠EOC=2:3,
∴∠AOE=∠AOC=26°.
∴∠BOE=180°-∠AOE=180°-26°=154°;
(2)
解:设∠AOE=2x,∠EOC=3x.
∵∠AOE=∠BOF-10°,
∴∠BOF=4x+20°.
∵OF平分∠BOE,
∴∠BOE=2∠BOF=8x+40°.
∴∠AOE+∠BOE=2x+8x+40°=180°.
∴x=14°.
∴∠COE=3x=42°.
本题主要考查了对顶角、邻补角、角平分线,熟练掌握对顶角、邻补角、角平分线的定义是解决本题的关键.
37.100°
【解析】根据对顶角相等以及角平分线的性质可得出∠AOE的度数,再根据平角的定义即可得出∠EOD的度数.
解:∵∠BOD=40°,
∴∠AOC=∠BOD=40°.
∵OA平分∠EOC,
∴∠AOE=∠AOC=40°,
∴.
本题主要考查了角平分线的性质以及对顶角、邻补角的性质,难度不大.
38.50°,25°.
【解析】根据邻补角的性质,可得∠AOD+∠BOD=180°,即,代入可得∠BOD,根据对顶角的性质,可得∠∠AOC的度数,根据角平分线的性质,可得∠DOE的数.
解:由邻补角的性质,得∠AOD+∠BOD=180°,即
∵,
∴.
∴,
∴∠AOC=∠BOD=50°,
∵OE平分∠BOD,得
∠DOE=∠DOB=25°.
本题考查了角平分线的定义,对顶角、邻补角的性质,解题关键是熟记相关性质,根据角之间的关系建立方程求解.
39.∠3=50°,∠2=65°.
【解析】根据邻补角的性质、角平分线的定义进行解答即可.
∵∠FOC=90°,∠1=40°,
∴∠3=180°-∠FOC-∠1 =180°-90°-40°=50°,
∴∠AOD=180°-∠3=180°-50°=130°,
又∵OE平分∠AOD,
∴∠2=∠AOD=65°.
本题考查的是邻补角的概念和性质、角平分线的定义,掌握邻补角之和等于180°是解题的关键.
40.(1)∠AOC、∠BOD;∠EOD、∠BOF;(2)∠EOF=144°.
【解析】(1)根据互余及互补的定义,结合图形进行判断即可;
(2)设∠AOC=x,则∠BOD=x,∠EOF=4x,根据周角为360度,即可解出x.
解:(1)图中与∠AOF互余的角是:∠AOC、∠BOD;
图中与∠COE互补的角是:∠EOD、∠BOF.
(2)∵OE⊥AB,OF⊥CD,
∴∠EOB=90°,∠FOD=90°,
又∵∠AOC=∠EOF,
设∠AOC=x,则∠BOD=x,∠EOF=4x,
根据题意可得:4x+x+90+90=360°,
解得:x=36°.
∴∠EOF=4x=144°.
本题考查了余角和补角的知识,注意结合图形进行求解.
41.(1)见解析
(2)
(3)
【解析】(1)根据定义直接求解即可;
(2)根据等角的补角相等可得,进而根据邻补角的定义求得,根据对顶角相等可得,进而根据角的和求解即可;
(3)根据角平分线的意义,以及角度的和差计算可得,即可求得答案.
(1)证明:OC平分∠BOD射线OB为∠BOC与∠AOC的“互补线”
(2)射线OE为∠BOC与∠BOE的“互补线”,
(3)射线OB为∠BOC与∠AOC的“互补线”,射线OE、OF分别平分∠AOC、∠BOC,
本题考查了新定义,等角的补角相等,根据邻补角求角度,角平分线的意义,几何图形中角度的和差关系,理解题意,数形结合是解题的关键.
42.(1)2
(2)
(3)或
【解析】(1)由邻补角和余角的定义求出两个角,即可得出结论;
(2)由角平分线的定义可得,再根据,从而可求解;
(3)分两种情况讨论:①是内;②在外,分析清楚角关系求解即可.
(1)
解:,与射线重合,
,
,
,
,
故答案为:2;
(2)
解:由(1)得,,
是的角平分线,
,
,
;
(3)
解:能,
①当是内时,有:
,,
则,
解得:;
②当在外时,有:
,,
则,
解得:.
综上所述,的度数为或.
本题主要考查三角形的内角和定理,余角和补角,解题的关键是结合图形分析清楚角与角之间的关系.
43.(1),理由见解析;(2)
【解析】(1)利用垂直的定义以及同角的余角相等可得出∠COE=∠BOF;
(2)通过垂直的定义得到∠COA=90°,再由已知∠2-∠1=20°,得到∠1、∠2的值,然后由角平分线的定义得出结果.
解:(1)∵CO⊥AB,OF⊥OE,
∴∠COE+∠BOE=∠BOE+∠BOF=90°
∴∠COE=∠BOF;
(2)∵CO⊥AB,
∴∠COA=90°,即∠2=90°-∠1,
又∵∠2-∠1=20°,
∴∠2=20°+∠1,
∴90°-∠1=20°+∠1,
解得:∠1=35°,
∴∠2=55°,
∴∠BOD=180°-∠2=125°,
∵OE是∠BOD的平分线,
∴∠BOE=∠DOE=∠BOD=62.5°.
本题考查垂直和角平分线的定义,同角的余角相等,掌 握相关概念正确推理计算是解题关键.
44.(1)∠BOC=∠BOE.
(2)①存在,t=2.5或10或31;②40°
【解析】(1)由∠AOB=90°知∠BOC+∠AOC=90°、∠AOD+∠BOE=90°,根据∠AOD=∠AOC可得答案;
(2)①当OA平分∠COD时∠AOD=∠AOC、当OC平分∠AOD时∠AOC=∠COD、当OD平分∠AOC时∠AOD=∠COD,分别列出关于t的方程,解之可得;
②根据角的和差即可得到结论.
(1)
解:∠BOC=∠BOE.
理由如下:
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,∠AOD+∠BOE=90°,
∵OA平分∠COD,
∴∠AOD=∠AOC,
∴∠BOC=∠BOE,
故答案为:∠BOC=∠BOE;
(2)
①存在.
理由:∵∠COE=130°,
∴∠COD=180°﹣130°=50°,
当OA平分∠COD时,∠AOD=∠AOC=∠COD,即10t=25,解得t=2.5;
当OC平分∠AOD时,∠AOC=∠COD,即10t﹣50=50,解得t=10;
当OD平分∠AOC时,∠AOD=∠COD,即360﹣10t=50,解得:t=31;
综上所述,t的值为2.5、10、31;
②∵∠AOC=∠COE﹣∠AOE=130°﹣∠AOE,∠BOE=90°﹣∠AOE,
∴∠AOC﹣∠BOE=(130°﹣∠AOE)﹣(90°﹣∠AOE)=40°,
∴∠AOC﹣∠BOE的值为40°.
本题主要考查角平分线的定义、余角的性质及角的计算,根据题意全面考虑所有可能以分类讨论是解题的关键.
45.(1)50
(2)25秒
(3)11或47
【解析】(1)由余角的性质可求解;
(2)由角的数量关系列出等式可求解;
(3)分两种情况讨论即可.
(1)
解:∵∠DOE=90°,∠BOC=40°,
∴∠COE=∠DOE-∠BOC=90°-40°=50°,
故答案为:50;
(2)
解:∵三角板DOE绕点O以每秒2°的速度按逆时针方向旋转,
∴经过t秒,∠COD=∠BOD-∠BOC=2t-40 ,∠AOE=90 -2t,
∵,
∴2t-40 =(90 -2t),
解得t=25.
即运动时间为25秒.
(3)
解:图2中∠AOE=90 -2t=40 ,∠D1O E1=∠DOE=90
∵三角板DOE再绕点O以每秒5°的速度按顺时针转方向旋转一周,
情况①如图:
经过秒后,∠EOE1=5t
∵直线OC恰好平分,
∴
∵∠BOC=40
∠AOC=∠AOE+∠EOE1+=140
即40 +5t+45 =140
解得:t=11;
情况②如图:
此时有:5t-10 -45 =180 ,
解得t=47
故的值为11或47.
本题考查了一元一次方程的应用,角平分线的定义,平角的性质等知识,熟练运用这些性质解决问题是本题的关键.
46.(1),
(2)或
(3)答案见解析
【解析】(1)根据补角的定义可求度数,在利用角平分线的定义可求解度数,进而求解的度数;
(2)分两种情况:当在的外部时,当在的内部时,利用补角的定义结合角平分线的定义可求解;
(3)可分两种情况:当和互为邻补角时,即和在的不同侧时;当和在的同一侧时。而对于当和在的同一侧时可分为:当 时;当时;当时分别计算求解即可.
(1)
解:与互为补角,
,
,
平分,
,
,
故答案为:,;
(2)
解:当在的外部时,
与互为补角,
,
平分,
,
,
当在的内部时,
与互为补角,
,
平分,
,
,
的度数为或;
(3)
当和互为邻补角时,即和在的不同侧时,
,
,
平分,
,
,
即此时;
当和在的同一侧时,
当,如图,此时,,
平分,
,和重合,
;
当时,如图,
,,
平分,
,
,
,
即,此时,
当,如图,,,
平分,
,
,
即,此时,
综上,当和在的不同侧时,
,此时;
当和在的同一侧时,
当时,;
当时,;
当时,.
本题主要考查角的计算,三角形的外角定义,角平分线的性质,分类讨论是解决问题的关键.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
