2021-2022学年江苏省各地苏科版数学八年级上册 2.2-2.3轴对称的性质、设计轴对称图案 同步练习(Word版,含解析)
文档属性
| 名称 | 2021-2022学年江苏省各地苏科版数学八年级上册 2.2-2.3轴对称的性质、设计轴对称图案 同步练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 688.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 09:34:19 | ||
图片预览



文档简介
2.2-2.3 轴对称的性质、设计轴对称图案
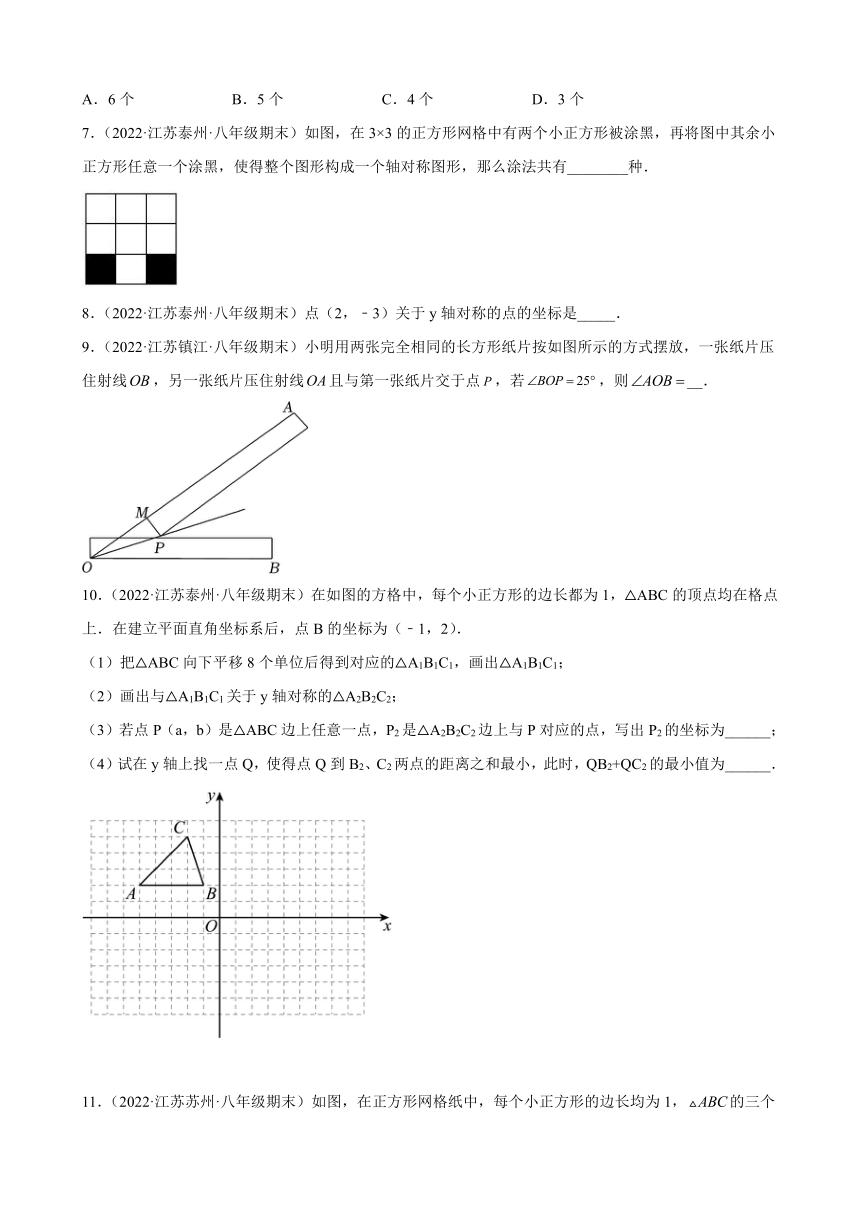
1.(2022·江苏宿迁·八年级期末)直角坐标系中的点A(2,-3)关于x轴对称的点B的坐标( )
A.(2,3 ) B.(2,-3) C.(-2,3) D.(-2,-3)
2.(2022·江苏泰州·八年级期末)点P(1,﹣2)关于x轴对称的点的坐标为( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
3.(2022·江苏南京·八年级期末)在平面直角坐标系中,点关于y轴对称的点的坐标是( )
A. B. C. D.
4.(2022·江苏无锡·八年级期末)下列图形中,是轴对称图形且对称轴条数最多的是( )
A. B. C. D.
5.(2022·江苏·南京玄武外国语学校八年级期末)如图,点在锐角的内部,连接,,点关于、所在直线的对称点分别是、,则、两点之间的距离可能是( )
A.8 B.7 C.6 D.5
6.(2022·江苏南通·八年级期末)如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中与成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
7.(2022·江苏泰州·八年级期末)如图,在3×3的正方形网格中有两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形构成一个轴对称图形,那么涂法共有________种.
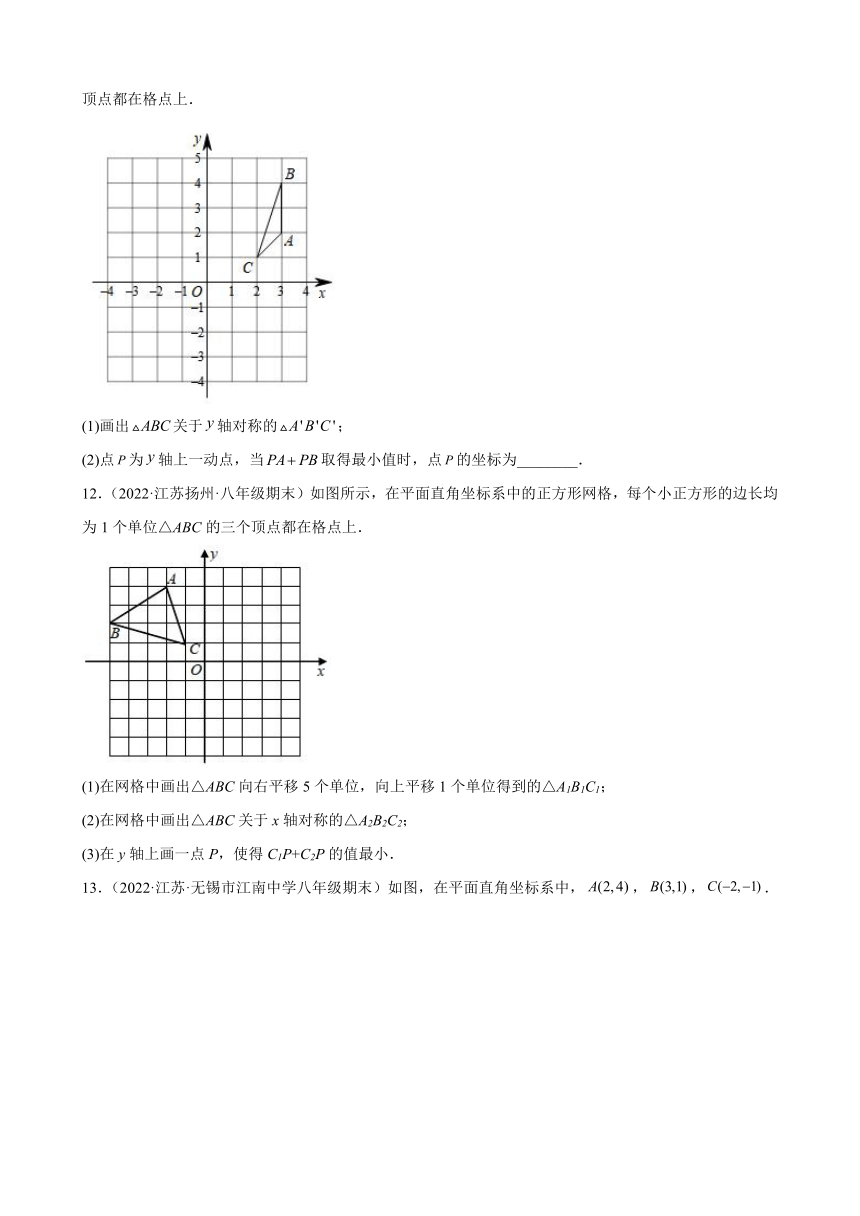
8.(2022·江苏泰州·八年级期末)点(2,﹣3)关于y轴对称的点的坐标是_____.
9.(2022·江苏镇江·八年级期末)小明用两张完全相同的长方形纸片按如图所示的方式摆放,一张纸片压住射线,另一张纸片压住射线且与第一张纸片交于点,若,则__.
10.(2022·江苏泰州·八年级期末)在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为______;
(4)试在y轴上找一点Q,使得点Q到B2、C2两点的距离之和最小,此时,QB2+QC2的最小值为______.
11.(2022·江苏苏州·八年级期末)如图,在正方形网格纸中,每个小正方形的边长均为1,的三个顶点都在格点上.
(1)画出关于轴对称的;
(2)点为轴上一动点,当取得最小值时,点的坐标为________.
12.(2022·江苏扬州·八年级期末)如图所示,在平面直角坐标系中的正方形网格,每个小正方形的边长均为1个单位△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向右平移5个单位,向上平移1个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于x轴对称的△A2B2C2;
(3)在y轴上画一点P,使得C1P+C2P的值最小.
13.(2022·江苏·无锡市江南中学八年级期末)如图,在平面直角坐标系中,,,.
(1)在图中作出关于x轴的对称图形;
(2)点,,的坐标分别是______,______,______;
(3)的面积为______.
参考答案:
1.A
【解析】根据对称的性质知,直角坐标系中的点A(2,-3)关于x轴对称,则x不变,y变相反数,即可求出B点坐标.
根据对称的性质知,直角坐标系中的点A(2,-3)关于x轴对称,则x不变,y变相反数,则B的坐标为(2,3),故选A.
本题是对坐标系中对称点的考查,熟知点关于x轴对称,则x不变,y变相反数;关于y轴对称,则y不变,x变相反数是解决本题的关键.
2.A
【解析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
点P(1,-2)关于x轴的对称点的坐标是(1,2),
故选A.
此题考查平面直角坐标系点的对称性质,解决本题的关键是熟记得出的性质.
3.B
【解析】在平面直角坐标系中,点关于y轴对称的点的坐标特征是横坐标变为相反数,纵坐标不变,据此解题.
在平面直角坐标系中,点关于y轴对称的点的坐标是,
故选:B.
本题考查象限与点坐标特征等知识,是重要考点,难度较易,掌握相关知识是解题关键.
4.D
【解析】利用轴对称图形的定义逐一判断即可.
解:A是轴对称图形,对称轴有1条;
B不是轴对称图形;
C不是轴对称图形;
D是轴对称图形,对称轴有2条;
故选:D.
本题考查识别轴对称图形,掌握轴对称图形的定义是解题的关键.
5.D
【解析】由对称得OP1=OP=3,OP=OP2=3,再根据三角形任意两边之和大于第三边,即可得出结果.
解:连接OP1,OP2,P1P2,
∵点P关于直线l,m的对称点分别是点P1,P2,
∴OP1=OP=3,OP=OP2=3, OP1+OP2>P1P2, 0<P1P2<6,
所以A,B,C不符合题意,D符合题意;
故选D
本题考查了轴对称的性质,三角形三边之间的关系,解本题的关键熟练掌握对称性和三角形三边的关系.
6.A
【解析】直接利用轴对称图形的性质分别得出符合题意的答案.
解:符合题意的三角形如图所示:分三类
对称轴为横向:
对称轴为纵向:
对称轴为斜向:
满足要求的图形有6个.
故选:A.
本题主要考查利用轴对称来设计轴对称图形,关键是要掌握轴对称的性质和轴对称图形的含义.
7.5
【解析】根据轴对称图形的定义,即可求解.
解:如图所示:所标数字之处都可以构成轴对称图形,共有5种情形,
故答案为:5.
本题主要考查了轴对称图形的定义,熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合,这样的图形就叫做轴对称图形,这条直线叫做对称轴是解题的关键.
8.(﹣2,﹣3)
【解析】直接利用关于y轴对称点的性质得出答案.
点(2,﹣3)关于y轴对称的点的坐标是:(﹣2,﹣3).
故答案为:(﹣2,﹣3).
本题主要考查了关于y轴对称点的性质,平面直角坐标系中任意一点P(x,y),关于y轴的对称点的坐标是(-x,y),即关于纵轴的对称点,纵坐标不变,横坐标变成相反数.正确记忆横纵坐标的关系是解题关键.
9.
【解析】过点作于点,于点,然后由长方形纸片完全相同得到,再用定理证明,进而得到,进而可得到的大小.
解:如图,过点作于点,于点,则,
两张长方形纸片完全相同,
,
在和中,
∵,
∴,
,
,
,
,
故答案为:.
本题考查了三角形全等的判定与性质,折叠的性质.解题的关键在于证明三角形全等.
10.(1)作图见解析;(2)作图见解析;(3)(-a,b-8);(4)3.
【解析】(1)分别将点A、B、C向下平移8个单位,然后顺次连接;
(2)分别作出点A1、B1、C1关于y轴对称的点,然后顺次连接;
(3)根据所作图形写出P2的坐标;
(4)作出点B2关于y轴的对称点B1,连接B1C2,与y轴的交点即为点Q,然后求出最小值.
(1)所作图形如图所示:
(2)所作图形如图所示:
(3)P2的坐标为(﹣a,b﹣8);
(4)点Q如图所示:QB2+QC2==3.
11.(1)见解析
(2)(0,3)
【解析】(1)利用关于y轴对称的点的坐标得到A′、B′、C′的坐标,然后描点即可;
(2)连接BA′交y轴于P点,根据两点之间线段最短可判断P点满足条件,从而得到P点坐标.
(1)
解:如图,△A'B'C'为所作;
(2)
如图,根据轴对称的性质可知,,连接BA′交y轴于P点,此时点P为所求作,P点坐标为(0,3).
故答案为:(0,3).
本题考查了作图-轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了最短路径问题.
12.(1)见解析
(2)见解析
(3)见解析
【解析】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出A,B,C的对应点A2,B2,C2即可.
(3)连接C1C2交y轴于点P,点P即为所求作.
(1)
解:如图,△A1B1C1即为所求作.
(2)
解:如图,△A2B2C2即为所求作.
(3)
解:如图,点P即为所求作.
本题考查作图﹣轴对称变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
13.(1)见解析;(2);;;(3).
【解析】(1)首先作出A、B、C三点关于x轴的对称点,再顺次连接即可;
(2)根据(1)得出对应点位置进而得出答案;
(3)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
解:(1)如图所示,
(2)点,,的坐标分别是;;;
故答案为:;;;
(3)S△ABC=5×5-×4×5-×1×3-×2×5=;
故答案为:.
此题主要考查了轴对称变换以及三角形面积求法,正确得出对应点位置是解题关键.
1.(2022·江苏宿迁·八年级期末)直角坐标系中的点A(2,-3)关于x轴对称的点B的坐标( )
A.(2,3 ) B.(2,-3) C.(-2,3) D.(-2,-3)
2.(2022·江苏泰州·八年级期末)点P(1,﹣2)关于x轴对称的点的坐标为( )
A.(1,2) B.(1,﹣2) C.(﹣1,2) D.(﹣1,﹣2)
3.(2022·江苏南京·八年级期末)在平面直角坐标系中,点关于y轴对称的点的坐标是( )
A. B. C. D.
4.(2022·江苏无锡·八年级期末)下列图形中,是轴对称图形且对称轴条数最多的是( )
A. B. C. D.
5.(2022·江苏·南京玄武外国语学校八年级期末)如图,点在锐角的内部,连接,,点关于、所在直线的对称点分别是、,则、两点之间的距离可能是( )
A.8 B.7 C.6 D.5
6.(2022·江苏南通·八年级期末)如图,在的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的为格点三角形,在图中与成轴对称的格点三角形可以画出( )
A.6个 B.5个 C.4个 D.3个
7.(2022·江苏泰州·八年级期末)如图,在3×3的正方形网格中有两个小正方形被涂黑,再将图中其余小正方形任意一个涂黑,使得整个图形构成一个轴对称图形,那么涂法共有________种.
8.(2022·江苏泰州·八年级期末)点(2,﹣3)关于y轴对称的点的坐标是_____.
9.(2022·江苏镇江·八年级期末)小明用两张完全相同的长方形纸片按如图所示的方式摆放,一张纸片压住射线,另一张纸片压住射线且与第一张纸片交于点,若,则__.
10.(2022·江苏泰州·八年级期末)在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为______;
(4)试在y轴上找一点Q,使得点Q到B2、C2两点的距离之和最小,此时,QB2+QC2的最小值为______.
11.(2022·江苏苏州·八年级期末)如图,在正方形网格纸中,每个小正方形的边长均为1,的三个顶点都在格点上.
(1)画出关于轴对称的;
(2)点为轴上一动点,当取得最小值时,点的坐标为________.
12.(2022·江苏扬州·八年级期末)如图所示,在平面直角坐标系中的正方形网格,每个小正方形的边长均为1个单位△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向右平移5个单位,向上平移1个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于x轴对称的△A2B2C2;
(3)在y轴上画一点P,使得C1P+C2P的值最小.
13.(2022·江苏·无锡市江南中学八年级期末)如图,在平面直角坐标系中,,,.
(1)在图中作出关于x轴的对称图形;
(2)点,,的坐标分别是______,______,______;
(3)的面积为______.
参考答案:
1.A
【解析】根据对称的性质知,直角坐标系中的点A(2,-3)关于x轴对称,则x不变,y变相反数,即可求出B点坐标.
根据对称的性质知,直角坐标系中的点A(2,-3)关于x轴对称,则x不变,y变相反数,则B的坐标为(2,3),故选A.
本题是对坐标系中对称点的考查,熟知点关于x轴对称,则x不变,y变相反数;关于y轴对称,则y不变,x变相反数是解决本题的关键.
2.A
【解析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
点P(1,-2)关于x轴的对称点的坐标是(1,2),
故选A.
此题考查平面直角坐标系点的对称性质,解决本题的关键是熟记得出的性质.
3.B
【解析】在平面直角坐标系中,点关于y轴对称的点的坐标特征是横坐标变为相反数,纵坐标不变,据此解题.
在平面直角坐标系中,点关于y轴对称的点的坐标是,
故选:B.
本题考查象限与点坐标特征等知识,是重要考点,难度较易,掌握相关知识是解题关键.
4.D
【解析】利用轴对称图形的定义逐一判断即可.
解:A是轴对称图形,对称轴有1条;
B不是轴对称图形;
C不是轴对称图形;
D是轴对称图形,对称轴有2条;
故选:D.
本题考查识别轴对称图形,掌握轴对称图形的定义是解题的关键.
5.D
【解析】由对称得OP1=OP=3,OP=OP2=3,再根据三角形任意两边之和大于第三边,即可得出结果.
解:连接OP1,OP2,P1P2,
∵点P关于直线l,m的对称点分别是点P1,P2,
∴OP1=OP=3,OP=OP2=3, OP1+OP2>P1P2, 0<P1P2<6,
所以A,B,C不符合题意,D符合题意;
故选D
本题考查了轴对称的性质,三角形三边之间的关系,解本题的关键熟练掌握对称性和三角形三边的关系.
6.A
【解析】直接利用轴对称图形的性质分别得出符合题意的答案.
解:符合题意的三角形如图所示:分三类
对称轴为横向:
对称轴为纵向:
对称轴为斜向:
满足要求的图形有6个.
故选:A.
本题主要考查利用轴对称来设计轴对称图形,关键是要掌握轴对称的性质和轴对称图形的含义.
7.5
【解析】根据轴对称图形的定义,即可求解.
解:如图所示:所标数字之处都可以构成轴对称图形,共有5种情形,
故答案为:5.
本题主要考查了轴对称图形的定义,熟练掌握若一个图形沿着一条直线折叠后两部分能完全重合,这样的图形就叫做轴对称图形,这条直线叫做对称轴是解题的关键.
8.(﹣2,﹣3)
【解析】直接利用关于y轴对称点的性质得出答案.
点(2,﹣3)关于y轴对称的点的坐标是:(﹣2,﹣3).
故答案为:(﹣2,﹣3).
本题主要考查了关于y轴对称点的性质,平面直角坐标系中任意一点P(x,y),关于y轴的对称点的坐标是(-x,y),即关于纵轴的对称点,纵坐标不变,横坐标变成相反数.正确记忆横纵坐标的关系是解题关键.
9.
【解析】过点作于点,于点,然后由长方形纸片完全相同得到,再用定理证明,进而得到,进而可得到的大小.
解:如图,过点作于点,于点,则,
两张长方形纸片完全相同,
,
在和中,
∵,
∴,
,
,
,
,
故答案为:.
本题考查了三角形全等的判定与性质,折叠的性质.解题的关键在于证明三角形全等.
10.(1)作图见解析;(2)作图见解析;(3)(-a,b-8);(4)3.
【解析】(1)分别将点A、B、C向下平移8个单位,然后顺次连接;
(2)分别作出点A1、B1、C1关于y轴对称的点,然后顺次连接;
(3)根据所作图形写出P2的坐标;
(4)作出点B2关于y轴的对称点B1,连接B1C2,与y轴的交点即为点Q,然后求出最小值.
(1)所作图形如图所示:
(2)所作图形如图所示:
(3)P2的坐标为(﹣a,b﹣8);
(4)点Q如图所示:QB2+QC2==3.
11.(1)见解析
(2)(0,3)
【解析】(1)利用关于y轴对称的点的坐标得到A′、B′、C′的坐标,然后描点即可;
(2)连接BA′交y轴于P点,根据两点之间线段最短可判断P点满足条件,从而得到P点坐标.
(1)
解:如图,△A'B'C'为所作;
(2)
如图,根据轴对称的性质可知,,连接BA′交y轴于P点,此时点P为所求作,P点坐标为(0,3).
故答案为:(0,3).
本题考查了作图-轴对称变换:几何图形都可看作是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的.也考查了最短路径问题.
12.(1)见解析
(2)见解析
(3)见解析
【解析】(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)分别作出A,B,C的对应点A2,B2,C2即可.
(3)连接C1C2交y轴于点P,点P即为所求作.
(1)
解:如图,△A1B1C1即为所求作.
(2)
解:如图,△A2B2C2即为所求作.
(3)
解:如图,点P即为所求作.
本题考查作图﹣轴对称变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
13.(1)见解析;(2);;;(3).
【解析】(1)首先作出A、B、C三点关于x轴的对称点,再顺次连接即可;
(2)根据(1)得出对应点位置进而得出答案;
(3)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案.
解:(1)如图所示,
(2)点,,的坐标分别是;;;
故答案为:;;;
(3)S△ABC=5×5-×4×5-×1×3-×2×5=;
故答案为:.
此题主要考查了轴对称变换以及三角形面积求法,正确得出对应点位置是解题关键.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
