2022—2023学年人教版数学八年级上册11.2.1三角形的内角 导学案 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.1三角形的内角 导学案 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 376.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 17:08:28 | ||
图片预览

文档简介
11.2.1三角形的内角
【学习目标】
1.经历实验活动的过程,知道三角形的内角和定理,会用平行线的性质推出这一定理。
2.会应用三角形内角和定理解决一些简单的实际问题。
【学习重难点】
1.探索并证明三角形内角和定理,体会证明的必要性。
2.如何添加辅助线证明三角形内角和定理。
【学习过程】
一、发现并证明“三角形的内角和等于180°”。
(1)在纸上画一个三角形,并将它的内角剪下拼合在一起,就得到一个平角。在小组内展示拼合的方法。
(2)从上面的操作过程中,你能找到证明“三角形三个内角的和等于180°”的思路吗?在小组内说说你的思路。
(3)请你自选一种作辅助线的方法,证明“三角形三个内角的和等于180°”。
已知:△ABC(如图)。
求证:∠A+∠B+∠C=180°。
证明:
三角形内角和定理:三角形三个内角的和等于180°。
二、证明“直角三角形的两个锐角互余”。
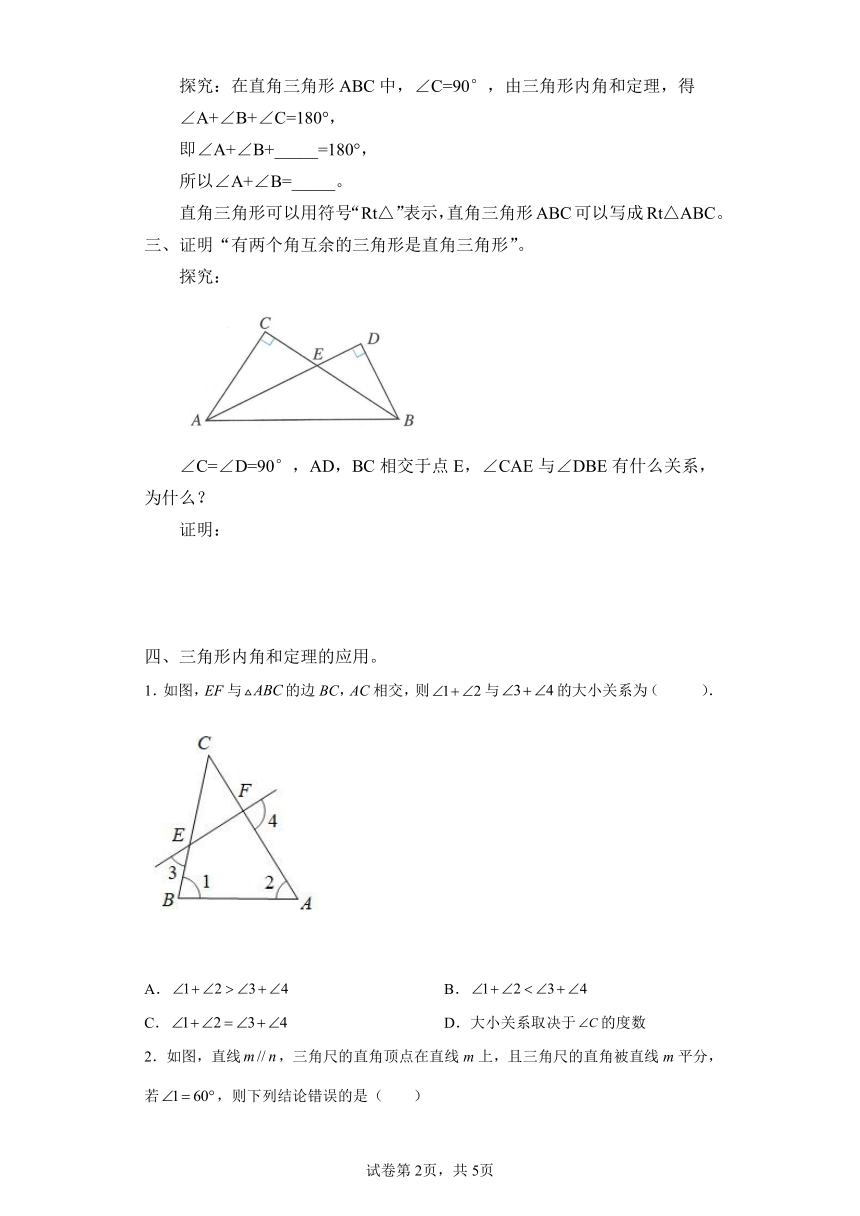
探究:在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C=180°,
即∠A+∠B+_____=180°,
所以∠A+∠B=_____。
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC。
三、证明“有两个角互余的三角形是直角三角形”。
探究:
∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系,为什么?
证明:
四、三角形内角和定理的应用。
1.如图,EF与的边BC,AC相交,则与的大小关系为( ).
A. B.
C. D.大小关系取决于的度数
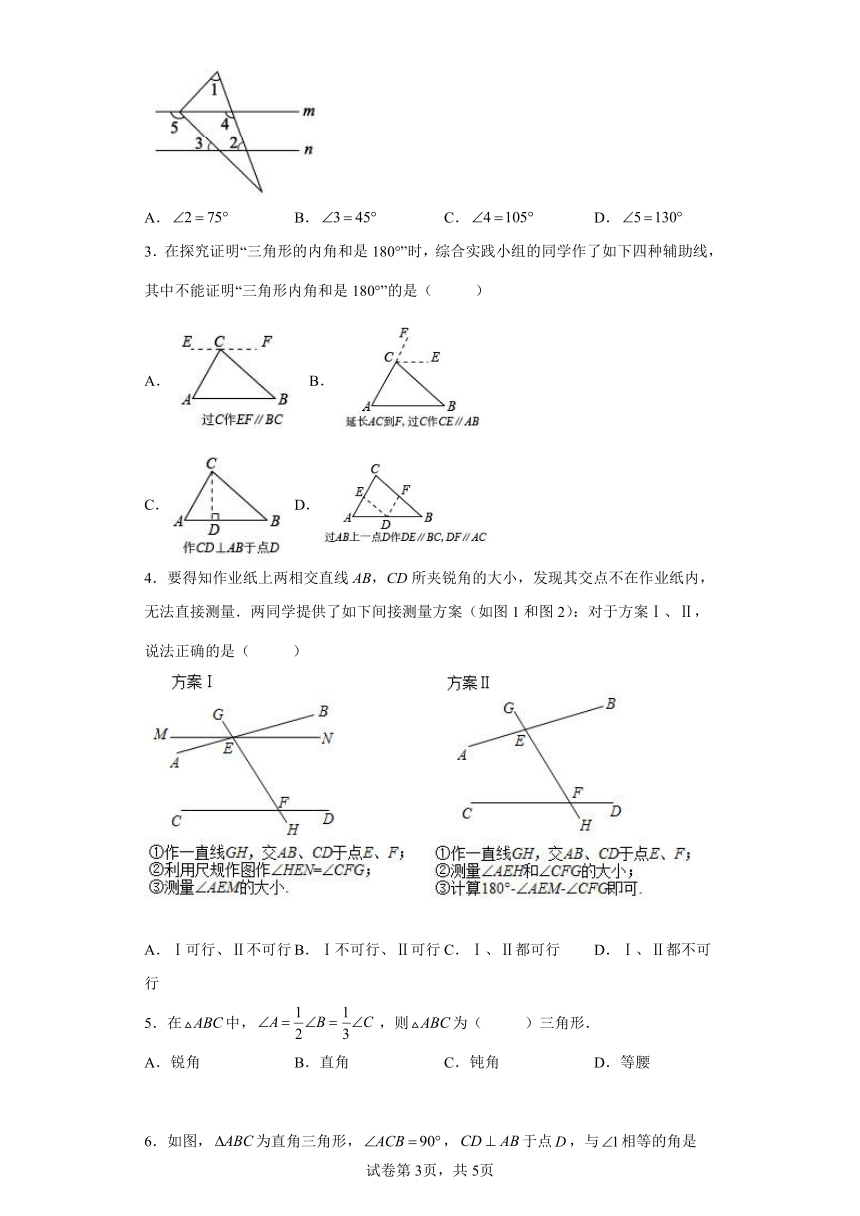
2.如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
3.在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )
A.B.
C. D.
4.要得知作业纸上两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案Ⅰ、Ⅱ,说法正确的是( )
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行 C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
5.在中,,则为( )三角形.
A.锐角 B.直角 C.钝角 D.等腰
6.如图,为直角三角形,,于点,与相等的角是__________.
7.如图所示,在中,,点D在边上,.若,则_____度.
8.如图,在中,,,是线段上一个动点,连接,把沿折叠,点落在同一平面内的点处,当平行于的边时,的大小为______.
9.如图,在中,,,是的高,平分交于,求的度数.
10.如图,,于D,于G,.
(1)求∠2的度数;
(2)若CD平分∠ACB,求的度数.
11.如图,D、E、F、G是△ABC边上的点,,.
若BE平分,,,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.D
3.C
4.C
5.B
6.∠B
7.58
8.67°或118°
9..
10.(1)40°
(2)50°
11.
4 / 4
【学习目标】
1.经历实验活动的过程,知道三角形的内角和定理,会用平行线的性质推出这一定理。
2.会应用三角形内角和定理解决一些简单的实际问题。
【学习重难点】
1.探索并证明三角形内角和定理,体会证明的必要性。
2.如何添加辅助线证明三角形内角和定理。
【学习过程】
一、发现并证明“三角形的内角和等于180°”。
(1)在纸上画一个三角形,并将它的内角剪下拼合在一起,就得到一个平角。在小组内展示拼合的方法。
(2)从上面的操作过程中,你能找到证明“三角形三个内角的和等于180°”的思路吗?在小组内说说你的思路。
(3)请你自选一种作辅助线的方法,证明“三角形三个内角的和等于180°”。
已知:△ABC(如图)。
求证:∠A+∠B+∠C=180°。
证明:
三角形内角和定理:三角形三个内角的和等于180°。
二、证明“直角三角形的两个锐角互余”。
探究:在直角三角形ABC中,∠C=90°,由三角形内角和定理,得
∠A+∠B+∠C=180°,
即∠A+∠B+_____=180°,
所以∠A+∠B=_____。
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt△ABC。
三、证明“有两个角互余的三角形是直角三角形”。
探究:
∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系,为什么?
证明:
四、三角形内角和定理的应用。
1.如图,EF与的边BC,AC相交,则与的大小关系为( ).
A. B.
C. D.大小关系取决于的度数
2.如图,直线,三角尺的直角顶点在直线m上,且三角尺的直角被直线m平分,若,则下列结论错误的是( )
A. B. C. D.
3.在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )
A.B.
C. D.
4.要得知作业纸上两相交直线AB,CD所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案(如图1和图2):对于方案Ⅰ、Ⅱ,说法正确的是( )
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行 C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
5.在中,,则为( )三角形.
A.锐角 B.直角 C.钝角 D.等腰
6.如图,为直角三角形,,于点,与相等的角是__________.
7.如图所示,在中,,点D在边上,.若,则_____度.
8.如图,在中,,,是线段上一个动点,连接,把沿折叠,点落在同一平面内的点处,当平行于的边时,的大小为______.
9.如图,在中,,,是的高,平分交于,求的度数.
10.如图,,于D,于G,.
(1)求∠2的度数;
(2)若CD平分∠ACB,求的度数.
11.如图,D、E、F、G是△ABC边上的点,,.
若BE平分,,,求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.D
3.C
4.C
5.B
6.∠B
7.58
8.67°或118°
9..
10.(1)40°
(2)50°
11.
4 / 4
