人教版数学八年级上册 15.3 分式方程 课时练 (Word版,含答案)
文档属性
| 名称 | 人教版数学八年级上册 15.3 分式方程 课时练 (Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览




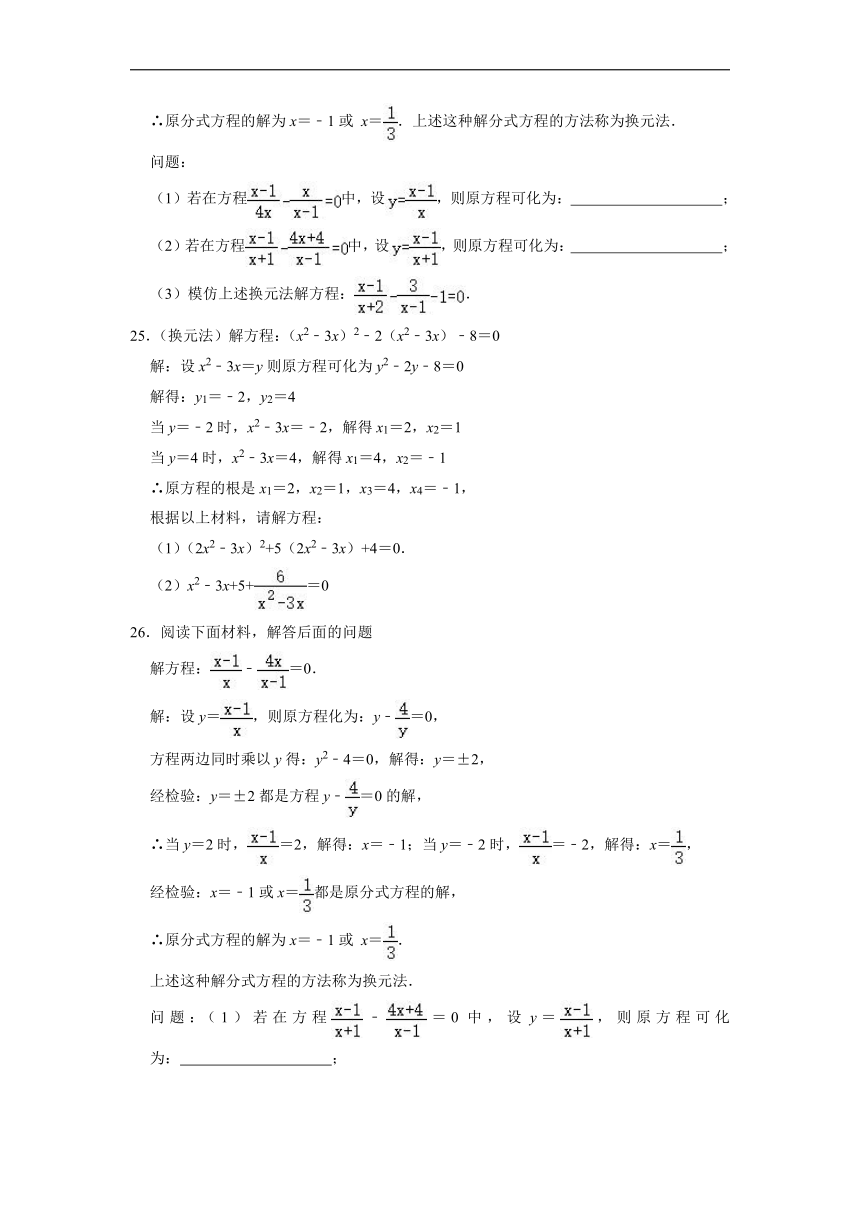
文档简介
《15.3分式方程》课时练
1.下列方程:①;②=2;③y=x;④=;⑤y+1=;⑥1+3(x﹣2)=7﹣x;⑦y2﹣3=.其中,分式方程有( )个.
A.1 B.2 C.3 D.4
2.若关于x的分式方程=2的解为非负数,则m的取值范围是( )
A.m>﹣1 B.m≥1 C.m>﹣1且m≠1 D.m≥﹣1且m≠1
3.甲乙两地相距300km,新修的高速公路开通后,在甲乙两地间行驶的长途客运车的平均速度提高了40%,而从甲乙两地的时间缩短了1.6h,试确定原来的车速.设原来的车速为xkm/h,下列列出的方程正确的是( )
A.=1.6 B.=1.6
C.=1.6 D.=1.6
4.几名同学包租一辆面包车去大山铺恐龙博物馆参观,面包车的租价为180元,出发时又增加了两名同学,结果每名同学比原来少摊了3元钱车费.设原来参加游览的同学供x名,则所列方程为( )
A. B.
C. D.
5.A地在河的上游,B地在河的下游,若船从A地开往B地的速度为V1,从B地返回A地的速度为V2,则A,B两地间往返一次的平均速度为( )
A. B.
C. D.无法计算
6.甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )
A.= B.=
C.= D.=
7.已知实数x满足x2++x﹣=4,则x﹣的值是( )
A.﹣2 B.1 C.﹣1或2 D.﹣2或1
8.分式方程=有增根,则m的值为( )
A.0和3 B.1 C.1和﹣2 D.3
9.下列方程是关于x的方程,其中是分式方程的是 (只填序号)
①=5;②+2=;③;④;⑤1+=2﹣;⑥;⑦;⑧;⑨.
10.关于x的分式方程的解为正数,则m的取值范围是 .
11.若关于x的方程=+1无解,则a的值是 .
12.若关于x的分式方程﹣1=无解,则m的值 .
13.若x为实数,且+x2+2x=﹣2,则x2+2x的值为 .
14.某市为治理污水,需要铺设一段全长600m的污水排放管道,铺设120m后,为加快施工进度,后来每天比原计划增加20m,结果共用11天完成这一任务,求原计划每天铺设管道的长度.如果设原计划每天铺设xm管道,那么根据题意,可列方程 .
15.观察下列方程的特征及其解的特点;
①x+=﹣3的解为x1=﹣1,x2=﹣2.
②x+=﹣5的解为x1=﹣2,x2=﹣3.
③x+=﹣7的解为x1=﹣3,x2=﹣4;
解答下列问题;
(1)请你写出一个符合上述特征的方程为 ,其解为 .
(2)根据这类方程特征,写出第n个方程为 ,其解为 .
(3)请利用(2)的结论,求关于x的方程x+=﹣2(n+2)(其中n为正整数)的解.
16.解分式方程.
(1) (2).
17.解方程:.
18.昆明市某学校2018年在商场购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球的数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球,一个乙种足球各需多少元?
(2)为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对甲种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,如果此次购买甲、乙两种足球的费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
19.京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
20.为了保护水资源,实行节约用水,我省某市经过“调整水费听证会”后决定,2005年4月1日起,民用自来水水费调整为每立方米1.80元(含污染费),并提出“超额高费措施”,即每月用水量不超15m3收费,按规定标准1.80元/m3,若用水超过15m3,则超过部分按3.6元/m3收费(含“超标用水费”和“高额排污费”)
(1)小玲家响应市政府的号召,从2005年4月起计划平均每月用水量比过去平均每月用水量减少3m3,这使得小玲家现在用180m3的水比过去可多用3个月,问小玲家计划平均每月用水量是多少m3
(2)小玲家从2005年4月到2006年3月的一年中,有四个月因为有亲戚来家玩耍,这四个月用水量有二个月超计划平均用水量20%,有二个月超平均用水量的40%,其余八个月均按计划用水量用水,那么按新交费法,小玲家从2005年4月到2006年3月的这一年中应共交水费多少元?
21.如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.
(1)点Q的速度为 cm/s(用含x的代数式表示).
(2)求点P原来的速度.
22.列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
23.人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
24.阅读下面材料,解答后面的问题
解方程:.
解:设,则原方程化为:,方程两边同时乘y得:y2﹣4=0,
解得:y=±2,
经检验:y=±2都是方程的解,∴当y=2时,,解得:x=﹣1,
当y=﹣2时,,解得:x=,经检验:x=﹣1或x=都是原分式方程的解,
∴原分式方程的解为x=﹣1或 x=.上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程中,设,则原方程可化为: ;
(2)若在方程中,设,则原方程可化为: ;
(3)模仿上述换元法解方程:.
25.(换元法)解方程:(x2﹣3x)2﹣2(x2﹣3x)﹣8=0
解:设x2﹣3x=y则原方程可化为y2﹣2y﹣8=0
解得:y1=﹣2,y2=4
当y=﹣2时,x2﹣3x=﹣2,解得x1=2,x2=1
当y=4时,x2﹣3x=4,解得x1=4,x2=﹣1
∴原方程的根是x1=2,x2=1,x3=4,x4=﹣1,
根据以上材料,请解方程:
(1)(2x2﹣3x)2+5(2x2﹣3x)+4=0.
(2)x2﹣3x+5+=0
26.阅读下面材料,解答后面的问题
解方程:﹣=0.
解:设y=,则原方程化为:y﹣=0,
方程两边同时乘以y得:y2﹣4=0,解得:y=±2,
经检验:y=±2都是方程y﹣=0的解,
∴当y=2时,=2,解得:x=﹣1;当y=﹣2时,=﹣2,解得:x=,
经检验:x=﹣1或x=都是原分式方程的解,
∴原分式方程的解为x=﹣1或 x=.
上述这种解分式方程的方法称为换元法.
问题:(1)若在方程﹣=0中,设y=,则原方程可化为: ;
(2)模仿上述换元法解方程:﹣﹣1=0.
27.(1)若解关于x的分式方程+=会产生增根,求m的值.
(2)若方程=﹣1的解是正数,求a的取值范围.
28.已知关于x的方程+=3.
(1)当m取何值时,此方程的解为x=3;
(2)当m取何值时,此方程会产生增根;
(3)当此方程的解是正数时,求m的取值范围.
29.计算
(1)已知:,且2a﹣b+3c=23,求a,b,c的值.
(2)关于x的分式方程+=有增根,求k的值.
参考答案
1.C 2.D 3.B 4.D 5.B 6.A 7.D 8.D
9.④⑤⑥⑦⑨.
10.m>﹣6且m≠﹣3.
11.2或1.
12.﹣或﹣.
13.﹣1.
14..
15.解:(1)x+,其解为:x1=﹣4,x2=﹣5,
故答案为:x+=﹣9,x1=﹣4,x2=﹣5;
(2)x+=﹣(2n+1),其解为:x1=﹣n,x2=﹣n﹣1,
故答案为:x+=﹣(2n+1),x1=﹣n,x2=﹣n﹣1;
(3)x+=﹣2(n+2)
x+3+=﹣2(n+2)+3
(x+3)+=﹣(2n+1)
∴x+3=﹣n或x+3=﹣(n+1)
即:x1=﹣n﹣3,x2=﹣n﹣4.
16.解:(1),
分式方程的最简公分母为x(x+1),
方程两边都乘以x(x+1)得:
(x+1)2+5x2=6x(x+1),
化简得:4x=1,
解得:x=,
经检验,x=是原分式方程的解;
(2),
分式方程的最简公分母为(x+2)(x﹣2),
方程两边都乘以(x+2)(x﹣2)得:
(x﹣2)2﹣16=(x+2)2,
化简得:8x=﹣16,
解得:x=﹣2,
经检验x=﹣2是增根,原分式方程无解.
17.解:∵,
∴(x﹣2)(x﹣4)+2x=x+2,
∴x2﹣6x+8+2x=x+2,
x2﹣5x+6=0,
(x﹣2)(x﹣3)=0,
解得x1=2,x2=3,
检验:当x1=2时,x(x﹣2)(x+2)=0,是增根;
当x2=3时,x(x﹣2)(x+2)=15≠0,
∴x=3是原方程的解.
18.解:(1)设购买一个甲种足球需x元,则购买一个乙种足球需(x+20)元,
由,
解得:x=50
经检验x=50是原方程的解,
∴50+20=70元
答:购买一个甲种足球需50元,购买一个乙种足球需70元.
(2)设这所学校再次购买y个乙种足球,则购买(50﹣y)个甲种足球,50×(1+10%)×(50﹣y)+70y≤2900,
解得:y≤10,
由题意可得,最多可购买10个乙种足球.
答:这所学校最多可购买10个乙种足球.
19.解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要x天.根据题意,得 .
解得 x=90.
经检验,x=90是原方程的根.
∴x=×90=60.
答:甲、乙两队单独完成这项工程分别需60天和90天.
(2)设甲、乙两队合作完成这项工程需要y天,
则有 .
解得 y=36.
需要施工费用:36×(8.4+5.6)=504(万元).
∵504>500.
∴工程预算的施工费用不够用,需追加预算4万元.
20.解:(1)设小玲家计划平均每月用水量是xm3,则过去每月用水量为(x+3)m3,
由题意得,﹣=3,
解得:x=12或x=﹣15(不合题意,舍去),
经检验:x=12是原方程的解,
即小玲家计划平均每月用水量是12m3;
(2)计划用水量为12m3,
超过计划用水量20%时,用水量=12×(1+20%)=14.4m3,
超过计划用水量40%时,用水量=12×(1+40%)=16.8m3,
则应交水费:12×8×1.8+14.4×2×1.8+(15×1.8+1.8×3.6)×2=291.6(元).
答:小玲家从2005年4月到2006年3月的这一年中应共交水费291.6元.
21.解:(1)设点Q的速度为ycm/s,
由题意得3÷x=4÷y,
∴y=x,
故答案为:x;
(2)AC===5,
CD=5﹣1=4,
在B点处首次相遇后,点P的运动速度为(x+2)cm/s,
由题意得=,
解得:x=(cm/s),
经检验x=是原方程的根,
答:点P原来的速度为cm/s.
22.解:(1)设该商场第一批购进衬衫x件,则第二批购进衬衫2x件,
根据题意得:﹣=4,
解得:x=2000,
经检验,x=2000是所列分式方程的解,且符合题意.
答:商场第一批购进衬衫2000件.
(2)2000×2=4000(件),
(2000+4000﹣150)×58+150×58×0.8﹣80000﹣176000=90260(元).
答:售完这两批衬衫,商场共盈利90260元.
23.解:(1)设乙种牛奶的进价为x元/件,则甲种牛奶的进价为(x﹣5)元/件,
根据题意得:=,
解得:x=50,
经检验,x=50是原分式方程的解,且符合实际意义,
∴x﹣5=45.
答:乙种牛奶的进价是50元/件,甲种牛奶的进价是45元/件.
(2)设购进乙种牛奶y件,则购进甲种牛奶(3y﹣5)件,
根据题意得:(49﹣45)(3y﹣5)+(55﹣50)y=371,
解得:y=23,
∴3y﹣5=64.
答:该商场购进甲种牛奶64件,乙种牛奶23件.
24.解:(1)将代入原方程,则原方程化为;
(2)将代入方程,则原方程可化为;
(3)原方程化为:,
设,则原方程化为:,
方程两边同时乘y得:y2﹣1=0
解得:y=±1,
经检验:y=±1都是方程的解.
当y=1时,,该方程无解;
当y=﹣1时,,解得:;
经检验:是原分式方程的解,
∴原分式方程的解为.
25.解:(1)设2x2﹣3x=y,则原方程可化为y2+5y+4=0
解得:y1=﹣1,y2=﹣4
当y=﹣1时,2x2﹣3x=﹣1,解得x1=,x2=1
当y=﹣4时,2x2﹣3x=﹣4,方程无解
∴原方程的根是x1=,x2=1;
(2)设x2﹣3x=y,则原方程可化为y+5+=0
去分母,可得y2+5y+6=0
解得y1=﹣2,y2=﹣3
当y=﹣2时,x2﹣3x=﹣2,解得x1=2,x2=1
当y=﹣3时,x2﹣3x=﹣3,方程无解
经检验:x1=2,x2=1都是原方程的解
∴原方程的根是x1=2,x2=1.
26.解:(1)y﹣=0;
(2)原方程化为:﹣=0,
设y=,则原方程化为:y﹣=0,
方程两边同时乘以y得:y2﹣1=0,解得:y=±1,
经检验:y=±1都是方程y﹣=0的解.
当y=1时,=1,该方程无解;
当y=﹣1时,=﹣1,解得:x=﹣.
经检验:x=﹣是原分式方程的解,
∴原分式方程的解为x=﹣.
27.解:(1)方程两边都乘(x+2)(x﹣2),得
2(x+2)+mx=3(x﹣2)
∵最简公分母为(x+2)(x﹣2),
∴原方程增根为x=±2,
∴把x=2代入整式方程,得m=﹣4.
把x=﹣2代入整式方程,得m=6.
综上,可知m=﹣4或6.
(2)解:去分母,得2x+a=2﹣x
解得:x=,
∵解为正数,
∴,
∴2﹣a>0,
∴a<2,且x≠2,
∴a≠﹣4
∴a<2且a≠﹣4.
28.解:(1)把x=3代入方程+=3,得
m=﹣3;
(2)方程的增根为x=2,
2x+m=3x﹣6,
所以m=﹣4;
(3)去分母得,2x+m=3x﹣6,
解得x=m+6,
因为x>0,
所以m+6>0,
解得m>﹣6,
因为x≠2,
所以m≠﹣4.
29.解:(1)∵,
∴a+2=b,c+5=b,
∴a=b﹣2,c=b﹣5,
代入2a﹣b+3c=23得:2(b﹣2)﹣b+3(b﹣5)=23,
解得:b=,
∴a=,c=;
(2)+=
=,
去分母得:x+2+k(x﹣2)=4,
∵关于x的分式方程+=有增根,
∴x+2=0,x﹣2=0,
∴x=2或x=﹣2,
①当x=2时,代入x+2+k(x﹣2)=4得:2+2+k(2﹣2)=4,由于k的系数为0,等式恒成立,故k∈R;
②当x=﹣2时,代入x+2+k(x﹣2)=4得:﹣2+2+k(﹣2﹣2)=4,解得:k=﹣1,
综合上述:k为任何实数.
1.下列方程:①;②=2;③y=x;④=;⑤y+1=;⑥1+3(x﹣2)=7﹣x;⑦y2﹣3=.其中,分式方程有( )个.
A.1 B.2 C.3 D.4
2.若关于x的分式方程=2的解为非负数,则m的取值范围是( )
A.m>﹣1 B.m≥1 C.m>﹣1且m≠1 D.m≥﹣1且m≠1
3.甲乙两地相距300km,新修的高速公路开通后,在甲乙两地间行驶的长途客运车的平均速度提高了40%,而从甲乙两地的时间缩短了1.6h,试确定原来的车速.设原来的车速为xkm/h,下列列出的方程正确的是( )
A.=1.6 B.=1.6
C.=1.6 D.=1.6
4.几名同学包租一辆面包车去大山铺恐龙博物馆参观,面包车的租价为180元,出发时又增加了两名同学,结果每名同学比原来少摊了3元钱车费.设原来参加游览的同学供x名,则所列方程为( )
A. B.
C. D.
5.A地在河的上游,B地在河的下游,若船从A地开往B地的速度为V1,从B地返回A地的速度为V2,则A,B两地间往返一次的平均速度为( )
A. B.
C. D.无法计算
6.甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )
A.= B.=
C.= D.=
7.已知实数x满足x2++x﹣=4,则x﹣的值是( )
A.﹣2 B.1 C.﹣1或2 D.﹣2或1
8.分式方程=有增根,则m的值为( )
A.0和3 B.1 C.1和﹣2 D.3
9.下列方程是关于x的方程,其中是分式方程的是 (只填序号)
①=5;②+2=;③;④;⑤1+=2﹣;⑥;⑦;⑧;⑨.
10.关于x的分式方程的解为正数,则m的取值范围是 .
11.若关于x的方程=+1无解,则a的值是 .
12.若关于x的分式方程﹣1=无解,则m的值 .
13.若x为实数,且+x2+2x=﹣2,则x2+2x的值为 .
14.某市为治理污水,需要铺设一段全长600m的污水排放管道,铺设120m后,为加快施工进度,后来每天比原计划增加20m,结果共用11天完成这一任务,求原计划每天铺设管道的长度.如果设原计划每天铺设xm管道,那么根据题意,可列方程 .
15.观察下列方程的特征及其解的特点;
①x+=﹣3的解为x1=﹣1,x2=﹣2.
②x+=﹣5的解为x1=﹣2,x2=﹣3.
③x+=﹣7的解为x1=﹣3,x2=﹣4;
解答下列问题;
(1)请你写出一个符合上述特征的方程为 ,其解为 .
(2)根据这类方程特征,写出第n个方程为 ,其解为 .
(3)请利用(2)的结论,求关于x的方程x+=﹣2(n+2)(其中n为正整数)的解.
16.解分式方程.
(1) (2).
17.解方程:.
18.昆明市某学校2018年在商场购买甲、乙两种不同的足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球的数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球,一个乙种足球各需多少元?
(2)为响应习总书记“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对甲种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,如果此次购买甲、乙两种足球的费用不超过2900元,那么这所学校最多可购买多少个乙种足球?
19.京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
20.为了保护水资源,实行节约用水,我省某市经过“调整水费听证会”后决定,2005年4月1日起,民用自来水水费调整为每立方米1.80元(含污染费),并提出“超额高费措施”,即每月用水量不超15m3收费,按规定标准1.80元/m3,若用水超过15m3,则超过部分按3.6元/m3收费(含“超标用水费”和“高额排污费”)
(1)小玲家响应市政府的号召,从2005年4月起计划平均每月用水量比过去平均每月用水量减少3m3,这使得小玲家现在用180m3的水比过去可多用3个月,问小玲家计划平均每月用水量是多少m3
(2)小玲家从2005年4月到2006年3月的一年中,有四个月因为有亲戚来家玩耍,这四个月用水量有二个月超计划平均用水量20%,有二个月超平均用水量的40%,其余八个月均按计划用水量用水,那么按新交费法,小玲家从2005年4月到2006年3月的这一年中应共交水费多少元?
21.如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.
(1)点Q的速度为 cm/s(用含x的代数式表示).
(2)求点P原来的速度.
22.列方程解应用题:
某商场用8万元购进一批新款衬衫,上架后很快销售一空,商场又紧急购进第二批这种衬衫,数量是第一次的2倍,但进价涨了4元/件,结果共用去17.6万元.
(1)该商场第一批购进衬衫多少件?
(2)商场销售这种衬衫时,每件定价都是58元,剩至150件时按八折出售,全部售完.售完这两批衬衫,商场共盈利多少元?
23.人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
24.阅读下面材料,解答后面的问题
解方程:.
解:设,则原方程化为:,方程两边同时乘y得:y2﹣4=0,
解得:y=±2,
经检验:y=±2都是方程的解,∴当y=2时,,解得:x=﹣1,
当y=﹣2时,,解得:x=,经检验:x=﹣1或x=都是原分式方程的解,
∴原分式方程的解为x=﹣1或 x=.上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程中,设,则原方程可化为: ;
(2)若在方程中,设,则原方程可化为: ;
(3)模仿上述换元法解方程:.
25.(换元法)解方程:(x2﹣3x)2﹣2(x2﹣3x)﹣8=0
解:设x2﹣3x=y则原方程可化为y2﹣2y﹣8=0
解得:y1=﹣2,y2=4
当y=﹣2时,x2﹣3x=﹣2,解得x1=2,x2=1
当y=4时,x2﹣3x=4,解得x1=4,x2=﹣1
∴原方程的根是x1=2,x2=1,x3=4,x4=﹣1,
根据以上材料,请解方程:
(1)(2x2﹣3x)2+5(2x2﹣3x)+4=0.
(2)x2﹣3x+5+=0
26.阅读下面材料,解答后面的问题
解方程:﹣=0.
解:设y=,则原方程化为:y﹣=0,
方程两边同时乘以y得:y2﹣4=0,解得:y=±2,
经检验:y=±2都是方程y﹣=0的解,
∴当y=2时,=2,解得:x=﹣1;当y=﹣2时,=﹣2,解得:x=,
经检验:x=﹣1或x=都是原分式方程的解,
∴原分式方程的解为x=﹣1或 x=.
上述这种解分式方程的方法称为换元法.
问题:(1)若在方程﹣=0中,设y=,则原方程可化为: ;
(2)模仿上述换元法解方程:﹣﹣1=0.
27.(1)若解关于x的分式方程+=会产生增根,求m的值.
(2)若方程=﹣1的解是正数,求a的取值范围.
28.已知关于x的方程+=3.
(1)当m取何值时,此方程的解为x=3;
(2)当m取何值时,此方程会产生增根;
(3)当此方程的解是正数时,求m的取值范围.
29.计算
(1)已知:,且2a﹣b+3c=23,求a,b,c的值.
(2)关于x的分式方程+=有增根,求k的值.
参考答案
1.C 2.D 3.B 4.D 5.B 6.A 7.D 8.D
9.④⑤⑥⑦⑨.
10.m>﹣6且m≠﹣3.
11.2或1.
12.﹣或﹣.
13.﹣1.
14..
15.解:(1)x+,其解为:x1=﹣4,x2=﹣5,
故答案为:x+=﹣9,x1=﹣4,x2=﹣5;
(2)x+=﹣(2n+1),其解为:x1=﹣n,x2=﹣n﹣1,
故答案为:x+=﹣(2n+1),x1=﹣n,x2=﹣n﹣1;
(3)x+=﹣2(n+2)
x+3+=﹣2(n+2)+3
(x+3)+=﹣(2n+1)
∴x+3=﹣n或x+3=﹣(n+1)
即:x1=﹣n﹣3,x2=﹣n﹣4.
16.解:(1),
分式方程的最简公分母为x(x+1),
方程两边都乘以x(x+1)得:
(x+1)2+5x2=6x(x+1),
化简得:4x=1,
解得:x=,
经检验,x=是原分式方程的解;
(2),
分式方程的最简公分母为(x+2)(x﹣2),
方程两边都乘以(x+2)(x﹣2)得:
(x﹣2)2﹣16=(x+2)2,
化简得:8x=﹣16,
解得:x=﹣2,
经检验x=﹣2是增根,原分式方程无解.
17.解:∵,
∴(x﹣2)(x﹣4)+2x=x+2,
∴x2﹣6x+8+2x=x+2,
x2﹣5x+6=0,
(x﹣2)(x﹣3)=0,
解得x1=2,x2=3,
检验:当x1=2时,x(x﹣2)(x+2)=0,是增根;
当x2=3时,x(x﹣2)(x+2)=15≠0,
∴x=3是原方程的解.
18.解:(1)设购买一个甲种足球需x元,则购买一个乙种足球需(x+20)元,
由,
解得:x=50
经检验x=50是原方程的解,
∴50+20=70元
答:购买一个甲种足球需50元,购买一个乙种足球需70元.
(2)设这所学校再次购买y个乙种足球,则购买(50﹣y)个甲种足球,50×(1+10%)×(50﹣y)+70y≤2900,
解得:y≤10,
由题意可得,最多可购买10个乙种足球.
答:这所学校最多可购买10个乙种足球.
19.解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要x天.根据题意,得 .
解得 x=90.
经检验,x=90是原方程的根.
∴x=×90=60.
答:甲、乙两队单独完成这项工程分别需60天和90天.
(2)设甲、乙两队合作完成这项工程需要y天,
则有 .
解得 y=36.
需要施工费用:36×(8.4+5.6)=504(万元).
∵504>500.
∴工程预算的施工费用不够用,需追加预算4万元.
20.解:(1)设小玲家计划平均每月用水量是xm3,则过去每月用水量为(x+3)m3,
由题意得,﹣=3,
解得:x=12或x=﹣15(不合题意,舍去),
经检验:x=12是原方程的解,
即小玲家计划平均每月用水量是12m3;
(2)计划用水量为12m3,
超过计划用水量20%时,用水量=12×(1+20%)=14.4m3,
超过计划用水量40%时,用水量=12×(1+40%)=16.8m3,
则应交水费:12×8×1.8+14.4×2×1.8+(15×1.8+1.8×3.6)×2=291.6(元).
答:小玲家从2005年4月到2006年3月的这一年中应共交水费291.6元.
21.解:(1)设点Q的速度为ycm/s,
由题意得3÷x=4÷y,
∴y=x,
故答案为:x;
(2)AC===5,
CD=5﹣1=4,
在B点处首次相遇后,点P的运动速度为(x+2)cm/s,
由题意得=,
解得:x=(cm/s),
经检验x=是原方程的根,
答:点P原来的速度为cm/s.
22.解:(1)设该商场第一批购进衬衫x件,则第二批购进衬衫2x件,
根据题意得:﹣=4,
解得:x=2000,
经检验,x=2000是所列分式方程的解,且符合题意.
答:商场第一批购进衬衫2000件.
(2)2000×2=4000(件),
(2000+4000﹣150)×58+150×58×0.8﹣80000﹣176000=90260(元).
答:售完这两批衬衫,商场共盈利90260元.
23.解:(1)设乙种牛奶的进价为x元/件,则甲种牛奶的进价为(x﹣5)元/件,
根据题意得:=,
解得:x=50,
经检验,x=50是原分式方程的解,且符合实际意义,
∴x﹣5=45.
答:乙种牛奶的进价是50元/件,甲种牛奶的进价是45元/件.
(2)设购进乙种牛奶y件,则购进甲种牛奶(3y﹣5)件,
根据题意得:(49﹣45)(3y﹣5)+(55﹣50)y=371,
解得:y=23,
∴3y﹣5=64.
答:该商场购进甲种牛奶64件,乙种牛奶23件.
24.解:(1)将代入原方程,则原方程化为;
(2)将代入方程,则原方程可化为;
(3)原方程化为:,
设,则原方程化为:,
方程两边同时乘y得:y2﹣1=0
解得:y=±1,
经检验:y=±1都是方程的解.
当y=1时,,该方程无解;
当y=﹣1时,,解得:;
经检验:是原分式方程的解,
∴原分式方程的解为.
25.解:(1)设2x2﹣3x=y,则原方程可化为y2+5y+4=0
解得:y1=﹣1,y2=﹣4
当y=﹣1时,2x2﹣3x=﹣1,解得x1=,x2=1
当y=﹣4时,2x2﹣3x=﹣4,方程无解
∴原方程的根是x1=,x2=1;
(2)设x2﹣3x=y,则原方程可化为y+5+=0
去分母,可得y2+5y+6=0
解得y1=﹣2,y2=﹣3
当y=﹣2时,x2﹣3x=﹣2,解得x1=2,x2=1
当y=﹣3时,x2﹣3x=﹣3,方程无解
经检验:x1=2,x2=1都是原方程的解
∴原方程的根是x1=2,x2=1.
26.解:(1)y﹣=0;
(2)原方程化为:﹣=0,
设y=,则原方程化为:y﹣=0,
方程两边同时乘以y得:y2﹣1=0,解得:y=±1,
经检验:y=±1都是方程y﹣=0的解.
当y=1时,=1,该方程无解;
当y=﹣1时,=﹣1,解得:x=﹣.
经检验:x=﹣是原分式方程的解,
∴原分式方程的解为x=﹣.
27.解:(1)方程两边都乘(x+2)(x﹣2),得
2(x+2)+mx=3(x﹣2)
∵最简公分母为(x+2)(x﹣2),
∴原方程增根为x=±2,
∴把x=2代入整式方程,得m=﹣4.
把x=﹣2代入整式方程,得m=6.
综上,可知m=﹣4或6.
(2)解:去分母,得2x+a=2﹣x
解得:x=,
∵解为正数,
∴,
∴2﹣a>0,
∴a<2,且x≠2,
∴a≠﹣4
∴a<2且a≠﹣4.
28.解:(1)把x=3代入方程+=3,得
m=﹣3;
(2)方程的增根为x=2,
2x+m=3x﹣6,
所以m=﹣4;
(3)去分母得,2x+m=3x﹣6,
解得x=m+6,
因为x>0,
所以m+6>0,
解得m>﹣6,
因为x≠2,
所以m≠﹣4.
29.解:(1)∵,
∴a+2=b,c+5=b,
∴a=b﹣2,c=b﹣5,
代入2a﹣b+3c=23得:2(b﹣2)﹣b+3(b﹣5)=23,
解得:b=,
∴a=,c=;
(2)+=
=,
去分母得:x+2+k(x﹣2)=4,
∵关于x的分式方程+=有增根,
∴x+2=0,x﹣2=0,
∴x=2或x=﹣2,
①当x=2时,代入x+2+k(x﹣2)=4得:2+2+k(2﹣2)=4,由于k的系数为0,等式恒成立,故k∈R;
②当x=﹣2时,代入x+2+k(x﹣2)=4得:﹣2+2+k(﹣2﹣2)=4,解得:k=﹣1,
综合上述:k为任何实数.
