2022—2023学年人教版数学八年级上册11.3.1 多边形 导学案(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.3.1 多边形 导学案(含答案) | 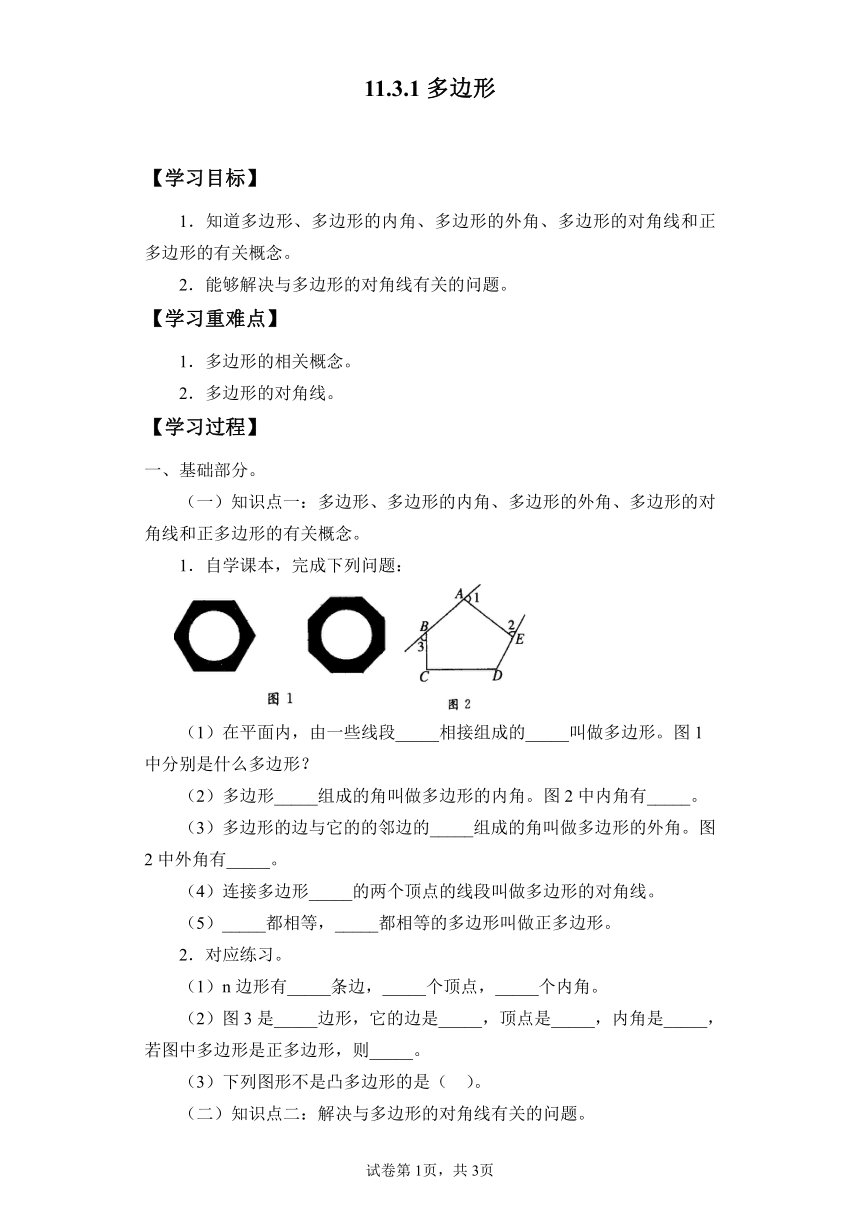 | |
| 格式 | zip | ||
| 文件大小 | 56.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 17:13:36 | ||
图片预览


文档简介
11.3.1多边形
【学习目标】
1.知道多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念。
2.能够解决与多边形的对角线有关的问题。
【学习重难点】
1.多边形的相关概念。
2.多边形的对角线。
【学习过程】
一、基础部分。
(一)知识点一:多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念。
1.自学课本,完成下列问题:
(1)在平面内,由一些线段_____相接组成的_____叫做多边形。图1中分别是什么多边形?
(2)多边形_____组成的角叫做多边形的内角。图2中内角有_____。
(3)多边形的边与它的的邻边的_____组成的角叫做多边形的外角。图2中外角有_____。
(4)连接多边形_____的两个顶点的线段叫做多边形的对角线。
(5)_____都相等,_____都相等的多边形叫做正多边形。
2.对应练习。
(1)n边形有_____条边,_____个顶点,_____个内角。
(2)图3是_____边形,它的边是_____,顶点是_____,内角是_____,若图中多边形是正多边形,则_____。
(3)下列图形不是凸多边形的是( )。
(二)知识点二:解决与多边形的对角线有关的问题。
1.探究:画出下列多边形的对角线。回答问题:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了_____个三角形;四边形共有_____条对角线。
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了_____个三角形;五边形共有_____条对角线。
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了_____个三角形;六边形共有_____条对角线。
(4)猜想:①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了_____个三角形;100边形共有_____条对角线.②从n边形的一个顶点出发可以画_____条对角线,把n分成了_____个三角形;n边形共有_____条对角线。
2.对应练习:
(1)从n边形的一个顶点出发可作_____条对角线,从n边形n个顶点出发可作_____条对角线,除去重复作的对角线,则n边形的对角线的总数为_____条。
(2)过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则(m-k)=_____。
(3)过十边形的一个顶点可作出几条对角线?把十边形分成了几个三角形?
(4)十二边形共有_____条对角线,过一个顶点可作_____条对角线,可把十二边形分成_____个三角形。
二、拓展部分。
1.一个八边形的所有对角线的条数是( )
A.5 B.20 C.22 D.18
2.在四边形ABCD中,的对角是( )
A. B. C. D.
3.下列说法中,正确的有( )
①由几条线段连接起来组成的图形叫多边形;
②三角形是边数最少的多边形;
③n边形有n条边、n个顶点.
A.0个 B.1个 C.2个 D.3个
4.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
5.一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为( )
A.15或16或17 B.15或17 C.16或17 D.16或17或18
6.过某个多边形的一个顶点的所有对角线,将这个多边形分成2020个三角形,则这个多边形的边数为_________.
7.从六边形的一个顶点出发,可以画出条对角线,它们将六边形分成个三角形.边形没有对角线,则的值为______.
8.正多边形的一个外角是40°,则这个正多边形从一个顶点出发有__条对角线.
9.四边形共有几条对角线?五边形呢?n边形呢?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.C
3.C
4.A
5.A
6.2022
7.10
8.6
9.2,5,.
1 / 3
【学习目标】
1.知道多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念。
2.能够解决与多边形的对角线有关的问题。
【学习重难点】
1.多边形的相关概念。
2.多边形的对角线。
【学习过程】
一、基础部分。
(一)知识点一:多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念。
1.自学课本,完成下列问题:
(1)在平面内,由一些线段_____相接组成的_____叫做多边形。图1中分别是什么多边形?
(2)多边形_____组成的角叫做多边形的内角。图2中内角有_____。
(3)多边形的边与它的的邻边的_____组成的角叫做多边形的外角。图2中外角有_____。
(4)连接多边形_____的两个顶点的线段叫做多边形的对角线。
(5)_____都相等,_____都相等的多边形叫做正多边形。
2.对应练习。
(1)n边形有_____条边,_____个顶点,_____个内角。
(2)图3是_____边形,它的边是_____,顶点是_____,内角是_____,若图中多边形是正多边形,则_____。
(3)下列图形不是凸多边形的是( )。
(二)知识点二:解决与多边形的对角线有关的问题。
1.探究:画出下列多边形的对角线。回答问题:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了_____个三角形;四边形共有_____条对角线。
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了_____个三角形;五边形共有_____条对角线。
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了_____个三角形;六边形共有_____条对角线。
(4)猜想:①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了_____个三角形;100边形共有_____条对角线.②从n边形的一个顶点出发可以画_____条对角线,把n分成了_____个三角形;n边形共有_____条对角线。
2.对应练习:
(1)从n边形的一个顶点出发可作_____条对角线,从n边形n个顶点出发可作_____条对角线,除去重复作的对角线,则n边形的对角线的总数为_____条。
(2)过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则(m-k)=_____。
(3)过十边形的一个顶点可作出几条对角线?把十边形分成了几个三角形?
(4)十二边形共有_____条对角线,过一个顶点可作_____条对角线,可把十二边形分成_____个三角形。
二、拓展部分。
1.一个八边形的所有对角线的条数是( )
A.5 B.20 C.22 D.18
2.在四边形ABCD中,的对角是( )
A. B. C. D.
3.下列说法中,正确的有( )
①由几条线段连接起来组成的图形叫多边形;
②三角形是边数最少的多边形;
③n边形有n条边、n个顶点.
A.0个 B.1个 C.2个 D.3个
4.将一个四边形截去一个角后,它不可能是( )
A.六边形 B.五边形 C.四边形 D.三角形
5.一个多边形截去一个角后,变成16边形,那么原来的多边形的边数为( )
A.15或16或17 B.15或17 C.16或17 D.16或17或18
6.过某个多边形的一个顶点的所有对角线,将这个多边形分成2020个三角形,则这个多边形的边数为_________.
7.从六边形的一个顶点出发,可以画出条对角线,它们将六边形分成个三角形.边形没有对角线,则的值为______.
8.正多边形的一个外角是40°,则这个正多边形从一个顶点出发有__条对角线.
9.四边形共有几条对角线?五边形呢?n边形呢?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.C
3.C
4.A
5.A
6.2022
7.10
8.6
9.2,5,.
1 / 3
