2022—2023学年人教版数学八年级上册11.3.2多边形的内角和 导学案 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.3.2多边形的内角和 导学案 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 59.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 17:17:25 | ||
图片预览

文档简介
11.3.2多边形的内角和
【学习目标】
1.知道多边形的内角和与外角和定理。
2.运用多边形内角和与外角和定理进行有关的计算。
【学习重难点】
1.多边形的内角和与外角和定理。
2.内角和定理的推导。
【学习过程】
一、基础部分。
(一)学前准备。
1.三角形的内角和是多少?_____
2.正方形、长方形的内角和是多少?_____
3.从n边形的一个顶点出发可以画_____条对角线,把n边形分成了_____个三角形。
(二)探索思考。
1.知识点一:多边形的内角和定理。
探究1:任意画一个四边形,量出它的4个内角,计算它们的和。再画几个四边形,量一量、算一算。你能得出什么结论?能否利用三角形内角和等于180°得出这个结论?
探究2:从上面的问题,你能想出五边形和六边形的内角和各是多少吗?
观察下图,请填空:
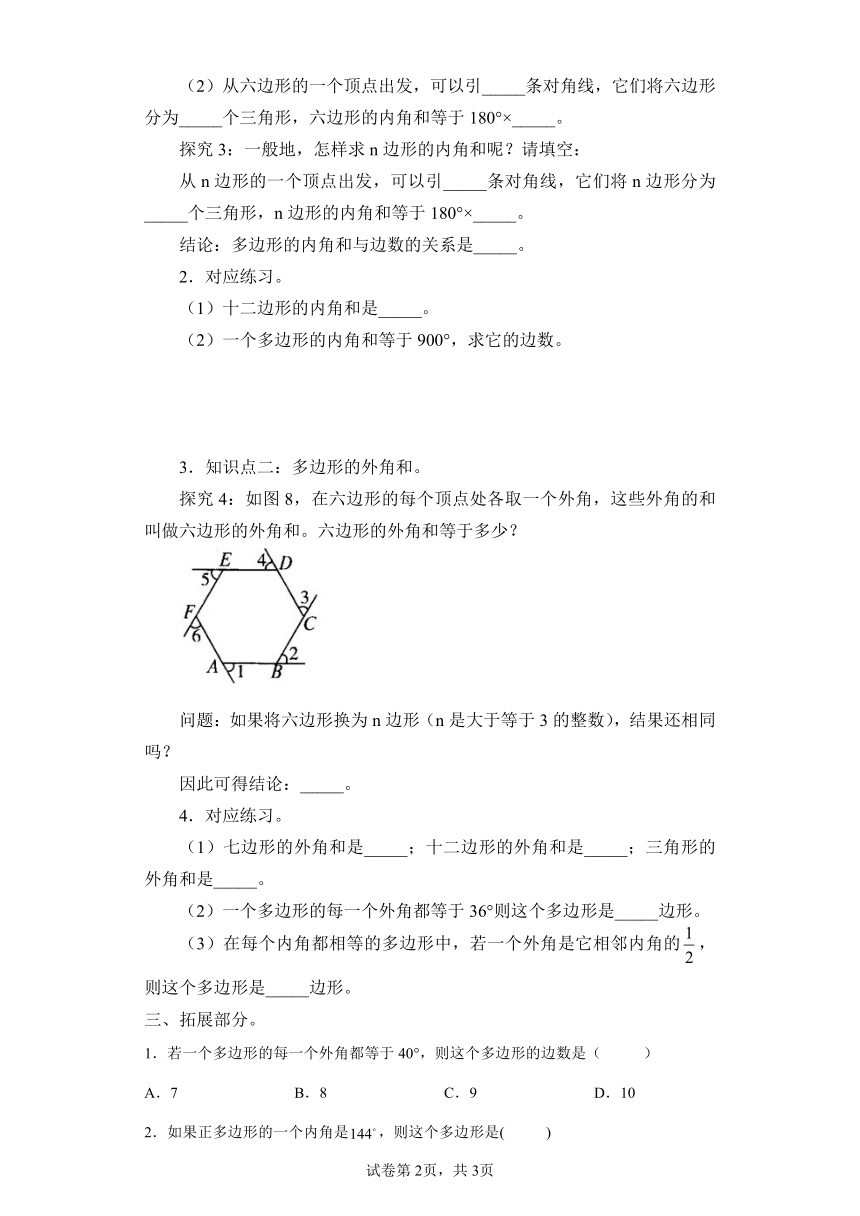
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×_____。
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×_____。
探究3:一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引_____条对角线,它们将n边形分为_____个三角形,n边形的内角和等于180°×_____。
结论:多边形的内角和与边数的关系是_____。
2.对应练习。
(1)十二边形的内角和是_____。
(2)一个多边形的内角和等于900°,求它的边数。
3.知识点二:多边形的外角和。
探究4:如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
问题:如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论:_____。
4.对应练习。
(1)七边形的外角和是_____;十二边形的外角和是_____;三角形的外角和是_____。
(2)一个多边形的每一个外角都等于36°则这个多边形是_____边形。
(3)在每个内角都相等的多边形中,若一个外角是它相邻内角的,则这个多边形是_____边形。
三、拓展部分。
1.若一个多边形的每一个外角都等于40°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
2.如果正多边形的一个内角是,则这个多边形是( )
A.正十边形 B.正九边形 C.正八边形 D.正七边形
3.下列说法中,正确的个数有( )
①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°;
③三角形的外角大于与它不相邻的任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;
A.1个 B.2个 C.3个 D.4
4.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
5.能够铺满地面的正多边形组合是( )
A.正三角形和正五边形 B.正方形和正六边形
C.正方形和正八边形 D.正五边形和正十边形
6.如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ACB=_______度.
7.一个多边形除了一个内角之外,其余各内角的度数和为1510°,则这个多边形的边数为 _____.
8.剪纸片:有一张长方形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片:从这3张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有4张纸片;……;如此下去,若最后得到10张纸片,其中有1张五边形纸片,3张三角形纸片,5 张四边形纸片,则还有一张多边形纸片的边数为________.
9.多边形的内角和与某一个外角的度数和为1350度.
(1)求多边形的边数;
(2)此多边形必有一内角为多少度?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.C
5.C
6.60
7.11
8.6
9.(1)九边形(2)90°
1 / 3
【学习目标】
1.知道多边形的内角和与外角和定理。
2.运用多边形内角和与外角和定理进行有关的计算。
【学习重难点】
1.多边形的内角和与外角和定理。
2.内角和定理的推导。
【学习过程】
一、基础部分。
(一)学前准备。
1.三角形的内角和是多少?_____
2.正方形、长方形的内角和是多少?_____
3.从n边形的一个顶点出发可以画_____条对角线,把n边形分成了_____个三角形。
(二)探索思考。
1.知识点一:多边形的内角和定理。
探究1:任意画一个四边形,量出它的4个内角,计算它们的和。再画几个四边形,量一量、算一算。你能得出什么结论?能否利用三角形内角和等于180°得出这个结论?
探究2:从上面的问题,你能想出五边形和六边形的内角和各是多少吗?
观察下图,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×_____。
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×_____。
探究3:一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引_____条对角线,它们将n边形分为_____个三角形,n边形的内角和等于180°×_____。
结论:多边形的内角和与边数的关系是_____。
2.对应练习。
(1)十二边形的内角和是_____。
(2)一个多边形的内角和等于900°,求它的边数。
3.知识点二:多边形的外角和。
探究4:如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
问题:如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论:_____。
4.对应练习。
(1)七边形的外角和是_____;十二边形的外角和是_____;三角形的外角和是_____。
(2)一个多边形的每一个外角都等于36°则这个多边形是_____边形。
(3)在每个内角都相等的多边形中,若一个外角是它相邻内角的,则这个多边形是_____边形。
三、拓展部分。
1.若一个多边形的每一个外角都等于40°,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
2.如果正多边形的一个内角是,则这个多边形是( )
A.正十边形 B.正九边形 C.正八边形 D.正七边形
3.下列说法中,正确的个数有( )
①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°;
③三角形的外角大于与它不相邻的任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°;
A.1个 B.2个 C.3个 D.4
4.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
5.能够铺满地面的正多边形组合是( )
A.正三角形和正五边形 B.正方形和正六边形
C.正方形和正八边形 D.正五边形和正十边形
6.如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ACB=_______度.
7.一个多边形除了一个内角之外,其余各内角的度数和为1510°,则这个多边形的边数为 _____.
8.剪纸片:有一张长方形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片:从这3张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有4张纸片;……;如此下去,若最后得到10张纸片,其中有1张五边形纸片,3张三角形纸片,5 张四边形纸片,则还有一张多边形纸片的边数为________.
9.多边形的内角和与某一个外角的度数和为1350度.
(1)求多边形的边数;
(2)此多边形必有一内角为多少度?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.C
5.C
6.60
7.11
8.6
9.(1)九边形(2)90°
1 / 3
