2022--2023学年人教版九年级数学上册22.2 二次函数与一元二次方程 导学案(含答案)
文档属性
| 名称 | 2022--2023学年人教版九年级数学上册22.2 二次函数与一元二次方程 导学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览

文档简介
22.2二次函数与一元二次方程
【学习目标】
1.使学生掌握二次函数与x轴交点个数的判断方法。
2.理解二次函数与x轴交点的横坐标与一元二次方程ax2+bx+c=0根的关系。
【学习重难点】
二次函数与x轴交点的横坐标与一元二次方程ax2+bx+c=0根的关系。
【学习过程】
一、习题导入。
1.解下列一元二次方程。
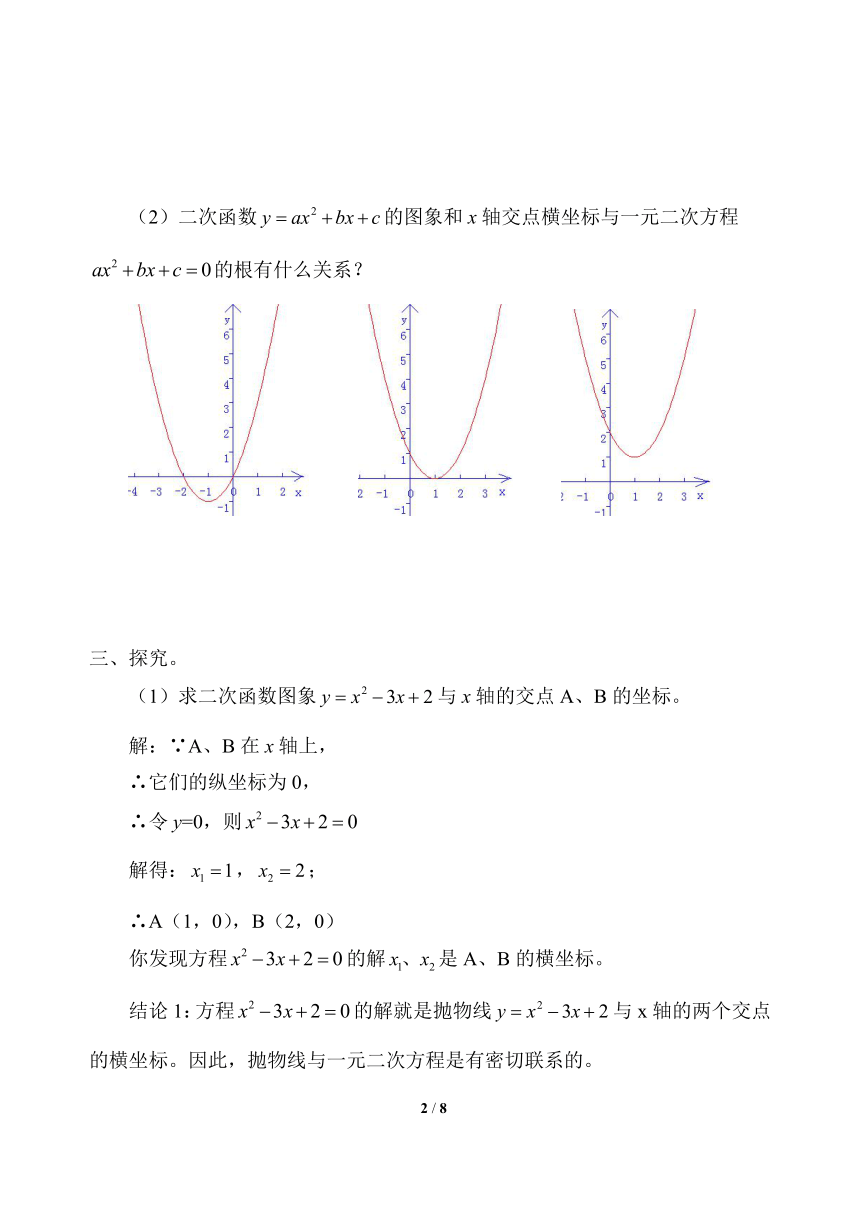
2.(1)二次函数,,的图象如图示。
每个图象与x轴有几个交点?
(2)二次函数的图象和x轴交点横坐标与一元二次方程的根有什么关系?
三、探究。
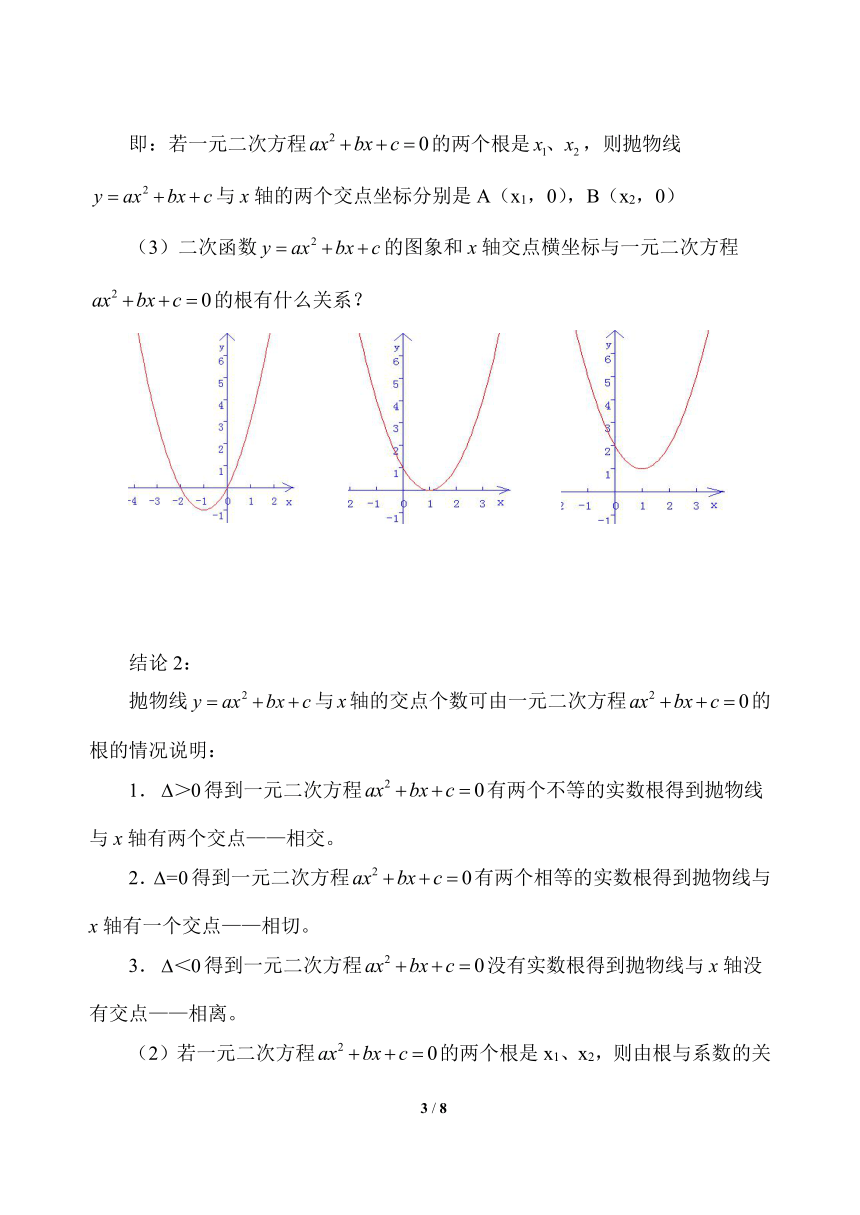
(1)求二次函数图象与x轴的交点A、B的坐标。
解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则
解得:,;
∴A(1,0),B(2,0)
你发现方程的解是A、B的横坐标。
结论1:方程的解就是抛物线与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。
即:若一元二次方程的两个根是,则抛物线与x轴的两个交点坐标分别是A(x1,0),B(x2,0)
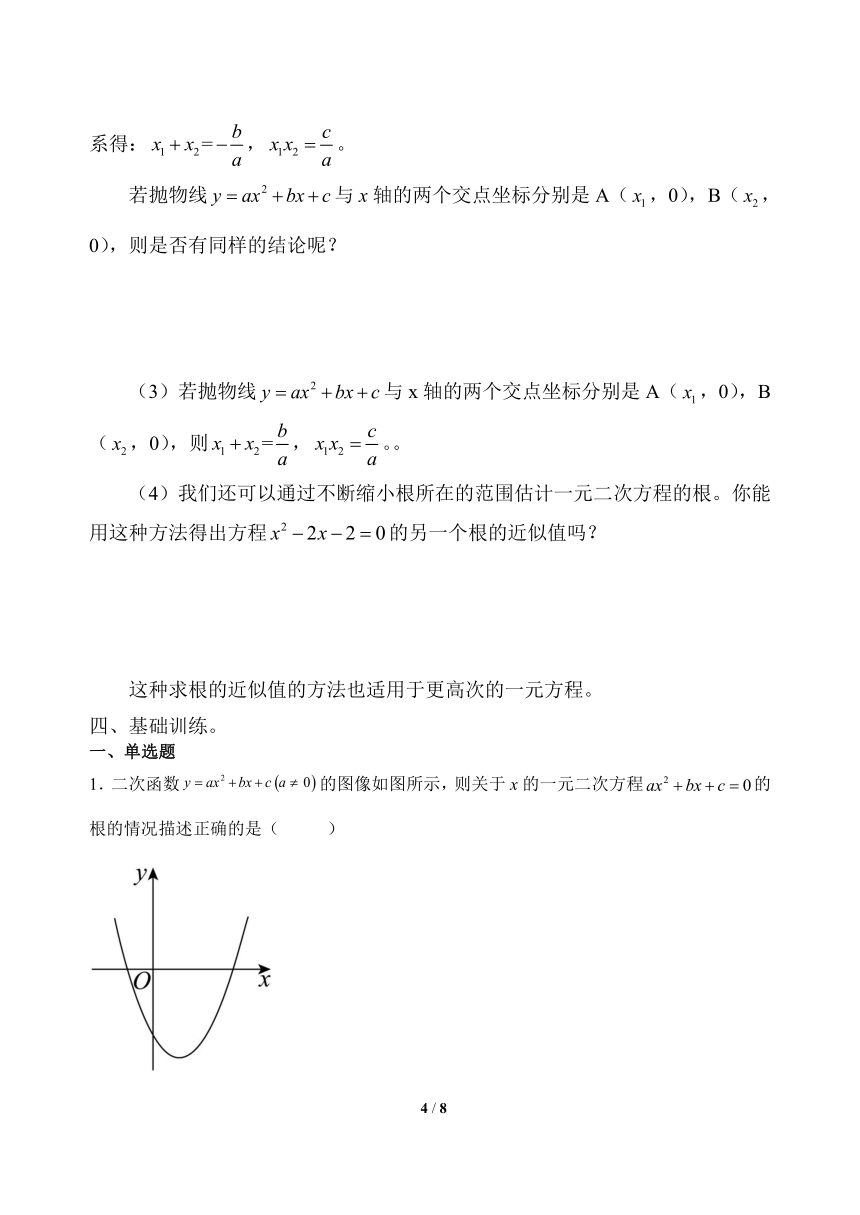
(3)二次函数的图象和x轴交点横坐标与一元二次方程的根有什么关系?
结论2:
抛物线与x轴的交点个数可由一元二次方程的根的情况说明:
1.得到一元二次方程有两个不等的实数根得到抛物线与x轴有两个交点——相交。
2.得到一元二次方程有两个相等的实数根得到抛物线与x轴有一个交点——相切。
3.得到一元二次方程没有实数根得到抛物线与x轴没有交点——相离。
(2)若一元二次方程的两个根是x1、x2,则由根与系数的关系得:,。
若抛物线与x轴的两个交点坐标分别是A(,0),B(,0),则是否有同样的结论呢?
(3)若抛物线与x轴的两个交点坐标分别是A(,0),B(,0),则,。。
(4)我们还可以通过不断缩小根所在的范围估计一元二次方程的根。你能用这种方法得出方程的另一个根的近似值吗?
这种求根的近似值的方法也适用于更高次的一元方程。
四、基础训练。
一、单选题
1.二次函数的图像如图所示,则关于x的一元二次方程的根的情况描述正确的是( )
A.有两个相等的实数根 B.有两个异号的实数根
C.有两个同号的实数根 D.有两个无法确定符号的实数根
2.小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1 C.x=-4 D.x=-1或x=4
3.已知二次函数的顶点为(1,5),那么关于x的一元二次方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根 C.没有实数根 D.无法确定
4.已知函数y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围是( )
A. B. C.且k≠0 D.且k≠0
5.如图,抛物线(是常数,)与轴交于两点,顶点给出下列结论:①;②若在抛物线上,则;③关于的方程有实数解,则;④当时,为等腰直角三角形,其中正确的结论是( )
A.①② B.①③ C.②③ D.②④
二、填空题
6.若一元二次方程(b,c为常数)的两根满足,则符合条件的一个方程为_____.
7.试写出一个二次函数关系式,使它对应的一元二次方程的一个根为0,另一个根在1到2之间:________.
8.如图,在平面直角坐标系中,抛物线(m为常数,且)与直线y=2交于A、B两点.若AB=2,则m的值为______.
三、解答题
9.(1)若将y=x2﹣x﹣图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
(2)根据图象,写出当y>0时,x的取值范围.
10.已知二次函数表达式为y=x2-4x+1.
(1)求出这个二次函数图象的对称轴;
(2)求出这个二次函数的图象与坐标轴的交点坐标.
11.设二次函数(a,b是常数,),部分对应值如下表:
… …
… …
(1)试判断该函数图象的开口方向;
(2)当时,求函数y的值;
(3)根据你的解题经验,直接写出的解.
参考答案:
1.B
2.D
3.A
4.B
5.D
6.(答案不唯一)
7.
8.
9.(1)y=x2+x﹣ ;(2)x<﹣1或x>3
10.(1)直线x=2
(2)与x轴的交点坐标为(2+,0)和(2-,0),与y轴的交点坐标为(0,1)
11.(1)抛物线开口向上
(2)
(3)
5 / 6
【学习目标】
1.使学生掌握二次函数与x轴交点个数的判断方法。
2.理解二次函数与x轴交点的横坐标与一元二次方程ax2+bx+c=0根的关系。
【学习重难点】
二次函数与x轴交点的横坐标与一元二次方程ax2+bx+c=0根的关系。
【学习过程】
一、习题导入。
1.解下列一元二次方程。
2.(1)二次函数,,的图象如图示。
每个图象与x轴有几个交点?
(2)二次函数的图象和x轴交点横坐标与一元二次方程的根有什么关系?
三、探究。
(1)求二次函数图象与x轴的交点A、B的坐标。
解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则
解得:,;
∴A(1,0),B(2,0)
你发现方程的解是A、B的横坐标。
结论1:方程的解就是抛物线与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。
即:若一元二次方程的两个根是,则抛物线与x轴的两个交点坐标分别是A(x1,0),B(x2,0)
(3)二次函数的图象和x轴交点横坐标与一元二次方程的根有什么关系?
结论2:
抛物线与x轴的交点个数可由一元二次方程的根的情况说明:
1.得到一元二次方程有两个不等的实数根得到抛物线与x轴有两个交点——相交。
2.得到一元二次方程有两个相等的实数根得到抛物线与x轴有一个交点——相切。
3.得到一元二次方程没有实数根得到抛物线与x轴没有交点——相离。
(2)若一元二次方程的两个根是x1、x2,则由根与系数的关系得:,。
若抛物线与x轴的两个交点坐标分别是A(,0),B(,0),则是否有同样的结论呢?
(3)若抛物线与x轴的两个交点坐标分别是A(,0),B(,0),则,。。
(4)我们还可以通过不断缩小根所在的范围估计一元二次方程的根。你能用这种方法得出方程的另一个根的近似值吗?
这种求根的近似值的方法也适用于更高次的一元方程。
四、基础训练。
一、单选题
1.二次函数的图像如图所示,则关于x的一元二次方程的根的情况描述正确的是( )
A.有两个相等的实数根 B.有两个异号的实数根
C.有两个同号的实数根 D.有两个无法确定符号的实数根
2.小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1 C.x=-4 D.x=-1或x=4
3.已知二次函数的顶点为(1,5),那么关于x的一元二次方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根 C.没有实数根 D.无法确定
4.已知函数y=kx2﹣7x﹣7的图象和x轴有交点,则k的取值范围是( )
A. B. C.且k≠0 D.且k≠0
5.如图,抛物线(是常数,)与轴交于两点,顶点给出下列结论:①;②若在抛物线上,则;③关于的方程有实数解,则;④当时,为等腰直角三角形,其中正确的结论是( )
A.①② B.①③ C.②③ D.②④
二、填空题
6.若一元二次方程(b,c为常数)的两根满足,则符合条件的一个方程为_____.
7.试写出一个二次函数关系式,使它对应的一元二次方程的一个根为0,另一个根在1到2之间:________.
8.如图,在平面直角坐标系中,抛物线(m为常数,且)与直线y=2交于A、B两点.若AB=2,则m的值为______.
三、解答题
9.(1)若将y=x2﹣x﹣图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
(2)根据图象,写出当y>0时,x的取值范围.
10.已知二次函数表达式为y=x2-4x+1.
(1)求出这个二次函数图象的对称轴;
(2)求出这个二次函数的图象与坐标轴的交点坐标.
11.设二次函数(a,b是常数,),部分对应值如下表:
… …
… …
(1)试判断该函数图象的开口方向;
(2)当时,求函数y的值;
(3)根据你的解题经验,直接写出的解.
参考答案:
1.B
2.D
3.A
4.B
5.D
6.(答案不唯一)
7.
8.
9.(1)y=x2+x﹣ ;(2)x<﹣1或x>3
10.(1)直线x=2
(2)与x轴的交点坐标为(2+,0)和(2-,0),与y轴的交点坐标为(0,1)
11.(1)抛物线开口向上
(2)
(3)
5 / 6
同课章节目录
