人教版八年级上册14.1.1 同底数幂的乘法 课件 (共16张PPT)
文档属性
| 名称 | 人教版八年级上册14.1.1 同底数幂的乘法 课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 11:57:31 | ||
图片预览




文档简介
(共16张PPT)
14.1.1 同底数幂的乘法
问题:一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103秒可进行多少次运算?
如何解决这个问题呢?
1015×103
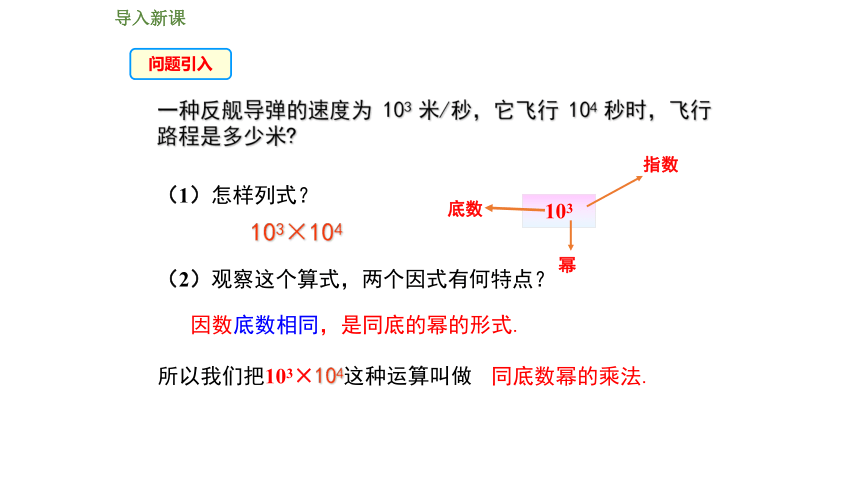
导入新课
问题引入
(1)怎样列式?
(2)观察这个算式,两个因式有何特点?
因数底数相同,是同底的幂的形式.
所以我们把103×104这种运算叫做
同底数幂的乘法.
一种反舰导弹的速度为 103 米/秒,它飞行 104 秒时,飞行路程是多少米
103×104
103
底数
指数
幂
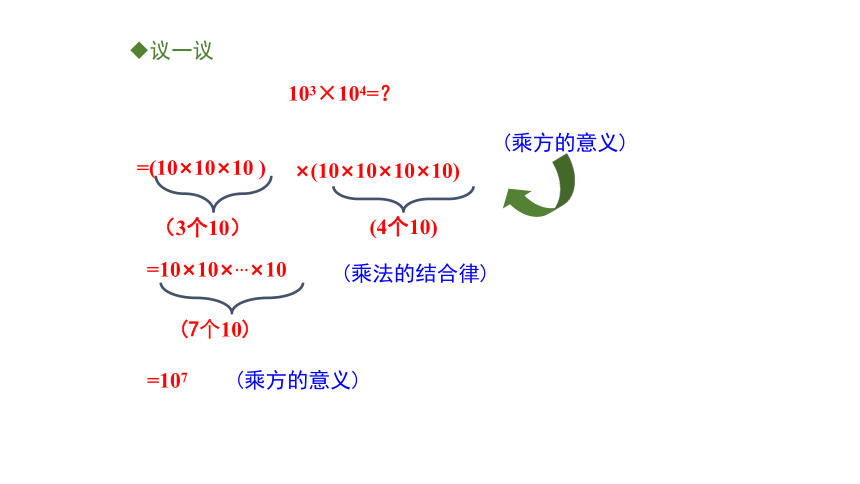
103×104=?
=(10×10×10 )
(3个10)
×(10×10×10×10)
(4个10)
=10×10×…×10
(7个10)
=107
(乘方的意义)
(乘法的结合律)
(乘方的意义)
议一议
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
探究
(2)a3·a2=a( )
7
5
(3)5m× 5n =5( )
注意观察:计算前后,底数和指数有何变化
m +n
am·an
=(aa·…a)
( 个a)
·(aa·…a)
( 个a)
=(aa·…a)
( 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+ n
m+n
证一证
猜一猜
am · an =a( ) (当m、n都是正整数)
m+n
am · an = am+n (当m、n都是正整数).
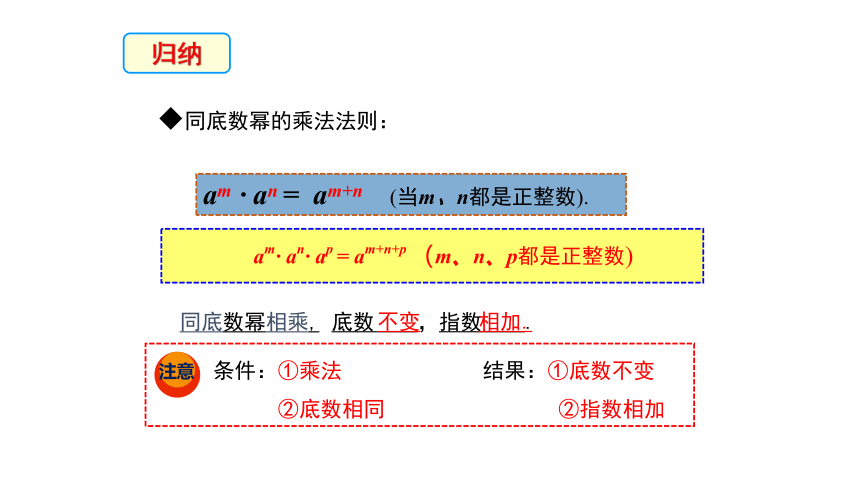
同底数幂相乘,
底数 ,指数 .
不变
相加.
同底数幂的乘法法则:
归纳
结果:①底数不变
②指数相加
注意
条件:①乘法
②底数相同
am· an· ap = am+n+p (m、n、p都是正整数)
课堂练习难点巩固小试牛刀(口答)下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
×
×
×
×
×
×
了不起!
火眼金睛
例1 计算:
(2) -a · a6 ;
= (-2) 1+2
( a 1+6 )
xm+3m+1
(1) x2 · x5 ;
(4) xm · x3m+1 ;
x2+5
= x7
(3) (-2)×(-2)2
= (-2) 3
(2) -a · a6 =-
= -a7
(3) (-2)× (-2)2;
(4) xm · x3m+1 =
= x4m+1
解 : (1) x2 · x5 =
巩固法则
负数的奇次幂是负数,负数的偶次幂是正数
温馨提示:
同底数幂相乘时,指数是相加的;
底数为负数时,先用同底数幂的乘法法则计算,最后确定结果的正负;并且化简到底
不能疏忽指数为1的情况;
公式中的a可为一个有理数、单项式或多项式(整体思想)
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
我学到 了什么?
数学方法
从特殊到一般,再从一般到特殊的思想方法,探索归纳,化归与转化等思想方法
不变,
相加.
回头一看,我想说…
学 而 不 思 则 罔
数学知识
课堂寄语:
“幂”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的.
1. a2 a3等于( )
A 3a2 B a5 C a6 D a8
2. 计算(﹣x2) (-x)3 的结果是( )
A x5 B﹣x5 C x6 D﹣x6
3.(a-b)(a-b)3(a-b)2等于( )
A.(a-b)5 B.a5-b5 C.(a-b)6 D.a6-b6
4.式子a2m+3不能写成( )
A.a2m·a3 B.am·am+3
C.a2m+3 D.am+1·am+2
100×10n-1×10n = .
6. 已知am=3,an=5,则am+n=____
过关检测
7计算:
(1)a·a3 (2)b4b4 (3)x5+x5 (4)-a3a5 (5)-a3(-a)4(-a)5 (6)(b+2)3(b+2)5(b+2) (7)(x-2y)2(2y-x)3 (8)27×3n×3 n-1
思考: 已知2x=3,2y=6,2z=36,试写出x,y,z的关系式
“数学是人类最高的智力成就,也是人类心灵最独特的创作。音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切”。
------------ 克莱因
谢谢大家!
14.1.1 同底数幂的乘法
问题:一种电子计算机每秒可进行1千万亿(1015)次运算,它工作103秒可进行多少次运算?
如何解决这个问题呢?
1015×103
导入新课
问题引入
(1)怎样列式?
(2)观察这个算式,两个因式有何特点?
因数底数相同,是同底的幂的形式.
所以我们把103×104这种运算叫做
同底数幂的乘法.
一种反舰导弹的速度为 103 米/秒,它飞行 104 秒时,飞行路程是多少米
103×104
103
底数
指数
幂
103×104=?
=(10×10×10 )
(3个10)
×(10×10×10×10)
(4个10)
=10×10×…×10
(7个10)
=107
(乘方的意义)
(乘法的结合律)
(乘方的意义)
议一议
(1)25×22=2 ( )
根据乘方的意义填空,观察计算结果,你能发现什么规律?
探究
(2)a3·a2=a( )
7
5
(3)5m× 5n =5( )
注意观察:计算前后,底数和指数有何变化
m +n
am·an
=(aa·…a)
( 个a)
·(aa·…a)
( 个a)
=(aa·…a)
( 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+ n
m+n
证一证
猜一猜
am · an =a( ) (当m、n都是正整数)
m+n
am · an = am+n (当m、n都是正整数).
同底数幂相乘,
底数 ,指数 .
不变
相加.
同底数幂的乘法法则:
归纳
结果:①底数不变
②指数相加
注意
条件:①乘法
②底数相同
am· an· ap = am+n+p (m、n、p都是正整数)
课堂练习难点巩固小试牛刀(口答)下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)y5 · y5 = 2y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
×
×
×
×
×
×
了不起!
火眼金睛
例1 计算:
(2) -a · a6 ;
= (-2) 1+2
( a 1+6 )
xm+3m+1
(1) x2 · x5 ;
(4) xm · x3m+1 ;
x2+5
= x7
(3) (-2)×(-2)2
= (-2) 3
(2) -a · a6 =-
= -a7
(3) (-2)× (-2)2;
(4) xm · x3m+1 =
= x4m+1
解 : (1) x2 · x5 =
巩固法则
负数的奇次幂是负数,负数的偶次幂是正数
温馨提示:
同底数幂相乘时,指数是相加的;
底数为负数时,先用同底数幂的乘法法则计算,最后确定结果的正负;并且化简到底
不能疏忽指数为1的情况;
公式中的a可为一个有理数、单项式或多项式(整体思想)
同底数幂相乘,
底数 指数
am · an = am+n (m、n正整数)
我学到 了什么?
数学方法
从特殊到一般,再从一般到特殊的思想方法,探索归纳,化归与转化等思想方法
不变,
相加.
回头一看,我想说…
学 而 不 思 则 罔
数学知识
课堂寄语:
“幂”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的.
1. a2 a3等于( )
A 3a2 B a5 C a6 D a8
2. 计算(﹣x2) (-x)3 的结果是( )
A x5 B﹣x5 C x6 D﹣x6
3.(a-b)(a-b)3(a-b)2等于( )
A.(a-b)5 B.a5-b5 C.(a-b)6 D.a6-b6
4.式子a2m+3不能写成( )
A.a2m·a3 B.am·am+3
C.a2m+3 D.am+1·am+2
100×10n-1×10n = .
6. 已知am=3,an=5,则am+n=____
过关检测
7计算:
(1)a·a3 (2)b4b4 (3)x5+x5 (4)-a3a5 (5)-a3(-a)4(-a)5 (6)(b+2)3(b+2)5(b+2) (7)(x-2y)2(2y-x)3 (8)27×3n×3 n-1
思考: 已知2x=3,2y=6,2z=36,试写出x,y,z的关系式
“数学是人类最高的智力成就,也是人类心灵最独特的创作。音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切”。
------------ 克莱因
谢谢大家!
