人教版九年级上册21.2.2 公式法 课件(共15张PPT)
文档属性
| 名称 | 人教版九年级上册21.2.2 公式法 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 12:37:47 | ||
图片预览






文档简介
(共15张PPT)
21.2.2 公式法
配方法
回顾与复习
1
用配方法解一元二次方程的步骤:
1.化:把二次项系数化为1(方程两边都除以二次项系数);
2.移:把常数项改变符号移到方程的另一边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.成式:方程左边一定是完全平方式
5.开方:如果右边是非负常数,就可以直接平方化一个一元二次方程为两个一元一次方程
6.求解:解这两个一元一次方程;
公式法将从这里诞生
你能用配方法解方程 2x2-9x+8=0 吗
心动 不如行动
1.化:把二次项系数化为1;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.成式 左边是完全平方式
5.开方:根据平方根意义,方程两边开平方;
6.得解:解一元一次方程;
2.移:把常数项改变符号移到方程的右边;
一元二次方程的一般形式是什么?
公式法是这样生产的
你能用配方法解方程 ax2+bx+c=0(a≠0) 吗
心动 不如行动
1.化
3.配方
4.成式
5.开方
6.求解
2.移
为什么?
公式法
一般地,对于一元二次方程 ax2+bx+c=0(a≠0)
心动 不如行动
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法
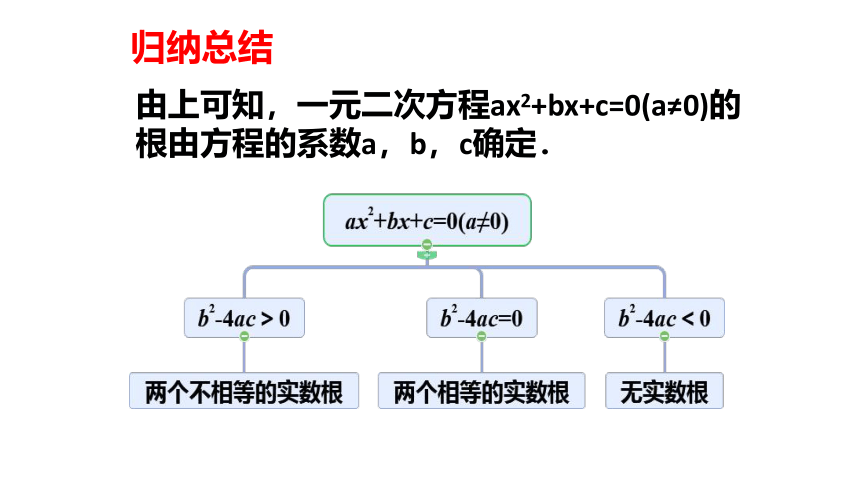
由上可知,一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a,b,c确定.
归纳总结
因此,解一元二次方程时,可以先将方程化为一般形式ax2+bx+c =0 ,当b2-4ac ≥0时,将a,b,c 代入式子
归纳总结
就得到方程的根,这个式子叫做一元二次方程的求根公式,利用它解一元二次方程的方法叫做公式法.
(2)当 b2-4ac=0 时,有两个相等的实数根。
(1)当 b2-4ac>0 时,有两个不等的实数根。
(3)当 b2-4ac<0 时,没有实数根。
一元二次方程 的根的情况
推导求根公式
不解方程判别下列方程的根的情况1、x2-6x+1=0同步练习2、2x2-x=-23、-9x2=12x+41、x2-6x+1=0解:a=1,b=-6,c=1b2-4ac=(-6)2-4×1×1=32>0所以:方程有两个不相等的实数根不解方程判别下列方程的根的情况同步练习2、2x2-x=-2解:化为一般形式2x2-x+2=0a=2,b=-1,c=2b2-4ac=(-1)2-4×2×2=-15<0所以:方程没有实数根不解方程判别下列方程的根的情况同步练习3、-9x2=12x+4解:化为一般形式9x2+12x+4=0a=9,b=12,c=4b2-4ac=122-4×9×40=0所以:方程有两个相等的实数根不解方程判别下列方程的根的情况同步练习
解: a=1、b=-4、c=-7
例题讲解
∴方程有两个不相等的实数根:
例 用公式法解方程: x 2 - 4x - 7 = 0;
(2)当 b2-4ac=0时,有两个相等的实数根。
(1)当 b2-4ac>0时,有两个不等的实数根。
(3)当 b2-4ac<0 时,没有实数根。
一元二次方程 的根的情况
小 结
21.2.2 公式法
配方法
回顾与复习
1
用配方法解一元二次方程的步骤:
1.化:把二次项系数化为1(方程两边都除以二次项系数);
2.移:把常数项改变符号移到方程的另一边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.成式:方程左边一定是完全平方式
5.开方:如果右边是非负常数,就可以直接平方化一个一元二次方程为两个一元一次方程
6.求解:解这两个一元一次方程;
公式法将从这里诞生
你能用配方法解方程 2x2-9x+8=0 吗
心动 不如行动
1.化:把二次项系数化为1;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.成式 左边是完全平方式
5.开方:根据平方根意义,方程两边开平方;
6.得解:解一元一次方程;
2.移:把常数项改变符号移到方程的右边;
一元二次方程的一般形式是什么?
公式法是这样生产的
你能用配方法解方程 ax2+bx+c=0(a≠0) 吗
心动 不如行动
1.化
3.配方
4.成式
5.开方
6.求解
2.移
为什么?
公式法
一般地,对于一元二次方程 ax2+bx+c=0(a≠0)
心动 不如行动
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法
由上可知,一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a,b,c确定.
归纳总结
因此,解一元二次方程时,可以先将方程化为一般形式ax2+bx+c =0 ,当b2-4ac ≥0时,将a,b,c 代入式子
归纳总结
就得到方程的根,这个式子叫做一元二次方程的求根公式,利用它解一元二次方程的方法叫做公式法.
(2)当 b2-4ac=0 时,有两个相等的实数根。
(1)当 b2-4ac>0 时,有两个不等的实数根。
(3)当 b2-4ac<0 时,没有实数根。
一元二次方程 的根的情况
推导求根公式
不解方程判别下列方程的根的情况1、x2-6x+1=0同步练习2、2x2-x=-23、-9x2=12x+41、x2-6x+1=0解:a=1,b=-6,c=1b2-4ac=(-6)2-4×1×1=32>0所以:方程有两个不相等的实数根不解方程判别下列方程的根的情况同步练习2、2x2-x=-2解:化为一般形式2x2-x+2=0a=2,b=-1,c=2b2-4ac=(-1)2-4×2×2=-15<0所以:方程没有实数根不解方程判别下列方程的根的情况同步练习3、-9x2=12x+4解:化为一般形式9x2+12x+4=0a=9,b=12,c=4b2-4ac=122-4×9×40=0所以:方程有两个相等的实数根不解方程判别下列方程的根的情况同步练习
解: a=1、b=-4、c=-7
例题讲解
∴方程有两个不相等的实数根:
例 用公式法解方程: x 2 - 4x - 7 = 0;
(2)当 b2-4ac=0时,有两个相等的实数根。
(1)当 b2-4ac>0时,有两个不等的实数根。
(3)当 b2-4ac<0 时,没有实数根。
一元二次方程 的根的情况
小 结
同课章节目录
