2022-2023学年人教版数学九年级上册:22.3 实际问题与二次函数 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册:22.3 实际问题与二次函数 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 20:01:21 | ||
图片预览






文档简介
(共16张PPT)
22.3 实际问题与二次函数
用二次函数解决拱桥类问题
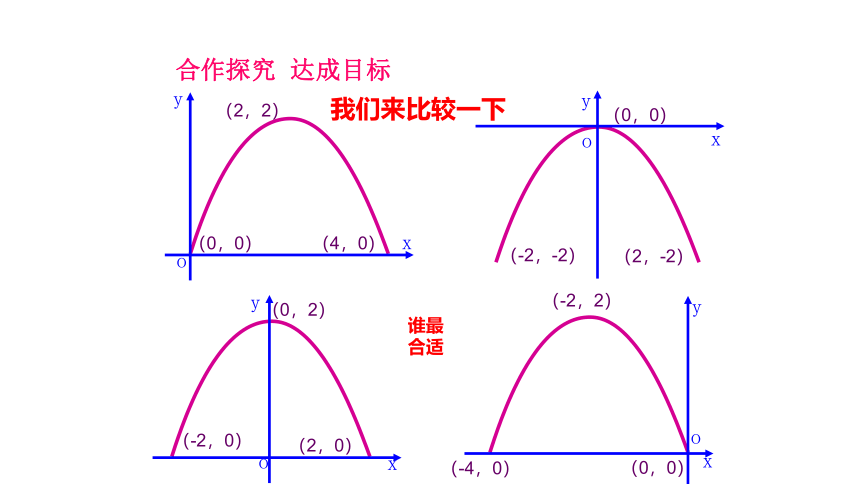
图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最合适
y
y
y
y
o
o
o
o
x
x
x
x
合作探究 达成目标
解法一: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的
二次函数的解析式为:
此时,抛物线的顶点为(0,2)
合作探究 达成目标
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
∵抛物线过点(0,0)
∴这条抛物线所表示的二次函数为:
此时,抛物线的顶点为(2,2)
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
∴这时水面的宽度为:
合作探究 达成目标
如何获得最大利润问题
利润=售价-进价
总利润=每件利润×销售数量
在日常生活中存在着许许多多的与数学知识有关的实际问题。如繁华的商业城中很多人在买卖东西。
如果你去买商品,你会选买哪一家呢?如果你是商场经理,如何定价才能使商场获得最大利润呢?
问题1.已知某商品的进价为每件40元,售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格 ,每涨价1元,每星期要少卖出10件。要想获得6090元的利润,该商品应定价为多少元?
6000
(20+x)
(300-10x)
(20+x)( 300-10x)
(20+x)( 300-10x) =6090
分析:没调价之前商场一周的利润为 元;
设销售单价上调了x元,那么每件商品的利润
可表示为 元,每周的销售量可表示为
件,一周的利润可表示为
元,要想获得6090元利润可列方程 。
自主探究
问题2.已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格 ,每涨价一元,每星期要少卖出10件。该商品应定价为多少元时,商场能获得最大利润?
解:设每件涨价为x元时获得的总利润为y元.
由题意得y =(60-40+x)(300-10x)
整理得y =-10x2+100x+6000
当x=5时,y的最大值是6250.
此时定价:60+5=65(元)
(0≤x≤30)
答:商品定价为65元时商场能获得最大利润。
问题3.已知某商品的进价为每件40元。现在
的售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格 ,每降价一元,每星期可多卖出20件。如何定价才能使利润最大?
解:设每件降价x元时的总利润为y元.
由题意得y=(60-40-x)(300+20x)
整理得 y=-20x2+100x+6000 (0≤x≤20)
当x=2.5时,y有最大值且最大值是6125.
所以定价为60-2.5=57.5时利润最大,最大值为6125元.
答:每件定价57.5元时利润最大。
问题4.已知某商品的进价为每件40元。现在
的售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格 ,每涨价一元,
每星期要少卖出10件;每降价一元,每星期
可多卖出20件。如何定价才能使利润最大?
答:综合以上两种情况,定价为65元时可
获得最大利润为6250元.
由(2)(3)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
归纳小结:
运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :
求出函数解析式和自变量的取值范围
配方变形,或利用公式求它的最大值或最小值。
检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
解这类题目的一般步骤
22.3 实际问题与二次函数
用二次函数解决拱桥类问题
图中是抛物线形拱桥,当水面在 时,拱顶离水面2m,水面宽4m,水面下降1m时,水面宽度增加了多少?
我们来比较一下
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
谁最合适
y
y
y
y
o
o
o
o
x
x
x
x
合作探究 达成目标
解法一: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-3,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的
二次函数的解析式为:
此时,抛物线的顶点为(0,2)
合作探究 达成目标
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
合作探究 达成目标
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为:
∵抛物线过点(0,0)
∴这条抛物线所表示的二次函数为:
此时,抛物线的顶点为(2,2)
合作探究 达成目标
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴当水面下降1m时,水面宽度增加了
∴这时水面的宽度为:
合作探究 达成目标
如何获得最大利润问题
利润=售价-进价
总利润=每件利润×销售数量
在日常生活中存在着许许多多的与数学知识有关的实际问题。如繁华的商业城中很多人在买卖东西。
如果你去买商品,你会选买哪一家呢?如果你是商场经理,如何定价才能使商场获得最大利润呢?
问题1.已知某商品的进价为每件40元,售价是每件 60元,每星期可卖出300件。市场调查反映:如果调整价格 ,每涨价1元,每星期要少卖出10件。要想获得6090元的利润,该商品应定价为多少元?
6000
(20+x)
(300-10x)
(20+x)( 300-10x)
(20+x)( 300-10x) =6090
分析:没调价之前商场一周的利润为 元;
设销售单价上调了x元,那么每件商品的利润
可表示为 元,每周的销售量可表示为
件,一周的利润可表示为
元,要想获得6090元利润可列方程 。
自主探究
问题2.已知某商品的进价为每件40元,售价是每件60元,每星期可卖出300件。市场调查反映:如调整价格 ,每涨价一元,每星期要少卖出10件。该商品应定价为多少元时,商场能获得最大利润?
解:设每件涨价为x元时获得的总利润为y元.
由题意得y =(60-40+x)(300-10x)
整理得y =-10x2+100x+6000
当x=5时,y的最大值是6250.
此时定价:60+5=65(元)
(0≤x≤30)
答:商品定价为65元时商场能获得最大利润。
问题3.已知某商品的进价为每件40元。现在
的售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格 ,每降价一元,每星期可多卖出20件。如何定价才能使利润最大?
解:设每件降价x元时的总利润为y元.
由题意得y=(60-40-x)(300+20x)
整理得 y=-20x2+100x+6000 (0≤x≤20)
当x=2.5时,y有最大值且最大值是6125.
所以定价为60-2.5=57.5时利润最大,最大值为6125元.
答:每件定价57.5元时利润最大。
问题4.已知某商品的进价为每件40元。现在
的售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格 ,每涨价一元,
每星期要少卖出10件;每降价一元,每星期
可多卖出20件。如何定价才能使利润最大?
答:综合以上两种情况,定价为65元时可
获得最大利润为6250元.
由(2)(3)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
归纳小结:
运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :
求出函数解析式和自变量的取值范围
配方变形,或利用公式求它的最大值或最小值。
检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
解这类题目的一般步骤
同课章节目录
