2021-2022学年江苏省各地苏科版九年级数学上册3.4方差期末试题分类选编(Word版含答案)
文档属性
| 名称 | 2021-2022学年江苏省各地苏科版九年级数学上册3.4方差期末试题分类选编(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 755.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览




文档简介
3.4 方差
1.(2022·江苏扬州·九年级期末)某商场试销一种新款衬衫,一周内销售情况如下表所示:
型号(厘米) 38 39 40 41 42 43
数量(件) 28 30 36 55 28 10
商场经理想了解哪种型号最畅销,下列关于型号的统计量中,对商场经理来说最有意义的是( )
A.平均数 B.众数 C.中位数 D.方差
2.(2022·江苏无锡·九年级期末)一组样本数据为1、2、3、3、6,下列说法错误的是( )
A.平均数是3 B.中位数是3 C.方差是3 D.众数是3
3.(2022·江苏常州·九年级期末)数据1,2,3,4,5的方差是( )
A. B.2 C.3 D.5
4.(2022·江苏南京·九年级期末)某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如表:
操作组 管理组 研发组
日工资(元/人) 260 280 300
人数(人) 4 4 4
现从管理组抽调2人,其中1人到研发组,另1人到操作组,调整后与调整前相比,下列说法不正确的是( )
A.团队日工资的平均数不变
B.团队日工资的方差不变
C.团队日工资的中位数不变
D.团队日工资的极差不变
5.(2022·江苏南京·九年级期末)一组数据1,2,,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
6.(2022·江苏宿迁·九年级期末)某同学对数据,,,,,进行统计分析发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数 B.中位数 C.方差 D.众数
7.(2022·江苏·沭阳县怀文中学九年级期末)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
8.(2022·江苏盐城·九年级期末)明明在对一组数据:10,1■,23,25,25,36,进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.众数 B.中位数 C.平均数 D.方差
9.(2022·江苏淮安·九年级期末)数据-1,0,1的方差为_______.
10.(2022·江苏宿迁·九年级期末)在一次射击比赛中,甲、乙两名运动员 10 次射击的平均成绩都是 7 环,其中甲的成绩的方差为 1.2,乙的成绩的方差为 3.9,由此可知_____的成绩更稳定.
11.(2022·江苏盐城·九年级期末)甲、乙两人在相同条件下进行射击练习,每人10次射击战绩的平均数都是8环,方差分别为,则两人射击成绩比较稳定的是________(填“甲”或“乙”).
12.(2022·江苏·射阳县第六中学九年级期末)甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.17s2,乙的方差是0.05s2,则这5次短跑训练成绩较稳定的是_____.(填“甲”或“乙”)
13.(2022·江苏徐州·九年级期末)抽查甲、乙两种消毒用品的净含量,若其方差分别为 S甲2,S乙2则净含量较为稳定的是 __.(填“甲”或“乙”)
14.(2022·江苏镇江·九年级期末)甲、乙两人在相同情况下各打靶8次,每次打靶的成绩如图所示,______(填“甲”或“乙”)的成绩更稳定.
15.(2022·江苏宿迁·九年级期末)甲、乙、丙、丁四人参加射击比赛,经过三轮的初赛,他们成绩的方差分别是,你认为成绩更稳定的是__________.
16.(2022·江苏镇江·九年级期末)一组数据21,22,23,24,25,用符号A表示,记为,加入一个数据a后,用符号B表示,记为.
①若,则A的平均数大于B的平均数;
②若,则A的方差等于B的方差;
③若,则A的中位数小于B的中位数.
其中正确的序号是______.
17.(2022·江苏扬州·九年级期末)已知一组数据1,2,3,.它们的平均数是2,则这一组数据的方差为________.
18.(2022·江苏·南京市金陵汇文学校九年级期末)有3个样本如图所示,关于它们的离散程度有下列几种说法:①样本1与样本3的离散程度相同;②样本2的离散程度最小;③三组数据的离散程度从小到大依次为:样本2、样本3、样本1.正确的序号为______.
19.(2022·江苏淮安·九年级期末)甲,乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为:9,8,9,6,10,6.甲,乙两人平均成绩相等,乙成绩的方差为4,那么成绩较为稳定的是______.(填“甲”或“乙”)
20.(2022·江苏·泰州中学附属初中九年级期末)有甲 乙两组数据,如表所示:
甲 11 12 13 14 15
乙 12 12 13 14 14
甲 乙两组数据的方差分别为,则______________(填“>”,“<”或“=”).
21.(2022·江苏江苏·九年级期末)计算一组数据的方差时,小明列了一个算式:则这组数据的平均数是________.
22.(2022·江苏泰州·九年级期末)已知1,2,3,4,5的方差为2,则2021,2022,2023,2024,2025的方差为______.
23.(2022·江苏盐城·九年级期末)疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,七、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)根据所给信息填空:
平均数(分) 中位数(分) 众数(分) 方差
七年级 85 ____________ 85 ____________
八年级 ____________ 80 ____________ 160
(2)八年级说他们的最高分人数高于七年级,所以他们的决赛成绩更好,但是七年级说他们的成绩更好,请你说出2条支持七年级的理由.
24.(2022·江苏镇江·九年级期末)为庆祝中国共产党建党100周年,某中学组织七、八年级全体学生开展了“党史知识”竞赛活动,为了解竞赛情况,从两个年级各抽取10名学生的成绩(满分为100分).
收集数据:
七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
分析数据:
平均数 中位数 众数 方差
七年级 89 m 90 39
八年级 n 90 p q
根据以上信息回答下列问题:
(1)请直接写出表格中m,n,p的值;
(2)通过计算求出q的值;
(3)通过数据分析,你认为哪个年级的成绩比较好?说明理由.
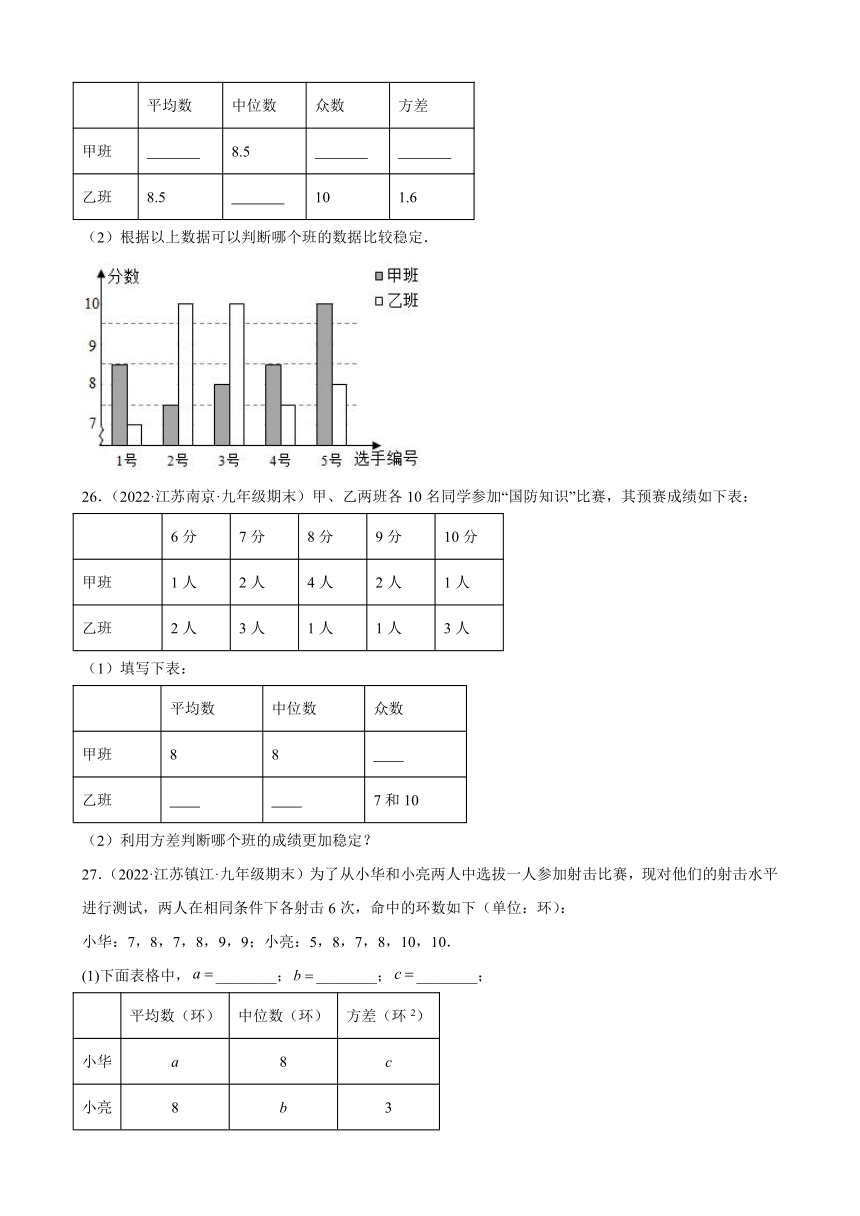
25.(2022·江苏淮安·九年级期末)某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据如图填写下表:
平均数 中位数 众数 方差
甲班 8.5
乙班 8.5 10 1.6
(2)根据以上数据可以判断哪个班的数据比较稳定.
26.(2022·江苏南京·九年级期末)甲、乙两班各10名同学参加“国防知识”比赛,其预赛成绩如下表:
6分 7分 8分 9分 10分
甲班 1人 2人 4人 2人 1人
乙班 2人 3人 1人 1人 3人
(1)填写下表:
平均数 中位数 众数
甲班 8 8
乙班 7和10
(2)利用方差判断哪个班的成绩更加稳定?
27.(2022·江苏镇江·九年级期末)为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9;小亮:5,8,7,8,10,10.
(1)下面表格中,________;________;________;
平均数(环) 中位数(环) 方差(环2)
小华 a 8 c
小亮 8 b 3
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,都命中8环,则小亮这8次射击成绩的方差________.(填“变大”、“变小”、“不变”)
28.(2022·江苏宿迁·九年级期末)为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:6,7,7,9,9,10;
小亮:5,8,7,8,10,10.
平均数(环) 中位数(环) 方差(环2)
小华 8 2
小亮 8 3
(1)表格中, ; ;
(2)根据以上表格中的信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,求小亮这8次射击成绩的方差.
29.(2022·江苏南京·九年级期末)某校为组织学生参加南京市初中学生演讲比赛,从九年级两个班各挑选5名同学先进行校内选拔,其中九(1)班5名同学的比赛成绩如下(单位:分):8,10,8,9,5.根据以上信息,解答下列问题:
(1)九(1)班5名同学比赛成绩的众数是 分,中位数是 分;
(2)求九(1)班5名同学比赛成绩的方差;
(3)九(2)班5名同学比赛成绩的平均数为8.1分,中位数为8.5分,众数为9分,方差为1.8.请你从两个不同的角度进行分析,评价哪个班挑选的5名同学在比赛中的表现更加优秀?
30.(2022·江苏盐城·九年级期末)某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试,每组20人,根据测试成绩绘制出统计表和如图所示的统计图(成绩均为整数,满分为10分)
甲组成绩统计表:
成绩 7 8 9 10
人数 1 9 5 5
根据上面的信息,解答下列问题:
(1)甲组的平均成绩为______分,甲组成绩的中位数是______,
乙组成绩统计图中______,乙组成绩的众数是______;
(2)根据图表信息,请你判断哪个小组的成绩更加稳定?只需要直接写出结论.
31.(2022·江苏泰州·九年级期末)甲、乙两名射击运动员在相同的条件下各打靶10次,每次命中的环数如下:
甲:9,7,8,9,7,6,10,10,6,8;
乙:7,8,8,9,7,8,9,8,.10,6.
(1)甲、乙两名运动员打靶的平均成绩分别是多少
(2)哪名运动员的成绩更为稳定 为什么
32.(2022·江苏泰州·九年级期末)某学校开展防疫知识线上竞赛活动,九年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)九(1)班竞赛成绩的众数是 ,九(2)班竞赛成绩的中位数是 ;
(2)哪个班的成绩较为整齐,试说明理由.
33.(2022·江苏扬州·九年级期末)某校举办了国学知识竞赛,满分100分,学生得分均为整数.在初赛中,甲乙两组学生成绩如下(单位:分):
甲组:30,60,60,60,60,60,70,90,90,100.
乙组:50,60,60,60,70,70,70,70,80,90.
组别 平均数 中位数 方差
甲组 68 376
乙组 70 116
(1)以上成绩统计分析表中 , ;
(2)小明同学说:“这次竞赛我得了70分,在我们小组中属中游偏上!”观察上面表格判断,小明可能是 组的学生;
(3)如果你是该校国学竞赛的辅导员,你会选择哪一组同学代表学校参加复赛?并说明理由.
34.(2022·江苏镇江·九年级期末)甲、乙两校各有5名学生参加区教育局举办的青少年党史知识竞赛,成绩如下表:
甲校选手得分 97 91 80 91 81
乙校选手得分 76 92 94 86 92
(1)对甲、乙两校参赛学生的成绩进行评价;
(2)如果各校从他们参赛的5名学生中派出前3名参加下一轮的决赛,你认为哪个学校的选手实力更强一些?说说你的理由.
35.(2022·江苏泰州·九年级期末)江苏省第二十届运动会将在泰州召开,某射击队准备从甲、乙二人中选拔1人参加比赛,现将两人在选拔赛中,各射击5次的成绩(单位:环数)绘制成如图所示的折线统计图.(图中只标注了部分射击数据)
观察统计图,回答下列问题:
(1)甲5次射击成绩的中位数为______环;乙5次射击成绩的平均数为______环;
(2)设甲、乙两人5次射击成绩的方差分别为,则______ ;(填“>”、“=”或“<”)
(3)如果你是教练员,你将选择谁去参加省运会?
36.(2022·江苏南京·九年级期末)甲、乙两人在相同的情况下各打靶10次,打靶成绩(单位:环)如下图所示:
(1)填表:
平均数(环) 中位数(环) 方差(环2) 命中9环及9环以上的次数
甲 ▲ 7 1.2 ▲
乙 7 7.5 ▲ 3
(2)从两个不同的角度评价甲、乙两人打靶的成绩.
37.(2022·江苏扬州·九年级期末)八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
38.(2022·江苏扬州·九年级期末)某中学九年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 2号 3号 4号 5号 总数
甲班 100 98 110 89 103 500
乙班 90 97 101 113 99 500
经统计发现两班5名学生踢毽子的总个数相等,此时有学生建议,可以通过考查数据中的其他信息为参考,请你回答下列问题:
(1)甲班比赛数据的中位数为 ,乙班比赛数据的平均数为 ;
(2)计算两班比赛数据的方差;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
39.(2022·江苏扬州·九年级期末)某中学九年级学生共进行了五次体育模拟测试,已知甲、乙两位同学五次模拟测试成绩的均分相同,小明根据甲同学的五次测试成绩绘制了尚不完整的统计表,并给出了乙同学五次测试成绩的方差的计算过程.
甲同学五次体育模拟测试成绩统计表:
次数 第一次 第二次 第三次 第四次 第五次
成绩(分) 25 29 27 a 30
小明将乙同学五次模拟测试成绩直接代入方差公式,计算过程如下:
(分2)
根据上述信息,完成下列问题:
(1)a的值是______;
(2)根据甲、乙两位同学这五次模拟测试成绩,你认为谁的体育成绩更好?并说明理由;
(3)如果甲再测试1次,第六次模拟测试成绩为28分,与前5次相比,甲6次模拟测试成绩的方差将______.(填“变大”“变小”或“不变”)
40.(2022·江苏泰州·九年级期末)某家电销售商店1~6周销售甲、乙两种品牌彩电的数量如图所示(单位:台):
(1)填表:
平均数(台) 方差(台)
甲 ______
乙 10 ______
(2)根据表中数据及折线统计图,对该商店今后采购这两种品牌彩电的意向提出建议,并说明理由.
41.(2022·江苏扬州·九年级期末)为了了解我市两家公司员工的收入情况,某数学兴趣小组的同学对甲、乙两家公司员工月收入进行了一项抽样调查,并将两家公司10名员工月收入(单位:千元)情况进行整理得到下边两幅统计图:
根据以上信息,整理分析数据如表:
平均月收入/千元 中位数 众数 方差
甲公司 a 6.5 6 1.8
乙公司 7 b 7 c
(1)填空:______;______.
(2)求c的值;
(3)某位同学的叔叔决定从两家公司中选择一家去上班,你建议他选哪家公司?说明理由.
42.(2022·江苏连云港·九年级期末)某篮球队在一次联赛中共进行了10场比赛,已知10场比赛的平均得分为88分,且前9场比赛的得分依次为:97、91、85、91、84、86、85、82、88.
(1)求第10场比赛的得分;
(2)求这10场比赛得分的中位数,众数和方差.
43.(2022·江苏连云港·九年级期末)某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是甲班和乙班各5名学生的比赛数据(单位:个):
1号 2号 3号 4号 5号 总数
甲班 89 100 96 118 97 500
乙班 100 95 110 91 104 500
经统计发现两班总数相等.此时有学生建议,可通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)甲班的优秀率为40%,乙班的优秀率为________;甲班5名学生比赛成绩的中位数是_________个,乙班5名学生比赛成绩的中位数是100个;
(2)求两班比赛数据的方差;
(3)根据以上几条信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
44.(2022·江苏江苏·九年级期末)九(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟仰卧起坐比赛,在相同的条件下,分别对两名男生进行了七次一分钟仰卧起坐测试.并对数据进行收集、整理:
甲乙两人得分表
序号 1 2 3 4 5 6 7
甲(个分钟) 25 35 36 38 40 46 46
乙(个分钟) 30 33 37 40 40 42 44
下面给出两人测试成绩的统计图表.
甲乙两人得分统计表
平均数 中位数 众数
甲 a 38 46
乙 38 b 40
解答下列问题:
(1)a= ,b= ;
(2)从方差的角度看, 的成绩较稳定(填“甲”或“乙”);
(3)甲、乙都认为自己的成绩更好些,请直接结合统计图表中的信息分别写出他们的理由.
45.(2022·江苏南京·九年级期末)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 众数 中位数 方差
甲 8 8 0.4
乙 9 3.2
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
46.(2022·江苏盐城·九年级期末)某家电销售商店第1~6周甲、乙两种品牌冰箱的周销售量如图所示(单位:台).现将这两种品牌冰箱第1~6周的销售量绘制成如下统计图表
中位数 众数 平均数 方差
甲品牌 10 10
乙品牌 9 10
(1)根据图表信息填空:____________,___________,___________;
(2)根据计算平均数和方差及折线统计图,请你对该商店今后采购这两种品牌冰箱的意向提出建议,并说明理由.
参考答案:
1.B
【解析】商场经理要了解哪些型号最畅销,所关心的即为众数.
解:根据题意知:对商场经理来说,最有意义的是各种型号的衬衫的销售数量,即众数.
故选:B.
本题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
2.C
【解析】根据平均数、中位数、众数和方差的定义逐一求解可得.
A、平均数为,故此选项不符合题意;
B、样本数据为1、2、3、3、6,则中位数为3,故此选项不符合题意;
C、方差为,故此选项符合题意;
D、众数为3,故此选项不符合题意.
故选:C.
本题考查了众数、平均数、中位数、方差.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
3.B
【解析】先计算平均数=3,代入计算即可.
∵1,2,3,4,5,
∴=3,
∴
=2,
故选B.
本题考查了方差,熟练掌握方差的计算公式是解题的关键.
4.B
【解析】根据题意分别计算调整前后的平均数,方差,中位数,极差进而进行判断即可.
解:调整前:平均数为
方差为
中位数为第六个和第七个的平均数:
极差为
调整后:平均数为
方差为
中位数为第六个和第七个的平均数:
极差为
调整前后的平均数,方差,中位数,极差,只有方差发生变化,
故选B
本题考查了求平均数,方差,中位数,极差,掌握求平均数,方差,中位数,极差是解题的关键.
5.B
【解析】根据平均数的定义先求出a的值,再根据方差公式进行计算即可.
解:∵数据1,2,a,3的平均数是3,
∴(1+2+a+3)÷4=3,
∴a=6,
∴这组数据的方差为[(1 3)2+(2 3)2+(6 3)2+(3 3)2]=.
故选:B.
本题考查了方差,一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
6.B
【解析】利用平均数、中位数、方差和标准差的定义对各选项进行判断即可.
解:这组数据的平均数、方差和标准差都与被涂污数字有关,而这组数据的中位数为36与46的平均数,与被涂污数字无关.
故选:B.
本题考查了方差:方差描述了数据对平均数的离散程度.也考查了中位数、平均数和众数的概念.
7.B
【解析】根据平均数,方差的定义计算即可.
解:∵小亮的成绩和其他39人的平均数相同,都是90分,
∴该班40人的测试成绩的平均分为90分,方差变小,
故选:B.
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
8.AB
【解析】根据众数、平均数、方差、中位数的定义解题.
解:根据题意,这组数据出现次数最多的数是25,即众数是25,与被涂污数字无关;
将这组数据按顺序排列,位于正中间的数是,即中位数是24,与被涂污数字无关;平均数与方差的计算结果均与与被涂污数字有关,故计算结果与被涂污数字无关的是:众数、中位数,
故选:AB.
本题考查众数、平均数、方差、中位数等知识,是基础考点,难度较易,掌握相关知识是解题关键.
9.
【解析】先求出3个数的平均数,再根据方差公式计算.
解:数据-1,0,1的平均数:,
方差,
故答案为:.
本题考查方差的计算,方差,熟记方差公式是解题的关键.
10.甲
【解析】根据方差的定义,方差越小数据越稳定.
解:因为S甲2=1.2<S乙2=3.9,方差小的为甲,所以本题中成绩比较稳定的是甲.
故答案为甲;
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
11.乙
【解析】根据方差的意义即方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,数据越稳定,即可得出答案.
解:,,
,
两人射击成绩比较稳定的是乙.
故答案为:乙.
此题主要考查了方差的意义和应用,要熟练掌握,解答此题的关键是要明确:方差越大,表明这组数据偏离平均数越大,数据越不稳定;方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,数据越稳定.
12.乙
【解析】根据方差的意义求解即可.
解:∵甲的方差是0.17,乙的方差是0.05,
∴甲的方差>乙的方差,
∴这5次短跑训练成绩较稳定的是乙,
故答案为:乙.
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也差;反之,则它与其平均值的离散程度越小,稳定性越好.
13.乙
【解析】方差越大,稳定性越差,方差越小,稳定性越好.比较甲乙方差大小可知乙稳定.
解:由题意可知:
∵S乙2<S甲2,
∴净含量较为稳定的是乙,
故答案为:乙.
本题考查利用方差判断稳定性,理解方差越小代表稳定性越好是解本题的关键.
14.甲
【解析】根据成绩图可以得到甲、乙8次打靶的成绩,再根据方差公式代入样本数据计算即可.
解:甲的平均数=(10+7+7+8+8+8+9+7)÷8=8,甲的方差S甲2=[(8-10)2+3×(8-7)2+3×(8-8)2+(8-9)2]÷8=1;
乙的平均数=(10+5+5+8+9+9+8+10)÷8=8,乙的方差S乙2=[2×(8-10)2+2×(8-8)2+2×(8-9)2+2×(8-5)2]÷8=3.5;
∴S甲2<S乙2,
∴甲比乙稳定.
故答案为:甲.
本题考查了平均数和方差的概念,它反映了一组数据的波动大小,方差越大,波动性越大反之也成立.
15.甲
【解析】根据方差的定义,方差越小数据越稳定即可求解.
解:∵,
∴方差最小的为甲,
∴成绩更稳定的是甲.
故答案为:甲.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
16.①③##③①
【解析】根据方差、平均数、中位数的概念求解.
解:①若a=22,则A的平均数为=23,
B的平均数,
∴A的平均数大于B的平均数,正确;
②若a=23,则A的平均数为=23,
A的方差:×[(23-21)2+(23-22)2+(23-23)2+(23-24)2+(23-25)2]=2,
B的平均数,
B的方差:×[(23-21)2+(23-22)2+(23-23)2+(23-24)2+(23-25)2+(23-23)2]=,
∴A的方差不等于B的方差,错误;
③若a=24,则A的中位数为23,
B的中位数=23.5.
∴A的中位数小于B的中位数,正确.
故答案为:①③.
本题考查了方差、众数、平均数、中位数的知识,解答本题的关键是掌握各知识点的概念.
17.
【解析】根据平均数的性质,通过列一元一次方程并求解,即可得;再根据方差的性质计算,即可得到答案.
∵一组数据1,2,3,.它们的平均数是2,
∴
∴
∴这一组数据的方差为:
故答案为:.
本题考查了数据分析、一元一次方程的知识;解题的关键是熟练掌握平均数和方差的性质,从而完成求解.
18.②③##③②
【解析】分别计算出三个样本的平均数及方差,根据方差越小离散程度越小即可判断.
解:根据平均数,方差的计算方法,依次计算如下:
样本1的平均数,
方差,
样本2的平均数,
方差,
样本3的平均数,
方差,
,
样本2的方差最小,即样本2的离散程度最小,故②正确;
三数数据的离散程度从小到大一次为:样本2、样本3、样本1,故③正确;
样本1与样本3的离散程度不相同,故①错误;
故答案为:②③.
本题考查了方差,解题的关键是掌握求方差的基本公式及方法.
19.甲.
【解析】先计算出甲的平均数,再计算甲的方差,然后比较甲乙方差的大小可判定谁的成绩稳定.
甲的平均数,
所以甲的方差,
因为甲的方差比乙的方差小,
所以甲的成绩比较稳定.
故答案为甲.
本题考查方差的定义:一般地设n个数据,,,…,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
20.>
【解析】根据甲、乙两组数据分别求出甲、乙的平均数,然后再利用方差公式进行求解比较即可.
解:由题意得:
,,
∴,
,
∴,
∴;
故答案为>.
本题主要考查平均数及方差,熟练掌握平均数及方差的计算是解题的关键.
21.3
【解析】根据方差的计算公式即可得出答案.
解:∵,
∴这组数据的平均数是3,
故答案为:3.
本题主要考查方差,解题的关键是掌握方差的定义及其计算公式.
22.2
【解析】将第二组数据中的每一个数据均减去2020后得到一组新数据与甲数据相等,由此可以得到两组数据的方差相同.
解:将数据:2021、2022、2023、2024、2025都减去2020后得到数据1、2、3、4、5,
与数据:1、2、3、4、5的方差相同,是2
故答案为:2.
本题考查了方差,牢记方差的变化规律是解决此类问题的关键.
23.(1)85;70;85;100
(2)理由见解析
【解析】(1)从图上读取信息,由平均数、中位数、众数、方差的定义即可得到答案.
(2)对比七、八年级的相关数据,从中位数、方差的意义分析即可得到答案.
(1)
解:
平均数(分) 中位数(分) 众数(分) 方差
七年级 85 85 85 70
八年级 85 80 100 160
(2)
解:①七年级成绩的方差低于八年级,成绩比八年级稳定,
②七年级的中位数比八年级高,所以七年级成绩好一些.
本题考查平均数、中位数、众数、方差的定义及其意义,熟练掌握相关知识是解题的关键.
24.(1)m=90,n =90,p =90
(2)30
(3)八年级的学生成绩好,见解析
【解析】(1)由中位数、众数、平均数的定义求解即可得出答案;
(2)根据方差的定义列式计算即可;
(3)在七、八年级学生成绩的中位数和众数相同的前提下,根据平均数和方差的意义即可判断;
(1)
解:七年级的中位数为=90分,故m=90;
八年级的平均数为:×(85+85+95+80+95+90+90+90+100+90]=90,故n=90;
八年级中90分的最多,故p=90;
(2)
解:八年级的方差q=×[(80﹣90)2+2×(85﹣90)2+4×(90﹣90)2+2×(95﹣90)2+(100﹣90)2]=30;
(3)
解:八年级的学生成绩好,
理由如下:七、八年级学生成绩的中位数和众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更稳定,
综上,八年级的学生成绩好;
本题考查了中位数、众数、平均数、方差等统计基础知识,明确相关统计量表示的意义及相关计算方法是解题的关键.
25.(1)8.5,8,8.5,0.7;(2)甲班的成绩更稳定.
【解析】(1)根据平均数和众数的概念求出甲的平均数与众数,根据方差的计算公式求出甲的方差;
(2)根据方差的性质解答.
解:(1)甲的平均数为=8.5,众数为:8.5,
方差为:[(8.5﹣8.5)2+(7.5﹣8.5)2+(8﹣8.5)2+(8.5﹣8.5)2+(10﹣8.5)2]=0.7,
乙的中位数是8,
(2)从方差看,甲班的方差小,所以甲班的成绩更稳定.
此题主要考查统计调查的应用,解题的关键是熟知平均数、方差、众数及中位数的求解方法.
26.(1)8;8;7.5;(2)甲班的成绩更加稳定
【解析】(1)分别求出甲、乙两班的平均数、中位数、众数,即可得到答案;
(2)分别求出甲、乙两个班的方差,即可进行判断.
解:(1)甲班的众数为:8;
乙班的平均数为:;
乙班的中位数为:;
故答案为:8;8;7.5;
(2)甲班的方差为:
;
乙班的方差为:
;
∵,
∴,
∴甲班的成绩更加稳定;
本题考查了利用方差判断稳定性,也考查了加权平均数、众数、中位数,解题的关键是熟练掌握所学的知识,正确的进行数据的处理.
27.(1)8,8,.
(2)选择小华参赛,理由见解析.
(3)变小.
【解析】(1)根据平均数、中位数、方差的计算方法分别计算即可;
(2)通过平均数、方差的大小,得出结论;
(3)计算出小亮再射击2次后8次的平均数、方差,通过方差的比较得出答案.
(1)
解:小华的平均成绩(环),
小华的方差(环),
把小亮的成绩从小到大排列为5,7,8,8,10,10,
则中位数(环),
故答案为:8,8,.
(2)
解:∵小亮的方差是3,小华的方差是,即,
又∵小亮的平均数和小华的平均数相等,
∴选择小华参赛.
(3)
解:小亮再射击后的平均成绩是(环),
射击后的方差是:,
∴小亮这8次射击成绩的方差变小,
故答案为:变小.
此题考查平均数、中位数、方差的意义和计算方法,明确各个统计量的意义及反应数据的特征是正确解答的关键.
28.(1)8,8
(2)小华,理由见解析
(3)环2
【解析】(1)根据平均数、中位数的计算方法分别计算即可;
(2)通过平均数、方差的大小,得出结论;
(3)计算出小亮再射击后的平均数、方差即可得出答案.
(1)
解:小华的平均成绩为a=(6+7+7+9+9+10)÷6=8(环),
把小亮的成绩从小到大排列为5,7,8,8,10,10,
则中位数为=8(环),
故答案为:8,8;
(2)
解:选择小华参赛,理由如下:
∵小亮的方差是3,小华的方差是2,即3>2,而小亮的平均数和小华的平均数相等,
∴小华的成绩稳定,
∴选择小华参赛;
(3)
解:小亮再射击后的平均成绩是(8×6+7+9)÷8=8(环),
射击后的方差是:
×[(5-8)2+(7-8)2×2+(8-8)2×2+(10-8)2×2+(9-8)2]=2.5(环2).
此题考查平均数、中位数、方差的意义和计算方法,明确各个统计量的意义及反应数据的特征是正确解答的关键.
29.(1)8,8
(2)九(1)班5名同学比赛成绩的方差
(3)从数据的集中程度平均数来看,九(2)班五名同学在比赛中的表现更加优秀;从数据的离散程度方差来看,九(2)班五名同学在比赛中表现更加优秀
【解析】(1)将数字从左往右依次排列,出现次数最多的数字为众数,数据中居于中间位置的数叫做中位数;
(2)若的平均数为m,则方差公式可表示为: ,根据方差公式计算方差即可;
(3)答案不唯一,选择数据的某一方面的特点加以分析即可.
(1)
解:将数据由小到大排列为:5,8,8,9,10
则由数据可知众数为:8,
中位数为:8,
故答案为:8;8 .
(2)
九年级(1)班参赛选手的平均成绩=(8+10+8+9+5)÷5=8(次),
则方差S2=×(0+4+0+1+9)=.
(3)
答案不唯一
①如从数据的集中程度平均数来看,因为九(2)班平均成绩高于九(1)班,所以九(2)
班五名同学在比赛中的表现更加优秀;
②从数据的离散程度方差来看,因为九(2)班五名同学成绩的方差小于九(1)班,所以九(2)班五名同学表现更加稳定,且九(2)班平均成绩高于九(1)班,所以九(2)班五名同学在比赛中表现更加优秀.
本体考察数据的收集与整理,能熟练掌握方差的求法,并根据数据的特点对提供数据的事件进行分析是解决本体的关键.
30.(1)8.7;8.5;3;8
(2)乙组
【解析】(1)用总人数减去其他成绩的人数,求出m,再根据中位数和众数的定义即可求出甲组成绩的中位数和乙组成绩的众数;
(2)先求出平均数,再根据方差公式求出甲、乙组的方差,然后进行比较,即可得出答案.
(1)
(1)甲组的平均成绩为: = 8.7(分),
甲组成绩的中位数是= 8.5(分),
乙组成绩统计图中m= 20- (2 +9+6)= 3,
乙组成绩的众数是8分,
故答案为: 8.7, 8.5分, 3, 8分;
(2)
(2)乙组的成绩更加稳定,
甲组的方差为:
[(7-8.7)2 +9×(8-8.7)2 +5×(9- 8.7)2 +5×(10- 8.7)2]= 0.81,
乙组平均成绩是: ×(2×7+9×8+6×9+3×10)= 8.5(分),
乙组的方差为:
[2×(7-8.5)2+9×(8-8.5)2+6×(9-8.5)2+3×(10-8.5)2]=0.75,
∴<
所以乙组的成绩更稳定.
此题考查了平均数、众数和中位数,方差的有关内容,解题的关键是正确理解统计图,学会计算方差.
31.(1),
(2)乙更稳定,理由见解析
【解析】(1)根据平均数的公式:平均数=所有数之和再除以数的个数;
(2)先根据方差公式进行计算,方差越大,波动越大,成绩越不稳定,射击水平越差,反之也成立.
(1)
解:甲、乙两人射击成绩的平均成绩分别为:
;
.
(2)
,
,
∵,
∴乙更稳定.
本题考查平均数和方差的计算,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.平均数反映了一组数据的集中程度,求平均数的方法是所有数之和再除以数的个数;方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法.
32.(1)80分,85分
(2)九(1)班成绩较为整齐,理由见解析
【解析】(1)根据众数和中位数的概念求解即可;
(2)根据方差的定义和意义求解即可.
(1)
解:由图知,九(1)班成绩为80、80、80、90、100,
九(2)班成绩为70、80、85、95、100,
所以九(1)班成绩的众数为80分,九(2)班成绩的中位数为85分;
故答案为:80分,85分.
(2)
解:九(1)班成绩较为整齐,理由如下:
∵九(1)班成绩的平均数为=86(分),
九(2)班成绩的平均数为=86(分),
∴九(1)班成绩的方差为×[3×(80-86)2+(90-86)2+(100-86)2]=64,
九(2)班成绩的方差为×[(70-86)2+(80-86)2+(85-86)2+(95-86)2+(100-86)2]=114,
∴九(1)班成绩较为整齐.
本题主要考查条形统计图、众数、中位数和方差,解题的关键是掌握众数、中位数和方差的定义以及方差的意义.
33.(1)60,68
(2)甲
(3)选乙组参加复赛,理由见解析
【解析】(1)根据平均数和中位数的定义分别进行解答即可得出答案;
(2)根据中位数的意义即可得出答案;
(3)根据方差的意义即可得出答案.
(1)
解:把甲组的成绩从小到大排列为,最中间的数是=60(分),
则中位数a=60分;
b=×(50+60+60+60+70+70+70+70+80+90)=68(分),
故答案为:60,68;
(2)
解:小明可能是甲组的学生,理由如下:
因为甲组的中位数是60分,而小明得了70分,所以在小组中属中游略偏上,
故答案为:甲;
(3)
解:选乙组参加复赛.理由如下:
∵S甲2=376>S乙2=116,
∴乙组的成绩比较稳定,而且乙组的中位数大于甲组的中位数,
选乙组参加复赛.
本题考查了平均数,中位数,方差的意义.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
34.(1)甲、乙两校的平均分相等,甲校的方差小于乙校的方差,因此甲校学生的成绩较稳定,成绩较好
(2)甲校的平均分高于乙校,因此甲校的选手实力更强些
【解析】(1)计算甲、乙两校参赛学生成绩的平均分,众数,中位数,方差,再进行分析即可;
(2)计算各校前3名的平均分,比较即可.
(1)
解:由表中数据可知,甲校的平均分是=88(分),
众数是91,
中位数是91,
方差是×[(88-97)2+(88-91)2+(88-80)2+(88-91)2+(88-81)2]=42.4;
乙校的平均分是=88(分),
众数是92,
中位数是92,
方差是×[(88-76)2+(88-92)2+(88-94)2+(88-86)2+(88-92)2]=43.2.
甲、乙两校的平均分相等,甲校的方差小于乙校的方差,因此甲校学生的成绩较稳定,成绩较好;
(2)
甲校派出选手的成绩为91、91、97,平均分是,
乙校派出选手的成绩为92、92、94,平均分是,
甲校的平均分高于乙校,因此甲校的选手实力更强些.
本题考查了方差、众数、中位数以及平均数,掌握方差、众数、中位数以及平均数的定义是解题的关键.
35.(1),
(2)
(3)选择乙去参加省运会,理由见解析
【解析】(1)根据中位数、平均数的定义分别进行解答即可得出答案;
(2)根据方差的意义,结合折线统计图即可求解;
(3)根据中位数、方差的意义即可得出答案.
(1)
解:(1)把甲5次射击成绩按从小到大的顺序排列,第3个数是8.2,所以甲5次射击成绩的中位数为8.2环;
乙5次射击成绩为:,,,,,
平均数为环;
故答案为:,;
(2)
解:根据折线图可知,乙5次射击成绩与其平均值的偏离程度较小,成绩更稳定,即.
故答案为: ;
(3)
解:选择乙去参加省运会,理由如下:
因为乙的中位数是8.4环,高于甲的中位数,而且,乙的成绩比甲更稳定,
所以应选乙去参加省运会.
本题考查了折线统计图.读懂统计图,从统计图中得到必要的信息是解决问题的关键.也考查了中位数、平均数和方差的意义.
36.(1)7; 5.4; 1
(2)甲打靶的成绩更稳定,(答案不唯一)理由见解析
【解析】(1)根据图象将甲乙打靶成绩都写出来,然后依据平均数及方差的计算方法求解即可;
(2)评价方法可以从平均数或者方差方面进行分析即可.
(1)
解:由图可得甲的打靶环数分别为:9,5,7,8,7,6,8,6,7,7,
∴甲打靶的平均成绩为:
,
乙的打靶环数分别为:2,4,6,8,7,7,8,9,9,10,
∴乙打靶的方差为:
=5.4;
甲成绩中命中9环及以上的只有1次,
故答案为:7;5.4;1;
(2)
本题答案不唯一,下列解法供参考.例如:
①甲、乙打靶的成绩的平均数都是7环,说明两人的打靶实力相当;
②甲、乙两人打靶的成绩的方差分别是1.2环2和5.4环2,说明甲打靶的成绩更稳定.
题目主要考查计算数据的平均数及方差,利用平均数或方差作决策等,理解题意,熟练掌握运用平均数及方差的计算方法是解题关键.
37.(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【解析】(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
本题考查方差、中位数和众数:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
38.(1)100,100
(2),
(3)应该把团体第一名的奖状给甲班,因为甲班和乙班的平均数相同,甲班的方差比乙班低,甲班比较稳定,综合评定甲班比较好
【解析】(1)
解:甲班的成绩重新排列为:89,98,100,103,110,故中位数为100,
乙班成绩的平均数为,
故答案为:100,100;
(2)
甲的平均数为:500÷5=100(个),
S甲2=[(100﹣100)2+(98﹣100)2+(110﹣100)2+(89﹣100)2+(103﹣100)2]÷5=46.8;
乙的平均数为:500÷5=100(个),
S乙2=[(90﹣100)2+(97﹣100)2+(101﹣100)2+(113﹣100)2+(99﹣100)2]÷5=56;
(3)
应该把团体第一名的奖状给甲班,理由如下:因为甲班和乙班的平均数相同,甲班的方差比乙班低,甲班比较稳定,综合评定甲班比较好.
此题考查了统计计算,正确掌握中位数的定义,平均数的计算公式,方差的计算公式,利用方差做决策是解题的关键.
39.(1)29
(2)乙的体育成绩更好,理由见解析
(3)变小
【解析】(1)根据平均分相同,根据乙的方差公式可得乙的平均分为28,则甲的平均分也为28,进而求得的值;
(2)根据甲的成绩计算甲的方差,比较甲乙的方差,方差小的体育成绩更好;
(3)根据第六次的成绩等于平均数,根据方差公式可知方差将变小.
(1)
解:甲、乙两位同学五次模拟测试成绩的均分相同,
乙的方差为:
则平均分为28
所以甲的平均分为28
则
解得
故答案为:29
(2)
乙的成绩更好,理由如下,
乙的成绩较稳定,则乙的体育成绩更好
(3)
甲6次模拟测试成绩的方差将变小
故答案为:变小
本题考查了求方差,平均数,根据方差判断稳定性,掌握求方差的公式是解题的关键.
40.(1)10,
(2)甲品牌,理由见解析
【解析】(1)先通过折线图获得数据,后利用平均数的计算公式,方差计算公式分别计算即可;
(2)选择从平均数,方差等统计特征量的角度去分析,答案不是唯一的,只要合理即可.
(1)
∵甲的数据为:7,10,8,10,12,13,
∴=10,
∵乙的数据为:9,10,11,9,12,9,,
∴
=,
故答案为:10,.
(2)
两种品牌的彩电的周平均销售量相同,乙品牌彩电周销售量的方差较小,说明乙品牌的彩电周销售量比较稳定,从折线统计图看,甲品牌的彩电的周销售量呈上升趋势,建议商家可以多采购甲品牌的彩电(答案是开放的,言之有理即).
本题考查了折线统计图,平均数,方差,根据统计图获得信息,并熟练进行相关的计算是解题的关键.
41.(1)7,7
(2)1.4
(3)选乙公司,理由见解析
【解析】(1)利用平均数、中位数的定义分别计算后即可确定正确的答案;
(2)利用方差的计算公式进行计算后即可确定正确的答案;
(3)根据平均数一样,中位数及众数的大小和方差的大小进行选择即可.
(1)
甲公司员工月收入6千元占比为:
甲公司员工的平均月收入为:(千元)
∴
乙公司员工月收入从小至大排列为:5,5,7,7,7,7,7,8,8,9,
∴中位数为7
∴
故答案为:7,7
(2)
∵
∴
∴
(3)
选乙公司,理由如下:
因为月收入平均数一样,中位数、众数乙公司大于甲公司,且乙公司方差小,更稳定.
本题考查了求平均数、中位数、众数和方差,解题的关键是能够了解有关的计算公式.
42.(1)91;(2)中位数为87分,众数为91分和方差18.2分.
【解析】(1)根据平均数的定义求出第10场比赛的得分;
(2)再根据中位数、众数的定义、方差公式求出中位数、众数和方差.
解:(1)解:设第10场比赛得分为x,
根据题意知,(97+91+85+x+91+84+86+85+82+88)÷10=88,
解得x=91,
所以第10场比赛得分91分;
(2)在这一组数据中91是出现次数最多的,故众数是91;
将这组数据从小到大的顺序排列(82,84,85,85,86,88,91,91,91,97),处于中间位置的数是86、88,
由中位数的定义可知,这组数据的中位数是(86+88)÷2=87,
,
故这10场比赛得分的中位数为87分,众数为91分和方差18.2分.
此题考查了平均数、众数与中位数和方差.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;众数是一组数据中出现次数最多的数;一般地设n个数据,x1,x2,…xn的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
43.(1)60%;97;
(2)94;44.4
(3)冠军奖杯应发给乙班,理由见解析
【解析】(1)优秀率就是优秀的人数与总人数的百分比;
(2)根据平均数和方差的概念计算.
(3)根据计算出来的统计量的意义分析判断.
(1)
乙班的优秀率:×100%=60%;
把甲班5名同学踢的个数从小到大排列为:89,96,97,100,118,
则甲班5名学生比赛成绩的中位数是97个;
故答案为:60%;97;
(2)
甲班的平均数是:(89+100+96+118+97)÷5=100(个),
甲班的方差
乙班的平均数是:(100+95+110+91+104)÷5=100(个),
乙班的方差;
(3)
冠军奖杯应发给乙班,理由如下:
因为两班总数相等,但乙班5名学生的比赛成绩的优秀率比甲班高,中位数比甲班大,方差比甲班小,成绩更稳定,综合评定乙班踢毽子水平较好.
本题考查了中位数、平均数和方差等概念以及运用.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动.
44.(1)38,40
(2)乙
(3)见解析
【解析】(1)根据平均数的计算公式及中位数的定义解答;
(2)根据折线图直接得到答案;
(3)根据表格中的数据分析得到比较即可.
(1)
解:38,b=40,
故答案为:38,40;
(2)
解:由甲、乙两人得分的大小波动情况,直观可得,
∴乙的得分较稳定.
故答案为:乙;
(3)
甲的成绩更好些,理由为:甲得分的众数比乙的高.
乙的成绩更好些,理由为:乙得分的中位数比甲的高.(或写乙得分较稳定也可以).
此题考查了统计知识,掌握平均数的计算公式,中位数的定义,分析比较折线统计图及统计表得到相关数据,正确掌握各知识点并应用是解题的关键.
45.(1)填表见解析;(2)理由见解析;(3)变小.
【解析】(1)根据众数、平均数和中位数的定义求解:
(2)方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
(3)根据方差公式求解:如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
解:(1)根据数据可得:甲的众数为8,
乙的平均数=(5+9+7+10+9)=8,
将乙的数据重新排序为:5,7,9,9,10
乙的中位数为9;
故填表如下:
平均数 众数 中位数 方差
甲 8 8 8 0.4
乙 8 9 9 3.2
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)如果乙再射击1次,命中8环,平均数不变,
则乙的方差为,
所以乙的射击成绩的方差变小.
题目主要考查众数、平均数和中位数的求法,利用方差作决策等,理解题意,熟练掌握运用各个数据的求法是解题关键.
46.(1)9.5,10,
(2)见解析
【解析】(1)先根据图表,确定数据,后根据所求,逐一计算即可.
(2) 比较后,提出合理化的建议即可.
(1)
∵甲品牌的数据为:7,10,8.,10,12,13,
∴,
∴b=10,
∴=,
∴c=,
∵乙品牌的数据为:9,10,11.,9,12,9,
∴9,9,9,10,11., 12,
∴中位数为:=9.5,
∴a=9.5,
故答案为:9.5,10,.
(2)
甲、乙两种品牌冰箱周销售量的平均数相同,而乙品牌冰箱周销售量的方差较小,说明乙品牌冰箱周销售量比较稳定,所以可选择采购乙品牌的冰箱;从折线图来看,甲品牌冰箱的月销售量呈上升趋势,所以进货时可多进甲品牌冰箱.
本题考查了平均数,中位数,方差,熟练从图表中获取解题信息并灵活运用公式计算是解题的关键.
1.(2022·江苏扬州·九年级期末)某商场试销一种新款衬衫,一周内销售情况如下表所示:
型号(厘米) 38 39 40 41 42 43
数量(件) 28 30 36 55 28 10
商场经理想了解哪种型号最畅销,下列关于型号的统计量中,对商场经理来说最有意义的是( )
A.平均数 B.众数 C.中位数 D.方差
2.(2022·江苏无锡·九年级期末)一组样本数据为1、2、3、3、6,下列说法错误的是( )
A.平均数是3 B.中位数是3 C.方差是3 D.众数是3
3.(2022·江苏常州·九年级期末)数据1,2,3,4,5的方差是( )
A. B.2 C.3 D.5
4.(2022·江苏南京·九年级期末)某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如表:
操作组 管理组 研发组
日工资(元/人) 260 280 300
人数(人) 4 4 4
现从管理组抽调2人,其中1人到研发组,另1人到操作组,调整后与调整前相比,下列说法不正确的是( )
A.团队日工资的平均数不变
B.团队日工资的方差不变
C.团队日工资的中位数不变
D.团队日工资的极差不变
5.(2022·江苏南京·九年级期末)一组数据1,2,,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
6.(2022·江苏宿迁·九年级期末)某同学对数据,,,,,进行统计分析发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数 B.中位数 C.方差 D.众数
7.(2022·江苏·沭阳县怀文中学九年级期末)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
8.(2022·江苏盐城·九年级期末)明明在对一组数据:10,1■,23,25,25,36,进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.众数 B.中位数 C.平均数 D.方差
9.(2022·江苏淮安·九年级期末)数据-1,0,1的方差为_______.
10.(2022·江苏宿迁·九年级期末)在一次射击比赛中,甲、乙两名运动员 10 次射击的平均成绩都是 7 环,其中甲的成绩的方差为 1.2,乙的成绩的方差为 3.9,由此可知_____的成绩更稳定.
11.(2022·江苏盐城·九年级期末)甲、乙两人在相同条件下进行射击练习,每人10次射击战绩的平均数都是8环,方差分别为,则两人射击成绩比较稳定的是________(填“甲”或“乙”).
12.(2022·江苏·射阳县第六中学九年级期末)甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.17s2,乙的方差是0.05s2,则这5次短跑训练成绩较稳定的是_____.(填“甲”或“乙”)
13.(2022·江苏徐州·九年级期末)抽查甲、乙两种消毒用品的净含量,若其方差分别为 S甲2,S乙2则净含量较为稳定的是 __.(填“甲”或“乙”)
14.(2022·江苏镇江·九年级期末)甲、乙两人在相同情况下各打靶8次,每次打靶的成绩如图所示,______(填“甲”或“乙”)的成绩更稳定.
15.(2022·江苏宿迁·九年级期末)甲、乙、丙、丁四人参加射击比赛,经过三轮的初赛,他们成绩的方差分别是,你认为成绩更稳定的是__________.
16.(2022·江苏镇江·九年级期末)一组数据21,22,23,24,25,用符号A表示,记为,加入一个数据a后,用符号B表示,记为.
①若,则A的平均数大于B的平均数;
②若,则A的方差等于B的方差;
③若,则A的中位数小于B的中位数.
其中正确的序号是______.
17.(2022·江苏扬州·九年级期末)已知一组数据1,2,3,.它们的平均数是2,则这一组数据的方差为________.
18.(2022·江苏·南京市金陵汇文学校九年级期末)有3个样本如图所示,关于它们的离散程度有下列几种说法:①样本1与样本3的离散程度相同;②样本2的离散程度最小;③三组数据的离散程度从小到大依次为:样本2、样本3、样本1.正确的序号为______.
19.(2022·江苏淮安·九年级期末)甲,乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为:9,8,9,6,10,6.甲,乙两人平均成绩相等,乙成绩的方差为4,那么成绩较为稳定的是______.(填“甲”或“乙”)
20.(2022·江苏·泰州中学附属初中九年级期末)有甲 乙两组数据,如表所示:
甲 11 12 13 14 15
乙 12 12 13 14 14
甲 乙两组数据的方差分别为,则______________(填“>”,“<”或“=”).
21.(2022·江苏江苏·九年级期末)计算一组数据的方差时,小明列了一个算式:则这组数据的平均数是________.
22.(2022·江苏泰州·九年级期末)已知1,2,3,4,5的方差为2,则2021,2022,2023,2024,2025的方差为______.
23.(2022·江苏盐城·九年级期末)疫情防控人人有责,为此我校在七、八年级举行了“新冠疫情防控”知识竞赛,七、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)根据所给信息填空:
平均数(分) 中位数(分) 众数(分) 方差
七年级 85 ____________ 85 ____________
八年级 ____________ 80 ____________ 160
(2)八年级说他们的最高分人数高于七年级,所以他们的决赛成绩更好,但是七年级说他们的成绩更好,请你说出2条支持七年级的理由.
24.(2022·江苏镇江·九年级期末)为庆祝中国共产党建党100周年,某中学组织七、八年级全体学生开展了“党史知识”竞赛活动,为了解竞赛情况,从两个年级各抽取10名学生的成绩(满分为100分).
收集数据:
七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
分析数据:
平均数 中位数 众数 方差
七年级 89 m 90 39
八年级 n 90 p q
根据以上信息回答下列问题:
(1)请直接写出表格中m,n,p的值;
(2)通过计算求出q的值;
(3)通过数据分析,你认为哪个年级的成绩比较好?说明理由.
25.(2022·江苏淮安·九年级期末)某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据如图填写下表:
平均数 中位数 众数 方差
甲班 8.5
乙班 8.5 10 1.6
(2)根据以上数据可以判断哪个班的数据比较稳定.
26.(2022·江苏南京·九年级期末)甲、乙两班各10名同学参加“国防知识”比赛,其预赛成绩如下表:
6分 7分 8分 9分 10分
甲班 1人 2人 4人 2人 1人
乙班 2人 3人 1人 1人 3人
(1)填写下表:
平均数 中位数 众数
甲班 8 8
乙班 7和10
(2)利用方差判断哪个班的成绩更加稳定?
27.(2022·江苏镇江·九年级期末)为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:7,8,7,8,9,9;小亮:5,8,7,8,10,10.
(1)下面表格中,________;________;________;
平均数(环) 中位数(环) 方差(环2)
小华 a 8 c
小亮 8 b 3
(2)根据以上信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,都命中8环,则小亮这8次射击成绩的方差________.(填“变大”、“变小”、“不变”)
28.(2022·江苏宿迁·九年级期末)为了从小华和小亮两人中选拔一人参加射击比赛,现对他们的射击水平进行测试,两人在相同条件下各射击6次,命中的环数如下(单位:环):
小华:6,7,7,9,9,10;
小亮:5,8,7,8,10,10.
平均数(环) 中位数(环) 方差(环2)
小华 8 2
小亮 8 3
(1)表格中, ; ;
(2)根据以上表格中的信息,你认为教练会选择谁参加比赛,理由是什么?
(3)若小亮再射击2次,分别命中7环和9环,求小亮这8次射击成绩的方差.
29.(2022·江苏南京·九年级期末)某校为组织学生参加南京市初中学生演讲比赛,从九年级两个班各挑选5名同学先进行校内选拔,其中九(1)班5名同学的比赛成绩如下(单位:分):8,10,8,9,5.根据以上信息,解答下列问题:
(1)九(1)班5名同学比赛成绩的众数是 分,中位数是 分;
(2)求九(1)班5名同学比赛成绩的方差;
(3)九(2)班5名同学比赛成绩的平均数为8.1分,中位数为8.5分,众数为9分,方差为1.8.请你从两个不同的角度进行分析,评价哪个班挑选的5名同学在比赛中的表现更加优秀?
30.(2022·江苏盐城·九年级期末)某学校从九年级同学中任意选取40人,随机分成甲、乙两个小组进行“引体向上”体能测试,每组20人,根据测试成绩绘制出统计表和如图所示的统计图(成绩均为整数,满分为10分)
甲组成绩统计表:
成绩 7 8 9 10
人数 1 9 5 5
根据上面的信息,解答下列问题:
(1)甲组的平均成绩为______分,甲组成绩的中位数是______,
乙组成绩统计图中______,乙组成绩的众数是______;
(2)根据图表信息,请你判断哪个小组的成绩更加稳定?只需要直接写出结论.
31.(2022·江苏泰州·九年级期末)甲、乙两名射击运动员在相同的条件下各打靶10次,每次命中的环数如下:
甲:9,7,8,9,7,6,10,10,6,8;
乙:7,8,8,9,7,8,9,8,.10,6.
(1)甲、乙两名运动员打靶的平均成绩分别是多少
(2)哪名运动员的成绩更为稳定 为什么
32.(2022·江苏泰州·九年级期末)某学校开展防疫知识线上竞赛活动,九年级(1)、(2)班各选出5名选手参加竞赛,两个班选出的5名选手的竞赛成绩(满分为100分)如图所示.
(1)九(1)班竞赛成绩的众数是 ,九(2)班竞赛成绩的中位数是 ;
(2)哪个班的成绩较为整齐,试说明理由.
33.(2022·江苏扬州·九年级期末)某校举办了国学知识竞赛,满分100分,学生得分均为整数.在初赛中,甲乙两组学生成绩如下(单位:分):
甲组:30,60,60,60,60,60,70,90,90,100.
乙组:50,60,60,60,70,70,70,70,80,90.
组别 平均数 中位数 方差
甲组 68 376
乙组 70 116
(1)以上成绩统计分析表中 , ;
(2)小明同学说:“这次竞赛我得了70分,在我们小组中属中游偏上!”观察上面表格判断,小明可能是 组的学生;
(3)如果你是该校国学竞赛的辅导员,你会选择哪一组同学代表学校参加复赛?并说明理由.
34.(2022·江苏镇江·九年级期末)甲、乙两校各有5名学生参加区教育局举办的青少年党史知识竞赛,成绩如下表:
甲校选手得分 97 91 80 91 81
乙校选手得分 76 92 94 86 92
(1)对甲、乙两校参赛学生的成绩进行评价;
(2)如果各校从他们参赛的5名学生中派出前3名参加下一轮的决赛,你认为哪个学校的选手实力更强一些?说说你的理由.
35.(2022·江苏泰州·九年级期末)江苏省第二十届运动会将在泰州召开,某射击队准备从甲、乙二人中选拔1人参加比赛,现将两人在选拔赛中,各射击5次的成绩(单位:环数)绘制成如图所示的折线统计图.(图中只标注了部分射击数据)
观察统计图,回答下列问题:
(1)甲5次射击成绩的中位数为______环;乙5次射击成绩的平均数为______环;
(2)设甲、乙两人5次射击成绩的方差分别为,则______ ;(填“>”、“=”或“<”)
(3)如果你是教练员,你将选择谁去参加省运会?
36.(2022·江苏南京·九年级期末)甲、乙两人在相同的情况下各打靶10次,打靶成绩(单位:环)如下图所示:
(1)填表:
平均数(环) 中位数(环) 方差(环2) 命中9环及9环以上的次数
甲 ▲ 7 1.2 ▲
乙 7 7.5 ▲ 3
(2)从两个不同的角度评价甲、乙两人打靶的成绩.
37.(2022·江苏扬州·九年级期末)八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
38.(2022·江苏扬州·九年级期末)某中学九年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 2号 3号 4号 5号 总数
甲班 100 98 110 89 103 500
乙班 90 97 101 113 99 500
经统计发现两班5名学生踢毽子的总个数相等,此时有学生建议,可以通过考查数据中的其他信息为参考,请你回答下列问题:
(1)甲班比赛数据的中位数为 ,乙班比赛数据的平均数为 ;
(2)计算两班比赛数据的方差;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
39.(2022·江苏扬州·九年级期末)某中学九年级学生共进行了五次体育模拟测试,已知甲、乙两位同学五次模拟测试成绩的均分相同,小明根据甲同学的五次测试成绩绘制了尚不完整的统计表,并给出了乙同学五次测试成绩的方差的计算过程.
甲同学五次体育模拟测试成绩统计表:
次数 第一次 第二次 第三次 第四次 第五次
成绩(分) 25 29 27 a 30
小明将乙同学五次模拟测试成绩直接代入方差公式,计算过程如下:
(分2)
根据上述信息,完成下列问题:
(1)a的值是______;
(2)根据甲、乙两位同学这五次模拟测试成绩,你认为谁的体育成绩更好?并说明理由;
(3)如果甲再测试1次,第六次模拟测试成绩为28分,与前5次相比,甲6次模拟测试成绩的方差将______.(填“变大”“变小”或“不变”)
40.(2022·江苏泰州·九年级期末)某家电销售商店1~6周销售甲、乙两种品牌彩电的数量如图所示(单位:台):
(1)填表:
平均数(台) 方差(台)
甲 ______
乙 10 ______
(2)根据表中数据及折线统计图,对该商店今后采购这两种品牌彩电的意向提出建议,并说明理由.
41.(2022·江苏扬州·九年级期末)为了了解我市两家公司员工的收入情况,某数学兴趣小组的同学对甲、乙两家公司员工月收入进行了一项抽样调查,并将两家公司10名员工月收入(单位:千元)情况进行整理得到下边两幅统计图:
根据以上信息,整理分析数据如表:
平均月收入/千元 中位数 众数 方差
甲公司 a 6.5 6 1.8
乙公司 7 b 7 c
(1)填空:______;______.
(2)求c的值;
(3)某位同学的叔叔决定从两家公司中选择一家去上班,你建议他选哪家公司?说明理由.
42.(2022·江苏连云港·九年级期末)某篮球队在一次联赛中共进行了10场比赛,已知10场比赛的平均得分为88分,且前9场比赛的得分依次为:97、91、85、91、84、86、85、82、88.
(1)求第10场比赛的得分;
(2)求这10场比赛得分的中位数,众数和方差.
43.(2022·江苏连云港·九年级期末)某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是甲班和乙班各5名学生的比赛数据(单位:个):
1号 2号 3号 4号 5号 总数
甲班 89 100 96 118 97 500
乙班 100 95 110 91 104 500
经统计发现两班总数相等.此时有学生建议,可通过考察数据中的其他信息作为参考.
请你回答下列问题:
(1)甲班的优秀率为40%,乙班的优秀率为________;甲班5名学生比赛成绩的中位数是_________个,乙班5名学生比赛成绩的中位数是100个;
(2)求两班比赛数据的方差;
(3)根据以上几条信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.
44.(2022·江苏江苏·九年级期末)九(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟仰卧起坐比赛,在相同的条件下,分别对两名男生进行了七次一分钟仰卧起坐测试.并对数据进行收集、整理:
甲乙两人得分表
序号 1 2 3 4 5 6 7
甲(个分钟) 25 35 36 38 40 46 46
乙(个分钟) 30 33 37 40 40 42 44
下面给出两人测试成绩的统计图表.
甲乙两人得分统计表
平均数 中位数 众数
甲 a 38 46
乙 38 b 40
解答下列问题:
(1)a= ,b= ;
(2)从方差的角度看, 的成绩较稳定(填“甲”或“乙”);
(3)甲、乙都认为自己的成绩更好些,请直接结合统计图表中的信息分别写出他们的理由.
45.(2022·江苏南京·九年级期末)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 众数 中位数 方差
甲 8 8 0.4
乙 9 3.2
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
46.(2022·江苏盐城·九年级期末)某家电销售商店第1~6周甲、乙两种品牌冰箱的周销售量如图所示(单位:台).现将这两种品牌冰箱第1~6周的销售量绘制成如下统计图表
中位数 众数 平均数 方差
甲品牌 10 10
乙品牌 9 10
(1)根据图表信息填空:____________,___________,___________;
(2)根据计算平均数和方差及折线统计图,请你对该商店今后采购这两种品牌冰箱的意向提出建议,并说明理由.
参考答案:
1.B
【解析】商场经理要了解哪些型号最畅销,所关心的即为众数.
解:根据题意知:对商场经理来说,最有意义的是各种型号的衬衫的销售数量,即众数.
故选:B.
本题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
2.C
【解析】根据平均数、中位数、众数和方差的定义逐一求解可得.
A、平均数为,故此选项不符合题意;
B、样本数据为1、2、3、3、6,则中位数为3,故此选项不符合题意;
C、方差为,故此选项符合题意;
D、众数为3,故此选项不符合题意.
故选:C.
本题考查了众数、平均数、中位数、方差.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
3.B
【解析】先计算平均数=3,代入计算即可.
∵1,2,3,4,5,
∴=3,
∴
=2,
故选B.
本题考查了方差,熟练掌握方差的计算公式是解题的关键.
4.B
【解析】根据题意分别计算调整前后的平均数,方差,中位数,极差进而进行判断即可.
解:调整前:平均数为
方差为
中位数为第六个和第七个的平均数:
极差为
调整后:平均数为
方差为
中位数为第六个和第七个的平均数:
极差为
调整前后的平均数,方差,中位数,极差,只有方差发生变化,
故选B
本题考查了求平均数,方差,中位数,极差,掌握求平均数,方差,中位数,极差是解题的关键.
5.B
【解析】根据平均数的定义先求出a的值,再根据方差公式进行计算即可.
解:∵数据1,2,a,3的平均数是3,
∴(1+2+a+3)÷4=3,
∴a=6,
∴这组数据的方差为[(1 3)2+(2 3)2+(6 3)2+(3 3)2]=.
故选:B.
本题考查了方差,一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
6.B
【解析】利用平均数、中位数、方差和标准差的定义对各选项进行判断即可.
解:这组数据的平均数、方差和标准差都与被涂污数字有关,而这组数据的中位数为36与46的平均数,与被涂污数字无关.
故选:B.
本题考查了方差:方差描述了数据对平均数的离散程度.也考查了中位数、平均数和众数的概念.
7.B
【解析】根据平均数,方差的定义计算即可.
解:∵小亮的成绩和其他39人的平均数相同,都是90分,
∴该班40人的测试成绩的平均分为90分,方差变小,
故选:B.
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
8.AB
【解析】根据众数、平均数、方差、中位数的定义解题.
解:根据题意,这组数据出现次数最多的数是25,即众数是25,与被涂污数字无关;
将这组数据按顺序排列,位于正中间的数是,即中位数是24,与被涂污数字无关;平均数与方差的计算结果均与与被涂污数字有关,故计算结果与被涂污数字无关的是:众数、中位数,
故选:AB.
本题考查众数、平均数、方差、中位数等知识,是基础考点,难度较易,掌握相关知识是解题关键.
9.
【解析】先求出3个数的平均数,再根据方差公式计算.
解:数据-1,0,1的平均数:,
方差,
故答案为:.
本题考查方差的计算,方差,熟记方差公式是解题的关键.
10.甲
【解析】根据方差的定义,方差越小数据越稳定.
解:因为S甲2=1.2<S乙2=3.9,方差小的为甲,所以本题中成绩比较稳定的是甲.
故答案为甲;
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
11.乙
【解析】根据方差的意义即方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,数据越稳定,即可得出答案.
解:,,
,
两人射击成绩比较稳定的是乙.
故答案为:乙.
此题主要考查了方差的意义和应用,要熟练掌握,解答此题的关键是要明确:方差越大,表明这组数据偏离平均数越大,数据越不稳定;方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,数据越稳定.
12.乙
【解析】根据方差的意义求解即可.
解:∵甲的方差是0.17,乙的方差是0.05,
∴甲的方差>乙的方差,
∴这5次短跑训练成绩较稳定的是乙,
故答案为:乙.
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也差;反之,则它与其平均值的离散程度越小,稳定性越好.
13.乙
【解析】方差越大,稳定性越差,方差越小,稳定性越好.比较甲乙方差大小可知乙稳定.
解:由题意可知:
∵S乙2<S甲2,
∴净含量较为稳定的是乙,
故答案为:乙.
本题考查利用方差判断稳定性,理解方差越小代表稳定性越好是解本题的关键.
14.甲
【解析】根据成绩图可以得到甲、乙8次打靶的成绩,再根据方差公式代入样本数据计算即可.
解:甲的平均数=(10+7+7+8+8+8+9+7)÷8=8,甲的方差S甲2=[(8-10)2+3×(8-7)2+3×(8-8)2+(8-9)2]÷8=1;
乙的平均数=(10+5+5+8+9+9+8+10)÷8=8,乙的方差S乙2=[2×(8-10)2+2×(8-8)2+2×(8-9)2+2×(8-5)2]÷8=3.5;
∴S甲2<S乙2,
∴甲比乙稳定.
故答案为:甲.
本题考查了平均数和方差的概念,它反映了一组数据的波动大小,方差越大,波动性越大反之也成立.
15.甲
【解析】根据方差的定义,方差越小数据越稳定即可求解.
解:∵,
∴方差最小的为甲,
∴成绩更稳定的是甲.
故答案为:甲.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
16.①③##③①
【解析】根据方差、平均数、中位数的概念求解.
解:①若a=22,则A的平均数为=23,
B的平均数,
∴A的平均数大于B的平均数,正确;
②若a=23,则A的平均数为=23,
A的方差:×[(23-21)2+(23-22)2+(23-23)2+(23-24)2+(23-25)2]=2,
B的平均数,
B的方差:×[(23-21)2+(23-22)2+(23-23)2+(23-24)2+(23-25)2+(23-23)2]=,
∴A的方差不等于B的方差,错误;
③若a=24,则A的中位数为23,
B的中位数=23.5.
∴A的中位数小于B的中位数,正确.
故答案为:①③.
本题考查了方差、众数、平均数、中位数的知识,解答本题的关键是掌握各知识点的概念.
17.
【解析】根据平均数的性质,通过列一元一次方程并求解,即可得;再根据方差的性质计算,即可得到答案.
∵一组数据1,2,3,.它们的平均数是2,
∴
∴
∴这一组数据的方差为:
故答案为:.
本题考查了数据分析、一元一次方程的知识;解题的关键是熟练掌握平均数和方差的性质,从而完成求解.
18.②③##③②
【解析】分别计算出三个样本的平均数及方差,根据方差越小离散程度越小即可判断.
解:根据平均数,方差的计算方法,依次计算如下:
样本1的平均数,
方差,
样本2的平均数,
方差,
样本3的平均数,
方差,
,
样本2的方差最小,即样本2的离散程度最小,故②正确;
三数数据的离散程度从小到大一次为:样本2、样本3、样本1,故③正确;
样本1与样本3的离散程度不相同,故①错误;
故答案为:②③.
本题考查了方差,解题的关键是掌握求方差的基本公式及方法.
19.甲.
【解析】先计算出甲的平均数,再计算甲的方差,然后比较甲乙方差的大小可判定谁的成绩稳定.
甲的平均数,
所以甲的方差,
因为甲的方差比乙的方差小,
所以甲的成绩比较稳定.
故答案为甲.
本题考查方差的定义:一般地设n个数据,,,…,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
20.>
【解析】根据甲、乙两组数据分别求出甲、乙的平均数,然后再利用方差公式进行求解比较即可.
解:由题意得:
,,
∴,
,
∴,
∴;
故答案为>.
本题主要考查平均数及方差,熟练掌握平均数及方差的计算是解题的关键.
21.3
【解析】根据方差的计算公式即可得出答案.
解:∵,
∴这组数据的平均数是3,
故答案为:3.
本题主要考查方差,解题的关键是掌握方差的定义及其计算公式.
22.2
【解析】将第二组数据中的每一个数据均减去2020后得到一组新数据与甲数据相等,由此可以得到两组数据的方差相同.
解:将数据:2021、2022、2023、2024、2025都减去2020后得到数据1、2、3、4、5,
与数据:1、2、3、4、5的方差相同,是2
故答案为:2.
本题考查了方差,牢记方差的变化规律是解决此类问题的关键.
23.(1)85;70;85;100
(2)理由见解析
【解析】(1)从图上读取信息,由平均数、中位数、众数、方差的定义即可得到答案.
(2)对比七、八年级的相关数据,从中位数、方差的意义分析即可得到答案.
(1)
解:
平均数(分) 中位数(分) 众数(分) 方差
七年级 85 85 85 70
八年级 85 80 100 160
(2)
解:①七年级成绩的方差低于八年级,成绩比八年级稳定,
②七年级的中位数比八年级高,所以七年级成绩好一些.
本题考查平均数、中位数、众数、方差的定义及其意义,熟练掌握相关知识是解题的关键.
24.(1)m=90,n =90,p =90
(2)30
(3)八年级的学生成绩好,见解析
【解析】(1)由中位数、众数、平均数的定义求解即可得出答案;
(2)根据方差的定义列式计算即可;
(3)在七、八年级学生成绩的中位数和众数相同的前提下,根据平均数和方差的意义即可判断;
(1)
解:七年级的中位数为=90分,故m=90;
八年级的平均数为:×(85+85+95+80+95+90+90+90+100+90]=90,故n=90;
八年级中90分的最多,故p=90;
(2)
解:八年级的方差q=×[(80﹣90)2+2×(85﹣90)2+4×(90﹣90)2+2×(95﹣90)2+(100﹣90)2]=30;
(3)
解:八年级的学生成绩好,
理由如下:七、八年级学生成绩的中位数和众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更稳定,
综上,八年级的学生成绩好;
本题考查了中位数、众数、平均数、方差等统计基础知识,明确相关统计量表示的意义及相关计算方法是解题的关键.
25.(1)8.5,8,8.5,0.7;(2)甲班的成绩更稳定.
【解析】(1)根据平均数和众数的概念求出甲的平均数与众数,根据方差的计算公式求出甲的方差;
(2)根据方差的性质解答.
解:(1)甲的平均数为=8.5,众数为:8.5,
方差为:[(8.5﹣8.5)2+(7.5﹣8.5)2+(8﹣8.5)2+(8.5﹣8.5)2+(10﹣8.5)2]=0.7,
乙的中位数是8,
(2)从方差看,甲班的方差小,所以甲班的成绩更稳定.
此题主要考查统计调查的应用,解题的关键是熟知平均数、方差、众数及中位数的求解方法.
26.(1)8;8;7.5;(2)甲班的成绩更加稳定
【解析】(1)分别求出甲、乙两班的平均数、中位数、众数,即可得到答案;
(2)分别求出甲、乙两个班的方差,即可进行判断.
解:(1)甲班的众数为:8;
乙班的平均数为:;
乙班的中位数为:;
故答案为:8;8;7.5;
(2)甲班的方差为:
;
乙班的方差为:
;
∵,
∴,
∴甲班的成绩更加稳定;
本题考查了利用方差判断稳定性,也考查了加权平均数、众数、中位数,解题的关键是熟练掌握所学的知识,正确的进行数据的处理.
27.(1)8,8,.
(2)选择小华参赛,理由见解析.
(3)变小.
【解析】(1)根据平均数、中位数、方差的计算方法分别计算即可;
(2)通过平均数、方差的大小,得出结论;
(3)计算出小亮再射击2次后8次的平均数、方差,通过方差的比较得出答案.
(1)
解:小华的平均成绩(环),
小华的方差(环),
把小亮的成绩从小到大排列为5,7,8,8,10,10,
则中位数(环),
故答案为:8,8,.
(2)
解:∵小亮的方差是3,小华的方差是,即,
又∵小亮的平均数和小华的平均数相等,
∴选择小华参赛.
(3)
解:小亮再射击后的平均成绩是(环),
射击后的方差是:,
∴小亮这8次射击成绩的方差变小,
故答案为:变小.
此题考查平均数、中位数、方差的意义和计算方法,明确各个统计量的意义及反应数据的特征是正确解答的关键.
28.(1)8,8
(2)小华,理由见解析
(3)环2
【解析】(1)根据平均数、中位数的计算方法分别计算即可;
(2)通过平均数、方差的大小,得出结论;
(3)计算出小亮再射击后的平均数、方差即可得出答案.
(1)
解:小华的平均成绩为a=(6+7+7+9+9+10)÷6=8(环),
把小亮的成绩从小到大排列为5,7,8,8,10,10,
则中位数为=8(环),
故答案为:8,8;
(2)
解:选择小华参赛,理由如下:
∵小亮的方差是3,小华的方差是2,即3>2,而小亮的平均数和小华的平均数相等,
∴小华的成绩稳定,
∴选择小华参赛;
(3)
解:小亮再射击后的平均成绩是(8×6+7+9)÷8=8(环),
射击后的方差是:
×[(5-8)2+(7-8)2×2+(8-8)2×2+(10-8)2×2+(9-8)2]=2.5(环2).
此题考查平均数、中位数、方差的意义和计算方法,明确各个统计量的意义及反应数据的特征是正确解答的关键.
29.(1)8,8
(2)九(1)班5名同学比赛成绩的方差
(3)从数据的集中程度平均数来看,九(2)班五名同学在比赛中的表现更加优秀;从数据的离散程度方差来看,九(2)班五名同学在比赛中表现更加优秀
【解析】(1)将数字从左往右依次排列,出现次数最多的数字为众数,数据中居于中间位置的数叫做中位数;
(2)若的平均数为m,则方差公式可表示为: ,根据方差公式计算方差即可;
(3)答案不唯一,选择数据的某一方面的特点加以分析即可.
(1)
解:将数据由小到大排列为:5,8,8,9,10
则由数据可知众数为:8,
中位数为:8,
故答案为:8;8 .
(2)
九年级(1)班参赛选手的平均成绩=(8+10+8+9+5)÷5=8(次),
则方差S2=×(0+4+0+1+9)=.
(3)
答案不唯一
①如从数据的集中程度平均数来看,因为九(2)班平均成绩高于九(1)班,所以九(2)
班五名同学在比赛中的表现更加优秀;
②从数据的离散程度方差来看,因为九(2)班五名同学成绩的方差小于九(1)班,所以九(2)班五名同学表现更加稳定,且九(2)班平均成绩高于九(1)班,所以九(2)班五名同学在比赛中表现更加优秀.
本体考察数据的收集与整理,能熟练掌握方差的求法,并根据数据的特点对提供数据的事件进行分析是解决本体的关键.
30.(1)8.7;8.5;3;8
(2)乙组
【解析】(1)用总人数减去其他成绩的人数,求出m,再根据中位数和众数的定义即可求出甲组成绩的中位数和乙组成绩的众数;
(2)先求出平均数,再根据方差公式求出甲、乙组的方差,然后进行比较,即可得出答案.
(1)
(1)甲组的平均成绩为: = 8.7(分),
甲组成绩的中位数是= 8.5(分),
乙组成绩统计图中m= 20- (2 +9+6)= 3,
乙组成绩的众数是8分,
故答案为: 8.7, 8.5分, 3, 8分;
(2)
(2)乙组的成绩更加稳定,
甲组的方差为:
[(7-8.7)2 +9×(8-8.7)2 +5×(9- 8.7)2 +5×(10- 8.7)2]= 0.81,
乙组平均成绩是: ×(2×7+9×8+6×9+3×10)= 8.5(分),
乙组的方差为:
[2×(7-8.5)2+9×(8-8.5)2+6×(9-8.5)2+3×(10-8.5)2]=0.75,
∴<
所以乙组的成绩更稳定.
此题考查了平均数、众数和中位数,方差的有关内容,解题的关键是正确理解统计图,学会计算方差.
31.(1),
(2)乙更稳定,理由见解析
【解析】(1)根据平均数的公式:平均数=所有数之和再除以数的个数;
(2)先根据方差公式进行计算,方差越大,波动越大,成绩越不稳定,射击水平越差,反之也成立.
(1)
解:甲、乙两人射击成绩的平均成绩分别为:
;
.
(2)
,
,
∵,
∴乙更稳定.
本题考查平均数和方差的计算,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.平均数反映了一组数据的集中程度,求平均数的方法是所有数之和再除以数的个数;方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法.
32.(1)80分,85分
(2)九(1)班成绩较为整齐,理由见解析
【解析】(1)根据众数和中位数的概念求解即可;
(2)根据方差的定义和意义求解即可.
(1)
解:由图知,九(1)班成绩为80、80、80、90、100,
九(2)班成绩为70、80、85、95、100,
所以九(1)班成绩的众数为80分,九(2)班成绩的中位数为85分;
故答案为:80分,85分.
(2)
解:九(1)班成绩较为整齐,理由如下:
∵九(1)班成绩的平均数为=86(分),
九(2)班成绩的平均数为=86(分),
∴九(1)班成绩的方差为×[3×(80-86)2+(90-86)2+(100-86)2]=64,
九(2)班成绩的方差为×[(70-86)2+(80-86)2+(85-86)2+(95-86)2+(100-86)2]=114,
∴九(1)班成绩较为整齐.
本题主要考查条形统计图、众数、中位数和方差,解题的关键是掌握众数、中位数和方差的定义以及方差的意义.
33.(1)60,68
(2)甲
(3)选乙组参加复赛,理由见解析
【解析】(1)根据平均数和中位数的定义分别进行解答即可得出答案;
(2)根据中位数的意义即可得出答案;
(3)根据方差的意义即可得出答案.
(1)
解:把甲组的成绩从小到大排列为,最中间的数是=60(分),
则中位数a=60分;
b=×(50+60+60+60+70+70+70+70+80+90)=68(分),
故答案为:60,68;
(2)
解:小明可能是甲组的学生,理由如下:
因为甲组的中位数是60分,而小明得了70分,所以在小组中属中游略偏上,
故答案为:甲;
(3)
解:选乙组参加复赛.理由如下:
∵S甲2=376>S乙2=116,
∴乙组的成绩比较稳定,而且乙组的中位数大于甲组的中位数,
选乙组参加复赛.
本题考查了平均数,中位数,方差的意义.平均数平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
34.(1)甲、乙两校的平均分相等,甲校的方差小于乙校的方差,因此甲校学生的成绩较稳定,成绩较好
(2)甲校的平均分高于乙校,因此甲校的选手实力更强些
【解析】(1)计算甲、乙两校参赛学生成绩的平均分,众数,中位数,方差,再进行分析即可;
(2)计算各校前3名的平均分,比较即可.
(1)
解:由表中数据可知,甲校的平均分是=88(分),
众数是91,
中位数是91,
方差是×[(88-97)2+(88-91)2+(88-80)2+(88-91)2+(88-81)2]=42.4;
乙校的平均分是=88(分),
众数是92,
中位数是92,
方差是×[(88-76)2+(88-92)2+(88-94)2+(88-86)2+(88-92)2]=43.2.
甲、乙两校的平均分相等,甲校的方差小于乙校的方差,因此甲校学生的成绩较稳定,成绩较好;
(2)
甲校派出选手的成绩为91、91、97,平均分是,
乙校派出选手的成绩为92、92、94,平均分是,
甲校的平均分高于乙校,因此甲校的选手实力更强些.
本题考查了方差、众数、中位数以及平均数,掌握方差、众数、中位数以及平均数的定义是解题的关键.
35.(1),
(2)
(3)选择乙去参加省运会,理由见解析
【解析】(1)根据中位数、平均数的定义分别进行解答即可得出答案;
(2)根据方差的意义,结合折线统计图即可求解;
(3)根据中位数、方差的意义即可得出答案.
(1)
解:(1)把甲5次射击成绩按从小到大的顺序排列,第3个数是8.2,所以甲5次射击成绩的中位数为8.2环;
乙5次射击成绩为:,,,,,
平均数为环;
故答案为:,;
(2)
解:根据折线图可知,乙5次射击成绩与其平均值的偏离程度较小,成绩更稳定,即.
故答案为: ;
(3)
解:选择乙去参加省运会,理由如下:
因为乙的中位数是8.4环,高于甲的中位数,而且,乙的成绩比甲更稳定,
所以应选乙去参加省运会.
本题考查了折线统计图.读懂统计图,从统计图中得到必要的信息是解决问题的关键.也考查了中位数、平均数和方差的意义.
36.(1)7; 5.4; 1
(2)甲打靶的成绩更稳定,(答案不唯一)理由见解析
【解析】(1)根据图象将甲乙打靶成绩都写出来,然后依据平均数及方差的计算方法求解即可;
(2)评价方法可以从平均数或者方差方面进行分析即可.
(1)
解:由图可得甲的打靶环数分别为:9,5,7,8,7,6,8,6,7,7,
∴甲打靶的平均成绩为:
,
乙的打靶环数分别为:2,4,6,8,7,7,8,9,9,10,
∴乙打靶的方差为:
=5.4;
甲成绩中命中9环及以上的只有1次,
故答案为:7;5.4;1;
(2)
本题答案不唯一,下列解法供参考.例如:
①甲、乙打靶的成绩的平均数都是7环,说明两人的打靶实力相当;
②甲、乙两人打靶的成绩的方差分别是1.2环2和5.4环2,说明甲打靶的成绩更稳定.
题目主要考查计算数据的平均数及方差,利用平均数或方差作决策等,理解题意,熟练掌握运用平均数及方差的计算方法是解题关键.
37.(1)9.5,10;(2)平均成绩9分,方差1;(3)乙
【解析】(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙队的平均成绩,再根据方差公式进行计算;
(3)先比较出甲队和乙队的方差,再根据方差的意义即可得出答案.
解:(1)把甲队的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),
则中位数是9.5分;
乙队成绩中10出现了4次,出现的次数最多,
则乙队成绩的众数是10分;
故答案为:9.5,10;
(2)乙队的平均成绩是:×(10×4+8×2+7+9×3)=9,
则方差是:×[4×(10﹣9)2+2×(8﹣9)2+(7﹣9)2+3×(9﹣9)2]=1;
(3)∵甲队成绩的方差是1.4,乙队成绩的方差是1,
∴成绩较为整齐的是乙队;
故答案为:乙.
本题考查方差、中位数和众数:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1 )2+(x2 )2+…+(xn )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
38.(1)100,100
(2),
(3)应该把团体第一名的奖状给甲班,因为甲班和乙班的平均数相同,甲班的方差比乙班低,甲班比较稳定,综合评定甲班比较好
【解析】(1)
解:甲班的成绩重新排列为:89,98,100,103,110,故中位数为100,
乙班成绩的平均数为,
故答案为:100,100;
(2)
甲的平均数为:500÷5=100(个),
S甲2=[(100﹣100)2+(98﹣100)2+(110﹣100)2+(89﹣100)2+(103﹣100)2]÷5=46.8;
乙的平均数为:500÷5=100(个),
S乙2=[(90﹣100)2+(97﹣100)2+(101﹣100)2+(113﹣100)2+(99﹣100)2]÷5=56;
(3)
应该把团体第一名的奖状给甲班,理由如下:因为甲班和乙班的平均数相同,甲班的方差比乙班低,甲班比较稳定,综合评定甲班比较好.
此题考查了统计计算,正确掌握中位数的定义,平均数的计算公式,方差的计算公式,利用方差做决策是解题的关键.
39.(1)29
(2)乙的体育成绩更好,理由见解析
(3)变小
【解析】(1)根据平均分相同,根据乙的方差公式可得乙的平均分为28,则甲的平均分也为28,进而求得的值;
(2)根据甲的成绩计算甲的方差,比较甲乙的方差,方差小的体育成绩更好;
(3)根据第六次的成绩等于平均数,根据方差公式可知方差将变小.
(1)
解:甲、乙两位同学五次模拟测试成绩的均分相同,
乙的方差为:
则平均分为28
所以甲的平均分为28
则
解得
故答案为:29
(2)
乙的成绩更好,理由如下,
乙的成绩较稳定,则乙的体育成绩更好
(3)
甲6次模拟测试成绩的方差将变小
故答案为:变小
本题考查了求方差,平均数,根据方差判断稳定性,掌握求方差的公式是解题的关键.
40.(1)10,
(2)甲品牌,理由见解析
【解析】(1)先通过折线图获得数据,后利用平均数的计算公式,方差计算公式分别计算即可;
(2)选择从平均数,方差等统计特征量的角度去分析,答案不是唯一的,只要合理即可.
(1)
∵甲的数据为:7,10,8,10,12,13,
∴=10,
∵乙的数据为:9,10,11,9,12,9,,
∴
=,
故答案为:10,.
(2)
两种品牌的彩电的周平均销售量相同,乙品牌彩电周销售量的方差较小,说明乙品牌的彩电周销售量比较稳定,从折线统计图看,甲品牌的彩电的周销售量呈上升趋势,建议商家可以多采购甲品牌的彩电(答案是开放的,言之有理即).
本题考查了折线统计图,平均数,方差,根据统计图获得信息,并熟练进行相关的计算是解题的关键.
41.(1)7,7
(2)1.4
(3)选乙公司,理由见解析
【解析】(1)利用平均数、中位数的定义分别计算后即可确定正确的答案;
(2)利用方差的计算公式进行计算后即可确定正确的答案;
(3)根据平均数一样,中位数及众数的大小和方差的大小进行选择即可.
(1)
甲公司员工月收入6千元占比为:
甲公司员工的平均月收入为:(千元)
∴
乙公司员工月收入从小至大排列为:5,5,7,7,7,7,7,8,8,9,
∴中位数为7
∴
故答案为:7,7
(2)
∵
∴
∴
(3)
选乙公司,理由如下:
因为月收入平均数一样,中位数、众数乙公司大于甲公司,且乙公司方差小,更稳定.
本题考查了求平均数、中位数、众数和方差,解题的关键是能够了解有关的计算公式.
42.(1)91;(2)中位数为87分,众数为91分和方差18.2分.
【解析】(1)根据平均数的定义求出第10场比赛的得分;
(2)再根据中位数、众数的定义、方差公式求出中位数、众数和方差.
解:(1)解:设第10场比赛得分为x,
根据题意知,(97+91+85+x+91+84+86+85+82+88)÷10=88,
解得x=91,
所以第10场比赛得分91分;
(2)在这一组数据中91是出现次数最多的,故众数是91;
将这组数据从小到大的顺序排列(82,84,85,85,86,88,91,91,91,97),处于中间位置的数是86、88,
由中位数的定义可知,这组数据的中位数是(86+88)÷2=87,
,
故这10场比赛得分的中位数为87分,众数为91分和方差18.2分.
此题考查了平均数、众数与中位数和方差.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;众数是一组数据中出现次数最多的数;一般地设n个数据,x1,x2,…xn的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
43.(1)60%;97;
(2)94;44.4
(3)冠军奖杯应发给乙班,理由见解析
【解析】(1)优秀率就是优秀的人数与总人数的百分比;
(2)根据平均数和方差的概念计算.
(3)根据计算出来的统计量的意义分析判断.
(1)
乙班的优秀率:×100%=60%;
把甲班5名同学踢的个数从小到大排列为:89,96,97,100,118,
则甲班5名学生比赛成绩的中位数是97个;
故答案为:60%;97;
(2)
甲班的平均数是:(89+100+96+118+97)÷5=100(个),
甲班的方差
乙班的平均数是:(100+95+110+91+104)÷5=100(个),
乙班的方差;
(3)
冠军奖杯应发给乙班,理由如下:
因为两班总数相等,但乙班5名学生的比赛成绩的优秀率比甲班高,中位数比甲班大,方差比甲班小,成绩更稳定,综合评定乙班踢毽子水平较好.
本题考查了中位数、平均数和方差等概念以及运用.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动.
44.(1)38,40
(2)乙
(3)见解析
【解析】(1)根据平均数的计算公式及中位数的定义解答;
(2)根据折线图直接得到答案;
(3)根据表格中的数据分析得到比较即可.
(1)
解:38,b=40,
故答案为:38,40;
(2)
解:由甲、乙两人得分的大小波动情况,直观可得,
∴乙的得分较稳定.
故答案为:乙;
(3)
甲的成绩更好些,理由为:甲得分的众数比乙的高.
乙的成绩更好些,理由为:乙得分的中位数比甲的高.(或写乙得分较稳定也可以).
此题考查了统计知识,掌握平均数的计算公式,中位数的定义,分析比较折线统计图及统计表得到相关数据,正确掌握各知识点并应用是解题的关键.
45.(1)填表见解析;(2)理由见解析;(3)变小.
【解析】(1)根据众数、平均数和中位数的定义求解:
(2)方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
(3)根据方差公式求解:如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
解:(1)根据数据可得:甲的众数为8,
乙的平均数=(5+9+7+10+9)=8,
将乙的数据重新排序为:5,7,9,9,10
乙的中位数为9;
故填表如下:
平均数 众数 中位数 方差
甲 8 8 8 0.4
乙 8 9 9 3.2
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)如果乙再射击1次,命中8环,平均数不变,
则乙的方差为,
所以乙的射击成绩的方差变小.
题目主要考查众数、平均数和中位数的求法,利用方差作决策等,理解题意,熟练掌握运用各个数据的求法是解题关键.
46.(1)9.5,10,
(2)见解析
【解析】(1)先根据图表,确定数据,后根据所求,逐一计算即可.
(2) 比较后,提出合理化的建议即可.
(1)
∵甲品牌的数据为:7,10,8.,10,12,13,
∴,
∴b=10,
∴=,
∴c=,
∵乙品牌的数据为:9,10,11.,9,12,9,
∴9,9,9,10,11., 12,
∴中位数为:=9.5,
∴a=9.5,
故答案为:9.5,10,.
(2)
甲、乙两种品牌冰箱周销售量的平均数相同,而乙品牌冰箱周销售量的方差较小,说明乙品牌冰箱周销售量比较稳定,所以可选择采购乙品牌的冰箱;从折线图来看,甲品牌冰箱的月销售量呈上升趋势,所以进货时可多进甲品牌冰箱.
本题考查了平均数,中位数,方差,熟练从图表中获取解题信息并灵活运用公式计算是解题的关键.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
