7.5三角形内角和定理(2)课件

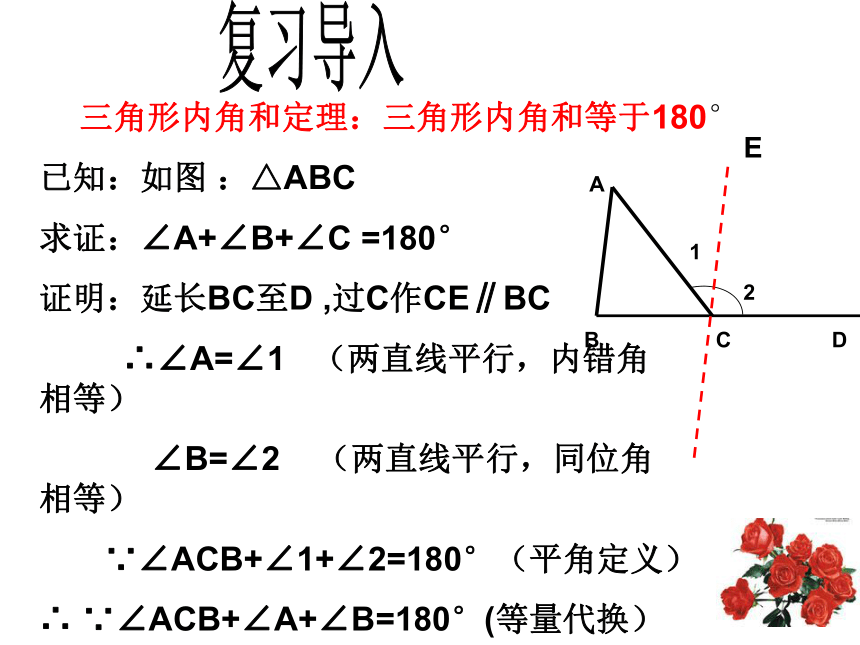
课件15张PPT。7.5三角形内角和定理(2)三角形内角和定理：三角形内角和等于180°已知：如图 ：△ABC
求证：∠A+∠B+∠C =180°
证明：延长BC至D ,过C作CE∥BC
∴∠A=∠1 （两直线平行，内错角
相等）
∠B=∠2 （两直线平行，同位角
相等）
∵∠ACB+∠1+∠2=180°（平角定义）
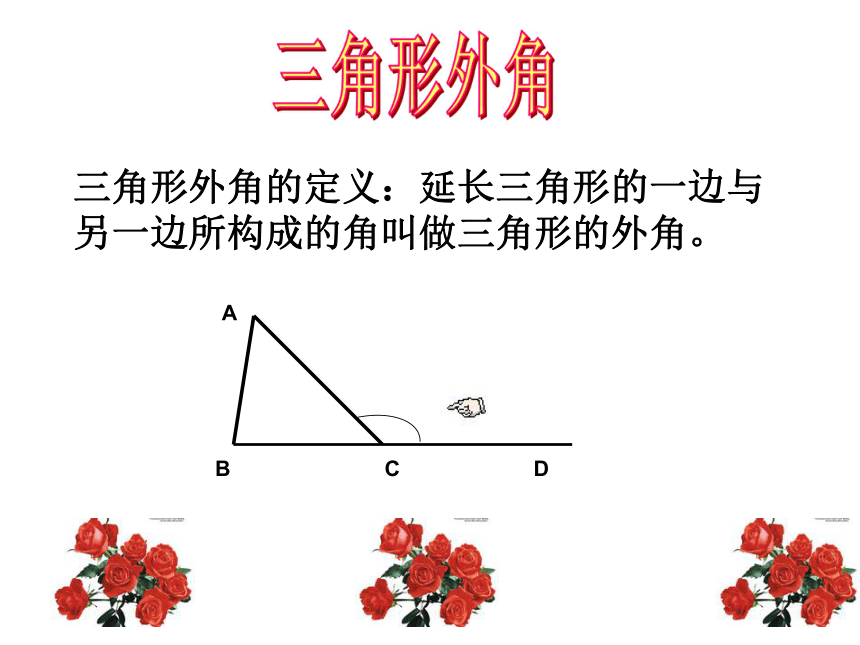
∴ ∵∠ACB+∠A+∠B=180°(等量代换）12E复习导入三角形外角的定义：延长三角形的一边与另一边所构成的角叫做三角形的外角。三角形外角 外角的特征有三条：
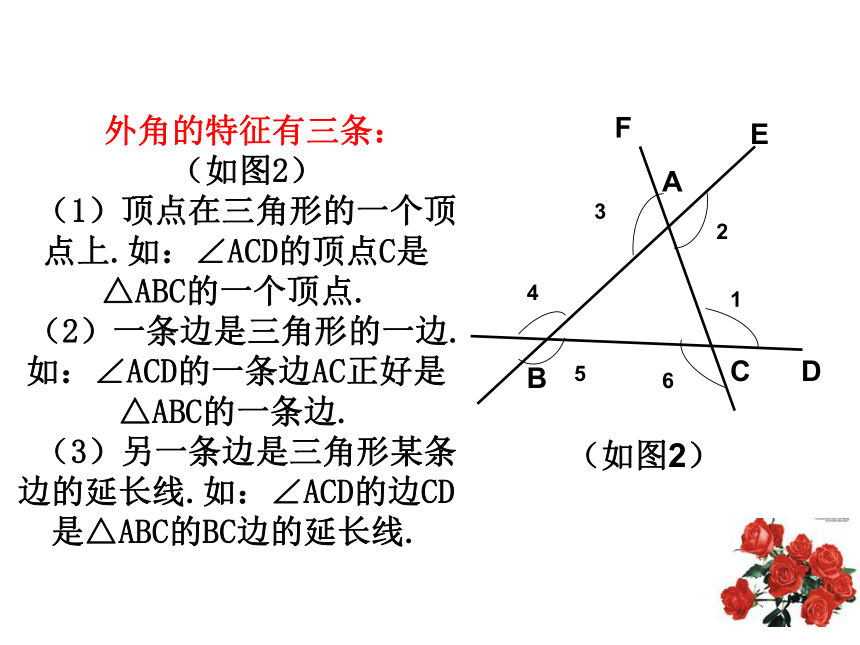
（如图2）
（1）顶点在三角形的一个顶点上.如：∠ACD的顶点C是△ABC的一个顶点.
（2）一条边是三角形的一边.如：∠ACD的一条边AC正好是△ABC的一条边.
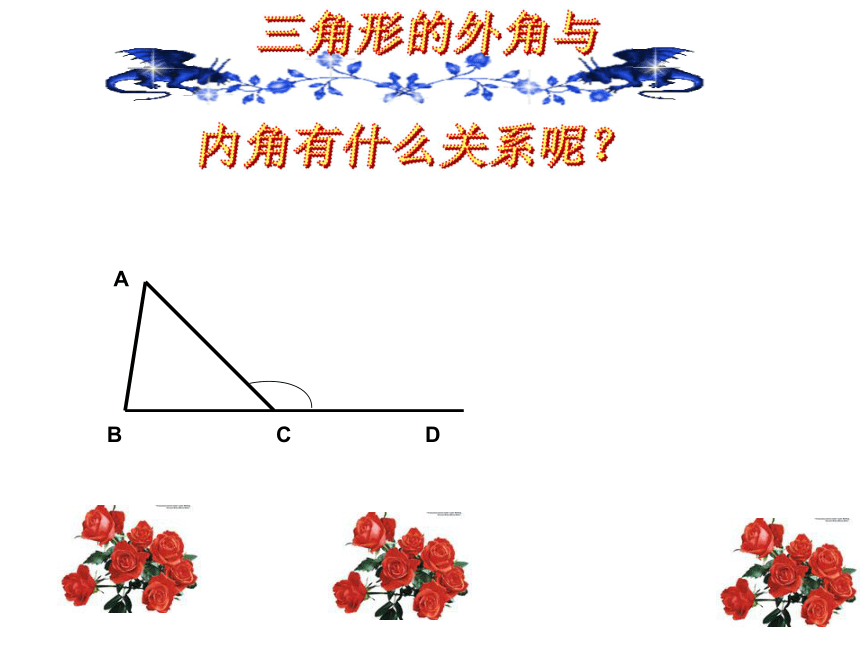
（3）另一条边是三角形某条边的延长线.如：∠ACD的边CD是△ABC的BC边的延长线.（如图2）三角形的外角与
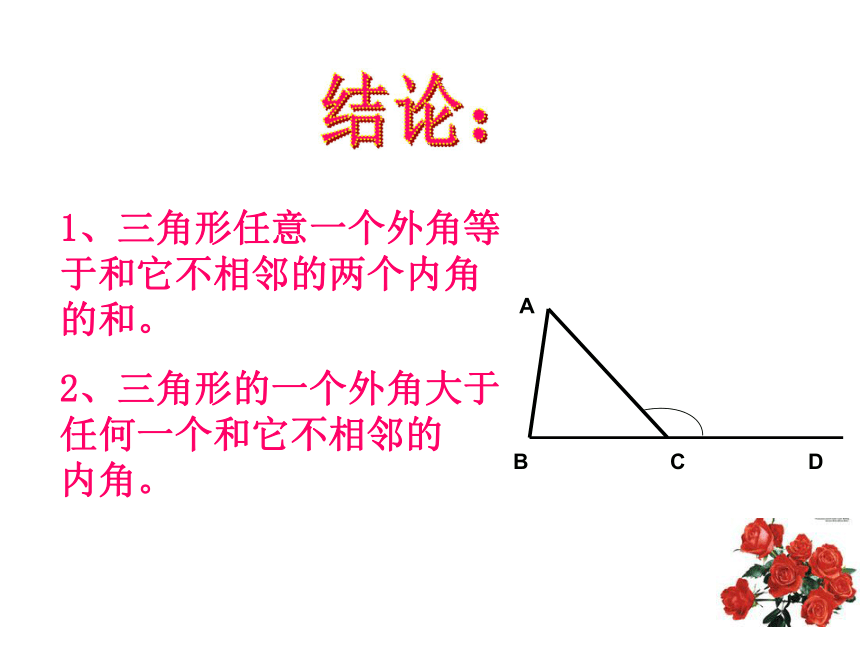
内角有什么关系呢？1、三角形任意一个外角等于和它不相邻的两个内角的和。
2、三角形的一个外角大于任何一个和它不相邻的
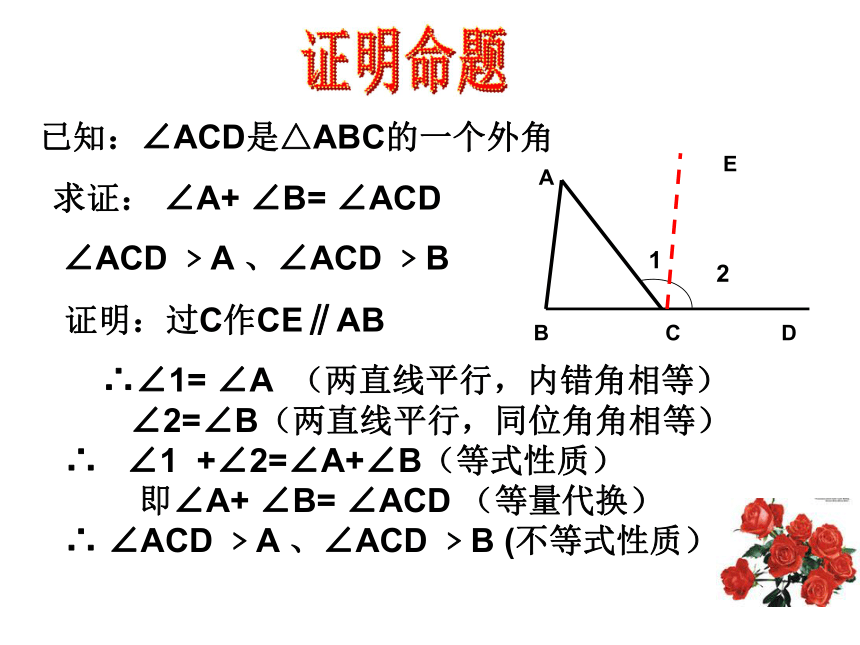
内角。结论：12E已知：∠ACD是△ABC的一个外角证明命题求证： ∠A+ ∠B= ∠ACD
∠ACD ﹥A 、∠ACD ﹥B 证明：过C作CE∥AB
∴∠1= ∠A （两直线平行，内错角相等）
∠2=∠B（两直线平行，同位角角相等）
∴ ∠1 +∠2=∠A+∠B（等式性质）
即∠A+ ∠B= ∠ACD （等量代换）
∴ ∠ACD ﹥A 、∠ACD ﹥B (不等式性质）
1、三角形任意一个外角等于和它不相邻的 两个内角的和。
2、三角形的一个外角大于任何一个和它不相邻的内角。推论由一个公理或定理直接推出的定理叫做这个公理或定理的推论。符号语言：
∵∠ACD是△ABC的一个外角∴∠A+ ∠B= ∠ACD （三角形的外角等于和它不相邻的两个内角的和）
∠ACD ﹥A 、∠ACD ﹥B
（三角形的一个外角大于和它不相邻的任何一个外角）问题1、已知：在△ABC中，∠B=∠C, AD平分外角∠EAC,
求证：AD∥BC理解运用：证明：∵∠EAC是△ABC的一个外角（已知）
∴∠EAC=∠B+∠C
(三角形一个外角等于和它不相邻的两个内角的和）
∠B=∠C （已知）
∴∠EAC=2∠C （等量代换）
∵AD平分∠EAC (已知）
∴∠EAC=2∠1（角平分线定义）
∴ 2∠1 =2∠C （等量代换）
∴ ∠1 =∠C （等式性质）
∴ AD∥BC （内错角相等，两直线平行）
1理解运用：理解运用：问题2：在△ABC中，∠1是它的一个外角，E为边AC上的一点，延长BC到D,连接DE
求证：∠1＞∠2证明：∵∠EAC是△ABC的一个外角（已知）
∴∠1＞∠3(三角形一个外角大于和它不相邻的任何一个外角）
∵∠3是△CDE的一个外角（外角定义）
∴ ∠3＞∠2
(三角形一个外角大于和
它不相邻的任何一个外角）

∴∠1＞∠2 (不等式性质）理解运用：理解运用：问题3：已知如图：P是△ABC内的一点，求证：∠BPC＞∠AE证明：延长BP交AC于E
∵∠BPC是△ABC的外角（三角形外角定义）
∴∠BPC＞∠PEC（三角形一个外角，大于和它不相邻的任何一个
外角）
同理可证：∠PEC＞∠A
∴∠BPC＞∠A(不等式性质）1、三角形任意一个外角等于和它不相邻的 两个内角的和。
2、三角形的一个外角大于任何一个和它不相邻的内角。符号语言：
∵∠ACD是△ABC的一个外角∴∠A+ ∠B= ∠ACD （三角形的外角等于和它不相邻的两个内角的和）
∠ACD ﹥A 、∠ACD ﹥B
（三角形的一个外角大于和它不相邻的任何一个外角）再见