2.1 整式 导学案(含答案)-2022—2023学年人教版数学七年级上册
文档属性
| 名称 | 2.1 整式 导学案(含答案)-2022—2023学年人教版数学七年级上册 |

|
|
| 格式 | zip | ||
| 文件大小 | 139.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览

文档简介
2.1整式
【学习目标】
理解字母表示数的意义,会用含有字母的式子表示实际问题中的数量关系;经历用含有字母的式子表示实际问题的数量关系的过程,体会从具体到抽象的认识过程,发展符号意识。
【学习重难点】
学习重点:理解字母表示数的意义,正确分析实际问题中的数量关系,并用含有字母的式子表示数量关系,感受其中“抽象”的数学思想。
学习难点:把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来。
【学习过程】
一、自主学习
1.议一议:列车在冻土地段行驶2小时的路程是多少千米?3小时又是多少千米?t小时呢?(说明:在含有字母的式子中如果出现乘号,通常将乘号写作“·”或省略不写。例如:100×t可以写成100·t或100t)
2.回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
二、合作探究
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是acm,高是hcm,用式子表示它的体积;
(4)用式子表示数n的相反数。
三、精讲释疑
(1)一条河的水流速度是2.5km/h,船在静水中的速度是vkm/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
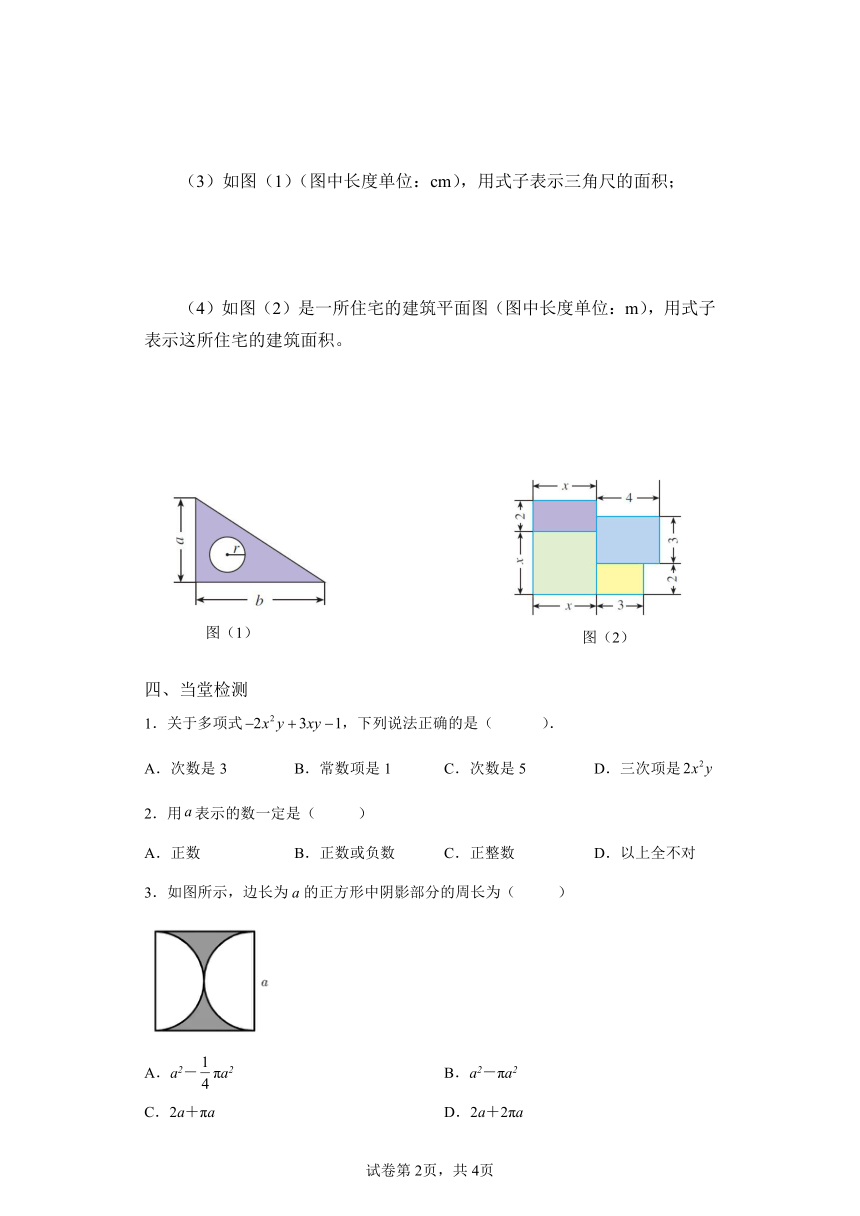
(3)如图(1)(图中长度单位:cm),用式子表示三角尺的面积;
(4)如图(2)是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积。
四、当堂检测
1.关于多项式,下列说法正确的是( ).
A.次数是3 B.常数项是1 C.次数是5 D.三次项是
2.用表示的数一定是( )
A.正数 B.正数或负数 C.正整数 D.以上全不对
3.如图所示,边长为a的正方形中阴影部分的周长为( )
A.a2-πa2 B.a2-πa2
C.2a+πa D.2a+2πa
4.下列说法中正确的有( )个.
①的系数是7;②与没有系数;③的次数是5;
④的系数是;⑤的次数是;⑥的系数是.
A.0 B.1 C.2 D.3
5.将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A.98 B.100 C.102 D.104
6.篮球队要购买10个篮球,每个篮球元,一共需要__________元.(用含的代数式表示)
7.观察下列等式:,,,…按此规律,则第个等式为__________________.
8.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形中共有________个〇.
9.某花卉基地购买了一批水培植物营养液,已知甲种营养液每瓶2L,乙种营养液每瓶3L.
(1)若花卉基地购买了甲种营养液m箱(每箱12瓶),乙种营养液n箱(每箱10瓶),共QL.用含m,n的式子表示Q;
(2)若购进甲种营养液瓶,乙种营养液瓶,用科学记数法表示Q.
10.【做一做】列代数式
(1)已知一个三位数的个位数字是a,十位数字是b,百位数字是c,则这个三位数可表示为 ;
(2)某地区夏季高山的温度从山脚处开始每升高100米,降低0.7℃,若山脚温度是28℃,则比山脚高x米处的温度为 ℃;
(3)已知某礼堂第1排有18个座位,往后每一排比前一排多2个座位.则第n排共有座位数 个.
【数学思考】
(4)上面所列的代数式都属于我们所学习的整式中的 ;
(5)请你任意写一个关于x的这种类型的数字系数的二次式 ;
(6)用字母表示系数,写一个关于x的二次三项式,并注明字母系数应满足的条件 ;
【问题解决】
(7)若代数式3x|m|﹣(m﹣2)x+4是一个关于x的二次三项式,求m的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.D
3.C
4.B
5.B
6.
7..
8.6055
9.(1)
(2)
10(1)100c+10b+c;(2)(﹣0.007x+28);(3)(2n+16);(4)多项式;(5) x2+1;(6)ax2+bx+c(a、b、c均不为0);(7)-2.
7 / 7
【学习目标】
理解字母表示数的意义,会用含有字母的式子表示实际问题中的数量关系;经历用含有字母的式子表示实际问题的数量关系的过程,体会从具体到抽象的认识过程,发展符号意识。
【学习重难点】
学习重点:理解字母表示数的意义,正确分析实际问题中的数量关系,并用含有字母的式子表示数量关系,感受其中“抽象”的数学思想。
学习难点:把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来。
【学习过程】
一、自主学习
1.议一议:列车在冻土地段行驶2小时的路程是多少千米?3小时又是多少千米?t小时呢?(说明:在含有字母的式子中如果出现乘号,通常将乘号写作“·”或省略不写。例如:100×t可以写成100·t或100t)
2.回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
二、合作探究
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是acm,高是hcm,用式子表示它的体积;
(4)用式子表示数n的相反数。
三、精讲释疑
(1)一条河的水流速度是2.5km/h,船在静水中的速度是vkm/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
(3)如图(1)(图中长度单位:cm),用式子表示三角尺的面积;
(4)如图(2)是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积。
四、当堂检测
1.关于多项式,下列说法正确的是( ).
A.次数是3 B.常数项是1 C.次数是5 D.三次项是
2.用表示的数一定是( )
A.正数 B.正数或负数 C.正整数 D.以上全不对
3.如图所示,边长为a的正方形中阴影部分的周长为( )
A.a2-πa2 B.a2-πa2
C.2a+πa D.2a+2πa
4.下列说法中正确的有( )个.
①的系数是7;②与没有系数;③的次数是5;
④的系数是;⑤的次数是;⑥的系数是.
A.0 B.1 C.2 D.3
5.将全体正偶数排成一个三角形数阵:
按照以上排列的规律,第10行第5个数是( )
A.98 B.100 C.102 D.104
6.篮球队要购买10个篮球,每个篮球元,一共需要__________元.(用含的代数式表示)
7.观察下列等式:,,,…按此规律,则第个等式为__________________.
8.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形中共有________个〇.
9.某花卉基地购买了一批水培植物营养液,已知甲种营养液每瓶2L,乙种营养液每瓶3L.
(1)若花卉基地购买了甲种营养液m箱(每箱12瓶),乙种营养液n箱(每箱10瓶),共QL.用含m,n的式子表示Q;
(2)若购进甲种营养液瓶,乙种营养液瓶,用科学记数法表示Q.
10.【做一做】列代数式
(1)已知一个三位数的个位数字是a,十位数字是b,百位数字是c,则这个三位数可表示为 ;
(2)某地区夏季高山的温度从山脚处开始每升高100米,降低0.7℃,若山脚温度是28℃,则比山脚高x米处的温度为 ℃;
(3)已知某礼堂第1排有18个座位,往后每一排比前一排多2个座位.则第n排共有座位数 个.
【数学思考】
(4)上面所列的代数式都属于我们所学习的整式中的 ;
(5)请你任意写一个关于x的这种类型的数字系数的二次式 ;
(6)用字母表示系数,写一个关于x的二次三项式,并注明字母系数应满足的条件 ;
【问题解决】
(7)若代数式3x|m|﹣(m﹣2)x+4是一个关于x的二次三项式,求m的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.D
3.C
4.B
5.B
6.
7..
8.6055
9.(1)
(2)
10(1)100c+10b+c;(2)(﹣0.007x+28);(3)(2n+16);(4)多项式;(5) x2+1;(6)ax2+bx+c(a、b、c均不为0);(7)-2.
7 / 7
