2022-2023学年沪教版(上海)六年级数学第一学期4.1圆的周长 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年沪教版(上海)六年级数学第一学期4.1圆的周长 课件(共20张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 10:57:06 | ||
图片预览





文档简介
(共20张PPT)
4.1 圆的周长
圆
同学们,你还记得圆的有关知识吗?
如图所示
半径OA
直径BC
一个圆的直径是它的半径的两倍,
反之,一个圆的半径是其直径的一半
A
O
B
.
情境引入
圆心O
C
圆的认识
1、圆心
圆心o
画圆时固定的那点就是圆心,用字母“O”表示,确定圆的位置。
半径r
2、半径
联结圆心和圆上任意一点的线段是圆的半径,用字母“r”表示,确定圆的大小。
直径d
3、直径
联结圆上任意两点且经过圆心的线段是圆的直径,用字母“d”表示。
d=2r
3米
3米
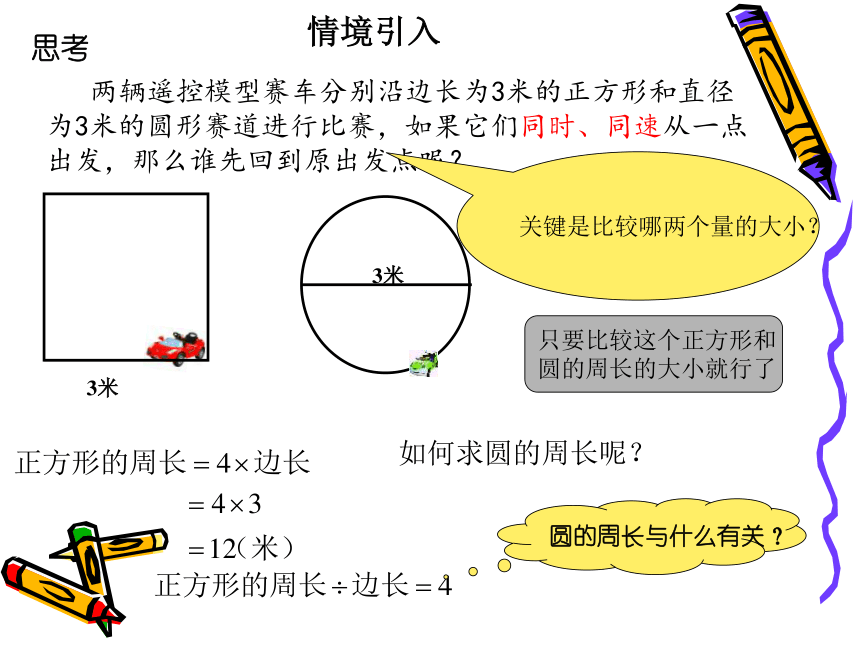
两辆遥控模型赛车分别沿边长为3米的正方形和直径为3米的圆形赛道进行比赛,如果它们同时、同速从一点出发,那么谁先回到原出发点呢?
情境引入
思考
关键是比较哪两个量的大小?
只要比较这个正方形和
圆的周长的大小就行了
如何求圆的周长呢?
圆的周长与什么有关?
新知讲授
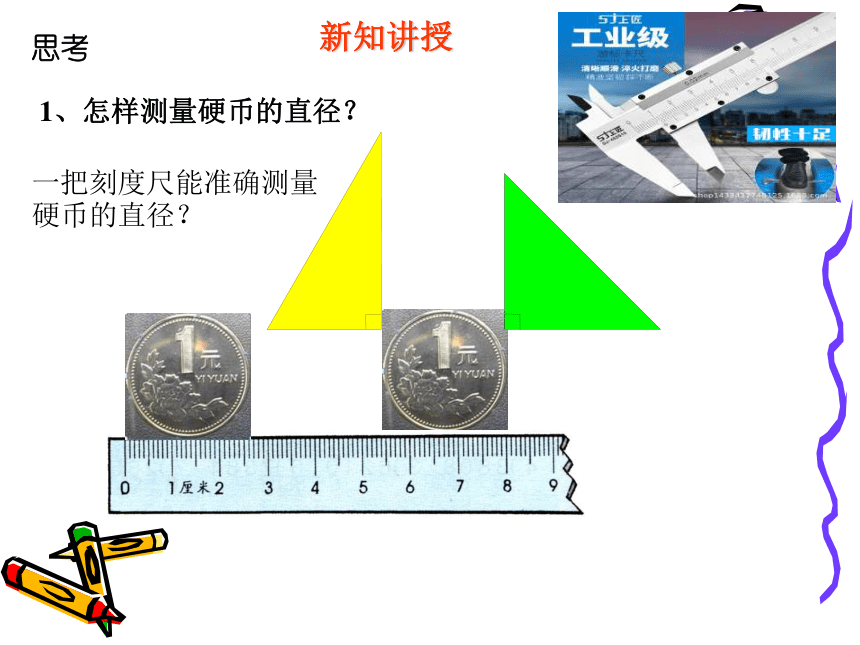
1、怎样测量硬币的直径?
思考
一把刻度尺能准确测量硬币的直径?
0
1
2
3
4
6
7
8
5
滚动法
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
新知讲授
思考
2、怎样测量硬币的周长?
0
1
2
3
4
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
化曲为直
操作
直径d (cm) 周长C (cm) C与d的比值
(保留两位小数)
五角硬币
一元硬币
新知讲授
通过测量硬币的直径和周长,把数据填入下表,计算周长和直径的比值(得数保留两位小数)
2
2.5
7.8
6.4
3.20
3.12
圆的周长都是直径的3倍多一些。
圆周率
刘徽 中国魏晋时期的杰出的数学家,中国古代数学理论奠基者之一,在详细整理我国古代数学名著《九章算术》时,他采取了把正多边形的边数逐渐增加去逼近圆周(也称割圆术)的方法,求得圆周率的近似值3.1416,这是当时世界上精确度最高的近似值。
新知讲授
祖冲之 两百多年后,南北朝的杰出数学家祖冲之,用简单地计算工具笔、尺等,将圆周率算到了小数点后面的第七位3.1415926,这在当时是件非常不容易的事。这个结论比西方数学家早了一千多年。
圆周率 是一个无限不循环小数,近似等于3.14,即π 3.14
*本章中,无特殊说明时,π取3.14, 将计算结果精确到0.01
C = πd
C = 2πr
新知讲授
概括
或
例1 一张王莲的叶子近似于一个圆,它的直径长约是0.95米。这张叶子的周长是多少米 (结果保留两位小数)
例题讲授
例题2 一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
例题讲授
6400
500
例题2 一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
6400
500
例题讲授
例3 如图,如果圆环的外圆周长 C1=250cm,内圆周长C2=150cm,求圆环的宽度d(结果精确到0.1cm)。
例题讲授
分析
d
O
R1
R2
已知外圆和内圆的周长
可求外圆半径R1和内圆半径R2
圆环的宽度d=R1-R2
例3 如图,如果圆环的外圆周长 C1=250cm,内圆周长C2=150cm,求圆环的宽度d(结果精确到0.1cm)。
d
O
R1
R2
例题讲授
C = πd
C = 2πr
课堂小结
或
4.1 圆的周长
圆
同学们,你还记得圆的有关知识吗?
如图所示
半径OA
直径BC
一个圆的直径是它的半径的两倍,
反之,一个圆的半径是其直径的一半
A
O
B
.
情境引入
圆心O
C
圆的认识
1、圆心
圆心o
画圆时固定的那点就是圆心,用字母“O”表示,确定圆的位置。
半径r
2、半径
联结圆心和圆上任意一点的线段是圆的半径,用字母“r”表示,确定圆的大小。
直径d
3、直径
联结圆上任意两点且经过圆心的线段是圆的直径,用字母“d”表示。
d=2r
3米
3米
两辆遥控模型赛车分别沿边长为3米的正方形和直径为3米的圆形赛道进行比赛,如果它们同时、同速从一点出发,那么谁先回到原出发点呢?
情境引入
思考
关键是比较哪两个量的大小?
只要比较这个正方形和
圆的周长的大小就行了
如何求圆的周长呢?
圆的周长与什么有关?
新知讲授
1、怎样测量硬币的直径?
思考
一把刻度尺能准确测量硬币的直径?
0
1
2
3
4
6
7
8
5
滚动法
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
新知讲授
思考
2、怎样测量硬币的周长?
0
1
2
3
4
新知讲授
思考
2、怎样测量硬币的周长?
绕线法
化曲为直
操作
直径d (cm) 周长C (cm) C与d的比值
(保留两位小数)
五角硬币
一元硬币
新知讲授
通过测量硬币的直径和周长,把数据填入下表,计算周长和直径的比值(得数保留两位小数)
2
2.5
7.8
6.4
3.20
3.12
圆的周长都是直径的3倍多一些。
圆周率
刘徽 中国魏晋时期的杰出的数学家,中国古代数学理论奠基者之一,在详细整理我国古代数学名著《九章算术》时,他采取了把正多边形的边数逐渐增加去逼近圆周(也称割圆术)的方法,求得圆周率的近似值3.1416,这是当时世界上精确度最高的近似值。
新知讲授
祖冲之 两百多年后,南北朝的杰出数学家祖冲之,用简单地计算工具笔、尺等,将圆周率算到了小数点后面的第七位3.1415926,这在当时是件非常不容易的事。这个结论比西方数学家早了一千多年。
圆周率 是一个无限不循环小数,近似等于3.14,即π 3.14
*本章中,无特殊说明时,π取3.14, 将计算结果精确到0.01
C = πd
C = 2πr
新知讲授
概括
或
例1 一张王莲的叶子近似于一个圆,它的直径长约是0.95米。这张叶子的周长是多少米 (结果保留两位小数)
例题讲授
例题2 一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
例题讲授
6400
500
例题2 一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
6400
500
例题讲授
例3 如图,如果圆环的外圆周长 C1=250cm,内圆周长C2=150cm,求圆环的宽度d(结果精确到0.1cm)。
例题讲授
分析
d
O
R1
R2
已知外圆和内圆的周长
可求外圆半径R1和内圆半径R2
圆环的宽度d=R1-R2
例3 如图,如果圆环的外圆周长 C1=250cm,内圆周长C2=150cm,求圆环的宽度d(结果精确到0.1cm)。
d
O
R1
R2
例题讲授
C = πd
C = 2πr
课堂小结
或
