7.6余角和补角课件 2022-2023学年沪教版(上海)六年级数学第二学期(共26张PPT)
文档属性
| 名称 | 7.6余角和补角课件 2022-2023学年沪教版(上海)六年级数学第二学期(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
7.6 余角和补角
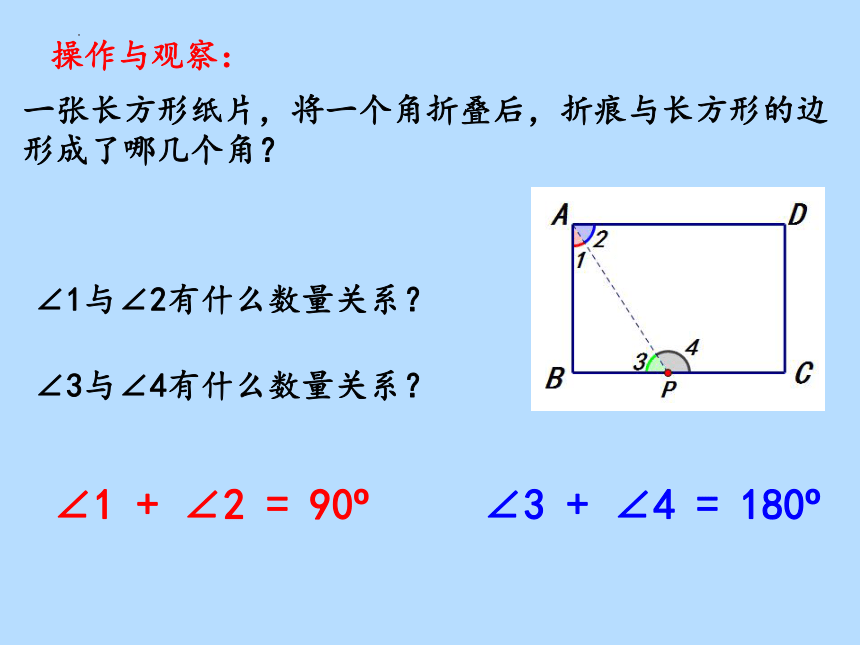
一张长方形纸片,将一个角折叠后,折痕与长方形的边形成了哪几个角?
操作与观察:
∠1与∠2有什么数量关系?
∠3与∠4有什么数量关系?
∠1 + ∠2 = 90
∠3 + ∠4 = 180
1
2
∠1是∠2的余角
∠2是∠1的余角
1.互为余角:
概念辨析:
如果两个角的度数的和是90 ,那么这两个角叫做互为余角,简称互余.其中一个角称为另一个角的余角.
∠1与∠2互余
用符号语言表示为:∠1 + ∠2 = 90
注:两角是否互余只跟这两角的大小有关,
与位置无关.
辨一辨
(2) 若∠A+∠B=90 ,则∠A是余角.( )
(1) 钝角没有余角. ( )
(3) 若∠1+∠2=90 ,但∠1和∠2不相邻,
则∠1和∠2不互余. ( )
若两锐角的和是90 ,则这两角互余.
√
×
×
O
1
2
概念辨析:
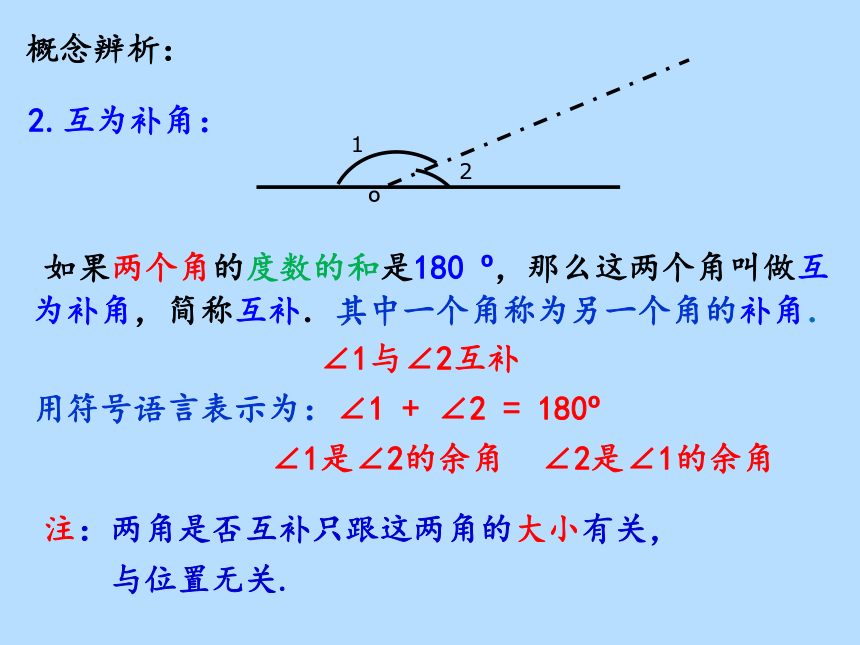
2.互为补角:
如果两个角的度数的和是180 ,那么这两个角叫做互为补角,简称互补.其中一个角称为另一个角的补角.
∠1与∠2互补
用符号语言表示为:∠1 + ∠2 = 180
∠1是∠2的余角
∠2是∠1的余角
注:两角是否互补只跟这两角的大小有关,
与位置无关.
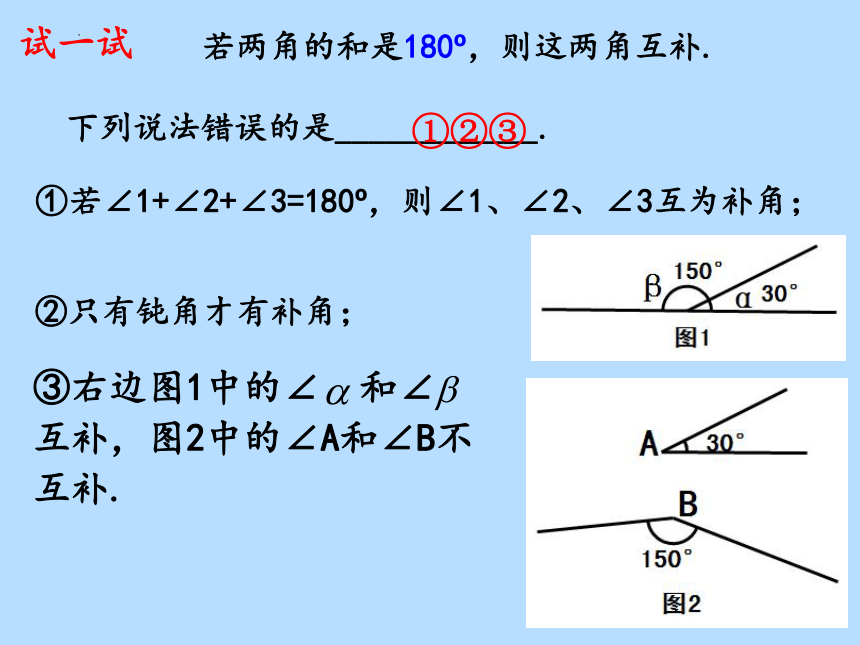
试一试
①若∠1+∠2+∠3=180 ,则∠1、∠2、∠3互为补角;
下列说法错误的是____________.
若两角的和是180 ,则这两角互补.
②只有钝角才有补角;
③右边图1中的∠ 和∠
互补,图2中的∠A和∠B不互补.
①②③
A
B
C
D
O
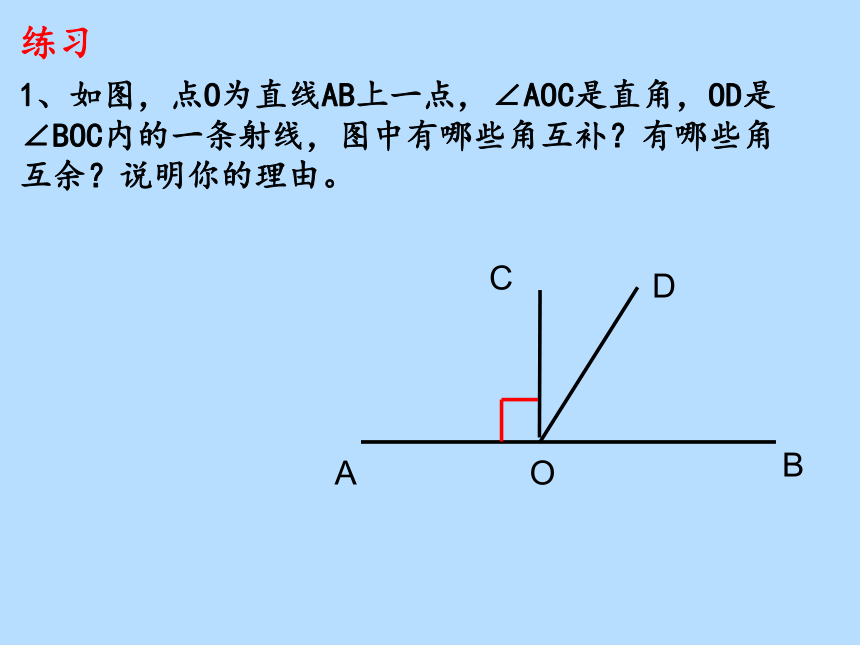
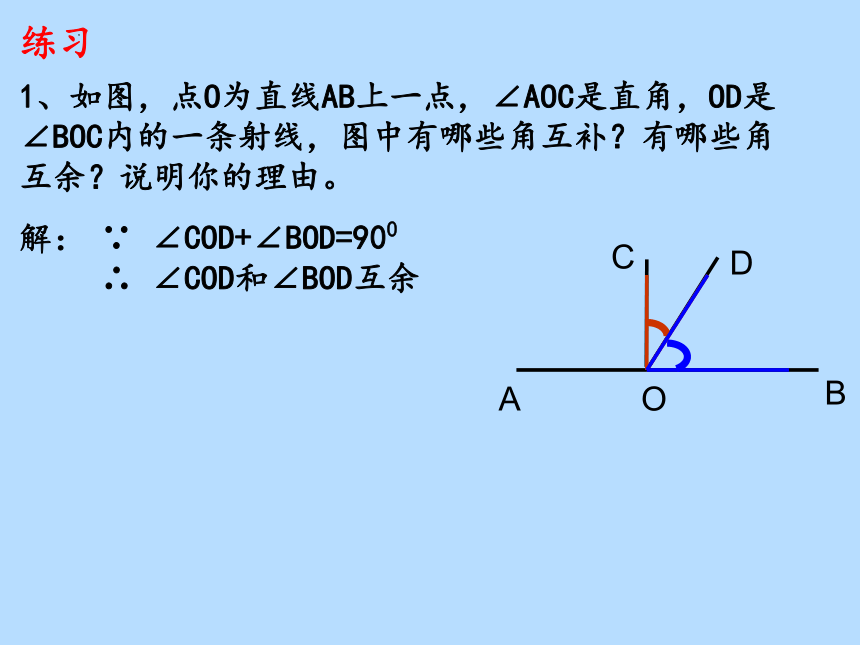
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
练习
A
B
C
D
O
∵ ∠COD+∠BOD=900
∴ ∠COD和∠BOD互余
练习
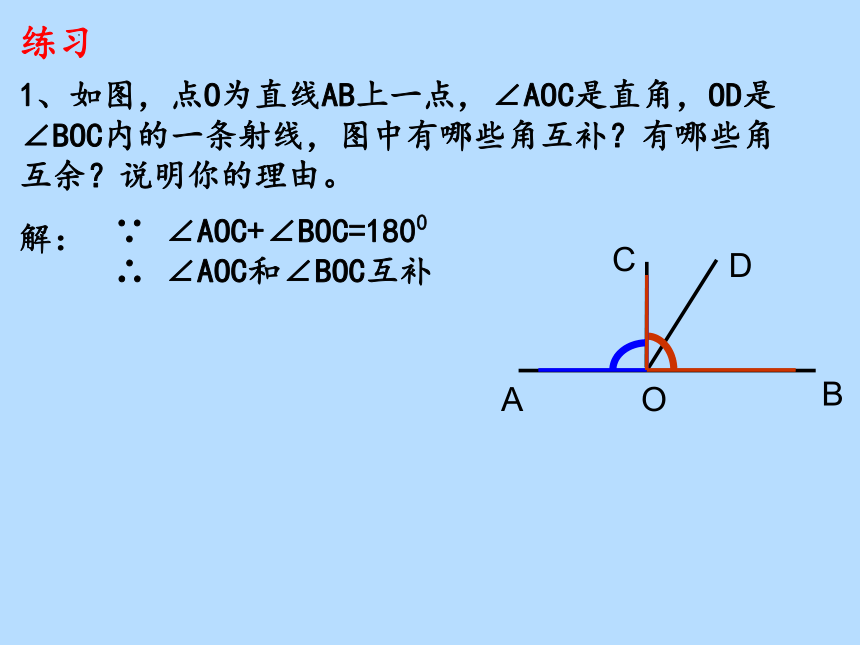
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
解:
A
B
C
D
O
∵ ∠AOC+∠BOC=1800
∴ ∠AOC和∠BOC互补
解:
练习
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
A
B
C
D
O
∵ ∠AOD+∠BOD=1800
∴ ∠AOD和∠BOD互补
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
解:
练习
练习2:(1)填空
的余角 的补角
30°
45°
76°
x°
60°
150°
45°
135°
90°-x°
180°-x°
14°
104°
从这张表格中,比较同一个锐角的余角
和补角的度数,你能发现什么规律?
同一个锐角的补角比它的余角大90度
练习2:(2)回答下列问题
(1)一个角与它的余角相等,这个角的度数是多少?
(2)一个角与它的补角相等,这个角的度数是多少?
(3)互补的两个角能否都是锐角?能否都是直角?能否都是钝角?
例1、已知一个角的补角是这个角的余角的3倍,求这个角的度数。
解:设这个角为x0
180-x=270-3x
2x=90
x=45
答:这个角为450
180-x=3(90-x)
练习 已知一个角的补角比它的余角的2倍大350,求这个角的度数.
在研究角的度量时,往往需要比度更小的单位,
90°=89°60 ′
(二)角的度量单位
角的度量单位度、分、秒的关系
比如说
180°=179°60 ′
把1度的角分成60等份,那么每1份就是1分,记作1′;
分:
秒:
1分 记作:1′
1秒 记作:1"
再把1分的角分成60等份,每1份就是1秒,记作1″
1°=60′
1′=60"
练习3:计算
(2)89°6′4″-24°27 ′35″
(1)77°54 ′36″+34°27 ′44″
例题2 已知 =53°38′,求 的余角与补角的度数.
解: 的余角=90°- 53°38′
=126°22′
=36°22′
的补角=180°- 53°38′
1
2
3
思考:∠2和∠3相等吗?为什么
1、画出∠1的余角
相等
∵ ∠2是∠1的余角
∴ ∠2=900- ∠1
∵ ∠3是∠1的余角
∴ ∠3=900- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的余角,∠2和∠3相等,
“同角的余角相等。”
性质学习:
1
2
3
2、画出∠1的补角
思考:∠2和∠3相等吗?为什么
相等
∵ ∠2是∠1的补角
∴ ∠2=1800- ∠1
∵ ∠3是∠1的补角
∴ ∠3=1800- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的补角,∠2和∠3相等,
“同角的补角相等。”
性质学习:
同角(等角)的余角相等.
同角(等角)的补角相等.
符号语言:
∵∠1 + ∠2 = 90°
∠1 + ∠3 = 90°
∴∠2 =∠3(同角的余角相等)
符号语言:
∵∠1 + ∠2 = 180°
∠1 + ∠3 = 180°
∴∠2 =∠3(同角的补角相等)
归纳性质:
练习4:如图,一幅三角板如图所示,已知∠1=40 ,∠2=__________ .
练习5:如图,直线CD经过点O,且OC平分∠AOB.
试判断∠AOD与∠BOD的大小关系,并说明理由.
O
D
A
B
C
答:∠AOD=∠BOD
又∵∠AOD + ∠AOC =180
∠BOD + ∠BOC =180
∵OC平分∠AOB
∴∠AOD=∠BOD
(等角的补角相等)
∴∠AOC =∠BOC
课堂小结:
互为余角(互余) 互为补角(互补)
定义
性质
注意
如果两个角的度数和是90 ,我们就说这两个角互为余角,简称互余.
如果两个角的度数和是180 ,我们就说这两个角互为补角,简称互补.
同角(等角)的余角相等
同角(等角)的补角相等
①互余、互补都是指两个角;
②互余、互补只与两角和有关,
与角的位置无关.
拓展
1、如图,M、N分别是线段AB、BC的中点,AC=10,求MN的长。
A
C
N
M
B
拓展
变式、如图,M、N分别是线段AB、BC的中点,MN=8,求AC的长。
A
C
N
M
B
2、如图,OP、OQ分别平分∠AOB、∠BOC,若∠AOC=130°求∠POQ的度数.
Q
O
B
C
P
A
拓展
变式、如图,OP、OQ分别平分∠AOB、∠BOC,若∠POQ=60°求∠AOC的度数.
Q
O
B
C
P
A
拓展
7.6 余角和补角
一张长方形纸片,将一个角折叠后,折痕与长方形的边形成了哪几个角?
操作与观察:
∠1与∠2有什么数量关系?
∠3与∠4有什么数量关系?
∠1 + ∠2 = 90
∠3 + ∠4 = 180
1
2
∠1是∠2的余角
∠2是∠1的余角
1.互为余角:
概念辨析:
如果两个角的度数的和是90 ,那么这两个角叫做互为余角,简称互余.其中一个角称为另一个角的余角.
∠1与∠2互余
用符号语言表示为:∠1 + ∠2 = 90
注:两角是否互余只跟这两角的大小有关,
与位置无关.
辨一辨
(2) 若∠A+∠B=90 ,则∠A是余角.( )
(1) 钝角没有余角. ( )
(3) 若∠1+∠2=90 ,但∠1和∠2不相邻,
则∠1和∠2不互余. ( )
若两锐角的和是90 ,则这两角互余.
√
×
×
O
1
2
概念辨析:
2.互为补角:
如果两个角的度数的和是180 ,那么这两个角叫做互为补角,简称互补.其中一个角称为另一个角的补角.
∠1与∠2互补
用符号语言表示为:∠1 + ∠2 = 180
∠1是∠2的余角
∠2是∠1的余角
注:两角是否互补只跟这两角的大小有关,
与位置无关.
试一试
①若∠1+∠2+∠3=180 ,则∠1、∠2、∠3互为补角;
下列说法错误的是____________.
若两角的和是180 ,则这两角互补.
②只有钝角才有补角;
③右边图1中的∠ 和∠
互补,图2中的∠A和∠B不互补.
①②③
A
B
C
D
O
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
练习
A
B
C
D
O
∵ ∠COD+∠BOD=900
∴ ∠COD和∠BOD互余
练习
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
解:
A
B
C
D
O
∵ ∠AOC+∠BOC=1800
∴ ∠AOC和∠BOC互补
解:
练习
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
A
B
C
D
O
∵ ∠AOD+∠BOD=1800
∴ ∠AOD和∠BOD互补
1、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
解:
练习
练习2:(1)填空
的余角 的补角
30°
45°
76°
x°
60°
150°
45°
135°
90°-x°
180°-x°
14°
104°
从这张表格中,比较同一个锐角的余角
和补角的度数,你能发现什么规律?
同一个锐角的补角比它的余角大90度
练习2:(2)回答下列问题
(1)一个角与它的余角相等,这个角的度数是多少?
(2)一个角与它的补角相等,这个角的度数是多少?
(3)互补的两个角能否都是锐角?能否都是直角?能否都是钝角?
例1、已知一个角的补角是这个角的余角的3倍,求这个角的度数。
解:设这个角为x0
180-x=270-3x
2x=90
x=45
答:这个角为450
180-x=3(90-x)
练习 已知一个角的补角比它的余角的2倍大350,求这个角的度数.
在研究角的度量时,往往需要比度更小的单位,
90°=89°60 ′
(二)角的度量单位
角的度量单位度、分、秒的关系
比如说
180°=179°60 ′
把1度的角分成60等份,那么每1份就是1分,记作1′;
分:
秒:
1分 记作:1′
1秒 记作:1"
再把1分的角分成60等份,每1份就是1秒,记作1″
1°=60′
1′=60"
练习3:计算
(2)89°6′4″-24°27 ′35″
(1)77°54 ′36″+34°27 ′44″
例题2 已知 =53°38′,求 的余角与补角的度数.
解: 的余角=90°- 53°38′
=126°22′
=36°22′
的补角=180°- 53°38′
1
2
3
思考:∠2和∠3相等吗?为什么
1、画出∠1的余角
相等
∵ ∠2是∠1的余角
∴ ∠2=900- ∠1
∵ ∠3是∠1的余角
∴ ∠3=900- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的余角,∠2和∠3相等,
“同角的余角相等。”
性质学习:
1
2
3
2、画出∠1的补角
思考:∠2和∠3相等吗?为什么
相等
∵ ∠2是∠1的补角
∴ ∠2=1800- ∠1
∵ ∠3是∠1的补角
∴ ∠3=1800- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的补角,∠2和∠3相等,
“同角的补角相等。”
性质学习:
同角(等角)的余角相等.
同角(等角)的补角相等.
符号语言:
∵∠1 + ∠2 = 90°
∠1 + ∠3 = 90°
∴∠2 =∠3(同角的余角相等)
符号语言:
∵∠1 + ∠2 = 180°
∠1 + ∠3 = 180°
∴∠2 =∠3(同角的补角相等)
归纳性质:
练习4:如图,一幅三角板如图所示,已知∠1=40 ,∠2=__________ .
练习5:如图,直线CD经过点O,且OC平分∠AOB.
试判断∠AOD与∠BOD的大小关系,并说明理由.
O
D
A
B
C
答:∠AOD=∠BOD
又∵∠AOD + ∠AOC =180
∠BOD + ∠BOC =180
∵OC平分∠AOB
∴∠AOD=∠BOD
(等角的补角相等)
∴∠AOC =∠BOC
课堂小结:
互为余角(互余) 互为补角(互补)
定义
性质
注意
如果两个角的度数和是90 ,我们就说这两个角互为余角,简称互余.
如果两个角的度数和是180 ,我们就说这两个角互为补角,简称互补.
同角(等角)的余角相等
同角(等角)的补角相等
①互余、互补都是指两个角;
②互余、互补只与两角和有关,
与角的位置无关.
拓展
1、如图,M、N分别是线段AB、BC的中点,AC=10,求MN的长。
A
C
N
M
B
拓展
变式、如图,M、N分别是线段AB、BC的中点,MN=8,求AC的长。
A
C
N
M
B
2、如图,OP、OQ分别平分∠AOB、∠BOC,若∠AOC=130°求∠POQ的度数.
Q
O
B
C
P
A
拓展
变式、如图,OP、OQ分别平分∠AOB、∠BOC,若∠POQ=60°求∠AOC的度数.
Q
O
B
C
P
A
拓展
