北师大版(2019)必修第一册第五章函数的应用 综合拔高练(Word版含解析)
文档属性
| 名称 | 北师大版(2019)必修第一册第五章函数的应用 综合拔高练(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 11:25:19 | ||
图片预览




文档简介
第五章 函数应用
综合拔高练
五年高考练
考点1 函数零点、方程的根与函数图象的关系
1.(2020全国Ⅰ理,12)若2a+log2a=4b+2log4b,则( )
A.a>2b B.a<2b C.a>b2 D.a2.(2020天津,9)已知函数f(x)=若函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,则k的取值范围是( )
A.∪(2,+∞)
B.∪(0,2)
C.(-∞,0)∪(0,2)
D.(-∞,0)∪(2,+∞)
3.(2018课标全国Ⅰ,9)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
4.(2017课标全国Ⅲ,12)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )
A.- B. C. D.1
5.(2021北京,15)已知f(x)=|lg x|-kx-2,给出下列四个结论:
(1)若k=0,则f(x)有两个零点;
(2) k<0,使得f(x)有一个零点;
(3) k<0,使得f(x)有三个零点;
(4) k>0,使得f(x)有三个零点.
以上正确结论的序号是 .
6.(2018浙江,15)已知λ∈R,函数f(x)=当λ=2时,不等式f(x)<0的解集是 .若函数f(x)恰有2个零点,则λ的取值范围是 .
7.(2018天津,14)已知a>0,函数f(x)=若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是 .
考点2 函数模型的应用
8.(2020全国新高考Ⅰ,6)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)( )
A.1.2天 B.1.8天 C.2.5天 D.3.5天
9.(2020全国Ⅲ理,4)Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63 C.66 D.69
三年模拟练
应用实践
1.(2021江西抚州期末)用二分法求函数f(x)=log2x+a-2x零点的近似值时,如果确定零点所处的初始区间为,那么a的取值范围为( )
A.(-∞,2)
B.
C.
D.(-∞,2)∪
2.(2020山东日照期中)函数f(x)=-的零点所在的区间为( )
A. B.
C. D.
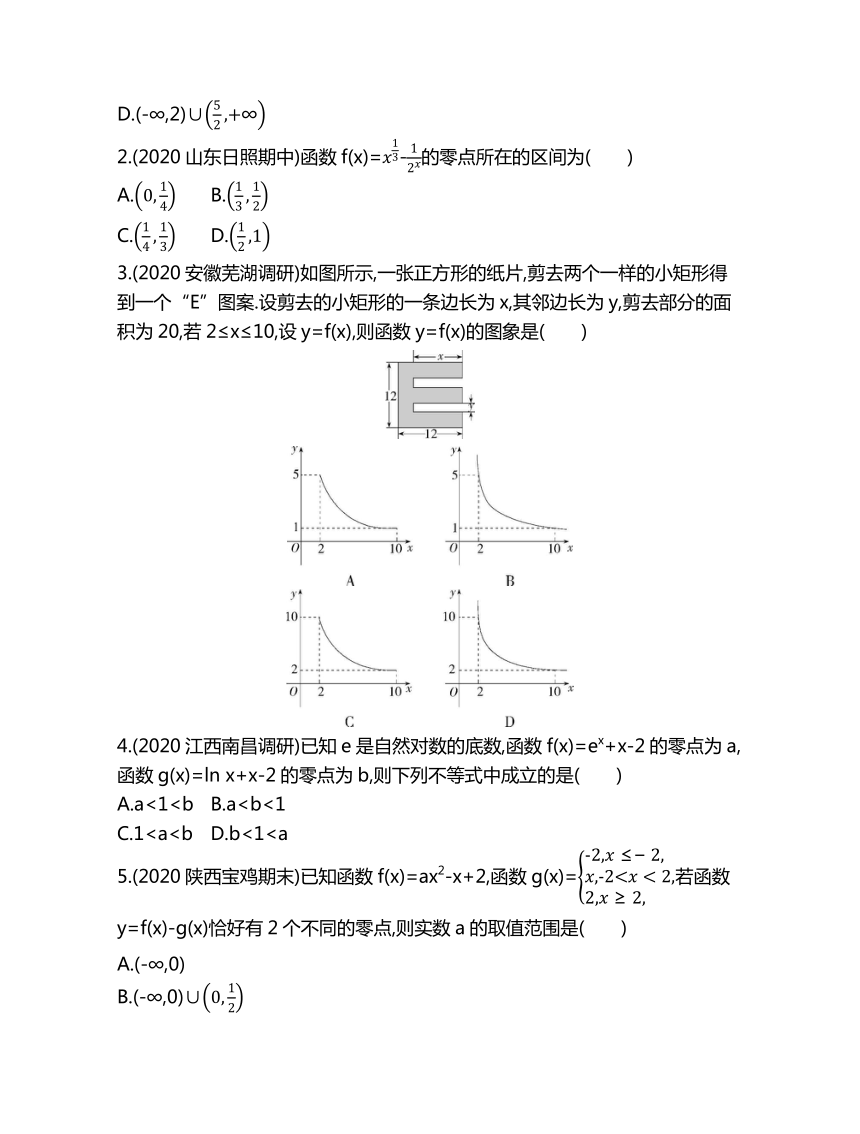
3.(2020安徽芜湖调研)如图所示,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案.设剪去的小矩形的一条边长为x,其邻边长为y,剪去部分的面积为20,若2≤x≤10,设y=f(x),则函数y=f(x)的图象是( )
4.(2020江西南昌调研)已知e是自然对数的底数,函数f(x)=ex+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,则下列不等式中成立的是( )
A.a<1C.15.(2020陕西宝鸡期末)已知函数f(x)=ax2-x+2,函数g(x)=若函数y=f(x)-g(x)恰好有2个不同的零点,则实数a的取值范围是( )
A.(-∞,0)
B.(-∞,0)∪
C.(-∞,0)∪
D.(-∞,0)∪(1,+∞)
6.(2022广西柳州一模)5G技术的数学原理之一是著名的香农公式:C=Wlog2,它表示在受高斯白噪声干扰的信道中,最大信息传递速率C取决于信道带宽W.S是信道内所传信号的平均功率,N是信道内部的高斯噪声功率,叫作信噪比.按照香农公式,在不改变W的情况下,将信噪比从1 999提升至λ,使得C增加了20%,则λ的值约为(参考数据:lg 2≈0.3,103.96≈9 120)( )
A.9 121 B.9 119
C.9 919 D.10 999
7.(2022北京一零一中学期末)已知某种药物在血液中以每小时20%的比例衰减,现给某病人静脉注射了该药物2 500 mg,设经过x小时后,药物在病人血液中的量为y mg.
(1)y与x的关系式为 ;
(2)当该药物在病人血液中的量保持在1 500 mg以上时,才有疗效;而低于500 mg时,病人就有危险,则要使病人没有危险,再次注射该药物的时间不能超过 小时.(参考数据:0.82.3≈0.6,0.87.2≈0.2,0.89.9≈0.11)
8.(2020福建龙岩一中月考)已知函数f(x)=x2-3mx+n的两个零点分别为1和2.
(1)求m,n的值;
(2)若不等式f(x)-k>0在x∈[0,5]上恒成立,求k的取值范围;
(3)令g(x)=,若函数F(x)=g(2x)-r·2x在x∈[-1,1]上有零点,求实数r的取值范围.
迁移创新
9.(2022山西太原期中)国庆节期间,某商场进行如下的优惠促销活动:
优惠一:一次购买商品的价格,每满60元立减5元;
优惠二:在优惠一之后,每满400元再减40元.
例如,一次购买商品的价格为140元,则实际支付金额为140-5×=140-5×2=130(元),其中[x]表示不大于x的最大整数.又如,一次购买商品的价格为880元,则实际支付金额为880-5×-40×2=730(元).
(1)小明计划在该商场购买两件价格分别是250元和650元的商品,他是分两次支付好,还是一次性支付好 请说明理由;
(2)已知某商品是小明常用必需品,其价格为30元/件.小明趁商场促销,想多购买几件该商品,其预算不超过500元,试求他应购买多少件该商品,才能使其平均价格最低.最低平均价格是多少
本章达标检测见增分测评卷 P9
答案与分层梯度式解析
第五章 函数应用
综合拔高练
五年高考练
1.B 2a+log2a=22b+log2b<22b+log2(2b),
令f(x)=2x+log2x,则f(a)易知f(x)在(0,+∞)上单调递增,
所以a<2b,故选B.
2.D 令h(x)=|kx2-2x|,函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,即y=f(x)与y=h(x)的图象恰有4个不同交点.
当k=-时,h(x)==,在同一直角坐标系中作出y=f(x),y=h(x)的图象,如图1所示.
此时y=f(x)与y=h(x)的图象恰有4个不同交点,即函数g(x)=f(x)-|kx2-2x|恰有4个零点,排除A,B;
当k=1时,h(x)=|x2-2x|,作出y=h(x)与y=f(x)的图象,如图2所示.
此时函数y=f(x)与y=h(x)的图象仅有2个交点,不符合题意,排除C.故选D.
3.C 令h(x)=-x-a,由题意可知函数f(x)与h(x)的图象存在2个交点,如图,
当x=0时,h(0)=-a,由图可知要满足y=f(x)与y=h(x)的图象存在2个交点,需要-a≤1,即a≥-1.故选C.
4.C 由函数f(x)有零点,得x2-2x+a(ex-1+e-x+1)=0有解,即(x-1)2-1+a(ex-1+e-x+1)=0有解,
令t=x-1,则上式可化为t2-1+a(et+e-t)=0,即a=.
令h(t)=,易得h(t)为偶函数,
由f(x)有唯一零点得函数h(t)的图象与直线y=a有唯一交点,则此交点的横坐标为0,
所以a==,故选C.
5.答案 (1)(2)(4)
解析 令f(x)=|lg x|-kx-2=0,得|lg x|=kx+2,
令g(x)=|lg x|,h(x)=kx+2,
所以f(x)的零点个数即函数g(x)与h(x)图象的交点个数.
当k=0时,如图a,g(x)与h(x)的图象有两个交点,则f(x)有两个零点,故(1)正确;
当k>0时,如图b,存在h(x)=k0x+2的图象与函数g(x)=|lg x|(x>1)的图象相切的情况,此时h(x)与g(x)的图象有两个交点,当0当k<0时,如图c,g(x)与h(x)的图象最多有两个交点,g(x)与h(x)的图象相切时有一个交点,如图d,故(2)正确,(3)不正确.
综上,正确结论的序号为(1)(2)(4).
图a
图b
图c
图d
6.答案 (1,4);(1,3]∪(4,+∞)
解析 当λ=2时,不等式f(x)<0等价于
或
即2≤x<4或1故不等式f(x)<0的解集为(1,4).
易知函数y=x-4(x∈R)有一个零点x1=4,函数y=x2-4x+3(x∈R)有两个零点x2=1,x3=3.
在同一坐标系中作出这两个函数的图象,要使函数f(x)恰有2个零点,则只能有以下两种情形:①两个零点为1,3,结合图可知,此时λ>4.②两个零点为1,4,结合图可知,此时1<λ≤3.
综上,λ的取值范围为(1,3]∪(4,+∞).
7.答案 (4,8)
解析 设g(x)=f(x)-ax,由题意可知方程f(x)=ax恰有2个互异的实数解即函数y=g(x)有2个零点,即y=g(x)的图象与x轴有2个交点,满足条件的y=g(x)的图象有以下两种情况:
情况一:
则∴4情况二:
则不等式组无解.
综上,满足条件的a的取值范围是(4,8).
8.B 因为R0=3.28,T=6且R0=1+rT,所以指数增长率r==0.38,设累计感染病例数增加1倍需要的时间为t天,则I(t)=2I(0),即ert=2,即e0.38t=2,两边取自然对数得ln e0.38t=ln 2,即0.38t=ln 2,又ln 2≈0.69,所以t=≈≈1.8.故选B.
9.C I(t*)==0.95K,整理可得=19,两边取自然对数得0.23(t*-53)=ln 19,解得t*≈66,故选C.
三年模拟练
1.C 若零点所处的初始区间为,
则f f =·(-1+a-1)<0,
解得22.B 易知f(x)在R上单调递增,其图象是一条连续的曲线.∵f =-<0,f =->0,
∴f(x)的零点所在的区间为.故选B.
3.A 由题意知2xy=20,∴xy=10,∴y=(2≤x≤10),故选A.
4.A 令f(x)=ex+x-2=0,则ex=2-x,
令g(x)=ln x+x-2=0,则ln x=2-x,
设y1=ex,y2=ln x,y3=2-x,
在同一平面直角坐标系中作出函数y1=ex,y2=ln x,y3=2-x的图象,如图.
∵函数f(x)=ex+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,
∴y1=ex与y3=2-x图象的交点的横坐标为a,y2=ln x与y3=2-x图象的交点的横坐标为b,由图象知a<15.B 依题意得f(x)与g(x)的图象有2个不同的交点,且f(x)的图象恒过点(0,2).
当a=0时, f(x)=2-x,此时f(x)与g(x)的图象仅有1个交点,舍去.
当a<0时, f(x)的图象开口向下且恒过点(0,2),此时f(x)与g(x)的图象一定有2个不同的交点.
当a>0时, f(x)的图象开口向上且恒过点(0,2),对称轴为直线x=,且>0.
当f(x)与g(x)的图象仅有1个交点时,可求得a=.
要使f(x)与g(x)的图象有2个不同的交点,只需0综上,实数a的取值范围是(-∞,0)∪.
故选B.
6.B 由题意得=20%,
∴=1.2,∴log2(1+λ)=1.2log22 000,
∴1+λ=2 0001.2,∴λ=2 0001.2-1,
又∵lg2 0001.2=1.2lg 2 000=1.2(lg 2+3)≈1.2×(0.3+3)=3.96,
∴2 0001.2=103.96≈9 120,∴λ=2 0001.2-1=9 119.
7.答案 (1)y=2 500×0.8x (2)7.2
解析 (1)由题意知,经过x小时后,药物在病人血液中的量y=2 500×(1-20%)x=2 500×0.8x,即y与x的关系式为y=2 500×0.8x.
(2)令2 500×0.8x≥500,即0.8x≥0.2.
∵0.87.2≈0.2,y=0.8x是单调递减函数,
∴x≤7.2,
∴要使病人没有危险,再次注射该药物的时间不能超过7.2小时.
8.解析 (1)由函数f(x)=x2-3mx+n的两个零点分别为1和2,
可得1-3m+n=0,4-6m+n=0,解得m=1,n=2.
(2)由(1)可得f(x)=x2-3x+2.
由不等式f(x)-k>0在x∈[0,5]上恒成立,可得不等式k∵f(x)=x2-3x+2=-,
∴f(x)=x2-3x+2在x∈[0,5]上的最小值为f =-,∴k<-.
(3)由(1)得g(x)==x+-3.
∵函数F(x)=g(2x)-r·2x在x∈[-1,1]上有零点,
∴g(2x)-r·2x=0在x∈[-1,1]上有解,即r=1+2·-3·在x∈[-1,1]上有解,
令t=,则t∈,
r=2t2-3t+1=2-,
∴-≤r≤3,
∴实数r的取值范围是.
9.解析 (1)一次性支付好.理由如下:
分两次支付时,支付金额为250-5×+650-5×-40=230+600-40=790(元).
一次性支付时,支付金额为250+650-5×-40×2=745(元).
因为745<790,所以一次性支付好.
(2)设购买x(x∈N+)件,平均价格为y元/件.
由于预算不超过500元,所以最多购买19件.
当1≤x≤14,x∈N+时,不能享受优惠二,
y==30-×
=
=
又27.5+>27.5,
所以当购买偶数件时,y取得最小值,且ymin=27.5.
当15≤x≤19,x∈N+时,能享受优惠二,
y==30-×-
=
=
若x为偶数,则x=16时,y取得最小值,且ymin=25.
若x为奇数,则y随n的增大而增大,所以当x=15时,y取得最小值,且ymin=25.
又25<27.5,所以购买15件或16件该商品,才能使其平均价格最低,最低平均价格为25元/件.
综合拔高练
五年高考练
考点1 函数零点、方程的根与函数图象的关系
1.(2020全国Ⅰ理,12)若2a+log2a=4b+2log4b,则( )
A.a>2b B.a<2b C.a>b2 D.a
A.∪(2,+∞)
B.∪(0,2)
C.(-∞,0)∪(0,2)
D.(-∞,0)∪(2,+∞)
3.(2018课标全国Ⅰ,9)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
4.(2017课标全国Ⅲ,12)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )
A.- B. C. D.1
5.(2021北京,15)已知f(x)=|lg x|-kx-2,给出下列四个结论:
(1)若k=0,则f(x)有两个零点;
(2) k<0,使得f(x)有一个零点;
(3) k<0,使得f(x)有三个零点;
(4) k>0,使得f(x)有三个零点.
以上正确结论的序号是 .
6.(2018浙江,15)已知λ∈R,函数f(x)=当λ=2时,不等式f(x)<0的解集是 .若函数f(x)恰有2个零点,则λ的取值范围是 .
7.(2018天津,14)已知a>0,函数f(x)=若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是 .
考点2 函数模型的应用
8.(2020全国新高考Ⅰ,6)基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)( )
A.1.2天 B.1.8天 C.2.5天 D.3.5天
9.(2020全国Ⅲ理,4)Logistic模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位:天)的Logistic模型:I(t)=,其中K为最大确诊病例数.当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3)( )
A.60 B.63 C.66 D.69
三年模拟练
应用实践
1.(2021江西抚州期末)用二分法求函数f(x)=log2x+a-2x零点的近似值时,如果确定零点所处的初始区间为,那么a的取值范围为( )
A.(-∞,2)
B.
C.
D.(-∞,2)∪
2.(2020山东日照期中)函数f(x)=-的零点所在的区间为( )
A. B.
C. D.
3.(2020安徽芜湖调研)如图所示,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案.设剪去的小矩形的一条边长为x,其邻边长为y,剪去部分的面积为20,若2≤x≤10,设y=f(x),则函数y=f(x)的图象是( )
4.(2020江西南昌调研)已知e是自然对数的底数,函数f(x)=ex+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,则下列不等式中成立的是( )
A.a<1C.1
A.(-∞,0)
B.(-∞,0)∪
C.(-∞,0)∪
D.(-∞,0)∪(1,+∞)
6.(2022广西柳州一模)5G技术的数学原理之一是著名的香农公式:C=Wlog2,它表示在受高斯白噪声干扰的信道中,最大信息传递速率C取决于信道带宽W.S是信道内所传信号的平均功率,N是信道内部的高斯噪声功率,叫作信噪比.按照香农公式,在不改变W的情况下,将信噪比从1 999提升至λ,使得C增加了20%,则λ的值约为(参考数据:lg 2≈0.3,103.96≈9 120)( )
A.9 121 B.9 119
C.9 919 D.10 999
7.(2022北京一零一中学期末)已知某种药物在血液中以每小时20%的比例衰减,现给某病人静脉注射了该药物2 500 mg,设经过x小时后,药物在病人血液中的量为y mg.
(1)y与x的关系式为 ;
(2)当该药物在病人血液中的量保持在1 500 mg以上时,才有疗效;而低于500 mg时,病人就有危险,则要使病人没有危险,再次注射该药物的时间不能超过 小时.(参考数据:0.82.3≈0.6,0.87.2≈0.2,0.89.9≈0.11)
8.(2020福建龙岩一中月考)已知函数f(x)=x2-3mx+n的两个零点分别为1和2.
(1)求m,n的值;
(2)若不等式f(x)-k>0在x∈[0,5]上恒成立,求k的取值范围;
(3)令g(x)=,若函数F(x)=g(2x)-r·2x在x∈[-1,1]上有零点,求实数r的取值范围.
迁移创新
9.(2022山西太原期中)国庆节期间,某商场进行如下的优惠促销活动:
优惠一:一次购买商品的价格,每满60元立减5元;
优惠二:在优惠一之后,每满400元再减40元.
例如,一次购买商品的价格为140元,则实际支付金额为140-5×=140-5×2=130(元),其中[x]表示不大于x的最大整数.又如,一次购买商品的价格为880元,则实际支付金额为880-5×-40×2=730(元).
(1)小明计划在该商场购买两件价格分别是250元和650元的商品,他是分两次支付好,还是一次性支付好 请说明理由;
(2)已知某商品是小明常用必需品,其价格为30元/件.小明趁商场促销,想多购买几件该商品,其预算不超过500元,试求他应购买多少件该商品,才能使其平均价格最低.最低平均价格是多少
本章达标检测见增分测评卷 P9
答案与分层梯度式解析
第五章 函数应用
综合拔高练
五年高考练
1.B 2a+log2a=22b+log2b<22b+log2(2b),
令f(x)=2x+log2x,则f(a)
所以a<2b,故选B.
2.D 令h(x)=|kx2-2x|,函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,即y=f(x)与y=h(x)的图象恰有4个不同交点.
当k=-时,h(x)==,在同一直角坐标系中作出y=f(x),y=h(x)的图象,如图1所示.
此时y=f(x)与y=h(x)的图象恰有4个不同交点,即函数g(x)=f(x)-|kx2-2x|恰有4个零点,排除A,B;
当k=1时,h(x)=|x2-2x|,作出y=h(x)与y=f(x)的图象,如图2所示.
此时函数y=f(x)与y=h(x)的图象仅有2个交点,不符合题意,排除C.故选D.
3.C 令h(x)=-x-a,由题意可知函数f(x)与h(x)的图象存在2个交点,如图,
当x=0时,h(0)=-a,由图可知要满足y=f(x)与y=h(x)的图象存在2个交点,需要-a≤1,即a≥-1.故选C.
4.C 由函数f(x)有零点,得x2-2x+a(ex-1+e-x+1)=0有解,即(x-1)2-1+a(ex-1+e-x+1)=0有解,
令t=x-1,则上式可化为t2-1+a(et+e-t)=0,即a=.
令h(t)=,易得h(t)为偶函数,
由f(x)有唯一零点得函数h(t)的图象与直线y=a有唯一交点,则此交点的横坐标为0,
所以a==,故选C.
5.答案 (1)(2)(4)
解析 令f(x)=|lg x|-kx-2=0,得|lg x|=kx+2,
令g(x)=|lg x|,h(x)=kx+2,
所以f(x)的零点个数即函数g(x)与h(x)图象的交点个数.
当k=0时,如图a,g(x)与h(x)的图象有两个交点,则f(x)有两个零点,故(1)正确;
当k>0时,如图b,存在h(x)=k0x+2的图象与函数g(x)=|lg x|(x>1)的图象相切的情况,此时h(x)与g(x)的图象有两个交点,当0
综上,正确结论的序号为(1)(2)(4).
图a
图b
图c
图d
6.答案 (1,4);(1,3]∪(4,+∞)
解析 当λ=2时,不等式f(x)<0等价于
或
即2≤x<4或1
易知函数y=x-4(x∈R)有一个零点x1=4,函数y=x2-4x+3(x∈R)有两个零点x2=1,x3=3.
在同一坐标系中作出这两个函数的图象,要使函数f(x)恰有2个零点,则只能有以下两种情形:①两个零点为1,3,结合图可知,此时λ>4.②两个零点为1,4,结合图可知,此时1<λ≤3.
综上,λ的取值范围为(1,3]∪(4,+∞).
7.答案 (4,8)
解析 设g(x)=f(x)-ax,由题意可知方程f(x)=ax恰有2个互异的实数解即函数y=g(x)有2个零点,即y=g(x)的图象与x轴有2个交点,满足条件的y=g(x)的图象有以下两种情况:
情况一:
则∴4
则不等式组无解.
综上,满足条件的a的取值范围是(4,8).
8.B 因为R0=3.28,T=6且R0=1+rT,所以指数增长率r==0.38,设累计感染病例数增加1倍需要的时间为t天,则I(t)=2I(0),即ert=2,即e0.38t=2,两边取自然对数得ln e0.38t=ln 2,即0.38t=ln 2,又ln 2≈0.69,所以t=≈≈1.8.故选B.
9.C I(t*)==0.95K,整理可得=19,两边取自然对数得0.23(t*-53)=ln 19,解得t*≈66,故选C.
三年模拟练
1.C 若零点所处的初始区间为,
则f f =·(-1+a-1)<0,
解得2
∴f(x)的零点所在的区间为.故选B.
3.A 由题意知2xy=20,∴xy=10,∴y=(2≤x≤10),故选A.
4.A 令f(x)=ex+x-2=0,则ex=2-x,
令g(x)=ln x+x-2=0,则ln x=2-x,
设y1=ex,y2=ln x,y3=2-x,
在同一平面直角坐标系中作出函数y1=ex,y2=ln x,y3=2-x的图象,如图.
∵函数f(x)=ex+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,
∴y1=ex与y3=2-x图象的交点的横坐标为a,y2=ln x与y3=2-x图象的交点的横坐标为b,由图象知a<1
当a=0时, f(x)=2-x,此时f(x)与g(x)的图象仅有1个交点,舍去.
当a<0时, f(x)的图象开口向下且恒过点(0,2),此时f(x)与g(x)的图象一定有2个不同的交点.
当a>0时, f(x)的图象开口向上且恒过点(0,2),对称轴为直线x=,且>0.
当f(x)与g(x)的图象仅有1个交点时,可求得a=.
要使f(x)与g(x)的图象有2个不同的交点,只需0
故选B.
6.B 由题意得=20%,
∴=1.2,∴log2(1+λ)=1.2log22 000,
∴1+λ=2 0001.2,∴λ=2 0001.2-1,
又∵lg2 0001.2=1.2lg 2 000=1.2(lg 2+3)≈1.2×(0.3+3)=3.96,
∴2 0001.2=103.96≈9 120,∴λ=2 0001.2-1=9 119.
7.答案 (1)y=2 500×0.8x (2)7.2
解析 (1)由题意知,经过x小时后,药物在病人血液中的量y=2 500×(1-20%)x=2 500×0.8x,即y与x的关系式为y=2 500×0.8x.
(2)令2 500×0.8x≥500,即0.8x≥0.2.
∵0.87.2≈0.2,y=0.8x是单调递减函数,
∴x≤7.2,
∴要使病人没有危险,再次注射该药物的时间不能超过7.2小时.
8.解析 (1)由函数f(x)=x2-3mx+n的两个零点分别为1和2,
可得1-3m+n=0,4-6m+n=0,解得m=1,n=2.
(2)由(1)可得f(x)=x2-3x+2.
由不等式f(x)-k>0在x∈[0,5]上恒成立,可得不等式k
∴f(x)=x2-3x+2在x∈[0,5]上的最小值为f =-,∴k<-.
(3)由(1)得g(x)==x+-3.
∵函数F(x)=g(2x)-r·2x在x∈[-1,1]上有零点,
∴g(2x)-r·2x=0在x∈[-1,1]上有解,即r=1+2·-3·在x∈[-1,1]上有解,
令t=,则t∈,
r=2t2-3t+1=2-,
∴-≤r≤3,
∴实数r的取值范围是.
9.解析 (1)一次性支付好.理由如下:
分两次支付时,支付金额为250-5×+650-5×-40=230+600-40=790(元).
一次性支付时,支付金额为250+650-5×-40×2=745(元).
因为745<790,所以一次性支付好.
(2)设购买x(x∈N+)件,平均价格为y元/件.
由于预算不超过500元,所以最多购买19件.
当1≤x≤14,x∈N+时,不能享受优惠二,
y==30-×
=
=
又27.5+>27.5,
所以当购买偶数件时,y取得最小值,且ymin=27.5.
当15≤x≤19,x∈N+时,能享受优惠二,
y==30-×-
=
=
若x为偶数,则x=16时,y取得最小值,且ymin=25.
若x为奇数,则y随n的增大而增大,所以当x=15时,y取得最小值,且ymin=25.
又25<27.5,所以购买15件或16件该商品,才能使其平均价格最低,最低平均价格为25元/件.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
