2021-2022学年沪教版(上海)六年级数学第二学期8.4(1)长方体中棱与平面的位置关系的认识 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年沪教版(上海)六年级数学第二学期8.4(1)长方体中棱与平面的位置关系的认识 课件(共21张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 655.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
8.4(1)长方体中棱与平面的位置关系的认识
直线和平面的位置关系
直线与平面平行
直线与平面相交
l
α
l
α
直线PQ垂直于平面ABCD
记作:直线PQ⊥平面ABCD
读作:直线PQ垂直于平面ABCD
A
B
C
D
P
Q
直线与平面垂直
想一想
A
B
C
E
F
G
H
D
长方体中棱与平面的位置关系
棱EF与平面BCGF垂直
棱BF与平面ABCD垂直
记作:棱EF⊥平面BCGF
记作:棱BF⊥平面ABCD
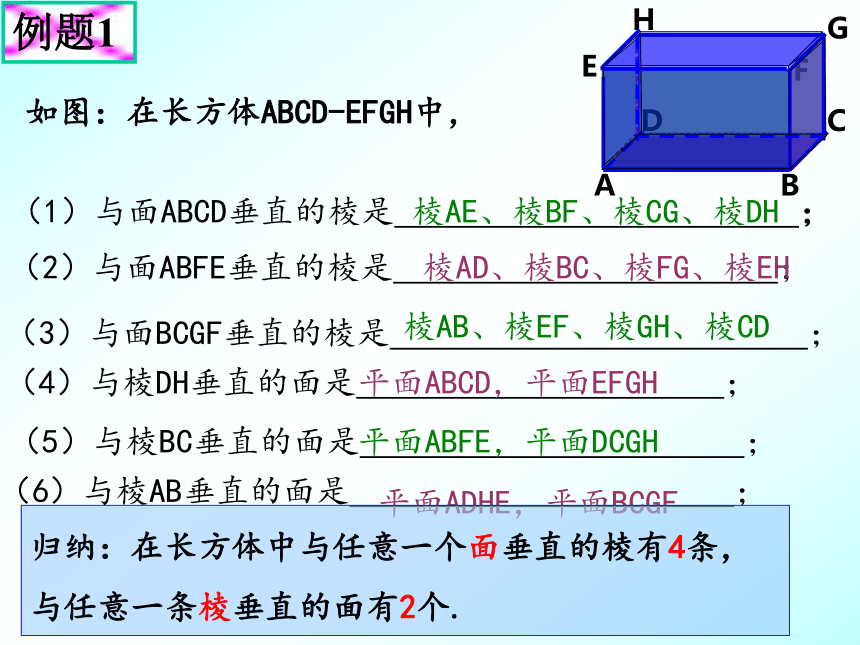
如图:在长方体ABCD-EFGH中,
(4)与棱DH垂直的面是 ;
(5)与棱BC垂直的面是 ;
(6)与棱AB垂直的面是 ;
(1)与面ABCD垂直的棱是 ;
(2)与面ABFE垂直的棱是 ;
(3)与面BCGF垂直的棱是 ;
A
B
C
E
F
G
H
D
平面ABCD,平面EFGH
平面ABFE,平面DCGH
平面ADHE,平面BCGF
棱AE、棱BF、棱CG、棱DH
棱AD、棱BC、棱FG、棱EH
棱AB、棱EF、棱GH、棱CD
例题1
归纳:在长方体中与任意一个面垂直的棱有4条,与任意一条棱垂直的面有2个.
问题:
实际生活中如何检验直线与平面垂直呢?
A
B
C
D
P
Q
可以用“铅垂线”检验
用铅垂线可以检验细棒是否垂直于水平面。如果铅垂线能与细棒紧贴,那么细棒垂直于水平面。
1、可以用 “铅垂线”检验:
用一根细绳,一端系一重物(如钥匙、螺帽),另一端用手提起,使重物悬空,静止后这根细绳是垂直于水平面的。这种垂直于水平面的直线,我们通常称为铅垂线。
若铅垂线能与细棒紧贴,那么细棒垂直于水平面.
问题:
实际生活中如何检验直线与平面垂直呢?
A
B
C
D
P
Q
可以用“三角尺”检验
用三角尺可以检验细棒是否垂直于墙面。如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴细棒,那么细棒垂直于墙面。
如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴细棒,那么细棒垂直于墙面。
2、可以用 “三角尺”检验:
若另一条直角边都能紧贴细棒,那么细棒垂直于墙面。
问题:
实际生活中如何检验直线与平面垂直呢?
A
B
C
D
P
Q
可以用“合页型折纸”检验
用合页型折纸可以检验细棒是否垂直于桌面。将合页型折纸直立于桌面,如果折痕能与细棒紧贴,那么细棒垂直于桌面。
3、用“合页型折纸”检验:
将一张长方形的硬纸片对折,然后张开一个角度,由于它的形状像门窗转轴的合页,我们把这个制作称为合页型折纸,如果将合页型折纸直立于桌面,那么可以看到折痕垂直于桌面.
若折痕能与细棒紧贴,那么细棒垂直于桌面.
1、可以用“铅垂线”检验
问题:
如何检验直线与平面垂直呢?
2、可以用“三角尺”检验
3、可以用“合页型折纸”检验
在长方体ABCD-EFGH中,如何说明棱AE⊥平面ABCD?
可以把面ADHE与面ABFE组成的图形看作直立于面ABCD上的合页型折纸,从而说明棱AE⊥平面ABCD
在长方体ABCD-EFGH中,如何说明棱BF⊥平面ABCD?
∠ABF和∠CBF都是直角,可以把它们看作两把三角尺,它们各有一条直角边分别紧贴面ABCD,且AB与BC相交,另一条直角边都能紧贴棱BF,从而说明棱BF⊥平面ABCD
1、“三角尺”检验法与“合页型折纸”检验法有何相同之处?
(1)“铅垂线”法
(3)“合页型折纸”法
(2)“三角尺”法
2、检验直线与平面垂直的方法有哪些?
两把三角尺相交位置摆放
各有一条直角边紧贴被检验平面
观察另一组叠合的直角边是否与被检验的直线能够紧贴
合页型折纸张开一个角度
直立于被检验平面
观察折痕与被检验的直线是否能够紧贴
思考:
思考:
1、如何检验山顶上直立的旗杆是否与水平面垂直?
2、如何检验教室门的边线与地面是否垂直?
课堂小结
(1)“铅垂线”法、(2)“三角尺”法、(3)“合页型折纸”法.
1.直线与平面垂直.
棱与平面垂直.
2.三种检验直线与平面垂直的方法
8.4(1)长方体中棱与平面的位置关系的认识
直线和平面的位置关系
直线与平面平行
直线与平面相交
l
α
l
α
直线PQ垂直于平面ABCD
记作:直线PQ⊥平面ABCD
读作:直线PQ垂直于平面ABCD
A
B
C
D
P
Q
直线与平面垂直
想一想
A
B
C
E
F
G
H
D
长方体中棱与平面的位置关系
棱EF与平面BCGF垂直
棱BF与平面ABCD垂直
记作:棱EF⊥平面BCGF
记作:棱BF⊥平面ABCD
如图:在长方体ABCD-EFGH中,
(4)与棱DH垂直的面是 ;
(5)与棱BC垂直的面是 ;
(6)与棱AB垂直的面是 ;
(1)与面ABCD垂直的棱是 ;
(2)与面ABFE垂直的棱是 ;
(3)与面BCGF垂直的棱是 ;
A
B
C
E
F
G
H
D
平面ABCD,平面EFGH
平面ABFE,平面DCGH
平面ADHE,平面BCGF
棱AE、棱BF、棱CG、棱DH
棱AD、棱BC、棱FG、棱EH
棱AB、棱EF、棱GH、棱CD
例题1
归纳:在长方体中与任意一个面垂直的棱有4条,与任意一条棱垂直的面有2个.
问题:
实际生活中如何检验直线与平面垂直呢?
A
B
C
D
P
Q
可以用“铅垂线”检验
用铅垂线可以检验细棒是否垂直于水平面。如果铅垂线能与细棒紧贴,那么细棒垂直于水平面。
1、可以用 “铅垂线”检验:
用一根细绳,一端系一重物(如钥匙、螺帽),另一端用手提起,使重物悬空,静止后这根细绳是垂直于水平面的。这种垂直于水平面的直线,我们通常称为铅垂线。
若铅垂线能与细棒紧贴,那么细棒垂直于水平面.
问题:
实际生活中如何检验直线与平面垂直呢?
A
B
C
D
P
Q
可以用“三角尺”检验
用三角尺可以检验细棒是否垂直于墙面。如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴细棒,那么细棒垂直于墙面。
如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴细棒,那么细棒垂直于墙面。
2、可以用 “三角尺”检验:
若另一条直角边都能紧贴细棒,那么细棒垂直于墙面。
问题:
实际生活中如何检验直线与平面垂直呢?
A
B
C
D
P
Q
可以用“合页型折纸”检验
用合页型折纸可以检验细棒是否垂直于桌面。将合页型折纸直立于桌面,如果折痕能与细棒紧贴,那么细棒垂直于桌面。
3、用“合页型折纸”检验:
将一张长方形的硬纸片对折,然后张开一个角度,由于它的形状像门窗转轴的合页,我们把这个制作称为合页型折纸,如果将合页型折纸直立于桌面,那么可以看到折痕垂直于桌面.
若折痕能与细棒紧贴,那么细棒垂直于桌面.
1、可以用“铅垂线”检验
问题:
如何检验直线与平面垂直呢?
2、可以用“三角尺”检验
3、可以用“合页型折纸”检验
在长方体ABCD-EFGH中,如何说明棱AE⊥平面ABCD?
可以把面ADHE与面ABFE组成的图形看作直立于面ABCD上的合页型折纸,从而说明棱AE⊥平面ABCD
在长方体ABCD-EFGH中,如何说明棱BF⊥平面ABCD?
∠ABF和∠CBF都是直角,可以把它们看作两把三角尺,它们各有一条直角边分别紧贴面ABCD,且AB与BC相交,另一条直角边都能紧贴棱BF,从而说明棱BF⊥平面ABCD
1、“三角尺”检验法与“合页型折纸”检验法有何相同之处?
(1)“铅垂线”法
(3)“合页型折纸”法
(2)“三角尺”法
2、检验直线与平面垂直的方法有哪些?
两把三角尺相交位置摆放
各有一条直角边紧贴被检验平面
观察另一组叠合的直角边是否与被检验的直线能够紧贴
合页型折纸张开一个角度
直立于被检验平面
观察折痕与被检验的直线是否能够紧贴
思考:
思考:
1、如何检验山顶上直立的旗杆是否与水平面垂直?
2、如何检验教室门的边线与地面是否垂直?
课堂小结
(1)“铅垂线”法、(2)“三角尺”法、(3)“合页型折纸”法.
1.直线与平面垂直.
棱与平面垂直.
2.三种检验直线与平面垂直的方法
