2021-2022学年沪教版(上海)六年级数学第二学期8.5(1)长方体中平面与平面位置关系的认识 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年沪教版(上海)六年级数学第二学期8.5(1)长方体中平面与平面位置关系的认识 课件(共19张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
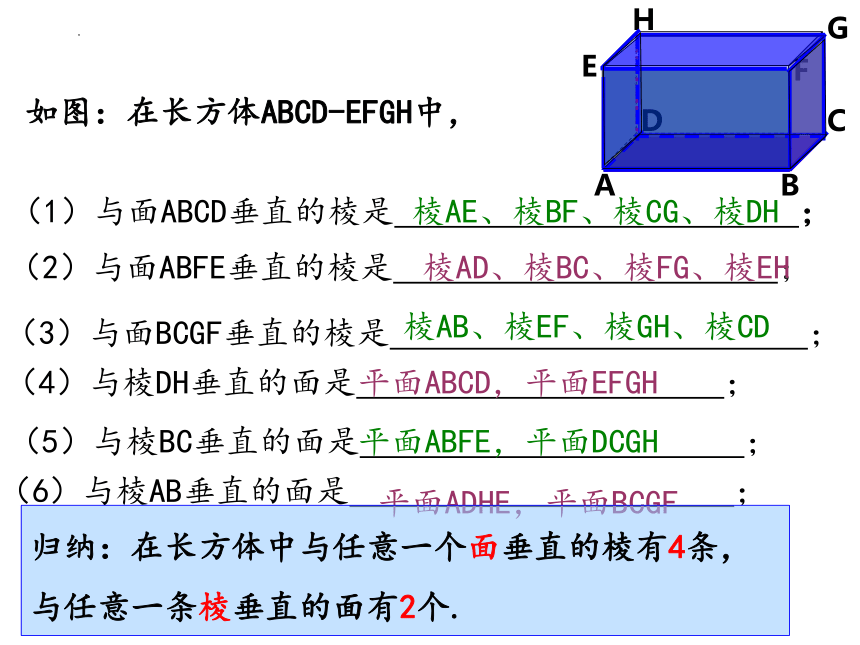
如图:在长方体ABCD-EFGH中,
(4)与棱DH垂直的面是 ;
(5)与棱BC垂直的面是 ;
(6)与棱AB垂直的面是 ;
(1)与面ABCD垂直的棱是 ;
(2)与面ABFE垂直的棱是 ;
(3)与面BCGF垂直的棱是 ;
A
B
C
E
F
G
H
D
平面ABCD,平面EFGH
平面ABFE,平面DCGH
平面ADHE,平面BCGF
棱AE、棱BF、棱CG、棱DH
棱AD、棱BC、棱FG、棱EH
棱AB、棱EF、棱GH、棱CD
归纳:在长方体中与任意一个面垂直的棱有4条,与任意一条棱垂直的面有2个.
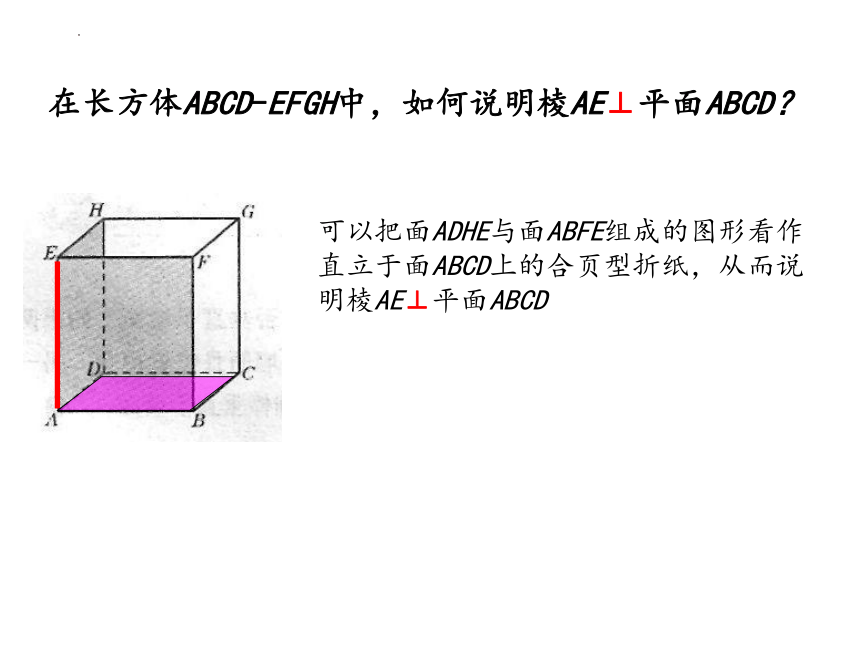
在长方体ABCD-EFGH中,如何说明棱AE⊥平面ABCD?
可以把面ADHE与面ABFE组成的图形看作直立于面ABCD上的合页型折纸,从而说明棱AE⊥平面ABCD
8.5(1) 长方体中平面与平面位置关系的认识
平面α垂直于平面β
记作:平面α⊥平面β
读作:平面α垂直于平面β
平面与平面垂直
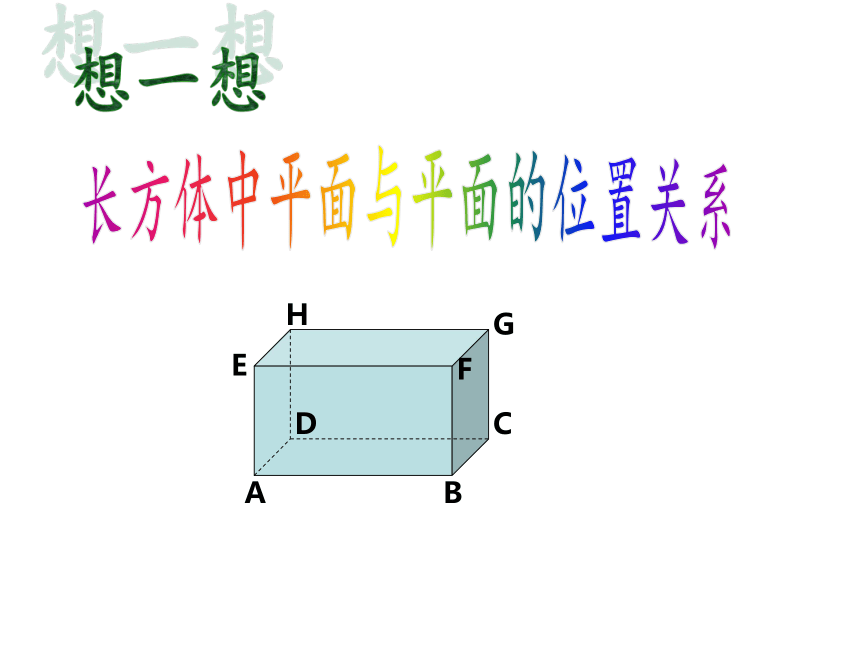
想一想
A
B
C
E
F
G
H
D
长方体中平面与平面的位置关系
面ABFE与面BCGF垂直
记作:面ABFE⊥面BCGF
面EFGH与面ABFE垂直
记作:面EFGH⊥面ABFE
如图:在长方体ABCD-EFGH中,
(1)与面ABCD垂直的平面是
;
(2)与面ABFE垂直的平面是
;
(3)与面BCGF垂直的平面是
;
A
B
C
E
F
G
H
D
平面ABFE、平面BCGF、平面CDHG、平面ADHE
平面ADHE、平面EFGH、平面BCGF、平面ABFE
平面ABFE、平面EFGH、平面CDHG、平面ABCD
例题1
归纳:在长方体中任意两个相邻的面都互相垂直,与任意一个面垂直的面都有4个。
问题:
实际生活中如何检验平面与平面垂直呢?
可以用“铅垂线”检验
用”铅垂线”可以检验课桌的侧面是否垂直于地面。如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
1、可以用 “铅垂线”检验:
用”铅垂线”可以检验课桌的侧面是否垂直于地面。如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
问题:
实际生活中如何检验平面与平面垂直呢?
可以用“合页型折纸”检验
用”合页型折纸”可以检验书架的隔板是否垂直于侧面。将合页型折纸直立于隔板上,如果折痕能紧贴侧面,那么隔板垂直于侧面。
2、可以用“合页型折纸”检验
用”合页型折纸”可以检验书架的隔板是否垂直于侧面。将合页型折纸直立于隔板上,如果折痕能紧贴侧面,那么隔板垂直于侧面。
如果折痕能紧贴侧面,那么隔板垂直于侧面。
问题:
实际生活中如何检验平面与平面垂直呢?
可以用“三角尺”检验
用三角尺可以检验墙面是否垂直于墙面。如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴另一墙面,那么墙面垂直于墙面。
如果两把三角尺各有一条直角边紧贴她前方的墙面且位置相交,另一条直角边都能紧贴她右侧的墙面,那么右侧的墙面垂直于前方的墙面。
3、可以用“三角尺”检验
如果另一条直角边都能紧贴她右侧的墙面,那么右侧的墙面垂直于前方的墙面。
1、可以用“铅垂线”检验
问题:
如何检验平面与平面垂直呢?
3、可以用“三角尺”检验
2、可以用“合页型折纸”检验
在长方体ABCD-EFGH中,如何说明面BCGF⊥面ABCD?
可以把面ABFE与面BCGF组成的图形看作是直立于面ABCD上的合页型折纸,折痕BF能紧贴面BCGF,从而说明面BCGF⊥面ABCD。
如果把图中的骰子看作是一个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,请问:
(1)与点数是4的面垂直的面有哪些
(2) 哪些面与点数是5的面垂直
(3)数一数这6个面中,互相垂直的面共有几对
例题2
课堂小结
(1)“铅垂线”法、(2)“合页型折纸”法.
(3)“三角尺”法、
1.平面与平面垂直.
2.三种检验平面与平面垂直的方法
如图:在长方体ABCD-EFGH中,
(4)与棱DH垂直的面是 ;
(5)与棱BC垂直的面是 ;
(6)与棱AB垂直的面是 ;
(1)与面ABCD垂直的棱是 ;
(2)与面ABFE垂直的棱是 ;
(3)与面BCGF垂直的棱是 ;
A
B
C
E
F
G
H
D
平面ABCD,平面EFGH
平面ABFE,平面DCGH
平面ADHE,平面BCGF
棱AE、棱BF、棱CG、棱DH
棱AD、棱BC、棱FG、棱EH
棱AB、棱EF、棱GH、棱CD
归纳:在长方体中与任意一个面垂直的棱有4条,与任意一条棱垂直的面有2个.
在长方体ABCD-EFGH中,如何说明棱AE⊥平面ABCD?
可以把面ADHE与面ABFE组成的图形看作直立于面ABCD上的合页型折纸,从而说明棱AE⊥平面ABCD
8.5(1) 长方体中平面与平面位置关系的认识
平面α垂直于平面β
记作:平面α⊥平面β
读作:平面α垂直于平面β
平面与平面垂直
想一想
A
B
C
E
F
G
H
D
长方体中平面与平面的位置关系
面ABFE与面BCGF垂直
记作:面ABFE⊥面BCGF
面EFGH与面ABFE垂直
记作:面EFGH⊥面ABFE
如图:在长方体ABCD-EFGH中,
(1)与面ABCD垂直的平面是
;
(2)与面ABFE垂直的平面是
;
(3)与面BCGF垂直的平面是
;
A
B
C
E
F
G
H
D
平面ABFE、平面BCGF、平面CDHG、平面ADHE
平面ADHE、平面EFGH、平面BCGF、平面ABFE
平面ABFE、平面EFGH、平面CDHG、平面ABCD
例题1
归纳:在长方体中任意两个相邻的面都互相垂直,与任意一个面垂直的面都有4个。
问题:
实际生活中如何检验平面与平面垂直呢?
可以用“铅垂线”检验
用”铅垂线”可以检验课桌的侧面是否垂直于地面。如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
1、可以用 “铅垂线”检验:
用”铅垂线”可以检验课桌的侧面是否垂直于地面。如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
问题:
实际生活中如何检验平面与平面垂直呢?
可以用“合页型折纸”检验
用”合页型折纸”可以检验书架的隔板是否垂直于侧面。将合页型折纸直立于隔板上,如果折痕能紧贴侧面,那么隔板垂直于侧面。
2、可以用“合页型折纸”检验
用”合页型折纸”可以检验书架的隔板是否垂直于侧面。将合页型折纸直立于隔板上,如果折痕能紧贴侧面,那么隔板垂直于侧面。
如果折痕能紧贴侧面,那么隔板垂直于侧面。
问题:
实际生活中如何检验平面与平面垂直呢?
可以用“三角尺”检验
用三角尺可以检验墙面是否垂直于墙面。如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴另一墙面,那么墙面垂直于墙面。
如果两把三角尺各有一条直角边紧贴她前方的墙面且位置相交,另一条直角边都能紧贴她右侧的墙面,那么右侧的墙面垂直于前方的墙面。
3、可以用“三角尺”检验
如果另一条直角边都能紧贴她右侧的墙面,那么右侧的墙面垂直于前方的墙面。
1、可以用“铅垂线”检验
问题:
如何检验平面与平面垂直呢?
3、可以用“三角尺”检验
2、可以用“合页型折纸”检验
在长方体ABCD-EFGH中,如何说明面BCGF⊥面ABCD?
可以把面ABFE与面BCGF组成的图形看作是直立于面ABCD上的合页型折纸,折痕BF能紧贴面BCGF,从而说明面BCGF⊥面ABCD。
如果把图中的骰子看作是一个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,请问:
(1)与点数是4的面垂直的面有哪些
(2) 哪些面与点数是5的面垂直
(3)数一数这6个面中,互相垂直的面共有几对
例题2
课堂小结
(1)“铅垂线”法、(2)“合页型折纸”法.
(3)“三角尺”法、
1.平面与平面垂直.
2.三种检验平面与平面垂直的方法
