2022--2023学年北师大版九年级数学下册 2.4 二次函数的应用 同步练习 (Word版,含解析)
文档属性
| 名称 | 2022--2023学年北师大版九年级数学下册 2.4 二次函数的应用 同步练习 (Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 598.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 14:07:44 | ||
图片预览


文档简介
北师大版 2.4 二次函数的应用
一、选择题(共12小题)
1. 下列函数关系中,可以看做二次函数 模型的是
A. 在一定的距离内汽车的行驶速度与行驶时间的关系
B. 我国人口年自然增长率 ,这样我国人口总数随年份的关系
C. 竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D. 圆的周长与圆的半径之间的关系
2. 如图,一边靠墙(墙足够长),其他三边用 长的篱笆围成一个矩形花园,则这个花园的最大面积是
A. B. C. D. 以上都不对
3. 某商店经营皮鞋,已知所获利润 (元)与销售的单价 (元)之间的关系为 ,则获利最多为
A. 元 B. 元 C. 元 D. 元
4. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为
A. B. C. D.
5. 如图所示,一座抛物线形的拱桥在正常水位时,水面 宽为 米,拱桥的最高点 到水面 的距离为 米.如果此时水位上升 米就达到警戒水位 ,那么 宽为
A. 米 B. 米 C. 米 D. 米
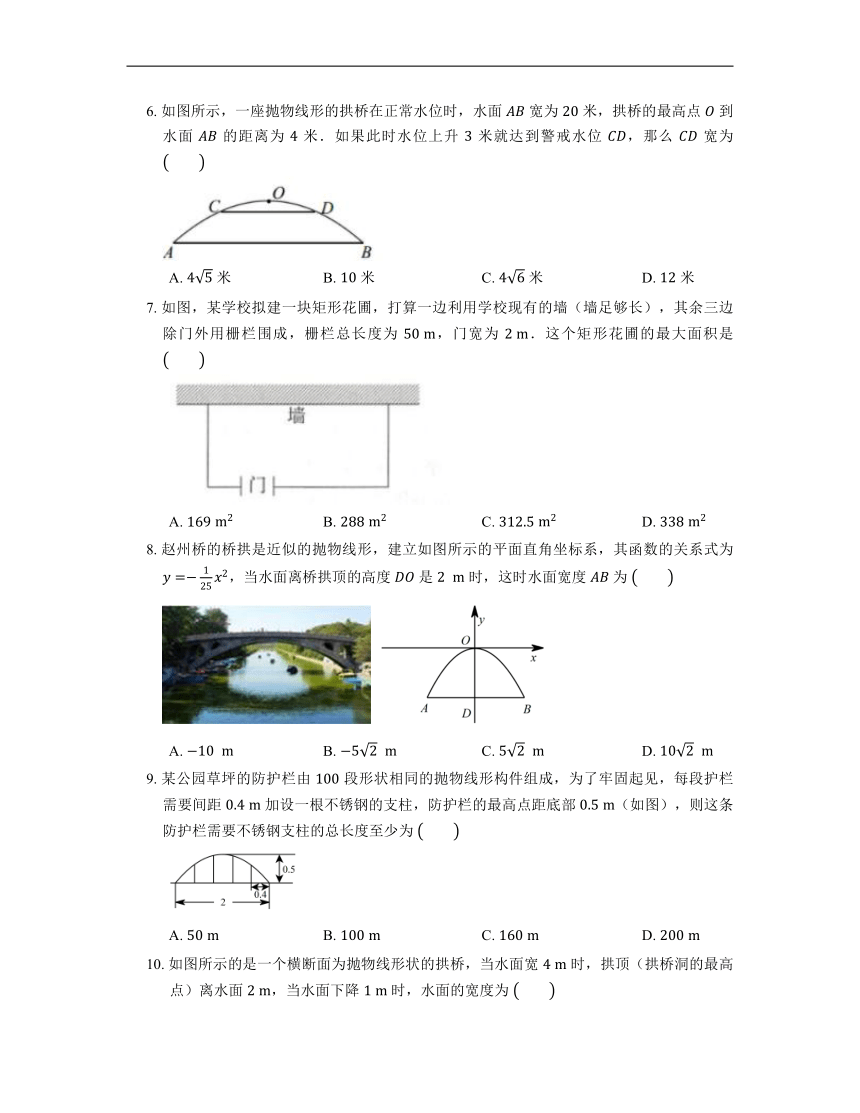
6. 如图所示,一座抛物线形的拱桥在正常水位时,水面 宽为 米,拱桥的最高点 到水面 的距离为 米.如果此时水位上升 米就达到警戒水位 ,那么 宽为
A. 米 B. 米 C. 米 D. 米
7. 如图,某学校拟建一块矩形花圃,打算一边利用学校现有的墙(墙足够长),其余三边除门外用栅栏围成,栅栏总长度为 ,门宽为 .这个矩形花圃的最大面积是
A. B. C. D.
8. 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为 ,当水面离桥拱顶的高度 是 时,这时水面宽度 为
A. B. C. D.
9. 某公园草坪的防护栏由 段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距 加设一根不锈钢的支柱,防护栏的最高点距底部 (如图),则这条防护栏需要不锈钢支柱的总长度至少为
A. B. C. D.
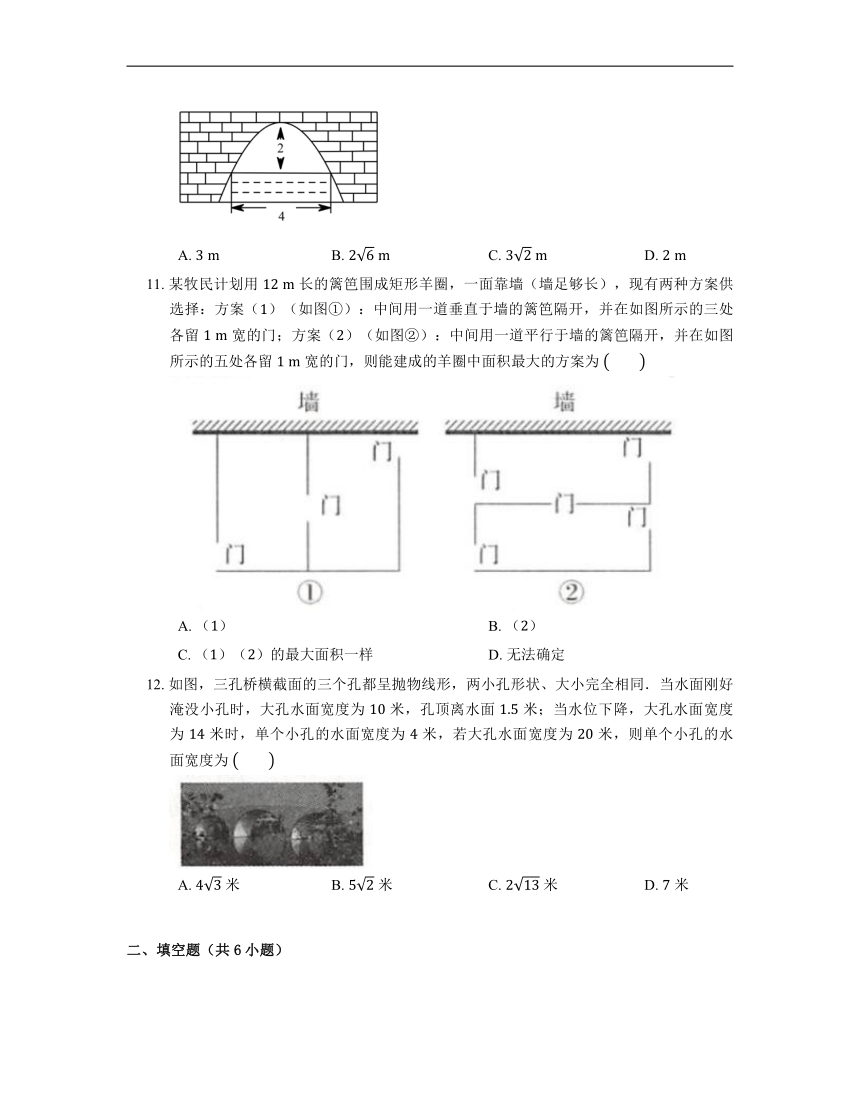
10. 如图所示的是一个横断面为抛物线形状的拱桥,当水面宽 时,拱顶(拱桥洞的最高点)离水面 ,当水面下降 时,水面的宽度为
A. B. C. D.
11. 某牧民计划用 长的篱笆围成矩形羊圈,一面靠墙(墙足够长),现有两种方案供选择:方案()(如图①):中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留 宽的门;方案()(如图②):中间用一道平行于墙的篱笆隔开,并在如图所示的五处各留 宽的门,则能建成的羊圈中面积最大的方案为
A. () B. ()
C. ()()的最大面积一样 D. 无法确定
12. 如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为 米,孔顶离水面 米;当水位下降,大孔水面宽度为 米时,单个小孔的水面宽度为 米,若大孔水面宽度为 米,则单个小孔的水面宽度为
A. 米 B. 米 C. 米 D. 米
二、填空题(共6小题)
13. 为防治新冠病毒,某医药公司一月份的产值为 亿元,若每月平均增长率为 ,第一季度的总产值为 (亿元),则 关于 的函数解析式为 .
14. 在一个边长为 的正方形中挖去一个小正方形,使小正方形四周剩下部分的宽度均为 ,若剩下阴影部分的面积为 ,那么 关于 的函数解析式是 .
15. 一位运动员投掷铅球,如果铅球运行时离地面高度为 (米)关于水平距离 (米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 .
16. 据了解,某蔬菜种植基地 年的蔬菜产量为 万吨, 年的蔬菜产量为 万吨,如果 年至 年蔬菜产量的年平均增长率为 ,那么 关于 的函数解析式为 .
17. 根据物理学规律,如果把一个物体从地面以 的速度竖直上抛(如图所示),那么物体经过 离地面的高度(单位:)为 .根据上述规律,该物体落回地面所需要的时间 约为 (结果保留整数).
18. 飞机着陆后滑行的距离 (单位:)关于滑行时间 (单位:)的函数表达式是 .在飞机着陆滑行中,最后 滑行的距离是 .
三、解答题(共5小题)
19. 一直角三角形的两直角边的和为 ,若它的一条直角边长为 ,它的面积为 ;
(1)求 与 之间的函数关系式;
(2)当 为何值时,三角形的面积最大 最大面积为多少
20. 某种烟花被竖直向上发射时,它的高度 与时间 的关系可以用函数 表示.经过多少秒,烟花达到它的最高点
21. 已知直角三角形两条直角边的和等于 ,若它的条直角边为 (),它的面积为 ().
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)求当 时, 的值.
22. 如图,已知一抛物线形大门,其地面宽度 ,一同学站在门内,在离门脚 点 远的 处,垂直地面立起一根 长的木杆,其顶端恰好顶在抛物线形门上 处.根据这些条件,请你求出该大门的高 .
23. 一位运动员在距篮下 米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为 时,达到最大高度 ,然后准确落入篮圈.已知篮圈中心到地面的距离为 .
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高 ,在这次跳投中,球在头顶上方 处出手,问:球出手时,他跳离地面的高度是多少
答案
1. C
2. C
【解析】设 的长为 ,这个花园的面积是 ,
则 ,
当 时, 取得最大值,此时 ,故选C.
3. B
4. C
【解析】由题意,得 .故当 时, 取得最大值,此时 .
5. B
【解析】以 点为坐标原点, 的垂直平分线为 轴,过 点作 轴的垂线,建立直角坐标系,
设抛物线的解析式为 ,
点到水面 的距离为 米,
, 点的纵坐标为 ,
水面 宽为 米,
,,
将 代入 ,
,
,
,
水位上升 米就达到警戒水位 ,
点的纵坐标为 ,
,
,
.
6. B
7. D
【解析】设矩形花圃的面积为 ,垂直于墙的一边的长为 ,则平行于墙的一边的长为 ,则 ,
当 时, 有最大值 ,即矩形花圃的最大面积为 .
故选D.
8. D
【解析】根据题意,当 时,有 ,
解得:,
,,
所有水面宽度 .
9. C
【解析】提示:适当建立平面直角坐标系(可以以抛物线的顶点为坐标原点),利用间距为 的不锈钢支柱,可以求出一段抛物线需要不锈钢支柱的长度,然后乘 即可.
10. B
11. A
【解析】对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 ;
对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 .
因为 ,
所以面积最大的方案是().
12. B
【解析】建立如图所示的平面直角坐标系,
则 米, 米, 米, 米,
设大孔所在抛物线的解析式为 ,
米,
点 ,
,
,
大孔所在抛物线的解析式为 ,
设点 ,则设顶点为 的小孔所在抛物线的解析式为 ,
米,
点 的横坐标为 ,
点 的坐标为 ,
当 时,解得 ,,
米,
,
,
顶点为 的小孔所在抛物线的解析式为 ,
大孔水面宽度为 米,
当 时,,
,
,,
当大孔水面宽度为 米时,单个小孔的水面宽度 (米).
故选B.
13.
【解析】 某医药公司一月份的产值为 亿元,若每月平均增长率为 ,
二月份的为 ,
三月份的为 ,
第一季度的总产值为 (亿元),则 .
14.
【解析】设剩下部分的面积为 ,则:.
15.
【解析】由题意可得:,
故铅球运动过程中最高点离地面的距离为:.
16.
17.
18.
19. (1)
(2) 时,三角形最大面积为 .
20. 经过 秒达最高点.
21. (1) ;
(2)
22. 如图,建立平面直角坐标系.
设抛物线解析式为 .
由题意知 , 两点坐标分别为 ,,
把 , 两点坐标代入抛物线解析式得
解得
所以抛物线的解析式为 .
所以该大门的高 为 .
23. (1) 当球运行的水平距离为 时,达到最大高度 ,
抛物线的顶点坐标为 ,
设抛物线的表达式为 .
由题图知图象过点
,解得 ,
抛物线的表达式为 .
(2) 设球出手时,他跳离地面的高度为 ,
由()得 ,
则球出手时,球的高度为 ,
,
.
答:球出手时,他跳离地面的高度为 .
一、选择题(共12小题)
1. 下列函数关系中,可以看做二次函数 模型的是
A. 在一定的距离内汽车的行驶速度与行驶时间的关系
B. 我国人口年自然增长率 ,这样我国人口总数随年份的关系
C. 竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力)
D. 圆的周长与圆的半径之间的关系
2. 如图,一边靠墙(墙足够长),其他三边用 长的篱笆围成一个矩形花园,则这个花园的最大面积是
A. B. C. D. 以上都不对
3. 某商店经营皮鞋,已知所获利润 (元)与销售的单价 (元)之间的关系为 ,则获利最多为
A. 元 B. 元 C. 元 D. 元
4. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为
A. B. C. D.
5. 如图所示,一座抛物线形的拱桥在正常水位时,水面 宽为 米,拱桥的最高点 到水面 的距离为 米.如果此时水位上升 米就达到警戒水位 ,那么 宽为
A. 米 B. 米 C. 米 D. 米
6. 如图所示,一座抛物线形的拱桥在正常水位时,水面 宽为 米,拱桥的最高点 到水面 的距离为 米.如果此时水位上升 米就达到警戒水位 ,那么 宽为
A. 米 B. 米 C. 米 D. 米
7. 如图,某学校拟建一块矩形花圃,打算一边利用学校现有的墙(墙足够长),其余三边除门外用栅栏围成,栅栏总长度为 ,门宽为 .这个矩形花圃的最大面积是
A. B. C. D.
8. 赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为 ,当水面离桥拱顶的高度 是 时,这时水面宽度 为
A. B. C. D.
9. 某公园草坪的防护栏由 段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距 加设一根不锈钢的支柱,防护栏的最高点距底部 (如图),则这条防护栏需要不锈钢支柱的总长度至少为
A. B. C. D.
10. 如图所示的是一个横断面为抛物线形状的拱桥,当水面宽 时,拱顶(拱桥洞的最高点)离水面 ,当水面下降 时,水面的宽度为
A. B. C. D.
11. 某牧民计划用 长的篱笆围成矩形羊圈,一面靠墙(墙足够长),现有两种方案供选择:方案()(如图①):中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留 宽的门;方案()(如图②):中间用一道平行于墙的篱笆隔开,并在如图所示的五处各留 宽的门,则能建成的羊圈中面积最大的方案为
A. () B. ()
C. ()()的最大面积一样 D. 无法确定
12. 如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为 米,孔顶离水面 米;当水位下降,大孔水面宽度为 米时,单个小孔的水面宽度为 米,若大孔水面宽度为 米,则单个小孔的水面宽度为
A. 米 B. 米 C. 米 D. 米
二、填空题(共6小题)
13. 为防治新冠病毒,某医药公司一月份的产值为 亿元,若每月平均增长率为 ,第一季度的总产值为 (亿元),则 关于 的函数解析式为 .
14. 在一个边长为 的正方形中挖去一个小正方形,使小正方形四周剩下部分的宽度均为 ,若剩下阴影部分的面积为 ,那么 关于 的函数解析式是 .
15. 一位运动员投掷铅球,如果铅球运行时离地面高度为 (米)关于水平距离 (米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 .
16. 据了解,某蔬菜种植基地 年的蔬菜产量为 万吨, 年的蔬菜产量为 万吨,如果 年至 年蔬菜产量的年平均增长率为 ,那么 关于 的函数解析式为 .
17. 根据物理学规律,如果把一个物体从地面以 的速度竖直上抛(如图所示),那么物体经过 离地面的高度(单位:)为 .根据上述规律,该物体落回地面所需要的时间 约为 (结果保留整数).
18. 飞机着陆后滑行的距离 (单位:)关于滑行时间 (单位:)的函数表达式是 .在飞机着陆滑行中,最后 滑行的距离是 .
三、解答题(共5小题)
19. 一直角三角形的两直角边的和为 ,若它的一条直角边长为 ,它的面积为 ;
(1)求 与 之间的函数关系式;
(2)当 为何值时,三角形的面积最大 最大面积为多少
20. 某种烟花被竖直向上发射时,它的高度 与时间 的关系可以用函数 表示.经过多少秒,烟花达到它的最高点
21. 已知直角三角形两条直角边的和等于 ,若它的条直角边为 (),它的面积为 ().
(1)求 与 之间的函数关系式,并写出自变量 的取值范围;
(2)求当 时, 的值.
22. 如图,已知一抛物线形大门,其地面宽度 ,一同学站在门内,在离门脚 点 远的 处,垂直地面立起一根 长的木杆,其顶端恰好顶在抛物线形门上 处.根据这些条件,请你求出该大门的高 .
23. 一位运动员在距篮下 米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为 时,达到最大高度 ,然后准确落入篮圈.已知篮圈中心到地面的距离为 .
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高 ,在这次跳投中,球在头顶上方 处出手,问:球出手时,他跳离地面的高度是多少
答案
1. C
2. C
【解析】设 的长为 ,这个花园的面积是 ,
则 ,
当 时, 取得最大值,此时 ,故选C.
3. B
4. C
【解析】由题意,得 .故当 时, 取得最大值,此时 .
5. B
【解析】以 点为坐标原点, 的垂直平分线为 轴,过 点作 轴的垂线,建立直角坐标系,
设抛物线的解析式为 ,
点到水面 的距离为 米,
, 点的纵坐标为 ,
水面 宽为 米,
,,
将 代入 ,
,
,
,
水位上升 米就达到警戒水位 ,
点的纵坐标为 ,
,
,
.
6. B
7. D
【解析】设矩形花圃的面积为 ,垂直于墙的一边的长为 ,则平行于墙的一边的长为 ,则 ,
当 时, 有最大值 ,即矩形花圃的最大面积为 .
故选D.
8. D
【解析】根据题意,当 时,有 ,
解得:,
,,
所有水面宽度 .
9. C
【解析】提示:适当建立平面直角坐标系(可以以抛物线的顶点为坐标原点),利用间距为 的不锈钢支柱,可以求出一段抛物线需要不锈钢支柱的长度,然后乘 即可.
10. B
11. A
【解析】对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 ;
对于方案(),设矩形垂直于墙的边长为 ,面积为 ,则平行于墙的边长为 ,
所以 ,即当 时, 最大,最大值为 .
因为 ,
所以面积最大的方案是().
12. B
【解析】建立如图所示的平面直角坐标系,
则 米, 米, 米, 米,
设大孔所在抛物线的解析式为 ,
米,
点 ,
,
,
大孔所在抛物线的解析式为 ,
设点 ,则设顶点为 的小孔所在抛物线的解析式为 ,
米,
点 的横坐标为 ,
点 的坐标为 ,
当 时,解得 ,,
米,
,
,
顶点为 的小孔所在抛物线的解析式为 ,
大孔水面宽度为 米,
当 时,,
,
,,
当大孔水面宽度为 米时,单个小孔的水面宽度 (米).
故选B.
13.
【解析】 某医药公司一月份的产值为 亿元,若每月平均增长率为 ,
二月份的为 ,
三月份的为 ,
第一季度的总产值为 (亿元),则 .
14.
【解析】设剩下部分的面积为 ,则:.
15.
【解析】由题意可得:,
故铅球运动过程中最高点离地面的距离为:.
16.
17.
18.
19. (1)
(2) 时,三角形最大面积为 .
20. 经过 秒达最高点.
21. (1) ;
(2)
22. 如图,建立平面直角坐标系.
设抛物线解析式为 .
由题意知 , 两点坐标分别为 ,,
把 , 两点坐标代入抛物线解析式得
解得
所以抛物线的解析式为 .
所以该大门的高 为 .
23. (1) 当球运行的水平距离为 时,达到最大高度 ,
抛物线的顶点坐标为 ,
设抛物线的表达式为 .
由题图知图象过点
,解得 ,
抛物线的表达式为 .
(2) 设球出手时,他跳离地面的高度为 ,
由()得 ,
则球出手时,球的高度为 ,
,
.
答:球出手时,他跳离地面的高度为 .
