2022--2023学年北师大版九年级数学下册 3.5 确定圆的条件同步练习(Word版,含解析)
文档属性
| 名称 | 2022--2023学年北师大版九年级数学下册 3.5 确定圆的条件同步练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 412.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 14:32:40 | ||
图片预览


文档简介
北师大版 3.5 确定圆的条件
一、选择题(共13小题)
1. 下列说法正确的是
A. 长度相等的弧叫等弧
B. 平分弦的直径一定垂直于该弦
C. 三角形的外心是三条角平分线的交点
D. 不在同一直线上的三个点确定一个圆
2. 三角形的外心是
A. 三条中线的交点 B. 三条边的中垂线的交点
C. 三条高的交点 D. 三条角平分线的交点
3. 下列说法不正确的是
A. 过一点可作无数个圆,那是因为圆心不确定,半径也不确定
B. 过两个点可以画无数个圆,圆心在这两点连线的中垂线上
C. 过不在同一直线上的三个点只能画一个圆
D. 经过三个点一定可以作圆
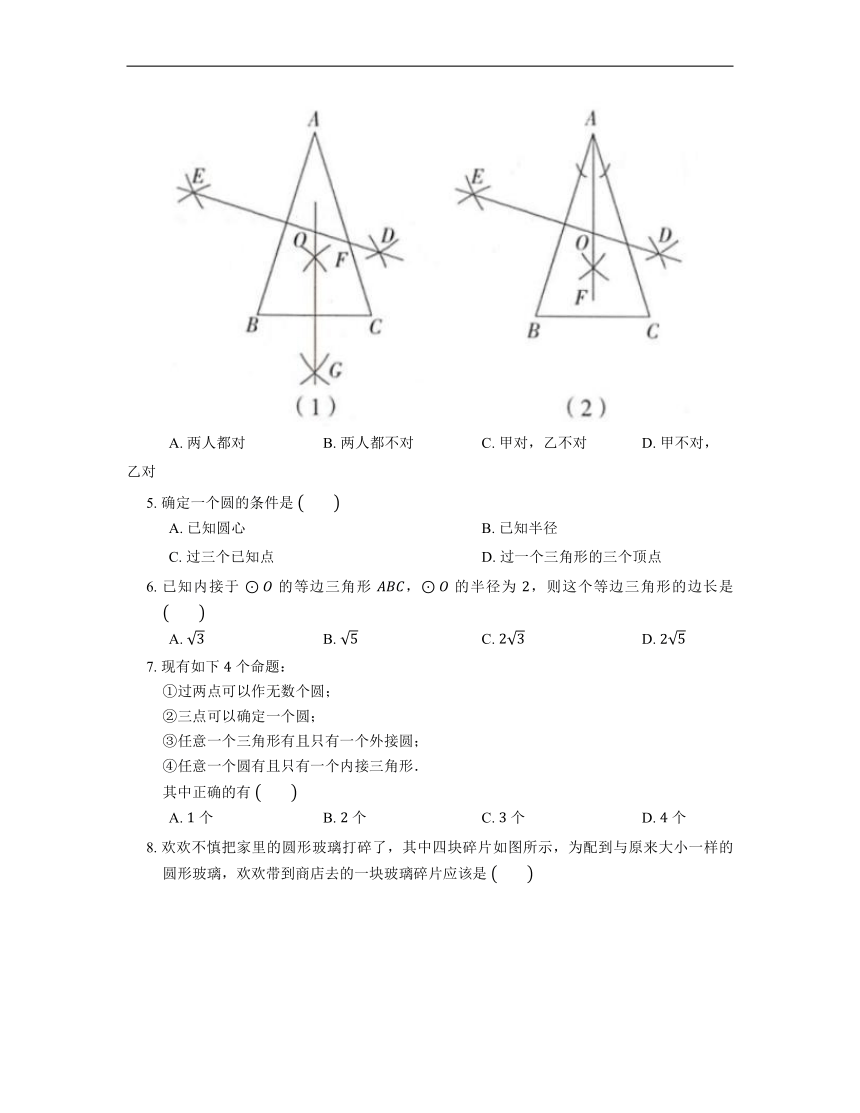
4. 已知:在 中,.求作: 的外心 .以下是甲、乙两名同学的作法:
甲:如图(),
①作 的垂直平分线 ;
②作 的垂直平分线 ;
③ , 交于点 ,则点 即为所求.
乙:如图(),
①作 的垂直平分线 ;
②作 的平分线 ;
③ , 交于点 ,则点 即为所求.
两人的作法正确的是
A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
5. 确定一个圆的条件是
A. 已知圆心 B. 已知半径
C. 过三个已知点 D. 过一个三角形的三个顶点
6. 已知内接于 的等边三角形 , 的半径为 ,则这个等边三角形的边长是
A. B. C. D.
7. 现有如下 个命题:
①过两点可以作无数个圆;
②三点可以确定一个圆;
③任意一个三角形有且只有一个外接圆;
④任意一个圆有且只有一个内接三角形.
其中正确的有
A. 个 B. 个 C. 个 D. 个
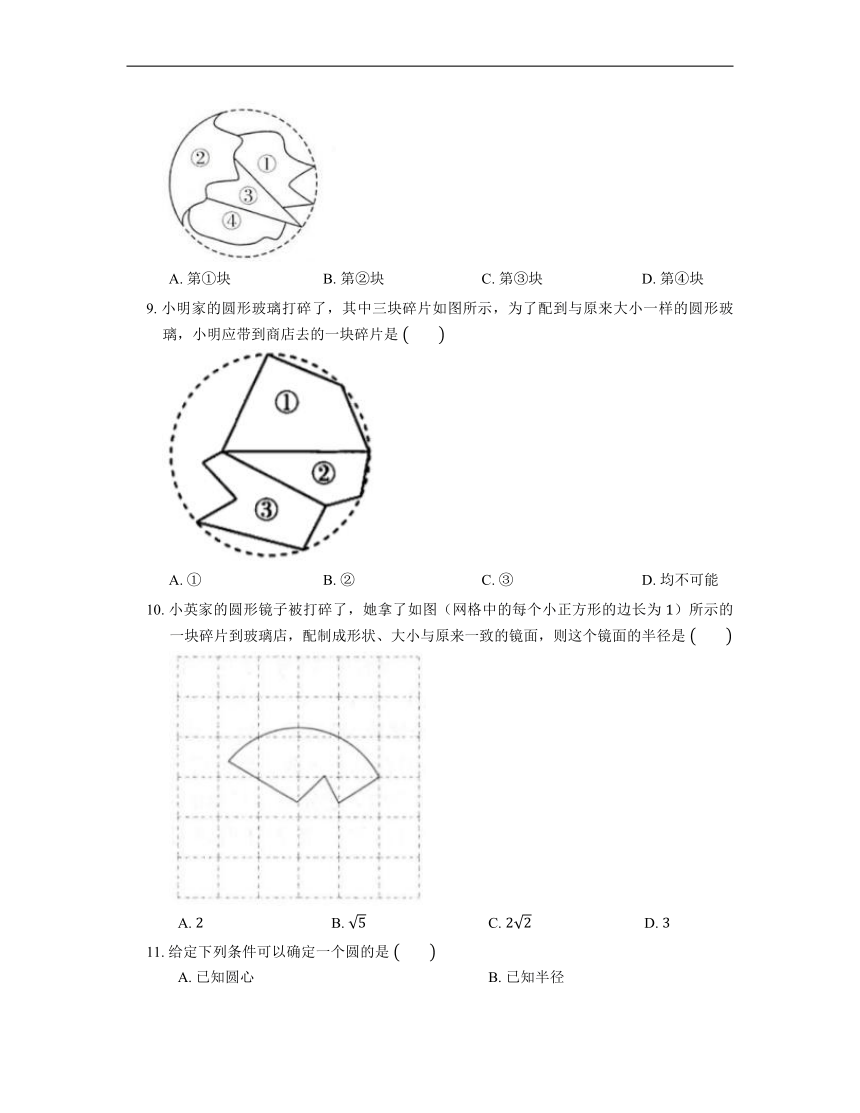
8. 欢欢不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,欢欢带到商店去的一块玻璃碎片应该是
A. 第①块 B. 第②块 C. 第③块 D. 第④块
9. 小明家的圆形玻璃打碎了,其中三块碎片如图所示,为了配到与原来大小一样的圆形玻璃,小明应带到商店去的一块碎片是
A. ① B. ② C. ③ D. 均不可能
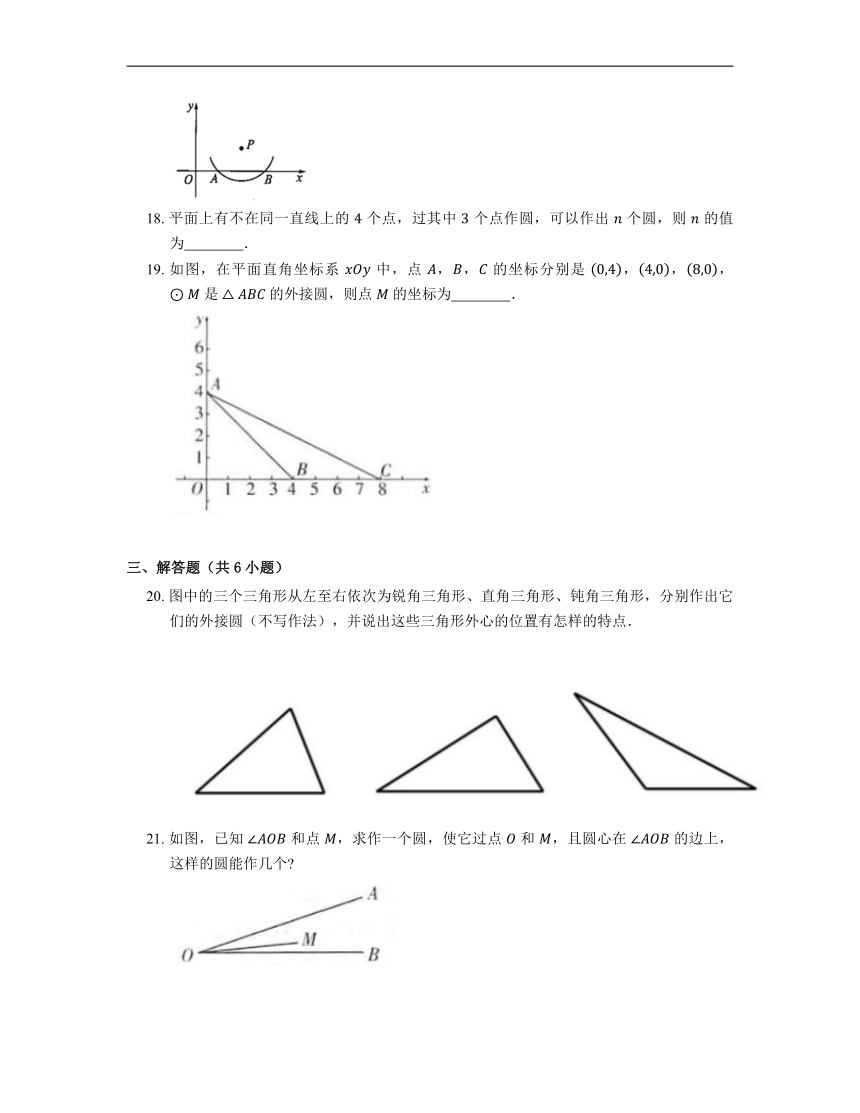
10. 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形的边长为 )所示的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是
A. B. C. D.
11. 给定下列条件可以确定一个圆的是
A. 已知圆心 B. 已知半径
C. 已知三点 D. 不在同一直线上的三点
12. 如图,已知平面直角坐标系内三点 ,,, 经过点 ,,,则点 的坐标为
A. B. C. D.
13. 如图,在网格(每个小正方形的边长均为 )中选取 个格点(格线的交点称为格点),分别为点 ,,,,,,,,任意连接除点 外的 个格点组成三角形,则组成的三角形中以点 为外心的是
A. B. C. D.
二、填空题(共6小题)
14. 经过一个点的圆有 个,圆心 ;经过两点的圆有 个,圆心在 ;如果平面上的三个点能够确定一个圆,那么这三点所满足的条件是 .
15. 正三角形的边长为 ,那么它的外接圆半径是 .
16. 已知直线 ,点 ,点 ,设点 为直线 上一动点,当点 的坐标为 时,过 ,, 三点不能作出一个圆.
17. 如图,在直角坐标系中,以点 为圆心的圆弧与 轴交于 , 两点,已知 和 ,则点 的坐标是 .
18. 平面上有不在同一直线上的 个点,过其中 个点作圆,可以作出 个圆,则 的值为 .
19. 如图,在平面直角坐标系 中,点 ,, 的坐标分别是 ,,, 是 的外接圆,则点 的坐标为 .
三、解答题(共6小题)
20. 图中的三个三角形从左至右依次为锐角三角形、直角三角形、钝角三角形,分别作出它们的外接圆(不写作法),并说出这些三角形外心的位置有怎样的特点.
21. 如图,已知 和点 ,求作一个圆,使它过点 和 ,且圆心在 的边上,这样的圆能作几个
22. 图中的三个三角形从左至右依次为锐角三角形、直角三角形、钝角三角形,分别作出它们的外接圆(不写作法),并说出这些三角形外心的位置有怎样的特点.
23. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道需确定管道圆形截面的圆心和半径,如图是水平放置的破裂管道的截面.请用无刻度的直尺和圆规作图,确定圆心 的位置(保留作图痕迹).
24. 经过已知两点 , 作圆,并且使圆心在已知直线 上.
(1)当直线 与线段 斜交时,可作几个圆
(2)当直线 与线段 垂直,但不经过 的中点时,可作几个圆
(3)当直线 是线段 的垂直平分线时,可作几个圆
25. 如图,等边三角形 的边长为 .
(1)尺规作图作它的外接圆 ;
(2)则 的半径为 .
答案
1. D
【解析】A.能够完全重合的弧叫等弧,所以 A 选项错误;
B.平分弦(非直径)的直径一定垂直于该弦,所以 B 选项错误;
C.三角形的外心是三边垂直平分线的交点,所以 C 选项错误;
D.不在同一直线上的三个点确定一个圆,所以 D 选项正确.
2. B
3. D
4. A
【解析】甲的作法是作三角形两边的垂直平分线,则点 到三角形三个顶点的距离相等,
所以点 为 的外心;
在乙的作法中,
因为 ,
所以作 的平分线即作 边的垂直平分线,则点 到三角形三个顶点的距离相等,
所以点 为 的外心.
所以两人都对.
5. D
【解析】确定一个圆的条件是已知圆心和半径,过一个三角形的三个顶点即可确定一个圆.
6. C
7. B
【解析】①过两点可以作无数个圆,是真命题.
②不在同一直线上的三点可以确定一个圆,是假命题.
③任意一个三角形有且只有一个外接圆,是真命题.
④任意一个圆有无数个内接三角形,是假命题.
8. B
9. A
【解析】碎片①中有不在同一条直线上的三点在圆形玻璃上,可以确定一个圆,即可以配到与原来大小一样的圆形玻璃.
10. B
【解析】如图所示,连接 ,,作 , 的中垂线,交点 就是圆心.
连接 ,,
,,,
.
故选B.
11. D
【解析】A选项,不能确定,因为半径不确定,故不符合题意;
B选项,不能确定,因为圆心的位置不确定,故不符合题意;
C选项,不能确定,因为三点的位置关系不确定,若三点在同一直线上,则无法确定一个圆,故不符合题意;
D选项,不在同一直线上的三点可以确定一个圆,故符合题意.
12. C
13. B
【解析】连接 ,,,,,,.
,,,,
点 到 的三个顶点的距离相等,即点 是 的外心.
14. 无数,不确定,无数,两点所连线段的垂直平分线上,不在同一条直线上
15.
【解析】由题意,得:,,
是等边 的外接圆,
,,,
在 中,
16.
【解析】设直线 的解析式为 ,
,,
解得
,
解方程组 得
当点 的坐标为 时,过 ,, 三点不能作出一个圆.
17.
18. 或 或
19.
【解析】 的外接圆圆心是 各边上线段垂直平分线的交点,线段 的垂直平分线的解析式是 .线段 的垂直平分线的解析式是 ,这两条直线的交点是 ,于是点 坐标是 .
20. 图略;外心分别在锐角三角形的内部,直角三角形斜边上的中点,钝角三角形的外部.
21. 如图,符合条件的圆能作两个.
22. 作图略.第一个锐角三角形的外心在三角形的内部,第二个直角三角形的外心是斜边上的中点,第三个钝角三角形的外心在三角形的外部.
23. 如图,
作线段 的垂直平分线 与弧 交于点 ,连接 ,作线段 的垂直平分线与 交于点 .点 即为圆心.
24. (1) 当直线 与线段 斜交时,直线 与线段 的垂直平分线只有一个交点,
可作 个圆.
(2) 当直线 与线段 垂直,但不经过 的中点时,直线 与线段 的垂直平分线没有交点,
可作 个圆.
(3) 当直线 是线段 的垂直平分线时,可作无数个圆.
25. (1) 如图所示, 即为所求作;
(2)
一、选择题(共13小题)
1. 下列说法正确的是
A. 长度相等的弧叫等弧
B. 平分弦的直径一定垂直于该弦
C. 三角形的外心是三条角平分线的交点
D. 不在同一直线上的三个点确定一个圆
2. 三角形的外心是
A. 三条中线的交点 B. 三条边的中垂线的交点
C. 三条高的交点 D. 三条角平分线的交点
3. 下列说法不正确的是
A. 过一点可作无数个圆,那是因为圆心不确定,半径也不确定
B. 过两个点可以画无数个圆,圆心在这两点连线的中垂线上
C. 过不在同一直线上的三个点只能画一个圆
D. 经过三个点一定可以作圆
4. 已知:在 中,.求作: 的外心 .以下是甲、乙两名同学的作法:
甲:如图(),
①作 的垂直平分线 ;
②作 的垂直平分线 ;
③ , 交于点 ,则点 即为所求.
乙:如图(),
①作 的垂直平分线 ;
②作 的平分线 ;
③ , 交于点 ,则点 即为所求.
两人的作法正确的是
A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
5. 确定一个圆的条件是
A. 已知圆心 B. 已知半径
C. 过三个已知点 D. 过一个三角形的三个顶点
6. 已知内接于 的等边三角形 , 的半径为 ,则这个等边三角形的边长是
A. B. C. D.
7. 现有如下 个命题:
①过两点可以作无数个圆;
②三点可以确定一个圆;
③任意一个三角形有且只有一个外接圆;
④任意一个圆有且只有一个内接三角形.
其中正确的有
A. 个 B. 个 C. 个 D. 个
8. 欢欢不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,欢欢带到商店去的一块玻璃碎片应该是
A. 第①块 B. 第②块 C. 第③块 D. 第④块
9. 小明家的圆形玻璃打碎了,其中三块碎片如图所示,为了配到与原来大小一样的圆形玻璃,小明应带到商店去的一块碎片是
A. ① B. ② C. ③ D. 均不可能
10. 小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形的边长为 )所示的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是
A. B. C. D.
11. 给定下列条件可以确定一个圆的是
A. 已知圆心 B. 已知半径
C. 已知三点 D. 不在同一直线上的三点
12. 如图,已知平面直角坐标系内三点 ,,, 经过点 ,,,则点 的坐标为
A. B. C. D.
13. 如图,在网格(每个小正方形的边长均为 )中选取 个格点(格线的交点称为格点),分别为点 ,,,,,,,,任意连接除点 外的 个格点组成三角形,则组成的三角形中以点 为外心的是
A. B. C. D.
二、填空题(共6小题)
14. 经过一个点的圆有 个,圆心 ;经过两点的圆有 个,圆心在 ;如果平面上的三个点能够确定一个圆,那么这三点所满足的条件是 .
15. 正三角形的边长为 ,那么它的外接圆半径是 .
16. 已知直线 ,点 ,点 ,设点 为直线 上一动点,当点 的坐标为 时,过 ,, 三点不能作出一个圆.
17. 如图,在直角坐标系中,以点 为圆心的圆弧与 轴交于 , 两点,已知 和 ,则点 的坐标是 .
18. 平面上有不在同一直线上的 个点,过其中 个点作圆,可以作出 个圆,则 的值为 .
19. 如图,在平面直角坐标系 中,点 ,, 的坐标分别是 ,,, 是 的外接圆,则点 的坐标为 .
三、解答题(共6小题)
20. 图中的三个三角形从左至右依次为锐角三角形、直角三角形、钝角三角形,分别作出它们的外接圆(不写作法),并说出这些三角形外心的位置有怎样的特点.
21. 如图,已知 和点 ,求作一个圆,使它过点 和 ,且圆心在 的边上,这样的圆能作几个
22. 图中的三个三角形从左至右依次为锐角三角形、直角三角形、钝角三角形,分别作出它们的外接圆(不写作法),并说出这些三角形外心的位置有怎样的特点.
23. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道需确定管道圆形截面的圆心和半径,如图是水平放置的破裂管道的截面.请用无刻度的直尺和圆规作图,确定圆心 的位置(保留作图痕迹).
24. 经过已知两点 , 作圆,并且使圆心在已知直线 上.
(1)当直线 与线段 斜交时,可作几个圆
(2)当直线 与线段 垂直,但不经过 的中点时,可作几个圆
(3)当直线 是线段 的垂直平分线时,可作几个圆
25. 如图,等边三角形 的边长为 .
(1)尺规作图作它的外接圆 ;
(2)则 的半径为 .
答案
1. D
【解析】A.能够完全重合的弧叫等弧,所以 A 选项错误;
B.平分弦(非直径)的直径一定垂直于该弦,所以 B 选项错误;
C.三角形的外心是三边垂直平分线的交点,所以 C 选项错误;
D.不在同一直线上的三个点确定一个圆,所以 D 选项正确.
2. B
3. D
4. A
【解析】甲的作法是作三角形两边的垂直平分线,则点 到三角形三个顶点的距离相等,
所以点 为 的外心;
在乙的作法中,
因为 ,
所以作 的平分线即作 边的垂直平分线,则点 到三角形三个顶点的距离相等,
所以点 为 的外心.
所以两人都对.
5. D
【解析】确定一个圆的条件是已知圆心和半径,过一个三角形的三个顶点即可确定一个圆.
6. C
7. B
【解析】①过两点可以作无数个圆,是真命题.
②不在同一直线上的三点可以确定一个圆,是假命题.
③任意一个三角形有且只有一个外接圆,是真命题.
④任意一个圆有无数个内接三角形,是假命题.
8. B
9. A
【解析】碎片①中有不在同一条直线上的三点在圆形玻璃上,可以确定一个圆,即可以配到与原来大小一样的圆形玻璃.
10. B
【解析】如图所示,连接 ,,作 , 的中垂线,交点 就是圆心.
连接 ,,
,,,
.
故选B.
11. D
【解析】A选项,不能确定,因为半径不确定,故不符合题意;
B选项,不能确定,因为圆心的位置不确定,故不符合题意;
C选项,不能确定,因为三点的位置关系不确定,若三点在同一直线上,则无法确定一个圆,故不符合题意;
D选项,不在同一直线上的三点可以确定一个圆,故符合题意.
12. C
13. B
【解析】连接 ,,,,,,.
,,,,
点 到 的三个顶点的距离相等,即点 是 的外心.
14. 无数,不确定,无数,两点所连线段的垂直平分线上,不在同一条直线上
15.
【解析】由题意,得:,,
是等边 的外接圆,
,,,
在 中,
16.
【解析】设直线 的解析式为 ,
,,
解得
,
解方程组 得
当点 的坐标为 时,过 ,, 三点不能作出一个圆.
17.
18. 或 或
19.
【解析】 的外接圆圆心是 各边上线段垂直平分线的交点,线段 的垂直平分线的解析式是 .线段 的垂直平分线的解析式是 ,这两条直线的交点是 ,于是点 坐标是 .
20. 图略;外心分别在锐角三角形的内部,直角三角形斜边上的中点,钝角三角形的外部.
21. 如图,符合条件的圆能作两个.
22. 作图略.第一个锐角三角形的外心在三角形的内部,第二个直角三角形的外心是斜边上的中点,第三个钝角三角形的外心在三角形的外部.
23. 如图,
作线段 的垂直平分线 与弧 交于点 ,连接 ,作线段 的垂直平分线与 交于点 .点 即为圆心.
24. (1) 当直线 与线段 斜交时,直线 与线段 的垂直平分线只有一个交点,
可作 个圆.
(2) 当直线 与线段 垂直,但不经过 的中点时,直线 与线段 的垂直平分线没有交点,
可作 个圆.
(3) 当直线 是线段 的垂直平分线时,可作无数个圆.
25. (1) 如图所示, 即为所求作;
(2)
