2022-2023学年北师大版九年级数学上册 4.6 利用相似三角形测高 同步练习 (Word版,含解析)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册 4.6 利用相似三角形测高 同步练习 (Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 665.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 14:42:34 | ||
图片预览



文档简介
北师大版 4.6 利用相似三角形测高
一、选择题(共11小题)
1. 如图,有左、右并排的两棵树 和 ,小树 的高 ,大树 的高 ,小明估计自己眼睛距地面的高度 ,当他站在 点时恰好看到大树顶端 点.已知此时他与小树的距离 ,则两棵树之间的距离 是
A. B. C. D.
2. 如图所示的是测量旗杆的高度的方法,已知 是标杆,线段 表示 在太阳光下的影子, 为旗杆,线段 表示 在太阳光下的影子,下列选项叙述错误的是
A. 太阳光线是平行光线
B.
C. 只需量出 和 的长,就可以计算出旗杆的高
D. 量出 ,, 的长,可以计算出旗杆的高
3. 圆桌面(桌面中间有一个直径为 的圆洞)正上方的灯泡(看作一个点)发出的光线照射在平行于地面的桌面上,在地面上形成如图所示的圆环形阴影.已知桌面的直径为 ,桌面离地面 ,若灯泡离地面 ,则地面圆环形阴影的面积是
A. B. C. D.
4. 如图,, 两地之间有一池塘,为测量 , 两地之间的距离,在地面上选择一点 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 .测得 , 间的距离为 米,则 , 两地之间的距离为
A. 米 B. 米 C. 米 D. 米
5. 如图,铁道口的栏杆短臂长 ,长臂长 .当短臂端点下降 时,长臂端点升高
A. B. C. D.
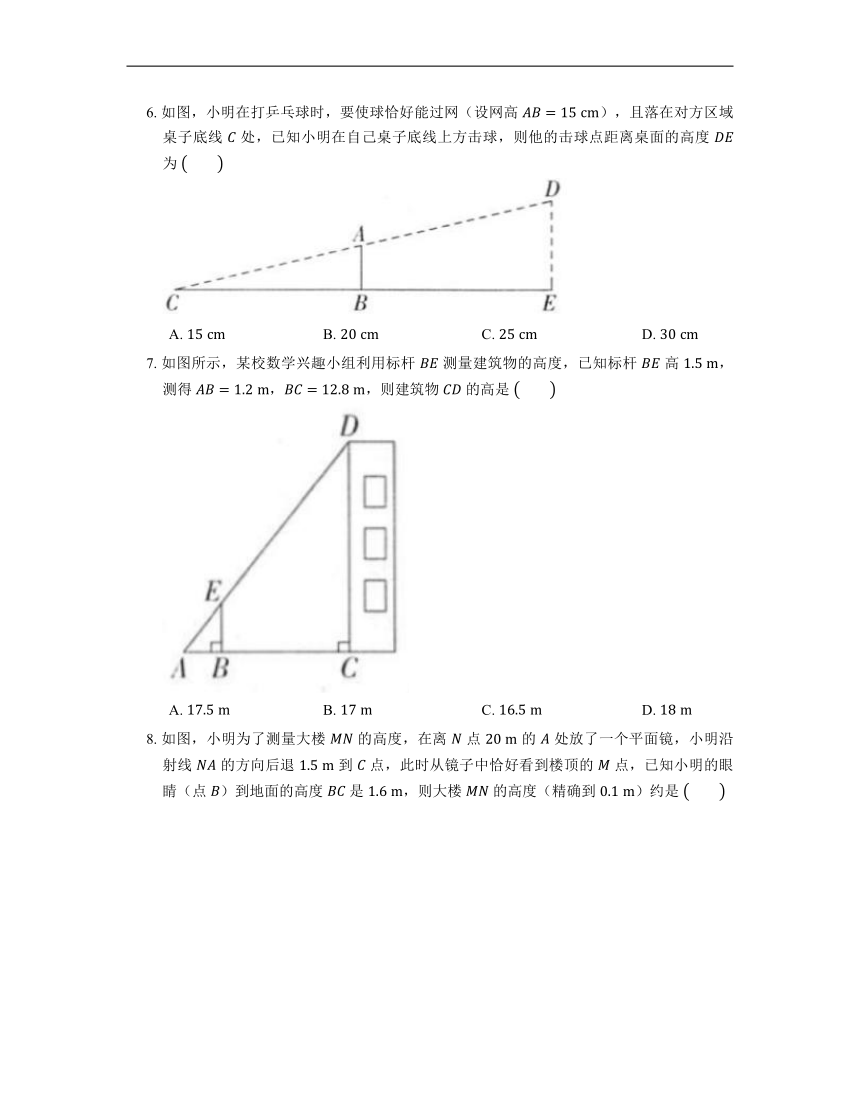
6. 如图,小明在打乒乓球时,要使球恰好能过网(设网高 ),且落在对方区域桌子底线 处,已知小明在自己桌子底线上方击球,则他的击球点距离桌面的高度 为
A. B. C. D.
7. 如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 ,,则建筑物 的高是
A. B. C. D.
8. 如图,小明为了测量大楼 的高度,在离 点 的 处放了一个平面镜,小明沿射线 的方向后退 到 点,此时从镜子中恰好看到楼顶的 点,已知小明的眼睛(点 )到地面的高度 是 ,则大楼 的高度(精确到 )约是
A. B. C. D.
9. 如图,小明为了测量一凉亭的高度 (顶端 到水平地面 的距离),在凉亭的旁边放置一个与凉亭台阶 等高的平台 ( 米,,, 三点共线),把一面镜子水平放置在平台上的点 处,测得 米,然后沿着直线 后退到点 处,这时恰好在镜子里看到凉亭的顶端 ,测得 米,小明身高 米,则凉亭的高度 约为
A. 米 B. 米 C. 米 D. 米
10. 如图, 是斜靠在墙上的长梯,梯脚 距离墙角 ,梯上点 距墙 , 长 ,则梯子长为
A. B. C. D.
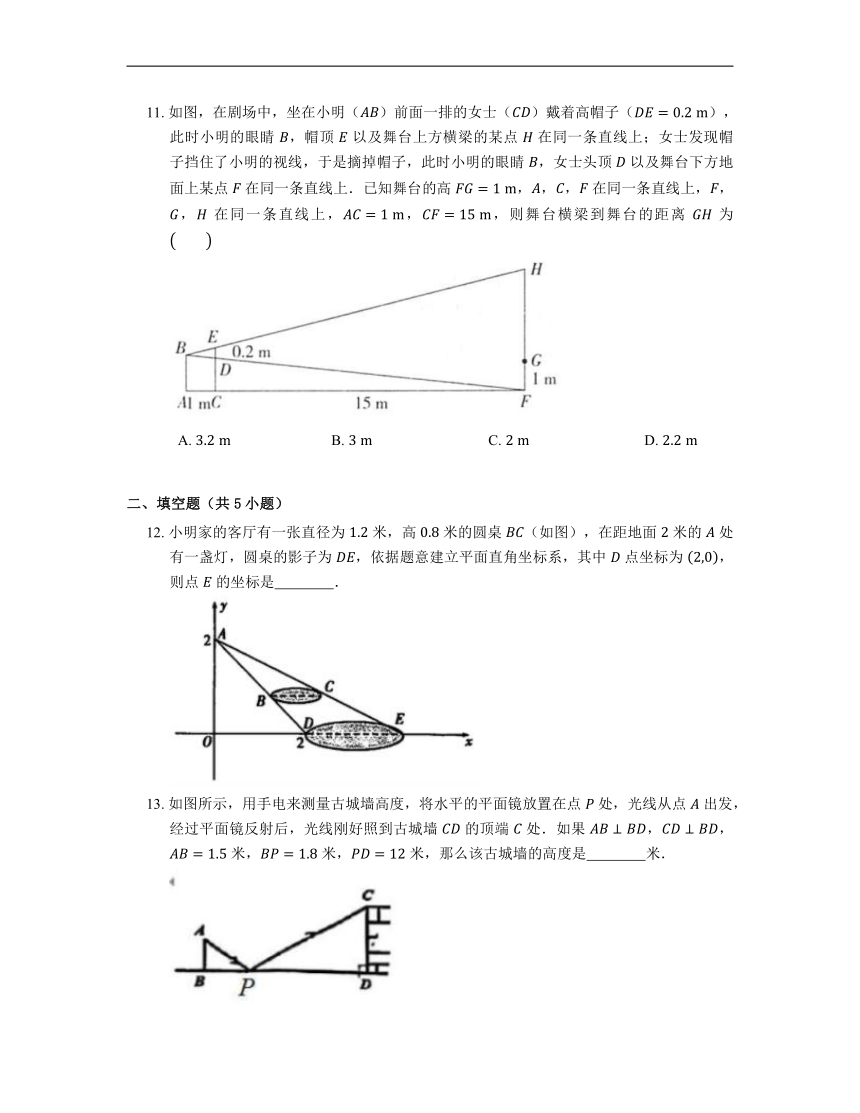
11. 如图,在剧场中,坐在小明()前面一排的女士()戴着高帽子(),此时小明的眼睛 ,帽顶 以及舞台上方横梁的某点 在同一条直线上;女士发现帽子挡住了小明的视线,于是摘掉帽子,此时小明的眼睛 ,女士头顶 以及舞台下方地面上某点 在同一条直线上.已知舞台的高 ,,, 在同一条直线上,,, 在同一条直线上,,,则舞台横梁到舞台的距离 为
A. B. C. D.
二、填空题(共5小题)
12. 小明家的客厅有一张直径为 米,高 米的圆桌 (如图),在距地面 米的 处有一盏灯,圆桌的影子为 ,依据题意建立平面直角坐标系,其中 点坐标为 ,则点 的坐标是 .
13. 如图所示,用手电来测量古城墙高度,将水平的平面镜放置在点 处,光线从点 出发,经过平面镜反射后,光线刚好照到古城墙 的顶端 处.如果 ,, 米, 米, 米,那么该古城墙的高度是 米.
14. 在某一时刻,直立地面的一根竹竿的影长为 米,一根旗杆的影长为 米,已知这根竹竿的长度为 米,那么这根旗杆的高度为 米.
15. 如图所示,用手电来测量古城墙高度,将水平的平面镜放置在点 处,光线从点 出发,经过平面镜反射后,光线刚好照到古城墙 的顶端 处.如果 ,, 米, 米, 米,那么该古城墙的高度是 米.
16. 如图,小芸用灯泡 照射一个矩形相框 ,在墙上形成矩形影子 .现测得 ,,相框 的面积为 ,则影子 的面积为 .
三、解答题(共6小题)
17. 如图,一位同学想利用树影测量树高(),他在某一时刻测得高为 的竹竿影长为 ,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分落在墙上(),他先测得墙上的影高()为 ,又测得地面部分的影长()为 ,试问树有多高
18. 下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
19. 如图,为了测量一栋楼的高度 ,小明同学先在操场上的 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ,再将镜子放到 处,后退到 处,恰好再次在镜子中看到楼的顶部 (,,,, 在同一条直线上),测得 ,,小明的眼睛距地面的高度 , 为 ,试确定楼的高度 .
20. 如图所示,小华在测量电线杆 的高度时,发现电线杆的影子恰好落在坡面 与地面 上,影子 ,, 与地面成 角,且此时测得 长的标杆的影长为 ,求电线杆的高度(结果精确到 , 取 , 取 ).
21. 如图, 是斜靠在墙壁上的长梯,梯脚 距墙 ,梯上一点 距墙 , 长 ,求梯子的长.
22. 如图所示,平台 上有一棵直立的大树 ,平台的边缘 处有一棵直立的小树 ,平台边缘 外有一个向下的斜坡 .小明想利用数学课上学习的知识测量大树 的高度.一天,他发现大树的影子一部分落在平台 上,一部分落在斜坡上,而且大树的顶端 与小树顶端 的影子恰好重合,且都落在斜坡上的 处,经测量, 长 米, 长 米,小树 高 米,斜坡 与平台 所成的角 .请你帮小明求出大树 的高度.
答案
1. B
【解析】由题意,得 ,,
,,
,,
,
,
,
,即 ,解得 .
则 .故选B.
2. C
【解析】由太阳光线是平行光线,可得 ,
又 ,
,
,
,
即已知 ,, 的长,可以计算出旗杆的高,故 A,B,D中叙述正确,不符合题意;
C中,只量出 和 的长,不知道 的长,不能求出旗杆的高,故C中叙述错误,符合题意.
3. D
【解析】如图所示,
,,
,
,
,即 ,
,
同理,由 ,得 ,
.
故选D.
4. C
【解析】 在 和 中,,
且 ,
,
,
又 米,
米.
5. D
【解析】设长臂端点升高 ,则利用相似三角形的知识可得 ,解得 .
故选D.
6. D
【解析】,
,
,
又由题意知 ,
.
7. A
【解析】,,
,
,
.
,,,
,,
解得 .
故选A.
8. C
【解析】,,
.
,
,
,即 ,
,
即大楼 的高度约为 .
9. A
【解析】由光线反射可知 ,
又 ,
,
,
,
米.
米,
米.
10. C
【解析】,,
,
,
,即 ,解得 .
11. D
【解析】由题意知,,, 都垂直于地面 ,
,
,
.
,
,
.
,,,,
,
,
.
12.
【解析】,
,
,
米,
米,
.
13.
【解析】 入射角 反射角,
入射角的余角 反射角的余角 ,
又 ;,
,
,
.
故答案为:.
14.
15.
16.
【解析】由题意可知 ,
,
矩形 的面积:矩形 的面积 ,
又矩形 的面积为 ,则矩形 的面积为 .
17. 如图,延长 ,,交于点 ,
设 ,,
因为某一时刻测得长为 的竹竿影长为 ,墙上的影高 为 ,
所以 ,
解得 ,
所以树的影长为 ,
所以 ,
解得 .
答:树高为 米.
18. 由题意,得 ,
则 ,
即 ,解得 .
答:小河的宽度为 .
19. 如图,设 关于 的对称点为 ,延长 与 ,易知 , 的延长线相交于点 ,连接 并延长,交 于点 .
易知 ,
,
,
,
,
.
答:楼的高度 为 .
20. 延长 交 的延长线于点 ,过点 作 于点 ,如图.
在 中,
因为 ,,
所以 ,
所以 .
由同一时刻物高与影长成比例,得 .
所以 ,.
所以 .
则 .
所以电线杆的高度约是 .
21. 由已知,,
.
.
又 ,
,
即 .
.
梯子的长为 .
22. 如图所示,延长 交 于点 ,过点 作 的延长线于点 .
,,
,
.
的长为 米,
米, 米.
,,
,
,
.
又 米,
,
,
,
,
.
,
,
,
大树 的高度为 米.
一、选择题(共11小题)
1. 如图,有左、右并排的两棵树 和 ,小树 的高 ,大树 的高 ,小明估计自己眼睛距地面的高度 ,当他站在 点时恰好看到大树顶端 点.已知此时他与小树的距离 ,则两棵树之间的距离 是
A. B. C. D.
2. 如图所示的是测量旗杆的高度的方法,已知 是标杆,线段 表示 在太阳光下的影子, 为旗杆,线段 表示 在太阳光下的影子,下列选项叙述错误的是
A. 太阳光线是平行光线
B.
C. 只需量出 和 的长,就可以计算出旗杆的高
D. 量出 ,, 的长,可以计算出旗杆的高
3. 圆桌面(桌面中间有一个直径为 的圆洞)正上方的灯泡(看作一个点)发出的光线照射在平行于地面的桌面上,在地面上形成如图所示的圆环形阴影.已知桌面的直径为 ,桌面离地面 ,若灯泡离地面 ,则地面圆环形阴影的面积是
A. B. C. D.
4. 如图,, 两地之间有一池塘,为测量 , 两地之间的距离,在地面上选择一点 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 .测得 , 间的距离为 米,则 , 两地之间的距离为
A. 米 B. 米 C. 米 D. 米
5. 如图,铁道口的栏杆短臂长 ,长臂长 .当短臂端点下降 时,长臂端点升高
A. B. C. D.
6. 如图,小明在打乒乓球时,要使球恰好能过网(设网高 ),且落在对方区域桌子底线 处,已知小明在自己桌子底线上方击球,则他的击球点距离桌面的高度 为
A. B. C. D.
7. 如图所示,某校数学兴趣小组利用标杆 测量建筑物的高度,已知标杆 高 ,测得 ,,则建筑物 的高是
A. B. C. D.
8. 如图,小明为了测量大楼 的高度,在离 点 的 处放了一个平面镜,小明沿射线 的方向后退 到 点,此时从镜子中恰好看到楼顶的 点,已知小明的眼睛(点 )到地面的高度 是 ,则大楼 的高度(精确到 )约是
A. B. C. D.
9. 如图,小明为了测量一凉亭的高度 (顶端 到水平地面 的距离),在凉亭的旁边放置一个与凉亭台阶 等高的平台 ( 米,,, 三点共线),把一面镜子水平放置在平台上的点 处,测得 米,然后沿着直线 后退到点 处,这时恰好在镜子里看到凉亭的顶端 ,测得 米,小明身高 米,则凉亭的高度 约为
A. 米 B. 米 C. 米 D. 米
10. 如图, 是斜靠在墙上的长梯,梯脚 距离墙角 ,梯上点 距墙 , 长 ,则梯子长为
A. B. C. D.
11. 如图,在剧场中,坐在小明()前面一排的女士()戴着高帽子(),此时小明的眼睛 ,帽顶 以及舞台上方横梁的某点 在同一条直线上;女士发现帽子挡住了小明的视线,于是摘掉帽子,此时小明的眼睛 ,女士头顶 以及舞台下方地面上某点 在同一条直线上.已知舞台的高 ,,, 在同一条直线上,,, 在同一条直线上,,,则舞台横梁到舞台的距离 为
A. B. C. D.
二、填空题(共5小题)
12. 小明家的客厅有一张直径为 米,高 米的圆桌 (如图),在距地面 米的 处有一盏灯,圆桌的影子为 ,依据题意建立平面直角坐标系,其中 点坐标为 ,则点 的坐标是 .
13. 如图所示,用手电来测量古城墙高度,将水平的平面镜放置在点 处,光线从点 出发,经过平面镜反射后,光线刚好照到古城墙 的顶端 处.如果 ,, 米, 米, 米,那么该古城墙的高度是 米.
14. 在某一时刻,直立地面的一根竹竿的影长为 米,一根旗杆的影长为 米,已知这根竹竿的长度为 米,那么这根旗杆的高度为 米.
15. 如图所示,用手电来测量古城墙高度,将水平的平面镜放置在点 处,光线从点 出发,经过平面镜反射后,光线刚好照到古城墙 的顶端 处.如果 ,, 米, 米, 米,那么该古城墙的高度是 米.
16. 如图,小芸用灯泡 照射一个矩形相框 ,在墙上形成矩形影子 .现测得 ,,相框 的面积为 ,则影子 的面积为 .
三、解答题(共6小题)
17. 如图,一位同学想利用树影测量树高(),他在某一时刻测得高为 的竹竿影长为 ,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分落在墙上(),他先测得墙上的影高()为 ,又测得地面部分的影长()为 ,试问树有多高
18. 下表是小明填写的实践活动报告的部分内容,请你借助小明的测量数据,计算小河的宽度.
19. 如图,为了测量一栋楼的高度 ,小明同学先在操场上的 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ,再将镜子放到 处,后退到 处,恰好再次在镜子中看到楼的顶部 (,,,, 在同一条直线上),测得 ,,小明的眼睛距地面的高度 , 为 ,试确定楼的高度 .
20. 如图所示,小华在测量电线杆 的高度时,发现电线杆的影子恰好落在坡面 与地面 上,影子 ,, 与地面成 角,且此时测得 长的标杆的影长为 ,求电线杆的高度(结果精确到 , 取 , 取 ).
21. 如图, 是斜靠在墙壁上的长梯,梯脚 距墙 ,梯上一点 距墙 , 长 ,求梯子的长.
22. 如图所示,平台 上有一棵直立的大树 ,平台的边缘 处有一棵直立的小树 ,平台边缘 外有一个向下的斜坡 .小明想利用数学课上学习的知识测量大树 的高度.一天,他发现大树的影子一部分落在平台 上,一部分落在斜坡上,而且大树的顶端 与小树顶端 的影子恰好重合,且都落在斜坡上的 处,经测量, 长 米, 长 米,小树 高 米,斜坡 与平台 所成的角 .请你帮小明求出大树 的高度.
答案
1. B
【解析】由题意,得 ,,
,,
,,
,
,
,
,即 ,解得 .
则 .故选B.
2. C
【解析】由太阳光线是平行光线,可得 ,
又 ,
,
,
,
即已知 ,, 的长,可以计算出旗杆的高,故 A,B,D中叙述正确,不符合题意;
C中,只量出 和 的长,不知道 的长,不能求出旗杆的高,故C中叙述错误,符合题意.
3. D
【解析】如图所示,
,,
,
,
,即 ,
,
同理,由 ,得 ,
.
故选D.
4. C
【解析】 在 和 中,,
且 ,
,
,
又 米,
米.
5. D
【解析】设长臂端点升高 ,则利用相似三角形的知识可得 ,解得 .
故选D.
6. D
【解析】,
,
,
又由题意知 ,
.
7. A
【解析】,,
,
,
.
,,,
,,
解得 .
故选A.
8. C
【解析】,,
.
,
,
,即 ,
,
即大楼 的高度约为 .
9. A
【解析】由光线反射可知 ,
又 ,
,
,
,
米.
米,
米.
10. C
【解析】,,
,
,
,即 ,解得 .
11. D
【解析】由题意知,,, 都垂直于地面 ,
,
,
.
,
,
.
,,,,
,
,
.
12.
【解析】,
,
,
米,
米,
.
13.
【解析】 入射角 反射角,
入射角的余角 反射角的余角 ,
又 ;,
,
,
.
故答案为:.
14.
15.
16.
【解析】由题意可知 ,
,
矩形 的面积:矩形 的面积 ,
又矩形 的面积为 ,则矩形 的面积为 .
17. 如图,延长 ,,交于点 ,
设 ,,
因为某一时刻测得长为 的竹竿影长为 ,墙上的影高 为 ,
所以 ,
解得 ,
所以树的影长为 ,
所以 ,
解得 .
答:树高为 米.
18. 由题意,得 ,
则 ,
即 ,解得 .
答:小河的宽度为 .
19. 如图,设 关于 的对称点为 ,延长 与 ,易知 , 的延长线相交于点 ,连接 并延长,交 于点 .
易知 ,
,
,
,
,
.
答:楼的高度 为 .
20. 延长 交 的延长线于点 ,过点 作 于点 ,如图.
在 中,
因为 ,,
所以 ,
所以 .
由同一时刻物高与影长成比例,得 .
所以 ,.
所以 .
则 .
所以电线杆的高度约是 .
21. 由已知,,
.
.
又 ,
,
即 .
.
梯子的长为 .
22. 如图所示,延长 交 于点 ,过点 作 的延长线于点 .
,,
,
.
的长为 米,
米, 米.
,,
,
,
.
又 米,
,
,
,
,
.
,
,
,
大树 的高度为 米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
