2022-2023学年北师大版九年级数学上册 6.3 反比例函数的应用同步练习(Word版,含解析)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册 6.3 反比例函数的应用同步练习(Word版,含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 482.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览


文档简介
北师大版 6.3 反比例函数的应用
一、选择题(共11小题)
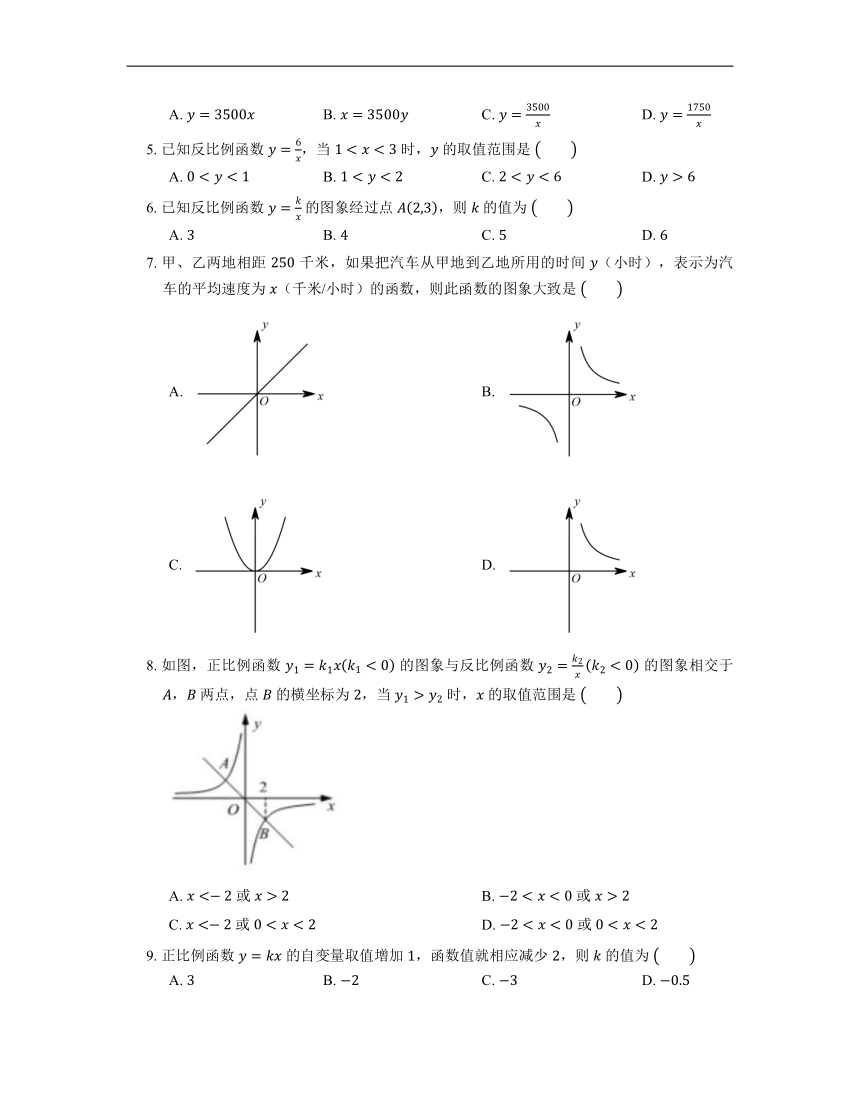
1. 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 是气球体积 的反比例函数,其图象如图所示,当气球内的气压大于 时,气球将爆炸,为了安全,气球的体积应该
A. 不小于 B. 小于 C. 不大于 D. 小于
2. 如图,正比例函数 的图象与反比例函数 的图象相交于 , 两点,其中点 的横坐标为 ,当 时, 的取值范围是
A. B.
C. D.
3. 公元前 世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力 阻力臂 动力 动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力 (单位:)关于动力臂 (单位:)的函数表达式正确的是
A. B. C. D.
4. 某小区要种植一个面积为 的矩形草坪,已知草坪的长 随宽 的变化而变化,可用函数的解析式表示为
A. B. C. D.
5. 已知反比例函数 ,当 时, 的取值范围是
A. B. C. D.
6. 已知反比例函数 的图象经过点 ,则 的值为
A. B. C. D.
7. 甲、乙两地相距 千米,如果把汽车从甲地到乙地所用的时间 (小时),表示为汽车的平均速度为 (千米/小时)的函数,则此函数的图象大致是
A. B.
C. D.
8. 如图,正比例函数 的图象与反比例函数 的图象相交于 , 两点,点 的横坐标为 ,当 时, 的取值范围是
A. 或 B. 或
C. 或 D. 或
9. 正比例函数 的自变量取值增加 ,函数值就相应减少 ,则 的值为
A. B. C. D.
10. 在化学课上,老师教同学们配制烧碱溶液,已知有烧碱 ,则溶液的浓度 (单位:)与加水后溶液体积 (单位:)间的函数关系的图象大致是
A. B.
C. D.
11. 如图所示,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 的取值范围是
A. 或 B. 或
C. 或 D. 或
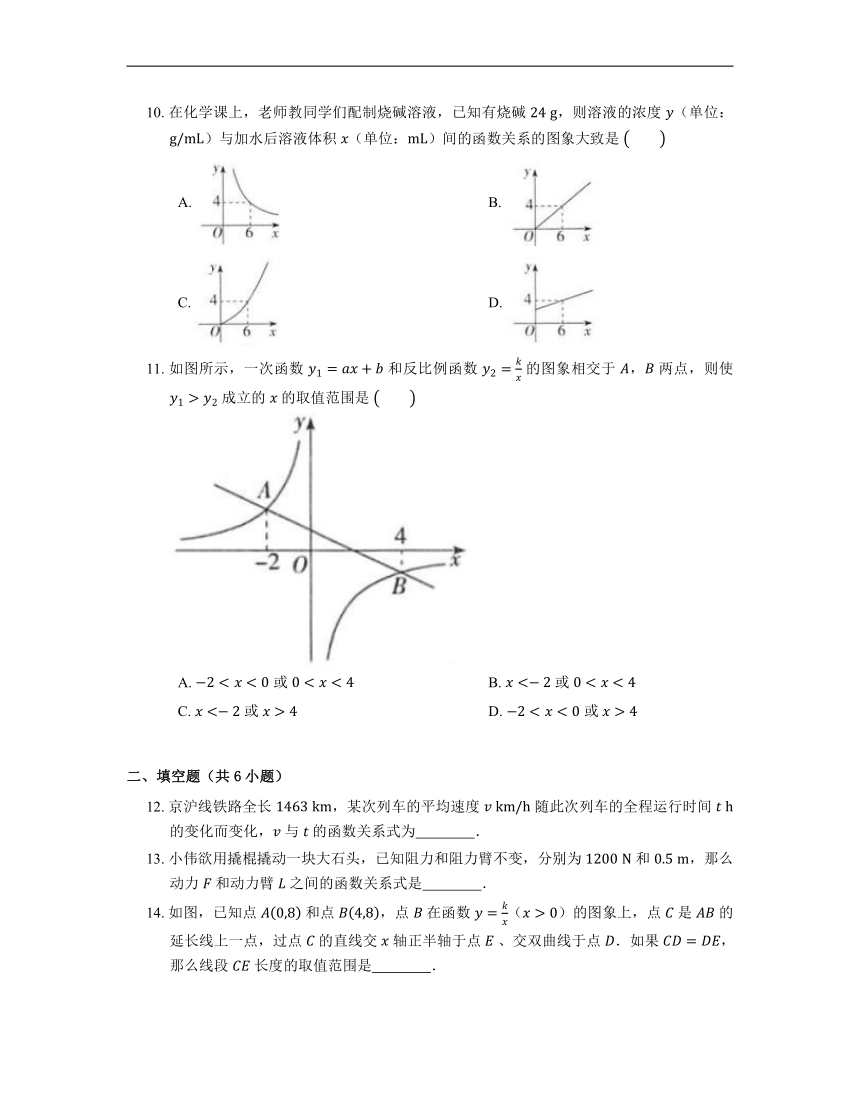
二、填空题(共6小题)
12. 京沪线铁路全长 ,某次列车的平均速度 随此次列车的全程运行时间 的变化而变化, 与 的函数关系式为 .
13. 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为 和 ,那么动力 和动力臂 之间的函数关系式是 .
14. 如图,已知点 和点 ,点 在函数 ()的图象上,点 是 的延长线上一点,过点 的直线交 轴正半轴于点 、交双曲线于点 .如果 ,那么线段 长度的取值范围是 .
15. 已知点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,若反比例函数图象经过点 ,则该反比例函数的解析式为 .
16. 如图,在平面直角坐标系中,已知点 的坐标为 ,射线 与反比例函数 的图象交于点 ,过点 作 轴的垂线交双曲线于点 ,过点 作 轴的垂线交双曲线于点 ,连接 ,,那么 的值是 .
17. 定义:如果一个 与 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是 与 的“反比例平移函数”.
例如: 的图象向左平移 个单位,再向下平移 个单位得到 的图象,则 是 与 的“反比例平移函数”.如图,在平面直角坐标系中,点 为原点,矩形 的顶点 , 的坐标分别为 ,.点 是 的中点,连接 , 交于点 ,“反比例平移函数” 的图象经过 , 两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,则这个反比例函数的表达式为 .
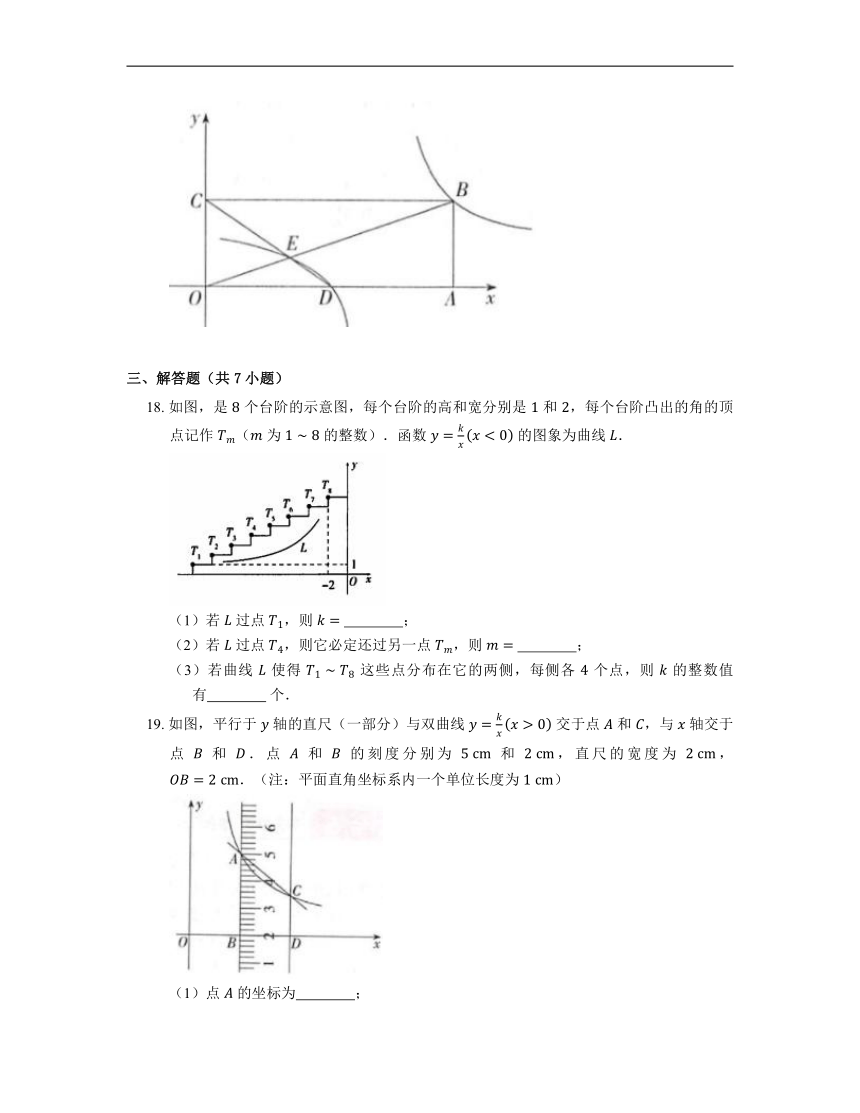
三、解答题(共7小题)
18. 如图,是 个台阶的示意图,每个台阶的高和宽分别是 和 ,每个台阶凸出的角的顶点记作 ( 为 的整数).函数 的图象为曲线 .
(1)若 过点 ,则 ;
(2)若 过点 ,则它必定还过另一点 ,则 ;
(3)若曲线 使得 这些点分布在它的两侧,每侧各 个点,则 的整数值有 个.
19. 如图,平行于 轴的直尺(一部分)与双曲线 交于点 和 ,与 轴交于点 和 .点 和 的刻度分别为 和 ,直尺的宽度为 ,.(注:平面直角坐标系内一个单位长度为 )
(1)点 的坐标为 ;
(2)求双曲线 的解析式;
(3)若经过 , 两点的直线解析式为 ,请直接写出关于 的不等式 的解集.
20. 年春节高速免费时间: 年 月 日 时— 年 月 日 时,共 天.王明从河南信阳老家驾车返回距离 千米的北京上班,假设高速公路全程限速 千米/小时,设小汽车的行驶时间为 (单位:小时),行驶平均速度为 (单位:千米/小时).
(1)求 关于 的函数表达式;
(2)春节假期最后一天是返程高峰,王明预计高速公路会出现拥堵,估计小汽车的行驶速度不超过 千米/小时,王明若下午 点出发,能否在高速免费截止时间( 月 日 时)前下高速
21. 如图,已知一次函数 的图象与反比例函数 的图象交于 , 两点.
(1)请直接写出不等式 的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点 作 轴的垂线,垂足为 ,连接 ,求 的面积.
22. 已知:如图,在平面直角坐标系 中,直线 与 轴交于点 ,在第一象限内与反比例函数图象交于点 , 垂直于 轴,垂足为点 ,且 .求
(1)点 的坐标;
(2)反比例函数的解析式.
23. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
(1)求一次函数和反比例函数的解析式;
(2)点 在 轴上,且满足 的面积等于 ,请直接写出点 的坐标.
24. 如图,已知 , 是一次函数 的图象和反比例函数 的图象的两个交点.
(1)求反比例函数和一次函数的解析式.
(2)求直线 与 轴的交点 的坐标及 的面积.
(3)方程 的解是 .
(4)不等式 的解集是 .
答案
1. A
【解析】设气球内气体的气压 和气体体积 的关系式为 ,
因为图象过点 ,
所以 ,即 ,
当 时,,
因为在第一象限内, 随 的增大而减小,
所以当 时,.
2. D
3. B
【解析】因为阻力 阻力臂 动力 动力臂,
所以 ,
所以 .
4. C
5. C
6. D
【解析】 反比例函数 的图象经过点 ,
.
7. D
8. C
【解析】由反比例函数与正比例函数相交于点 ,,可得点 坐标与点 坐标关于原点对称.
故点 的横坐标为 .
当 时,即正比例函数图象在反比例图象上方,
观察图象可得,当 或 时满足题意.
9. B
【解析】根据题意得 ,
即 ,
而 ,
.
故选:B.
10. A
【解析】依题意,得 ,即 ,
函数图象为双曲线在第一象限的部分.故选A.
11. B
【解析】观察函数图象可发现:当 或 时,一次函数图象在反比例函数图象上方,
所以使 成立的 的取值范围是 或 .
12.
13.
14.
【解析】
,
,
当 ,,
当 ,,
.
15.
【解析】因为点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,
所以 点坐标为: 或 ,
设反比例函数的解析式为 ,
所以 ,
则该反比例函数的解析式为:.
16.
17. ,
【解析】由题意易得 ,,把 和 的坐标代入 ,
得 解得
则“反比例平移函数”的表达式为 .
,易知所求的反比例函数的表达式为 .
18. (1)
【解析】因为每个台阶的高和宽分别是 和 , 的纵坐标为 , 的横坐标为 ,所以 的坐标为 , 的坐标为 , 的坐标为 .
若 过点 ,则 .
(2)
【解析】若 过点 ,则 ,
因为 ,所以 过点 ,则 .
(3)
【解析】当 时, 经过点 和 ,当 时, 经过点 和 ,显然若曲线 使得 这些点分布在它的两侧,每侧各 个点,一定是点 ,,, 在曲线上方,其余四个点在曲线下方,点 的坐标为 若 过点 ,则 ;点 的坐标为 ,若 过点 ,则 .所以满足题意的 的取值范围为 ,故 的整数值有 个.
19. (1)
(2) 将 点坐标代入 中,
得 ,
,
双曲线的解析式为 .
(3) 直尺的宽度为 ,
,
,
点 的横坐标为 .
由图象可知,
关于 的不等式 的解集是 或 .
20. (1) ,
关于 的函数表达式为 ().
(2) 把 代入 得 ,所以王明至少在中午 点开始从老家出发,才能在高速免费截止时间前下高速,所以王明若从下午 点出发,不能在高速免费截止时间前下高速.
21. (1) 由图象可知,不等式 的解集为 或 .
(2) 因为一次函数 的图象与反比例函数 的图象交于 , 两点,
所以 ,,
解得 ,,,
所以反比例函数和一次函数的解析式分别为 ,.
(3) .
22. (1) 对于直线 ,当 时,得 ,
解得 .
直线 与 轴的交点 的坐标为 .
.
,
.
点 的坐标为 .
(2) 垂直于 轴,
,
,
,
,
设反比例函数的解析式:,
把点 代入得 ,
反比例函数的解析式:.
23. (1) 由题意可得:
点 在反比例函数 图象上,
,则 ,
反比例函数的解析式为 ,
将 代入 ,
得:,即 ,
将 , 代入一次函数解析式中,得 解得:
一次函数解析式为 .
(2) 或
【解析】 点 在 轴上,
设点 的坐标为 ,
一次函数解析式为 ,令 ,则 ,
直线 与 轴交于点 ,
由 的面积为 ,可得:
,即 ,
解得: 或 ,
点 的坐标为 或 .
24. (1) ,.
(2) ,.
(3) ,
(4) 或
一、选择题(共11小题)
1. 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 是气球体积 的反比例函数,其图象如图所示,当气球内的气压大于 时,气球将爆炸,为了安全,气球的体积应该
A. 不小于 B. 小于 C. 不大于 D. 小于
2. 如图,正比例函数 的图象与反比例函数 的图象相交于 , 两点,其中点 的横坐标为 ,当 时, 的取值范围是
A. B.
C. D.
3. 公元前 世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力 阻力臂 动力 动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是 和 ,则动力 (单位:)关于动力臂 (单位:)的函数表达式正确的是
A. B. C. D.
4. 某小区要种植一个面积为 的矩形草坪,已知草坪的长 随宽 的变化而变化,可用函数的解析式表示为
A. B. C. D.
5. 已知反比例函数 ,当 时, 的取值范围是
A. B. C. D.
6. 已知反比例函数 的图象经过点 ,则 的值为
A. B. C. D.
7. 甲、乙两地相距 千米,如果把汽车从甲地到乙地所用的时间 (小时),表示为汽车的平均速度为 (千米/小时)的函数,则此函数的图象大致是
A. B.
C. D.
8. 如图,正比例函数 的图象与反比例函数 的图象相交于 , 两点,点 的横坐标为 ,当 时, 的取值范围是
A. 或 B. 或
C. 或 D. 或
9. 正比例函数 的自变量取值增加 ,函数值就相应减少 ,则 的值为
A. B. C. D.
10. 在化学课上,老师教同学们配制烧碱溶液,已知有烧碱 ,则溶液的浓度 (单位:)与加水后溶液体积 (单位:)间的函数关系的图象大致是
A. B.
C. D.
11. 如图所示,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 的取值范围是
A. 或 B. 或
C. 或 D. 或
二、填空题(共6小题)
12. 京沪线铁路全长 ,某次列车的平均速度 随此次列车的全程运行时间 的变化而变化, 与 的函数关系式为 .
13. 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为 和 ,那么动力 和动力臂 之间的函数关系式是 .
14. 如图,已知点 和点 ,点 在函数 ()的图象上,点 是 的延长线上一点,过点 的直线交 轴正半轴于点 、交双曲线于点 .如果 ,那么线段 长度的取值范围是 .
15. 已知点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,若反比例函数图象经过点 ,则该反比例函数的解析式为 .
16. 如图,在平面直角坐标系中,已知点 的坐标为 ,射线 与反比例函数 的图象交于点 ,过点 作 轴的垂线交双曲线于点 ,过点 作 轴的垂线交双曲线于点 ,连接 ,,那么 的值是 .
17. 定义:如果一个 与 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是 与 的“反比例平移函数”.
例如: 的图象向左平移 个单位,再向下平移 个单位得到 的图象,则 是 与 的“反比例平移函数”.如图,在平面直角坐标系中,点 为原点,矩形 的顶点 , 的坐标分别为 ,.点 是 的中点,连接 , 交于点 ,“反比例平移函数” 的图象经过 , 两点,则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,则这个反比例函数的表达式为 .
三、解答题(共7小题)
18. 如图,是 个台阶的示意图,每个台阶的高和宽分别是 和 ,每个台阶凸出的角的顶点记作 ( 为 的整数).函数 的图象为曲线 .
(1)若 过点 ,则 ;
(2)若 过点 ,则它必定还过另一点 ,则 ;
(3)若曲线 使得 这些点分布在它的两侧,每侧各 个点,则 的整数值有 个.
19. 如图,平行于 轴的直尺(一部分)与双曲线 交于点 和 ,与 轴交于点 和 .点 和 的刻度分别为 和 ,直尺的宽度为 ,.(注:平面直角坐标系内一个单位长度为 )
(1)点 的坐标为 ;
(2)求双曲线 的解析式;
(3)若经过 , 两点的直线解析式为 ,请直接写出关于 的不等式 的解集.
20. 年春节高速免费时间: 年 月 日 时— 年 月 日 时,共 天.王明从河南信阳老家驾车返回距离 千米的北京上班,假设高速公路全程限速 千米/小时,设小汽车的行驶时间为 (单位:小时),行驶平均速度为 (单位:千米/小时).
(1)求 关于 的函数表达式;
(2)春节假期最后一天是返程高峰,王明预计高速公路会出现拥堵,估计小汽车的行驶速度不超过 千米/小时,王明若下午 点出发,能否在高速免费截止时间( 月 日 时)前下高速
21. 如图,已知一次函数 的图象与反比例函数 的图象交于 , 两点.
(1)请直接写出不等式 的解集;
(2)求反比例函数和一次函数的解析式;
(3)过点 作 轴的垂线,垂足为 ,连接 ,求 的面积.
22. 已知:如图,在平面直角坐标系 中,直线 与 轴交于点 ,在第一象限内与反比例函数图象交于点 , 垂直于 轴,垂足为点 ,且 .求
(1)点 的坐标;
(2)反比例函数的解析式.
23. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
(1)求一次函数和反比例函数的解析式;
(2)点 在 轴上,且满足 的面积等于 ,请直接写出点 的坐标.
24. 如图,已知 , 是一次函数 的图象和反比例函数 的图象的两个交点.
(1)求反比例函数和一次函数的解析式.
(2)求直线 与 轴的交点 的坐标及 的面积.
(3)方程 的解是 .
(4)不等式 的解集是 .
答案
1. A
【解析】设气球内气体的气压 和气体体积 的关系式为 ,
因为图象过点 ,
所以 ,即 ,
当 时,,
因为在第一象限内, 随 的增大而减小,
所以当 时,.
2. D
3. B
【解析】因为阻力 阻力臂 动力 动力臂,
所以 ,
所以 .
4. C
5. C
6. D
【解析】 反比例函数 的图象经过点 ,
.
7. D
8. C
【解析】由反比例函数与正比例函数相交于点 ,,可得点 坐标与点 坐标关于原点对称.
故点 的横坐标为 .
当 时,即正比例函数图象在反比例图象上方,
观察图象可得,当 或 时满足题意.
9. B
【解析】根据题意得 ,
即 ,
而 ,
.
故选:B.
10. A
【解析】依题意,得 ,即 ,
函数图象为双曲线在第一象限的部分.故选A.
11. B
【解析】观察函数图象可发现:当 或 时,一次函数图象在反比例函数图象上方,
所以使 成立的 的取值范围是 或 .
12.
13.
14.
【解析】
,
,
当 ,,
当 ,,
.
15.
【解析】因为点 位于第三象限内,且点 到两坐标轴的距离分别为 和 ,
所以 点坐标为: 或 ,
设反比例函数的解析式为 ,
所以 ,
则该反比例函数的解析式为:.
16.
17. ,
【解析】由题意易得 ,,把 和 的坐标代入 ,
得 解得
则“反比例平移函数”的表达式为 .
,易知所求的反比例函数的表达式为 .
18. (1)
【解析】因为每个台阶的高和宽分别是 和 , 的纵坐标为 , 的横坐标为 ,所以 的坐标为 , 的坐标为 , 的坐标为 .
若 过点 ,则 .
(2)
【解析】若 过点 ,则 ,
因为 ,所以 过点 ,则 .
(3)
【解析】当 时, 经过点 和 ,当 时, 经过点 和 ,显然若曲线 使得 这些点分布在它的两侧,每侧各 个点,一定是点 ,,, 在曲线上方,其余四个点在曲线下方,点 的坐标为 若 过点 ,则 ;点 的坐标为 ,若 过点 ,则 .所以满足题意的 的取值范围为 ,故 的整数值有 个.
19. (1)
(2) 将 点坐标代入 中,
得 ,
,
双曲线的解析式为 .
(3) 直尺的宽度为 ,
,
,
点 的横坐标为 .
由图象可知,
关于 的不等式 的解集是 或 .
20. (1) ,
关于 的函数表达式为 ().
(2) 把 代入 得 ,所以王明至少在中午 点开始从老家出发,才能在高速免费截止时间前下高速,所以王明若从下午 点出发,不能在高速免费截止时间前下高速.
21. (1) 由图象可知,不等式 的解集为 或 .
(2) 因为一次函数 的图象与反比例函数 的图象交于 , 两点,
所以 ,,
解得 ,,,
所以反比例函数和一次函数的解析式分别为 ,.
(3) .
22. (1) 对于直线 ,当 时,得 ,
解得 .
直线 与 轴的交点 的坐标为 .
.
,
.
点 的坐标为 .
(2) 垂直于 轴,
,
,
,
,
设反比例函数的解析式:,
把点 代入得 ,
反比例函数的解析式:.
23. (1) 由题意可得:
点 在反比例函数 图象上,
,则 ,
反比例函数的解析式为 ,
将 代入 ,
得:,即 ,
将 , 代入一次函数解析式中,得 解得:
一次函数解析式为 .
(2) 或
【解析】 点 在 轴上,
设点 的坐标为 ,
一次函数解析式为 ,令 ,则 ,
直线 与 轴交于点 ,
由 的面积为 ,可得:
,即 ,
解得: 或 ,
点 的坐标为 或 .
24. (1) ,.
(2) ,.
(3) ,
(4) 或
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
