2022-2023年吉林省长春市榆树市八号镇第一中学 华东师大版九年级数学上册 23.2相似图形课堂练习(Word版,含答案)
文档属性
| 名称 | 2022-2023年吉林省长春市榆树市八号镇第一中学 华东师大版九年级数学上册 23.2相似图形课堂练习(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 14:54:13 | ||
图片预览



文档简介
23.2相似图形课堂练习---吉林省榆树市八号镇第一中学2022-2023学年华东师大版九年级数学上册
一.选择题
1.下列说法中,不正确的是( )
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正八边形都相似
2.形状相同的图形是相似图形.下列哪组图形不一定是相似图形( )
A.关于直线对称的两个图形
B.两个正三角形
C.两个等腰三角形
D.两个半径不等的圆
3.甲说:将三角形各边向内平移1个单位并适当缩短,得到如图1所示的图形,变化前后的两个三角形相似.
乙说:将矩形(长和宽不相等)各边向内平移1个单位并适当缩短,得到如图2所示的图形,变化前后的两个矩形相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.甲对,乙不对 D.甲不对,乙对
4.下列图形中,不是相似图形的一组是( )
A. B.
C. D.
5.下图中是相似图形的一组是( )
A. B.
C. D.
6.下列判断正确的是( )
A.对角线相等的四边形是矩形
B.将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似
C.若点C是AB的黄金分割点,且AB=6cm,则BC的长为(3﹣3)cm
D.如果两个相似三角形的面积比为16:9,那么这两个相似三角形的周长比是4:3
7.下列说法正确的是( )
A.任意两个菱形都相似
B.任意两个正方形都相似
C.任意两个等腰三角形都相似
D.任意两个矩形都相似
8.下列说法正确的是( )
A.有一个角等于100°的两个等腰三角形相似
B.两个矩形一定相似
C.有一个角等于45°的两个等腰三角形相似
D.相似三角形一定不是全等三角形
9.下列图形,一定相似的是( )
A.两个直角三角形 B.两个等腰三角形
C.两个等边三角形 D.两个菱形
10.下列各组图形中,不一定相似的是( )
A.任意两个等腰直角三角形
B.任意两个等边三角形
C.任意两个矩形
D.任意两个正方形
11.如图,四边形ABCD和四边形EFGH相似,且顶点都在方格纸的格点上,它们的相似比是( )
A.1:2 B.1:4 C.2:1 D.4:1
12.两个相似多边形的周长之比为1:4,则它们的面积之比为( )
A.1:2 B.1:4 C.1:8 D.1:16
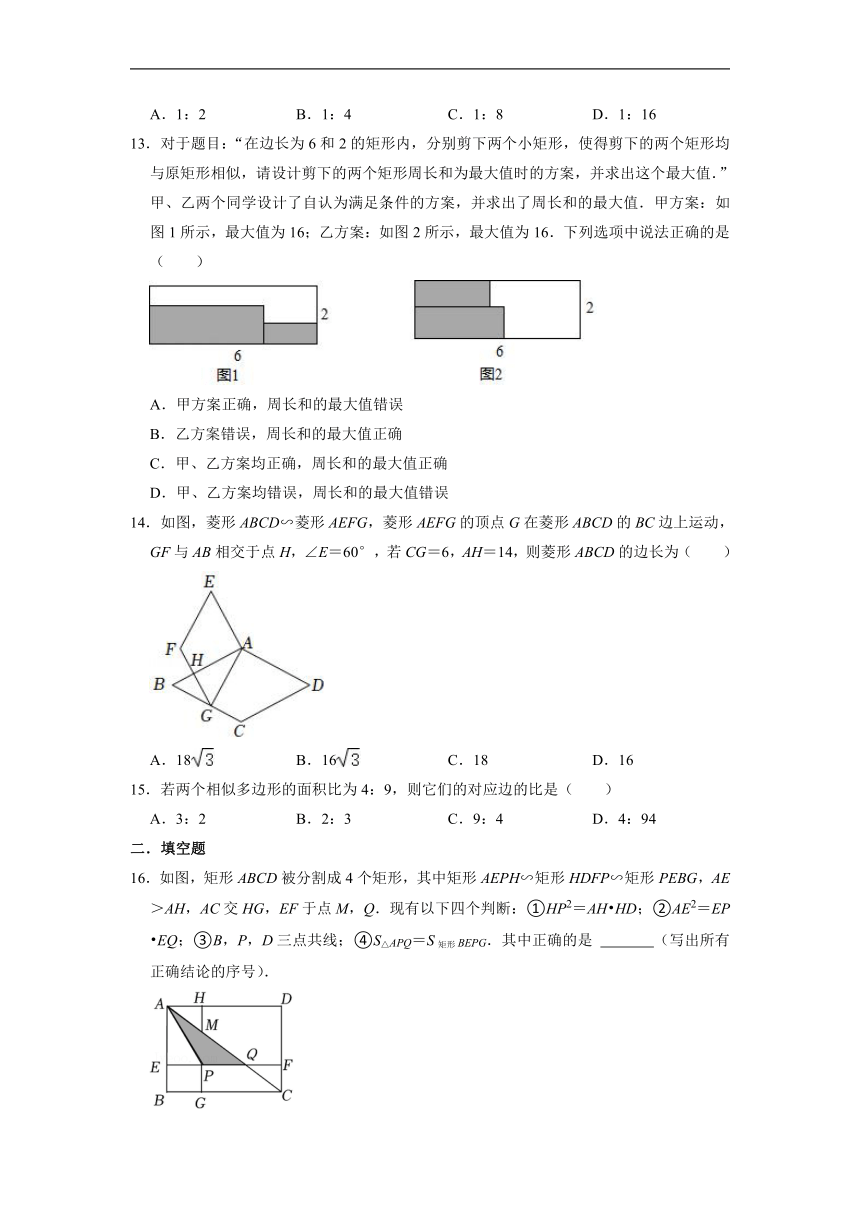
13.对于题目:“在边长为6和2的矩形内,分别剪下两个小矩形,使得剪下的两个矩形均与原矩形相似,请设计剪下的两个矩形周长和为最大值时的方案,并求出这个最大值.”甲、乙两个同学设计了自认为满足条件的方案,并求出了周长和的最大值.甲方案:如图1所示,最大值为16;乙方案:如图2所示,最大值为16.下列选项中说法正确的是( )
A.甲方案正确,周长和的最大值错误
B.乙方案错误,周长和的最大值正确
C.甲、乙方案均正确,周长和的最大值正确
D.甲、乙方案均错误,周长和的最大值错误
14.如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=6,AH=14,则菱形ABCD的边长为( )
A.18 B.16 C.18 D.16
15.若两个相似多边形的面积比为4:9,则它们的对应边的比是( )
A.3:2 B.2:3 C.9:4 D.4:94
二.填空题
16.如图,矩形ABCD被分割成4个矩形,其中矩形AEPH∽矩形HDFP∽矩形PEBG,AE>AH,AC交HG,EF于点M,Q.现有以下四个判断:①HP2=AH HD;②AE2=EP EQ;③B,P,D三点共线;④S△APQ=S矩形BEPG.其中正确的是 (写出所有正确结论的序号).
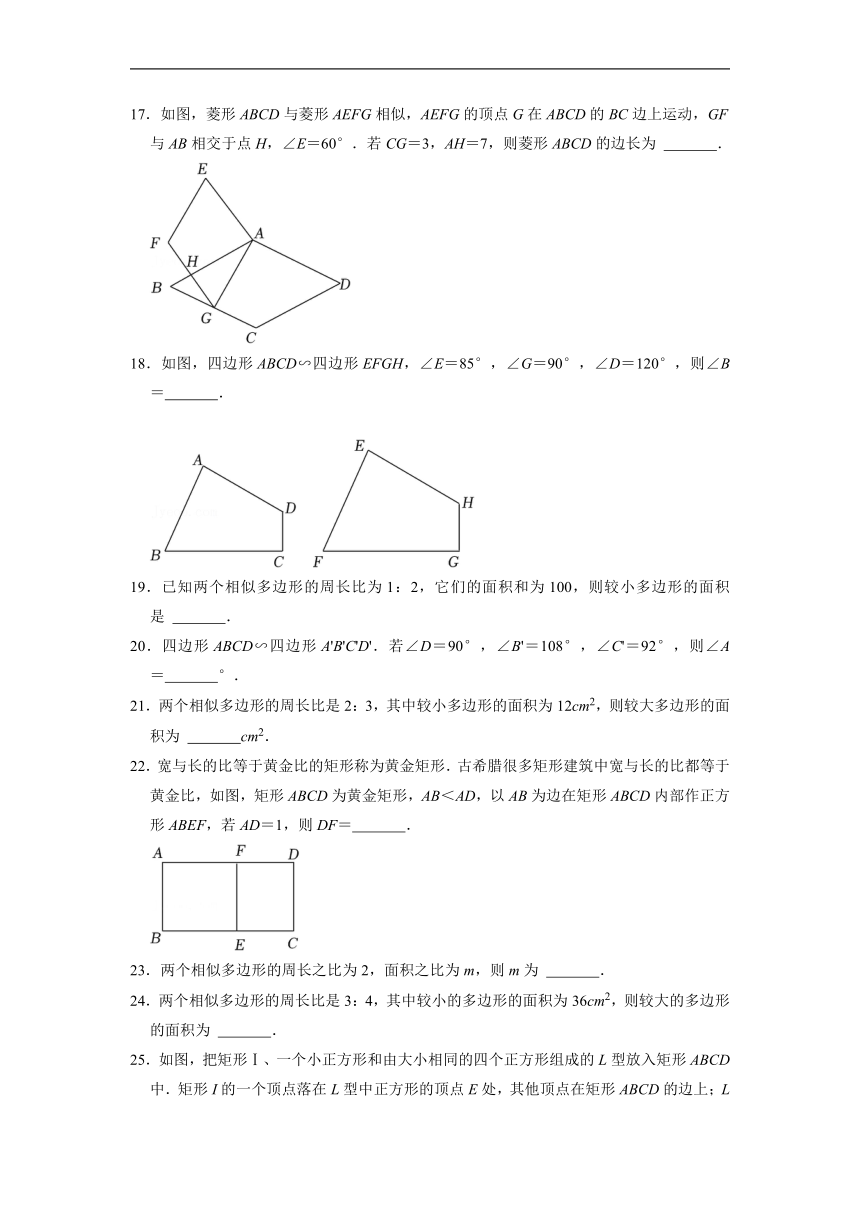
17.如图,菱形ABCD与菱形AEFG相似,AEFG的顶点G在ABCD的BC边上运动,GF与AB相交于点H,∠E=60°.若CG=3,AH=7,则菱形ABCD的边长为 .
18.如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B= .
19.已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 .
20.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= °.
21.两个相似多边形的周长比是2:3,其中较小多边形的面积为12cm2,则较大多边形的面积为 cm2.
22.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD为黄金矩形,AB<AD,以AB为边在矩形ABCD内部作正方形ABEF,若AD=1,则DF= .
23.两个相似多边形的周长之比为2,面积之比为m,则m为 .
24.两个相似多边形的周长比是3:4,其中较小的多边形的面积为36cm2,则较大的多边形的面积为 .
25.如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的L型放入矩形ABCD中.矩形I的一个顶点落在L型中正方形的顶点E处,其他顶点在矩形ABCD的边上;L型中的正方形有三个顶点恰好在矩形ABCD的边上,另有一个顶点和小正方形顶点合.若矩形I与矩形ABCD相似,则AB:BC的值为 .
26.如图,矩形ABCD∽矩形BCEF,若AB=8,BC=6,则CE的值为 .
27.如图,矩形ABCD被分割为5个全等的长方形,若这5个矩形都与矩形ABCD相似,则AD:AB的值是 .
28.已知四边形ABCD与四边形A'B'C′D'相似,边AB与边A'B'是对应边,S四边形ABCD:S四边形A'B′C′D′=2:4,AB=2,则A'B'= .
29.如果两个相似多边形面积的比为25:49,则它们的相似比为 .
30.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
三.解答题
31.如图,一个矩形的长AB=am,宽AD=1m,按照图中所示的方式将它分割成相同的三个矩形,且每个小矩形与原矩形相似,求a的值.
32.如图,四边形ABCD∽四边形A'B'C'D'.
(1)∠B= °.
(2)求边x,y的长度.
33.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
34.已知图中的两个四边形是相似四边形,分别求未知边x的长度和角α的度数.
35.书籍和纸张的长与宽比值都有固定的尺寸,如常用的A3、A4、A5的纸张长与宽的比值都相等.一长方形纸张对折后的小长方形的长与宽的比值与原长方形的长与宽的比值相等.
(1)求满足这样条件的长方形的长与宽的比值;
(2)如图所示的长方形ABCD长与宽之比也满足以上条件,其中宽AB=2.点P是AD上一点,将△BPA沿BP折叠得到△BPE,当BE垂直AC时,求AP的长.
23.2相似图形课堂练习---吉林省榆树市八号镇第一中学2022-2023学年华东师大版九年级数学上册
参考答案
一.选择题
1. C.2. C.3. C.4. D.5. A.6. D.7. B.8. A.9. C.10. C.11. C.12. D.13. C.14. C.15. B.
二.填空题
16.如图,矩形ABCD被分割成4个矩形,其中矩形AEPH∽矩形HDFP∽矩形PEBG,AE>AH,AC交HG,EF于点M,Q.现有以下四个判断:①HP2=AH HD;②AE2=EP EQ;③B,P,D三点共线;④S△APQ=S矩形BEPG.其中正确的是 ①②③ (写出所有正确结论的序号).
17.如图,菱形ABCD与菱形AEFG相似,AEFG的顶点G在ABCD的BC边上运动,GF与AB相交于点H,∠E=60°.若CG=3,AH=7,则菱形ABCD的边长为 9 .
18.如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B= 65° .
19.已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 20 .
20.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= 70 °.
21.两个相似多边形的周长比是2:3,其中较小多边形的面积为12cm2,则较大多边形的面积为 27 cm2.
22.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD为黄金矩形,AB<AD,以AB为边在矩形ABCD内部作正方形ABEF,若AD=1,则DF= .
23.两个相似多边形的周长之比为2,面积之比为m,则m为 4 .
24.两个相似多边形的周长比是3:4,其中较小的多边形的面积为36cm2,则较大的多边形的面积为 64cm2 .
25.如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的L型放入矩形ABCD中.矩形I的一个顶点落在L型中正方形的顶点E处,其他顶点在矩形ABCD的边上;L型中的正方形有三个顶点恰好在矩形ABCD的边上,另有一个顶点和小正方形顶点合.若矩形I与矩形ABCD相似,则AB:BC的值为 或 .
26.如图,矩形ABCD∽矩形BCEF,若AB=8,BC=6,则CE的值为 .
27.如图,矩形ABCD被分割为5个全等的长方形,若这5个矩形都与矩形ABCD相似,则AD:AB的值是 .
28.已知四边形ABCD与四边形A'B'C′D'相似,边AB与边A'B'是对应边,S四边形ABCD:S四边形A'B′C′D′=2:4,AB=2,则A'B'= 2 .
29.如果两个相似多边形面积的比为25:49,则它们的相似比为 5:7 .
30.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
三.解答题
31.
解:∵每个小矩形与原矩形相似,
∴,
解得a=或﹣(舍去),
∴a=.
32.
解:(1)∵四边形ABCD∽四边形A'B'C'D',
∴∠C=∠C'=135°,
∴∠B=360°﹣60°﹣96°﹣135°=69°,
故答案为69°;
(2)∵四边形ABCD∽四边形A'B'C'D',
,
解得x=4,y=18.
33.
(1)解:①四条边成比例的两个凸四边形相似,是假命题,角不一定相等;
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例;
③两个大小不同的正方形相似,是真命题;
故答案为:假,假,真;
(2)证明:如图,连接BD,B1D1.
∵∠BCD=∠B1C1D1,且,
∴△BCD∽△B1C1D1,
∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵,
∴,
∵∠ABC=∠A1B1C1,
∴∠ABD=∠A1B1D1,
∴△ABD∽△A1B1D1,
∴,
∴∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
∴四边形ABCD与四边形A1B1C1D1相似.
34.
解:因为两个四边形是相似四边形,
∴=,
∴x=,α=360°﹣88°﹣96°﹣107°=69°.
35.
解:(1)设长方形的长与宽分别为a,b.
由题意:=,
∴a2=2b2,
∴=.
(2)①如图1中,延长PE、BC交于点G,
∵∠PEB=90°,
∴PE⊥BE,
∵BE⊥AC,BE⊥PE,
∴PG∥AC,
∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=2,AD∥BG,∠ABC=90°,
∴四边形APGC是平行四边形,
∴PG=AC===2,
∵AD∥BC,
∴∠APB=∠GBP,
∵∠APB=∠GPB,
∴∠GBP=∠GPB,
∴GP=GB=2,
∴AP=CG=BG=BC=2﹣2.
一.选择题
1.下列说法中,不正确的是( )
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正八边形都相似
2.形状相同的图形是相似图形.下列哪组图形不一定是相似图形( )
A.关于直线对称的两个图形
B.两个正三角形
C.两个等腰三角形
D.两个半径不等的圆
3.甲说:将三角形各边向内平移1个单位并适当缩短,得到如图1所示的图形,变化前后的两个三角形相似.
乙说:将矩形(长和宽不相等)各边向内平移1个单位并适当缩短,得到如图2所示的图形,变化前后的两个矩形相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对
C.甲对,乙不对 D.甲不对,乙对
4.下列图形中,不是相似图形的一组是( )
A. B.
C. D.
5.下图中是相似图形的一组是( )
A. B.
C. D.
6.下列判断正确的是( )
A.对角线相等的四边形是矩形
B.将一个矩形风景画的四周镶上宽度相等的金边后得到的新矩形与原矩形相似
C.若点C是AB的黄金分割点,且AB=6cm,则BC的长为(3﹣3)cm
D.如果两个相似三角形的面积比为16:9,那么这两个相似三角形的周长比是4:3
7.下列说法正确的是( )
A.任意两个菱形都相似
B.任意两个正方形都相似
C.任意两个等腰三角形都相似
D.任意两个矩形都相似
8.下列说法正确的是( )
A.有一个角等于100°的两个等腰三角形相似
B.两个矩形一定相似
C.有一个角等于45°的两个等腰三角形相似
D.相似三角形一定不是全等三角形
9.下列图形,一定相似的是( )
A.两个直角三角形 B.两个等腰三角形
C.两个等边三角形 D.两个菱形
10.下列各组图形中,不一定相似的是( )
A.任意两个等腰直角三角形
B.任意两个等边三角形
C.任意两个矩形
D.任意两个正方形
11.如图,四边形ABCD和四边形EFGH相似,且顶点都在方格纸的格点上,它们的相似比是( )
A.1:2 B.1:4 C.2:1 D.4:1
12.两个相似多边形的周长之比为1:4,则它们的面积之比为( )
A.1:2 B.1:4 C.1:8 D.1:16
13.对于题目:“在边长为6和2的矩形内,分别剪下两个小矩形,使得剪下的两个矩形均与原矩形相似,请设计剪下的两个矩形周长和为最大值时的方案,并求出这个最大值.”甲、乙两个同学设计了自认为满足条件的方案,并求出了周长和的最大值.甲方案:如图1所示,最大值为16;乙方案:如图2所示,最大值为16.下列选项中说法正确的是( )
A.甲方案正确,周长和的最大值错误
B.乙方案错误,周长和的最大值正确
C.甲、乙方案均正确,周长和的最大值正确
D.甲、乙方案均错误,周长和的最大值错误
14.如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=6,AH=14,则菱形ABCD的边长为( )
A.18 B.16 C.18 D.16
15.若两个相似多边形的面积比为4:9,则它们的对应边的比是( )
A.3:2 B.2:3 C.9:4 D.4:94
二.填空题
16.如图,矩形ABCD被分割成4个矩形,其中矩形AEPH∽矩形HDFP∽矩形PEBG,AE>AH,AC交HG,EF于点M,Q.现有以下四个判断:①HP2=AH HD;②AE2=EP EQ;③B,P,D三点共线;④S△APQ=S矩形BEPG.其中正确的是 (写出所有正确结论的序号).
17.如图,菱形ABCD与菱形AEFG相似,AEFG的顶点G在ABCD的BC边上运动,GF与AB相交于点H,∠E=60°.若CG=3,AH=7,则菱形ABCD的边长为 .
18.如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B= .
19.已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 .
20.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= °.
21.两个相似多边形的周长比是2:3,其中较小多边形的面积为12cm2,则较大多边形的面积为 cm2.
22.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD为黄金矩形,AB<AD,以AB为边在矩形ABCD内部作正方形ABEF,若AD=1,则DF= .
23.两个相似多边形的周长之比为2,面积之比为m,则m为 .
24.两个相似多边形的周长比是3:4,其中较小的多边形的面积为36cm2,则较大的多边形的面积为 .
25.如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的L型放入矩形ABCD中.矩形I的一个顶点落在L型中正方形的顶点E处,其他顶点在矩形ABCD的边上;L型中的正方形有三个顶点恰好在矩形ABCD的边上,另有一个顶点和小正方形顶点合.若矩形I与矩形ABCD相似,则AB:BC的值为 .
26.如图,矩形ABCD∽矩形BCEF,若AB=8,BC=6,则CE的值为 .
27.如图,矩形ABCD被分割为5个全等的长方形,若这5个矩形都与矩形ABCD相似,则AD:AB的值是 .
28.已知四边形ABCD与四边形A'B'C′D'相似,边AB与边A'B'是对应边,S四边形ABCD:S四边形A'B′C′D′=2:4,AB=2,则A'B'= .
29.如果两个相似多边形面积的比为25:49,则它们的相似比为 .
30.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
三.解答题
31.如图,一个矩形的长AB=am,宽AD=1m,按照图中所示的方式将它分割成相同的三个矩形,且每个小矩形与原矩形相似,求a的值.
32.如图,四边形ABCD∽四边形A'B'C'D'.
(1)∠B= °.
(2)求边x,y的长度.
33.根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;( 命题)
②三个角分别相等的两个凸四边形相似;( 命题)
③两个大小不同的正方形相似.( 命题)
(2)如图,在四边形ABCD和四边形A1B1C1D1中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,.求证:四边形ABCD与四边形A1B1C1D1相似.
34.已知图中的两个四边形是相似四边形,分别求未知边x的长度和角α的度数.
35.书籍和纸张的长与宽比值都有固定的尺寸,如常用的A3、A4、A5的纸张长与宽的比值都相等.一长方形纸张对折后的小长方形的长与宽的比值与原长方形的长与宽的比值相等.
(1)求满足这样条件的长方形的长与宽的比值;
(2)如图所示的长方形ABCD长与宽之比也满足以上条件,其中宽AB=2.点P是AD上一点,将△BPA沿BP折叠得到△BPE,当BE垂直AC时,求AP的长.
23.2相似图形课堂练习---吉林省榆树市八号镇第一中学2022-2023学年华东师大版九年级数学上册
参考答案
一.选择题
1. C.2. C.3. C.4. D.5. A.6. D.7. B.8. A.9. C.10. C.11. C.12. D.13. C.14. C.15. B.
二.填空题
16.如图,矩形ABCD被分割成4个矩形,其中矩形AEPH∽矩形HDFP∽矩形PEBG,AE>AH,AC交HG,EF于点M,Q.现有以下四个判断:①HP2=AH HD;②AE2=EP EQ;③B,P,D三点共线;④S△APQ=S矩形BEPG.其中正确的是 ①②③ (写出所有正确结论的序号).
17.如图,菱形ABCD与菱形AEFG相似,AEFG的顶点G在ABCD的BC边上运动,GF与AB相交于点H,∠E=60°.若CG=3,AH=7,则菱形ABCD的边长为 9 .
18.如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B= 65° .
19.已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 20 .
20.四边形ABCD∽四边形A'B'C'D'.若∠D=90°,∠B'=108°,∠C'=92°,则∠A= 70 °.
21.两个相似多边形的周长比是2:3,其中较小多边形的面积为12cm2,则较大多边形的面积为 27 cm2.
22.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD为黄金矩形,AB<AD,以AB为边在矩形ABCD内部作正方形ABEF,若AD=1,则DF= .
23.两个相似多边形的周长之比为2,面积之比为m,则m为 4 .
24.两个相似多边形的周长比是3:4,其中较小的多边形的面积为36cm2,则较大的多边形的面积为 64cm2 .
25.如图,把矩形Ⅰ、一个小正方形和由大小相同的四个正方形组成的L型放入矩形ABCD中.矩形I的一个顶点落在L型中正方形的顶点E处,其他顶点在矩形ABCD的边上;L型中的正方形有三个顶点恰好在矩形ABCD的边上,另有一个顶点和小正方形顶点合.若矩形I与矩形ABCD相似,则AB:BC的值为 或 .
26.如图,矩形ABCD∽矩形BCEF,若AB=8,BC=6,则CE的值为 .
27.如图,矩形ABCD被分割为5个全等的长方形,若这5个矩形都与矩形ABCD相似,则AD:AB的值是 .
28.已知四边形ABCD与四边形A'B'C′D'相似,边AB与边A'B'是对应边,S四边形ABCD:S四边形A'B′C′D′=2:4,AB=2,则A'B'= 2 .
29.如果两个相似多边形面积的比为25:49,则它们的相似比为 5:7 .
30.如图所示的正方形网格中,每个小正方形的边长均为1,四边形ABCD的面积是 .若四边形EFGH与四边形ABCD相似,则四边形EFGH的面积是 .
三.解答题
31.
解:∵每个小矩形与原矩形相似,
∴,
解得a=或﹣(舍去),
∴a=.
32.
解:(1)∵四边形ABCD∽四边形A'B'C'D',
∴∠C=∠C'=135°,
∴∠B=360°﹣60°﹣96°﹣135°=69°,
故答案为69°;
(2)∵四边形ABCD∽四边形A'B'C'D',
,
解得x=4,y=18.
33.
(1)解:①四条边成比例的两个凸四边形相似,是假命题,角不一定相等;
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例;
③两个大小不同的正方形相似,是真命题;
故答案为:假,假,真;
(2)证明:如图,连接BD,B1D1.
∵∠BCD=∠B1C1D1,且,
∴△BCD∽△B1C1D1,
∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵,
∴,
∵∠ABC=∠A1B1C1,
∴∠ABD=∠A1B1D1,
∴△ABD∽△A1B1D1,
∴,
∴∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
∴四边形ABCD与四边形A1B1C1D1相似.
34.
解:因为两个四边形是相似四边形,
∴=,
∴x=,α=360°﹣88°﹣96°﹣107°=69°.
35.
解:(1)设长方形的长与宽分别为a,b.
由题意:=,
∴a2=2b2,
∴=.
(2)①如图1中,延长PE、BC交于点G,
∵∠PEB=90°,
∴PE⊥BE,
∵BE⊥AC,BE⊥PE,
∴PG∥AC,
∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=2,AD∥BG,∠ABC=90°,
∴四边形APGC是平行四边形,
∴PG=AC===2,
∵AD∥BC,
∴∠APB=∠GBP,
∵∠APB=∠GPB,
∴∠GBP=∠GPB,
∴GP=GB=2,
∴AP=CG=BG=BC=2﹣2.
