2022-2023学年吉林省长春市榆树市八号镇第一中学华东师大版九年级数学上册 23.3相似三角形课堂练习(Word版,含答案)
文档属性
| 名称 | 2022-2023学年吉林省长春市榆树市八号镇第一中学华东师大版九年级数学上册 23.3相似三角形课堂练习(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 559.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 14:59:39 | ||
图片预览


文档简介
23.3相似三角形课堂练习---吉林省榆树市八号镇第一中学2022-2023学年华东师大版九年级数学上册
一.选择题
1.两个三角形相似比是2:3,其中小三角形的周长为18,则另一个大三角形的周长是( )
A.12 B.18 C.24 D.27
2.已知两个相似三角形的周长比为2:3,若较大三角形的面积等于18cm2,则较小三角形的面积等于( )
A.8cm2 B.12cm2 C.27cm2 D.40.5cm2
3.已知△ABC∽△DEF,=,若BC=2,则EF=( )
A.4 B.6 C.8 D.16
4.在一张复印出来的纸上,一个三角形的一条边由原图中的2cm增加了4cm,则复印出的三角形的面积是原图中三角形面积的( )
A.4倍 B.6倍 C.9倍 D.12倍
5.如图,在△ABC中,DE∥BC,DE=2,BC=5,则S△ADE:S△ABC的值是( )
A. B. C. D.
6.如图,点D在△ABC的边AC上,添加一个条件,使得△ADB∽△ABC,下列不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
7.如图,D,E是△ABC边上的两个点,请你再添加一个条件,使得△ABC∽△AED,则下列选项不成立的是( )
A.= B.= C.∠C=∠ADE D.∠B=∠AED
8.如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=8,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
A.或 B.10或
C.或10 D.以上答案都不对
9.如图,在正方形网格中有5个格点三角形,分别是:①△ABC,②△ACD,③△ADE,④△AEF,⑤△AGH,其中与⑤相似的三角形是( )
A.①③ B.①④ C.②④ D.①③④
10.如图,在菱形ABCD中,点E在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
A.= B. C.= D.=
11.如图,△ABC中,D是AB边上一点,DE∥BC交AC于点E,连接BE,DF∥BE交AC于点F,则下列结论正确的是( )
A. B. C. D.
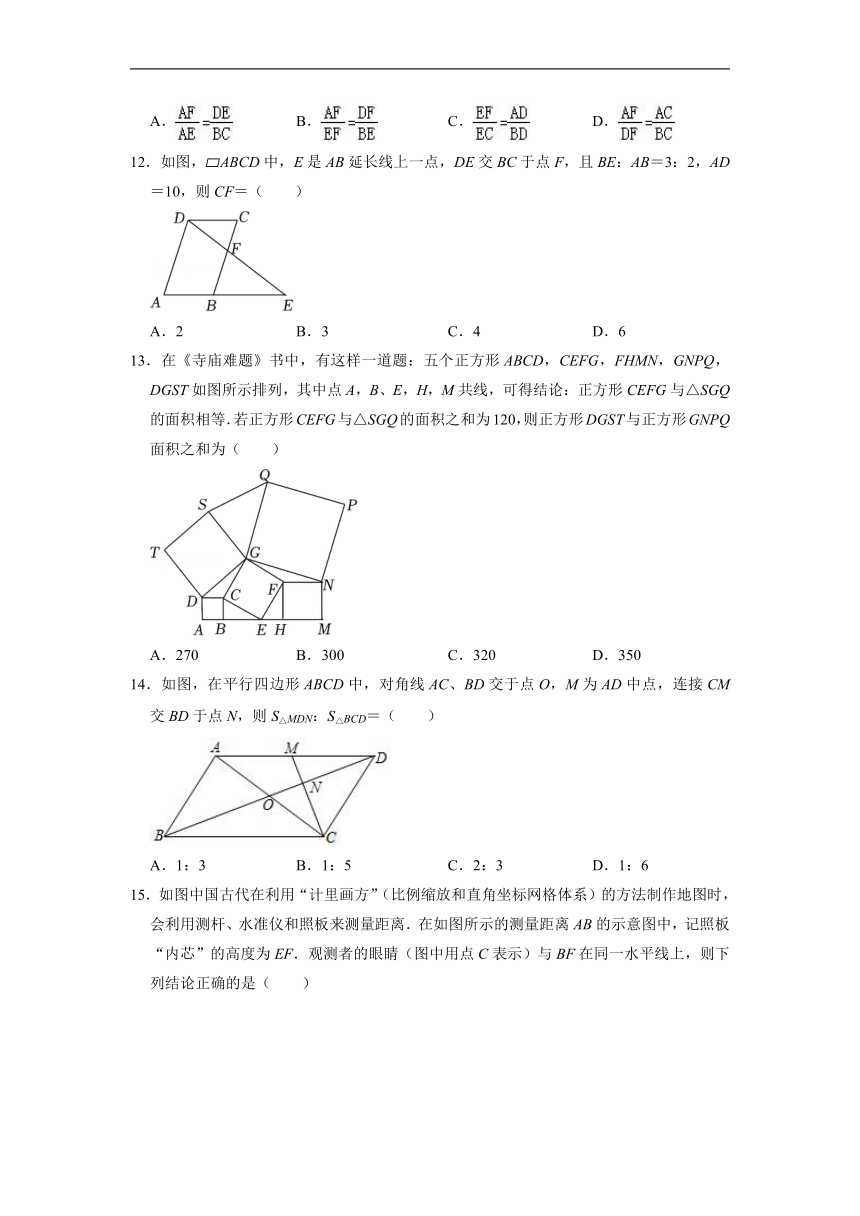
12.如图, ABCD中,E是AB延长线上一点,DE交BC于点F,且BE:AB=3:2,AD=10,则CF=( )
A.2 B.3 C.4 D.6
13.在《寺庙难题》书中,有这样一道题:五个正方形ABCD,CEFG,FHMN,GNPQ,DGST如图所示排列,其中点A,B、E,H,M共线,可得结论:正方形CEFG与△SGQ的面积相等.若正方形CEFG与△SGQ的面积之和为120,则正方形DGST与正方形GNPQ面积之和为( )
A.270 B.300 C.320 D.350
14.如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,则S△MDN:S△BCD=( )
A.1:3 B.1:5 C.2:3 D.1:6
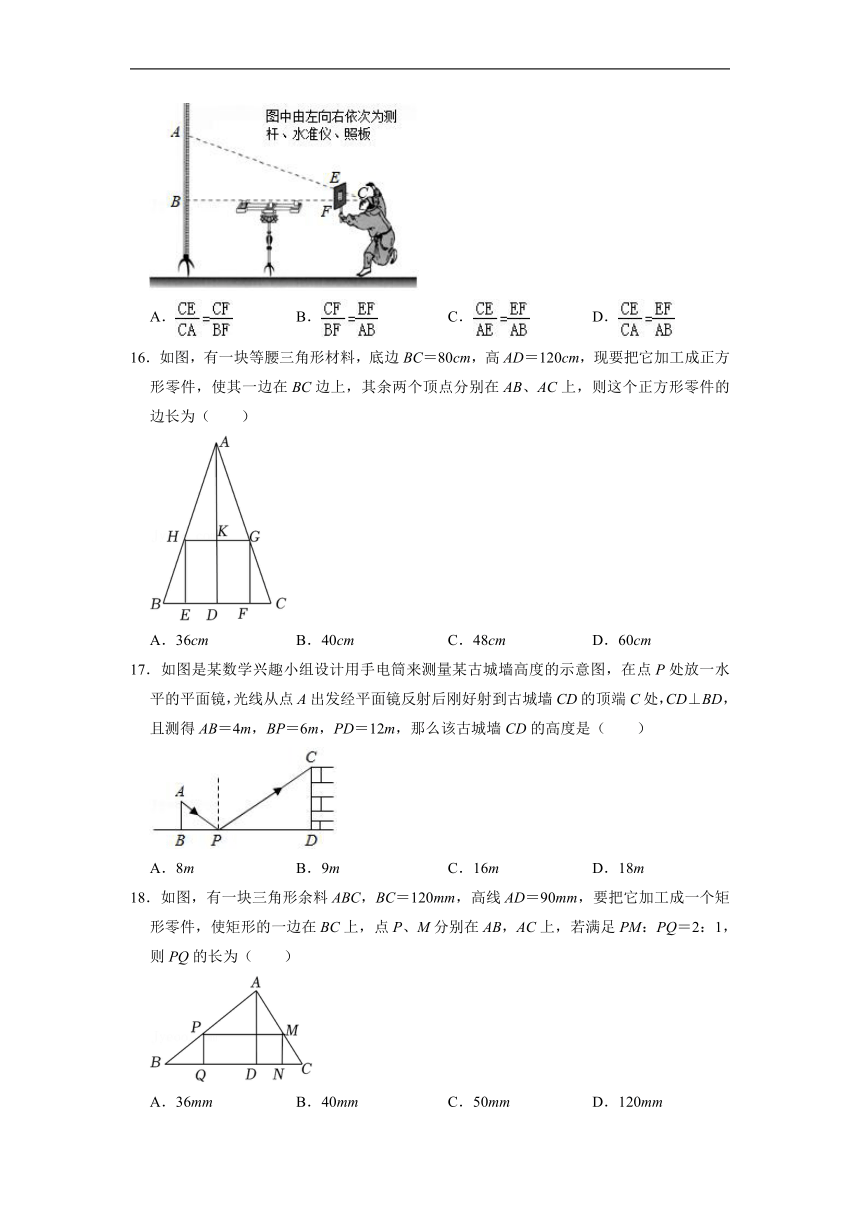
15.如图中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论正确的是( )
A. B. C. D.
16.如图,有一块等腰三角形材料,底边BC=80cm,高AD=120cm,现要把它加工成正方形零件,使其一边在BC边上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为( )
A.36cm B.40cm C.48cm D.60cm
17.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
18.如图,有一块三角形余料ABC,BC=120mm,高线AD=90mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P、M分别在AB,AC上,若满足PM:PQ=2:1,则PQ的长为( )
A.36mm B.40mm C.50mm D.120mm
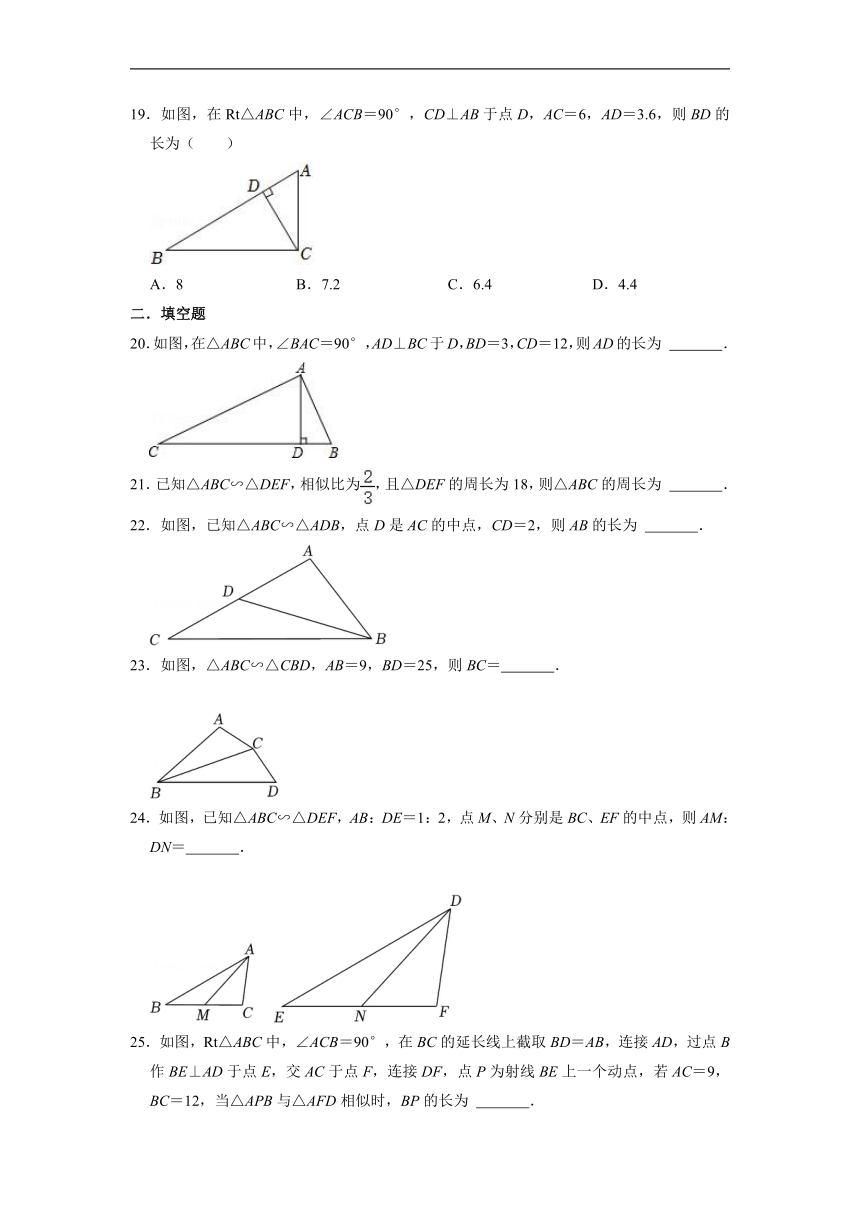
19.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=6,AD=3.6,则BD的长为( )
A.8 B.7.2 C.6.4 D.4.4
二.填空题
20.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 .
21.已知△ABC∽△DEF,相似比为,且△DEF的周长为18,则△ABC的周长为 .
22.如图,已知△ABC∽△ADB,点D是AC的中点,CD=2,则AB的长为 .
23.如图,△ABC∽△CBD,AB=9,BD=25,则BC= .
24.如图,已知△ABC∽△DEF,AB:DE=1:2,点M、N分别是BC、EF的中点,则AM:DN= .
25.如图,Rt△ABC中,∠ACB=90°,在BC的延长线上截取BD=AB,连接AD,过点B作BE⊥AD于点E,交AC于点F,连接DF,点P为射线BE上一个动点,若AC=9,BC=12,当△APB与△AFD相似时,BP的长为 .
26.如图,在正方形网格中有三个三角形,分别是△EBC,△CDB,△DEB,其中与△ABC相似的是 .
27.如图,点P为△ABC的边AB上的一点,添加 ,可以使△ABC与△APC相似.
28.如图,在△ABC中,AB=8cm,AC=16cm,点P从A出发,以2cm/s的速度向B运动,同时点Q从C出发,以3cm/s的速度向A运动,当其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为t.
(1)用含t的代数式表示:AQ= ;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间t= .
29.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=3,BC=4,DF=6,DE=8,判定这两个三角形是否相似. .(填“相似”或“不相似”)
30.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当△APB和△CPD相似时,PD= cm.
31.如图,在正方形ABCD的外侧,以AD为边作等边三角形AED,连接AC交BE于点F,则= .
32.如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F,G,BC=3,AF:FG:GD=3:2:1,则AB的长为 .
33.如图,在△ABC中,AD为∠CAB的平分线,DE∥AB,若DE=3,CE=4,则AB的值 .
34.中国教育家孔子周游列国14年,其中10年居卫(卫国即现在的濮阳),龙湖论语广场有一尊孔子雕像,数学兴趣小组的同学为了测量雕像的高度AB(顶端A到水平地面BE的距离),在雕像旁边的水平地面上C处放了一面镜子(平面镜的厚度忽略不计),组长小丽沿直线BC后退到点E处,这时恰好在镜子里看到雕像的顶端A,此时测得BC=7米,EC=2米,小丽的眼睛距地面的高度DE=1.6米,则雕像的高度AB= 米.
35.如图是步枪在瞄准时的示意图,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,若从眼睛到准星的距离OE为0.5m,则眼睛到目标的距离OF为 m.
三.解答题
36.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是40cm,镜面中心C距离旗杆底部D的距离为5m,如图所示,已知小丽同学的身高是1.66m,眼睛位置A距离小丽头顶的距离是6cm,求出旗杆DE的高度.
37.如图F为平行四边形ABCD的边AB延长线上一点,DF分别交CB、AC于G、E.
(1)求证:;
(2)若EF=16,GE=4,求DE.
38.如图,四边形ABCD为平行四边形,E为边BC上一点,连接BD、AE,它们相交于点F,且∠BDA=∠BAE.
(1)求证:BE2=EF AE;
(2)若BE=4,EF=2,DF=6,求AB的长.
39.如图,在Rt△ABC中,∠ABC=90°,E是边AC上一点,且BE=BC,过点A作BE的垂线,交BE的延长线于点D,求证:△ADE∽△ABC.
40.如图,已知∠B=∠E=90°,AB=6,BF=3,CF=5,DE=15,DF=25.
求证:△ABC∽△DEF.
23.3相似三角形课堂练习---吉林省榆树市八号镇第一中学2022-2023学年华东师大版九年级数学上册
参考答案
一.选择题
1. D.2. A.3. A.4. C.5. B.6. C.7. B.8. C.9. A.10. C.11. A.12. C.13. B.14. D.15. D.16. C.17. A.18. A.19. C.
二.填空题
20.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 6 .
21.已知△ABC∽△DEF,相似比为,且△DEF的周长为18,则△ABC的周长为 12 .
22.如图,已知△ABC∽△ADB,点D是AC的中点,CD=2,则AB的长为 2 .
23.如图,△ABC∽△CBD,AB=9,BD=25,则BC= 15 .
24.如图,已知△ABC∽△DEF,AB:DE=1:2,点M、N分别是BC、EF的中点,则AM:DN= 1:2 .
25.如图,Rt△ABC中,∠ACB=90°,在BC的延长线上截取BD=AB,连接AD,过点B作BE⊥AD于点E,交AC于点F,连接DF,点P为射线BE上一个动点,若AC=9,BC=12,当△APB与△AFD相似时,BP的长为 或9 .
26.如图,在正方形网格中有三个三角形,分别是△EBC,△CDB,△DEB,其中与△ABC相似的是 △DEB .
27.如图,点P为△ABC的边AB上的一点,添加 ∠APC=∠ACB或∠ACP=∠B或= ,可以使△ABC与△APC相似.
28.如图,在△ABC中,AB=8cm,AC=16cm,点P从A出发,以2cm/s的速度向B运动,同时点Q从C出发,以3cm/s的速度向A运动,当其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为t.
(1)用含t的代数式表示:AQ= (16﹣3t)cm ;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间t= 4或 .
29.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=3,BC=4,DF=6,DE=8,判定这两个三角形是否相似. 不相似 .(填“相似”或“不相似”)
30.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当△APB和△CPD相似时,PD= 12或2或 cm.
31.如图,在正方形ABCD的外侧,以AD为边作等边三角形AED,连接AC交BE于点F,则= 2﹣ .
32.如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F,G,BC=3,AF:FG:GD=3:2:1,则AB的长为 .
33.如图,在△ABC中,AD为∠CAB的平分线,DE∥AB,若DE=3,CE=4,则AB的值 .
34.中国教育家孔子周游列国14年,其中10年居卫(卫国即现在的濮阳),龙湖论语广场有一尊孔子雕像,数学兴趣小组的同学为了测量雕像的高度AB(顶端A到水平地面BE的距离),在雕像旁边的水平地面上C处放了一面镜子(平面镜的厚度忽略不计),组长小丽沿直线BC后退到点E处,这时恰好在镜子里看到雕像的顶端A,此时测得BC=7米,EC=2米,小丽的眼睛距地面的高度DE=1.6米,则雕像的高度AB= 5.6 米.
35.如图是步枪在瞄准时的示意图,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,若从眼睛到准星的距离OE为0.5m,则眼睛到目标的距离OF为 125 m.
三.解答题
36.
解:∵∠ABC=∠EDC=90°,∠ACB=∠ACD,
∴△ABC∽△EDC,
∴,即,
解得:DE=2000,
2000cm=20m,
答:旗杆DE的高度为20m.
37.
(1)证明:∵四边形ABCD为平行四边形,
∴DC∥AB,AD∥BC,
∴△CEG∽△AED,△DEC∽△FEA,
∴,
∴;
(2)解:∵,
∴,
解得DE=8.
38.
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DBC=∠BDA,
∵∠BDA=∠BAE,
∴∠DBC=∠BAE,
∵∠BEF=∠BEA,
∴△EBF∽△EAB,
∴,
∴BE2=EF AE;
(2)解:∵BE2=EF AE,且BE=4,EF=2,
∴AE===8,
∴AF=AE﹣EF=8﹣2=6,
∵BE∥AD,
∴=,
即=,解得BF=2,
∵△EBF∽△EAB,
∴=,
即=,
∴AB=4.
39.
证明:∵BE=BC,
∴∠C=∠CEB,
∵∠CEB=∠AED,
∴∠C=∠AED,
∵AD⊥BE,
∴∠D=∠ABC=90°,
∴△ADE∽△ABC.
40.
证明:∵BF=3,CF=5,
∴BC=BF+CF=8,
∵DE=15,DF=25.∠E=90°,
∴EF==20,
∴,,
∴,
∵∠B=∠E=90°,
∴△ABC∽△DEF.
一.选择题
1.两个三角形相似比是2:3,其中小三角形的周长为18,则另一个大三角形的周长是( )
A.12 B.18 C.24 D.27
2.已知两个相似三角形的周长比为2:3,若较大三角形的面积等于18cm2,则较小三角形的面积等于( )
A.8cm2 B.12cm2 C.27cm2 D.40.5cm2
3.已知△ABC∽△DEF,=,若BC=2,则EF=( )
A.4 B.6 C.8 D.16
4.在一张复印出来的纸上,一个三角形的一条边由原图中的2cm增加了4cm,则复印出的三角形的面积是原图中三角形面积的( )
A.4倍 B.6倍 C.9倍 D.12倍
5.如图,在△ABC中,DE∥BC,DE=2,BC=5,则S△ADE:S△ABC的值是( )
A. B. C. D.
6.如图,点D在△ABC的边AC上,添加一个条件,使得△ADB∽△ABC,下列不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
7.如图,D,E是△ABC边上的两个点,请你再添加一个条件,使得△ABC∽△AED,则下列选项不成立的是( )
A.= B.= C.∠C=∠ADE D.∠B=∠AED
8.如图,△ABC,AB=12,AC=15,D为AB上一点,且AD=8,在AC上取一点E,使以A、D、E为顶点的三角形与ABC相似,则AE等于( )
A.或 B.10或
C.或10 D.以上答案都不对
9.如图,在正方形网格中有5个格点三角形,分别是:①△ABC,②△ACD,③△ADE,④△AEF,⑤△AGH,其中与⑤相似的三角形是( )
A.①③ B.①④ C.②④ D.①③④
10.如图,在菱形ABCD中,点E在AD边上,EF∥CD,交对角线BD于点F,则下列结论中错误的是( )
A.= B. C.= D.=
11.如图,△ABC中,D是AB边上一点,DE∥BC交AC于点E,连接BE,DF∥BE交AC于点F,则下列结论正确的是( )
A. B. C. D.
12.如图, ABCD中,E是AB延长线上一点,DE交BC于点F,且BE:AB=3:2,AD=10,则CF=( )
A.2 B.3 C.4 D.6
13.在《寺庙难题》书中,有这样一道题:五个正方形ABCD,CEFG,FHMN,GNPQ,DGST如图所示排列,其中点A,B、E,H,M共线,可得结论:正方形CEFG与△SGQ的面积相等.若正方形CEFG与△SGQ的面积之和为120,则正方形DGST与正方形GNPQ面积之和为( )
A.270 B.300 C.320 D.350
14.如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,则S△MDN:S△BCD=( )
A.1:3 B.1:5 C.2:3 D.1:6
15.如图中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF.观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论正确的是( )
A. B. C. D.
16.如图,有一块等腰三角形材料,底边BC=80cm,高AD=120cm,现要把它加工成正方形零件,使其一边在BC边上,其余两个顶点分别在AB、AC上,则这个正方形零件的边长为( )
A.36cm B.40cm C.48cm D.60cm
17.如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图,在点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,CD⊥BD,且测得AB=4m,BP=6m,PD=12m,那么该古城墙CD的高度是( )
A.8m B.9m C.16m D.18m
18.如图,有一块三角形余料ABC,BC=120mm,高线AD=90mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P、M分别在AB,AC上,若满足PM:PQ=2:1,则PQ的长为( )
A.36mm B.40mm C.50mm D.120mm
19.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=6,AD=3.6,则BD的长为( )
A.8 B.7.2 C.6.4 D.4.4
二.填空题
20.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 .
21.已知△ABC∽△DEF,相似比为,且△DEF的周长为18,则△ABC的周长为 .
22.如图,已知△ABC∽△ADB,点D是AC的中点,CD=2,则AB的长为 .
23.如图,△ABC∽△CBD,AB=9,BD=25,则BC= .
24.如图,已知△ABC∽△DEF,AB:DE=1:2,点M、N分别是BC、EF的中点,则AM:DN= .
25.如图,Rt△ABC中,∠ACB=90°,在BC的延长线上截取BD=AB,连接AD,过点B作BE⊥AD于点E,交AC于点F,连接DF,点P为射线BE上一个动点,若AC=9,BC=12,当△APB与△AFD相似时,BP的长为 .
26.如图,在正方形网格中有三个三角形,分别是△EBC,△CDB,△DEB,其中与△ABC相似的是 .
27.如图,点P为△ABC的边AB上的一点,添加 ,可以使△ABC与△APC相似.
28.如图,在△ABC中,AB=8cm,AC=16cm,点P从A出发,以2cm/s的速度向B运动,同时点Q从C出发,以3cm/s的速度向A运动,当其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为t.
(1)用含t的代数式表示:AQ= ;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间t= .
29.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=3,BC=4,DF=6,DE=8,判定这两个三角形是否相似. .(填“相似”或“不相似”)
30.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当△APB和△CPD相似时,PD= cm.
31.如图,在正方形ABCD的外侧,以AD为边作等边三角形AED,连接AC交BE于点F,则= .
32.如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F,G,BC=3,AF:FG:GD=3:2:1,则AB的长为 .
33.如图,在△ABC中,AD为∠CAB的平分线,DE∥AB,若DE=3,CE=4,则AB的值 .
34.中国教育家孔子周游列国14年,其中10年居卫(卫国即现在的濮阳),龙湖论语广场有一尊孔子雕像,数学兴趣小组的同学为了测量雕像的高度AB(顶端A到水平地面BE的距离),在雕像旁边的水平地面上C处放了一面镜子(平面镜的厚度忽略不计),组长小丽沿直线BC后退到点E处,这时恰好在镜子里看到雕像的顶端A,此时测得BC=7米,EC=2米,小丽的眼睛距地面的高度DE=1.6米,则雕像的高度AB= 米.
35.如图是步枪在瞄准时的示意图,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,若从眼睛到准星的距离OE为0.5m,则眼睛到目标的距离OF为 m.
三.解答题
36.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是40cm,镜面中心C距离旗杆底部D的距离为5m,如图所示,已知小丽同学的身高是1.66m,眼睛位置A距离小丽头顶的距离是6cm,求出旗杆DE的高度.
37.如图F为平行四边形ABCD的边AB延长线上一点,DF分别交CB、AC于G、E.
(1)求证:;
(2)若EF=16,GE=4,求DE.
38.如图,四边形ABCD为平行四边形,E为边BC上一点,连接BD、AE,它们相交于点F,且∠BDA=∠BAE.
(1)求证:BE2=EF AE;
(2)若BE=4,EF=2,DF=6,求AB的长.
39.如图,在Rt△ABC中,∠ABC=90°,E是边AC上一点,且BE=BC,过点A作BE的垂线,交BE的延长线于点D,求证:△ADE∽△ABC.
40.如图,已知∠B=∠E=90°,AB=6,BF=3,CF=5,DE=15,DF=25.
求证:△ABC∽△DEF.
23.3相似三角形课堂练习---吉林省榆树市八号镇第一中学2022-2023学年华东师大版九年级数学上册
参考答案
一.选择题
1. D.2. A.3. A.4. C.5. B.6. C.7. B.8. C.9. A.10. C.11. A.12. C.13. B.14. D.15. D.16. C.17. A.18. A.19. C.
二.填空题
20.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,BD=3,CD=12,则AD的长为 6 .
21.已知△ABC∽△DEF,相似比为,且△DEF的周长为18,则△ABC的周长为 12 .
22.如图,已知△ABC∽△ADB,点D是AC的中点,CD=2,则AB的长为 2 .
23.如图,△ABC∽△CBD,AB=9,BD=25,则BC= 15 .
24.如图,已知△ABC∽△DEF,AB:DE=1:2,点M、N分别是BC、EF的中点,则AM:DN= 1:2 .
25.如图,Rt△ABC中,∠ACB=90°,在BC的延长线上截取BD=AB,连接AD,过点B作BE⊥AD于点E,交AC于点F,连接DF,点P为射线BE上一个动点,若AC=9,BC=12,当△APB与△AFD相似时,BP的长为 或9 .
26.如图,在正方形网格中有三个三角形,分别是△EBC,△CDB,△DEB,其中与△ABC相似的是 △DEB .
27.如图,点P为△ABC的边AB上的一点,添加 ∠APC=∠ACB或∠ACP=∠B或= ,可以使△ABC与△APC相似.
28.如图,在△ABC中,AB=8cm,AC=16cm,点P从A出发,以2cm/s的速度向B运动,同时点Q从C出发,以3cm/s的速度向A运动,当其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为t.
(1)用含t的代数式表示:AQ= (16﹣3t)cm ;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间t= 4或 .
29.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=3,BC=4,DF=6,DE=8,判定这两个三角形是否相似. 不相似 .(填“相似”或“不相似”)
30.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当△APB和△CPD相似时,PD= 12或2或 cm.
31.如图,在正方形ABCD的外侧,以AD为边作等边三角形AED,连接AC交BE于点F,则= 2﹣ .
32.如图,将一张直角三角形纸片BEC的斜边放在矩形ABCD的BC边上,恰好完全重合,BE、CE分别交AD于点F,G,BC=3,AF:FG:GD=3:2:1,则AB的长为 .
33.如图,在△ABC中,AD为∠CAB的平分线,DE∥AB,若DE=3,CE=4,则AB的值 .
34.中国教育家孔子周游列国14年,其中10年居卫(卫国即现在的濮阳),龙湖论语广场有一尊孔子雕像,数学兴趣小组的同学为了测量雕像的高度AB(顶端A到水平地面BE的距离),在雕像旁边的水平地面上C处放了一面镜子(平面镜的厚度忽略不计),组长小丽沿直线BC后退到点E处,这时恰好在镜子里看到雕像的顶端A,此时测得BC=7米,EC=2米,小丽的眼睛距地面的高度DE=1.6米,则雕像的高度AB= 5.6 米.
35.如图是步枪在瞄准时的示意图,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,若从眼睛到准星的距离OE为0.5m,则眼睛到目标的距离OF为 125 m.
三.解答题
36.
解:∵∠ABC=∠EDC=90°,∠ACB=∠ACD,
∴△ABC∽△EDC,
∴,即,
解得:DE=2000,
2000cm=20m,
答:旗杆DE的高度为20m.
37.
(1)证明:∵四边形ABCD为平行四边形,
∴DC∥AB,AD∥BC,
∴△CEG∽△AED,△DEC∽△FEA,
∴,
∴;
(2)解:∵,
∴,
解得DE=8.
38.
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠DBC=∠BDA,
∵∠BDA=∠BAE,
∴∠DBC=∠BAE,
∵∠BEF=∠BEA,
∴△EBF∽△EAB,
∴,
∴BE2=EF AE;
(2)解:∵BE2=EF AE,且BE=4,EF=2,
∴AE===8,
∴AF=AE﹣EF=8﹣2=6,
∵BE∥AD,
∴=,
即=,解得BF=2,
∵△EBF∽△EAB,
∴=,
即=,
∴AB=4.
39.
证明:∵BE=BC,
∴∠C=∠CEB,
∵∠CEB=∠AED,
∴∠C=∠AED,
∵AD⊥BE,
∴∠D=∠ABC=90°,
∴△ADE∽△ABC.
40.
证明:∵BF=3,CF=5,
∴BC=BF+CF=8,
∵DE=15,DF=25.∠E=90°,
∴EF==20,
∴,,
∴,
∵∠B=∠E=90°,
∴△ABC∽△DEF.
