人教版数学九年级上册 第23章 单元测试(Word版,含解析)
文档属性
| 名称 | 人教版数学九年级上册 第23章 单元测试(Word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 176.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 15:24:48 | ||
图片预览




文档简介
人教九年级上 单元测试
第23章
班级________ 姓名________
一、选择题(每题3分,共30分)
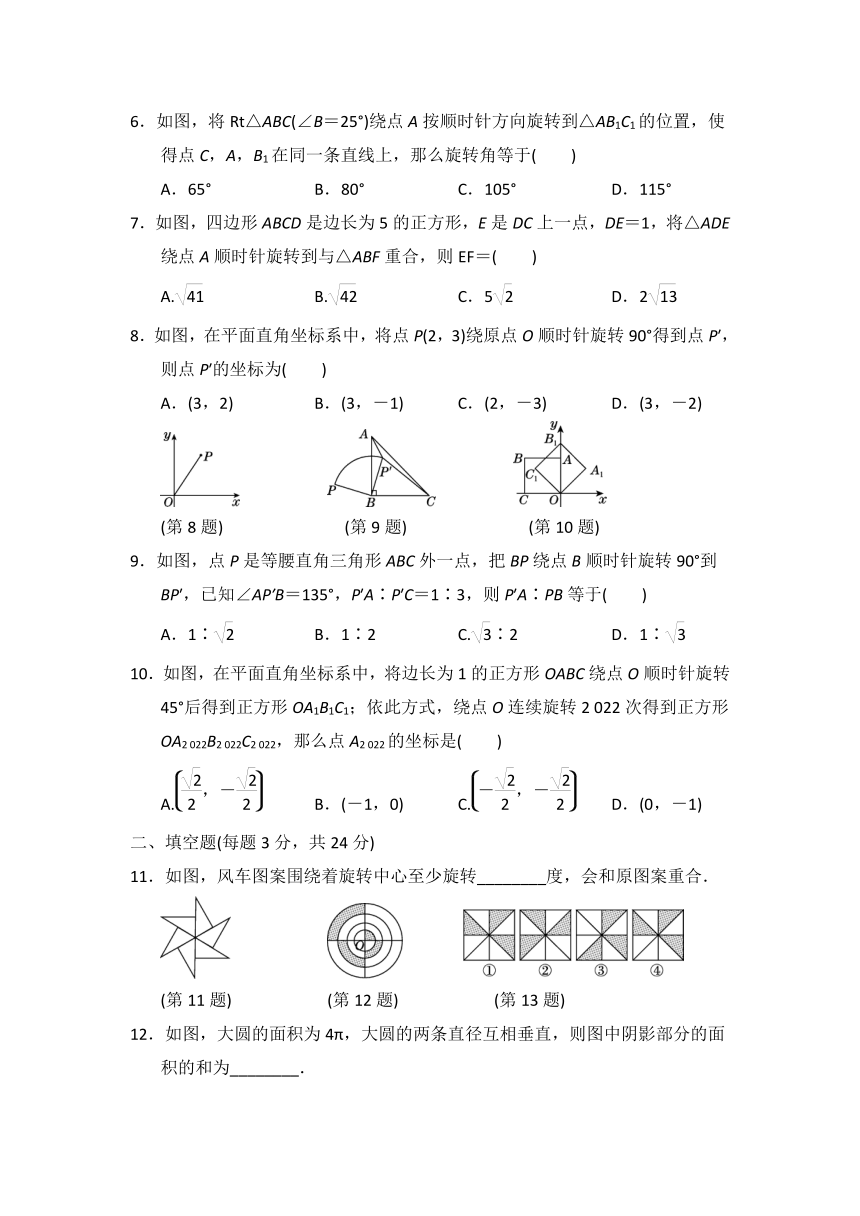
1.垃圾混置是垃圾,垃圾分类是资源.下列可回收物、有害垃圾、厨余垃圾、其他垃圾四种垃圾回收标识中,既是轴对称图形又是中心对称图形的是( )
2.如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )
3.点(-1,2)关于原点的对称点坐标是( )
A.(-1,-2) B.(1,-2) C.(1,2) D.(2,-1)
4.如图,四边形ABCD为正方形,O为对角线AC,BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA?( )
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
(第4题) (第5题) (第6题) (第7题)
5.如图,点O是 ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABOE和四边形CDOF的面积分别记为S1,S2,那么S1,S2之间的关系为( )
A. S1>S2 B. S16.如图,将Rt△ABC(∠B=25°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
A.65° B.80° C.105° D.115°
7.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕点A顺时针旋转到与△ABF重合,则EF=( )
A. B. C.5 D.2
8.如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P′,则点P′的坐标为( )
A.(3,2) B.(3,-1) C.(2,-3) D.(3,-2)
(第8题) (第9题) (第10题)
9.如图,点P是等腰直角三角形ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB等于( )
A.1∶ B.1∶2 C.∶2 D.1∶
10.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1;依此方式,绕点O连续旋转2 022次得到正方形OA2 022B2 022C2 022,那么点A2 022的坐标是( )
A. B.(-1,0) C. D.(0,-1)
二、填空题(每题3分,共24分)
11.如图,风车图案围绕着旋转中心至少旋转________度,会和原图案重合.
(第11题) (第12题) (第13题)
12.如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为________.
13.如图所示,图形①经过________变换得到图形②;图形①经过________变换得到图形③;图形①经过________变换得到图形④.(填“平移”“旋转”或“轴对称”)
14.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=________.
(第14题) (第15题) (第16题) (第17题)
15.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形,若点A的坐标是(1,3),则点M的坐标是__________,点N的坐标是__________.
16.如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O按逆时针方向旋转90°得到△OA1B1.连接AA1,则四边形OAA1B1的面积为________.
17.如图,将△ABC在平面内绕点A逆时针旋转40°到△AB′C′的位置,若CC′∥AB,则∠CAB′的度数为________.
18.如图,将一个45°角的顶点与正方形ABCD的顶点A重合,在正方形的内部绕着点A旋转,角的两边分别与CD,CB边相交于F,E两点,与对角线BD交于N,M两点,连接EF,则下列结论:
①AE=AF;②EF=BE+DF;
③△CEF的周长等于正方形ABCD周长的一半;④S△AEF=S△ABE+S△ADF.
其中正确的结论有____________(填序号).
三、解答题(19~22题每题8分,23题10分,其余每题12分,共66分)
19.如图,在△ABC中,∠B=10°,∠ACB=20°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转角的度数;
(2)求∠BAE的度数和AE的长.
20.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2,C2的坐标.
21.平面直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
22.如图,在6×6的网格中已经涂黑了三个小正方形,请按下列要求画图.
(1)在图①中涂黑一个小正方形,使涂黑的四个小正方形组成一个轴对称图形.
(2)在图②中涂黑一个小正方形,使涂黑的四个小正方形组成一个中心对称图形.
23.如图,△BAD是由△BEC在平面内绕点B旋转60°得到的,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
24.已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
25.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图①,直接写出∠ABD的大小(用含α的式子表示);
(2)如图②,∠BCE=150°,∠ABE=60°,试判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α.
参考答案
一、1.B 2.C 3.B 4.C 5.C 6.D 7.D 8.D 9.B 10.B
二、11.60 12.π 13.轴对称;旋转;平移
14. 15.(-1,-3);(1,-3)
16. 36 17.30°
18.②③④
三、19.解:(1)旋转中心是点A.
∵∠CAB=180°-∠B-∠ACB=150°,∴旋转角是150°.
(2)∠BAE=360°-150°×2=60°.
由旋转的性质得△ABC≌△ADE,
∴AB=AD,AC=AE.
又∵点C是AD的中点,
∴AC=AD=AB=×4=2.∴AE=2.
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△AB2C2即为所求.
点B2的坐标为(4,-2),点C2的坐标为(1,-3).
21.解:根据题意,得(x2+2x)+(x+2)=0,y=-3.
解得x1=-1,x2=-2.
∵点P在第二象限,∴x2+2x<0.
∴x=-1.∴x+2y=-7.
22.解:(1)如图①所示:①、②、③、④处涂黑都可以使涂黑的四个小正方形组成一个轴对称图形;
(2)如图②所示:①、②处涂黑都可以使涂黑的四个小正方形组成一个中心对称图形.
23.(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°得到的,
∴DB=CB,∠ABE=∠DBC=60°.
∵AB⊥BC,∴∠ABC=90°.∴∠CBE=30°.
∴∠DBE=30°.∴∠DBE=∠CBE.
在△BDE和△BCE中,DB=CB,∠DBE=∠CBE,BE=BE,
∴△BDE≌△BCE(SAS).
(2)解:四边形ABED为菱形.
理由:由(1)得△BDE≌△BCE,∴EC=ED.
∵△BAD是由△BEC旋转得到的,∴△BAD≌△BEC.
∴BA=BE,AD=EC.
又∵BE=CE,EC=ED,∴BA=BE=AD=ED.
∴四边形ABED为菱形.
24. 点方法:(1)可以用观察法初步判断AE和DB的数量、位置关系,通过边长DB交AE于点M,利用全等的知识进行验证.
解:(1)AE=DB,AE⊥DB.
理由:如图①,延长DB交AE于点M.由题意可知,CA=CB,CE=CD,∠ACE=∠BCD=90°,
∴△ACE≌△BCD(SAS).
∴AE=DB,∠AEC=∠BDC.
∵∠ACE=90°,∴∠AEC+∠EAC=90°,
∴∠BDC+∠EAC=90°.
∴在△AMD中,∠AMD=180°-90°=90°.
∴AE⊥DB.
(2)DE=AF,DE⊥AF.
理由:如图②,设ED与AF相交于点N,由题意易知BE=AD.
∵∠EBD=∠C+∠BDC=90°+∠BDC,
∠ADF=∠BDF+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF.又∵DB=DF,
∴△EBD≌△ADF(SAS).
∴∠E=∠FAD,DE=AF.
∵∠E=45°,∴∠FAD=45°.
又∵∠EDC=45°,∴∠AND=90°.∴DE⊥AF.
25.解:(1)∠ABD=30°-α.
(2)△ABE 为等边三角形.证明如下:
连接 AD,CD.
∵线段 BC 绕点 B 逆时针旋转 60° 得到线段BD,
∴BC=BD,∠DBC=60°.∴△BCD是等边三角形.∴BD=CD.∵∠ABE= 60°,
∴∠ABD= 60°-∠DBE=∠EBC=30°-α.
在△ABD和△ACD中,
AB=AC,AD=AD,BD=CD,
∴ △ABD≌△ACD(SSS).
∴∠BAD=∠CAD=∠BAC=α.
∵∠BCE=150°,
∴∠BEC=180°--150°=α.
∴∠BAD=∠BEC.
在△ABD和△EBC中,
∠BAD=∠BEC,∠ABD=∠EBC,BD=BC,
∴△ABD≌△EBC(AAS).∴AB=BE.
又∵∠ABE=60°,∴△ABE为等边三角形.
(3)由(2)可知△BCD为等边三角形,∴∠BCD=60°.
∵∠BCE=150°,∴∠DCE=150°-60°=90°.
∵∠DEC=45°,∴ △DCE为等腰直角三角形,
∴DC=CE=BC.∴∠CBE=∠BEC.
∵∠BCE=150°,
∴∠EBC==15°.
而由(2)知∠EBC=30°-α,
∴30°-α=15°.∴α=30°.
10 / 10
第23章
班级________ 姓名________
一、选择题(每题3分,共30分)
1.垃圾混置是垃圾,垃圾分类是资源.下列可回收物、有害垃圾、厨余垃圾、其他垃圾四种垃圾回收标识中,既是轴对称图形又是中心对称图形的是( )
2.如图,将方格纸中的图形绕点O逆时针旋转90°后得到的图形是( )
3.点(-1,2)关于原点的对称点坐标是( )
A.(-1,-2) B.(1,-2) C.(1,2) D.(2,-1)
4.如图,四边形ABCD为正方形,O为对角线AC,BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA?( )
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
(第4题) (第5题) (第6题) (第7题)
5.如图,点O是 ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABOE和四边形CDOF的面积分别记为S1,S2,那么S1,S2之间的关系为( )
A. S1>S2 B. S1
A.65° B.80° C.105° D.115°
7.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕点A顺时针旋转到与△ABF重合,则EF=( )
A. B. C.5 D.2
8.如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P′,则点P′的坐标为( )
A.(3,2) B.(3,-1) C.(2,-3) D.(3,-2)
(第8题) (第9题) (第10题)
9.如图,点P是等腰直角三角形ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB等于( )
A.1∶ B.1∶2 C.∶2 D.1∶
10.如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1;依此方式,绕点O连续旋转2 022次得到正方形OA2 022B2 022C2 022,那么点A2 022的坐标是( )
A. B.(-1,0) C. D.(0,-1)
二、填空题(每题3分,共24分)
11.如图,风车图案围绕着旋转中心至少旋转________度,会和原图案重合.
(第11题) (第12题) (第13题)
12.如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为________.
13.如图所示,图形①经过________变换得到图形②;图形①经过________变换得到图形③;图形①经过________变换得到图形④.(填“平移”“旋转”或“轴对称”)
14.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=________.
(第14题) (第15题) (第16题) (第17题)
15.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形,若点A的坐标是(1,3),则点M的坐标是__________,点N的坐标是__________.
16.如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O按逆时针方向旋转90°得到△OA1B1.连接AA1,则四边形OAA1B1的面积为________.
17.如图,将△ABC在平面内绕点A逆时针旋转40°到△AB′C′的位置,若CC′∥AB,则∠CAB′的度数为________.
18.如图,将一个45°角的顶点与正方形ABCD的顶点A重合,在正方形的内部绕着点A旋转,角的两边分别与CD,CB边相交于F,E两点,与对角线BD交于N,M两点,连接EF,则下列结论:
①AE=AF;②EF=BE+DF;
③△CEF的周长等于正方形ABCD周长的一半;④S△AEF=S△ABE+S△ADF.
其中正确的结论有____________(填序号).
三、解答题(19~22题每题8分,23题10分,其余每题12分,共66分)
19.如图,在△ABC中,∠B=10°,∠ACB=20°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转角的度数;
(2)求∠BAE的度数和AE的长.
20.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2,C2的坐标.
21.平面直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
22.如图,在6×6的网格中已经涂黑了三个小正方形,请按下列要求画图.
(1)在图①中涂黑一个小正方形,使涂黑的四个小正方形组成一个轴对称图形.
(2)在图②中涂黑一个小正方形,使涂黑的四个小正方形组成一个中心对称图形.
23.如图,△BAD是由△BEC在平面内绕点B旋转60°得到的,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
24.已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
25.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图①,直接写出∠ABD的大小(用含α的式子表示);
(2)如图②,∠BCE=150°,∠ABE=60°,试判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α.
参考答案
一、1.B 2.C 3.B 4.C 5.C 6.D 7.D 8.D 9.B 10.B
二、11.60 12.π 13.轴对称;旋转;平移
14. 15.(-1,-3);(1,-3)
16. 36 17.30°
18.②③④
三、19.解:(1)旋转中心是点A.
∵∠CAB=180°-∠B-∠ACB=150°,∴旋转角是150°.
(2)∠BAE=360°-150°×2=60°.
由旋转的性质得△ABC≌△ADE,
∴AB=AD,AC=AE.
又∵点C是AD的中点,
∴AC=AD=AB=×4=2.∴AE=2.
20.解:(1)如图,△A1B1C1即为所求.
(2)如图,△AB2C2即为所求.
点B2的坐标为(4,-2),点C2的坐标为(1,-3).
21.解:根据题意,得(x2+2x)+(x+2)=0,y=-3.
解得x1=-1,x2=-2.
∵点P在第二象限,∴x2+2x<0.
∴x=-1.∴x+2y=-7.
22.解:(1)如图①所示:①、②、③、④处涂黑都可以使涂黑的四个小正方形组成一个轴对称图形;
(2)如图②所示:①、②处涂黑都可以使涂黑的四个小正方形组成一个中心对称图形.
23.(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°得到的,
∴DB=CB,∠ABE=∠DBC=60°.
∵AB⊥BC,∴∠ABC=90°.∴∠CBE=30°.
∴∠DBE=30°.∴∠DBE=∠CBE.
在△BDE和△BCE中,DB=CB,∠DBE=∠CBE,BE=BE,
∴△BDE≌△BCE(SAS).
(2)解:四边形ABED为菱形.
理由:由(1)得△BDE≌△BCE,∴EC=ED.
∵△BAD是由△BEC旋转得到的,∴△BAD≌△BEC.
∴BA=BE,AD=EC.
又∵BE=CE,EC=ED,∴BA=BE=AD=ED.
∴四边形ABED为菱形.
24. 点方法:(1)可以用观察法初步判断AE和DB的数量、位置关系,通过边长DB交AE于点M,利用全等的知识进行验证.
解:(1)AE=DB,AE⊥DB.
理由:如图①,延长DB交AE于点M.由题意可知,CA=CB,CE=CD,∠ACE=∠BCD=90°,
∴△ACE≌△BCD(SAS).
∴AE=DB,∠AEC=∠BDC.
∵∠ACE=90°,∴∠AEC+∠EAC=90°,
∴∠BDC+∠EAC=90°.
∴在△AMD中,∠AMD=180°-90°=90°.
∴AE⊥DB.
(2)DE=AF,DE⊥AF.
理由:如图②,设ED与AF相交于点N,由题意易知BE=AD.
∵∠EBD=∠C+∠BDC=90°+∠BDC,
∠ADF=∠BDF+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF.又∵DB=DF,
∴△EBD≌△ADF(SAS).
∴∠E=∠FAD,DE=AF.
∵∠E=45°,∴∠FAD=45°.
又∵∠EDC=45°,∴∠AND=90°.∴DE⊥AF.
25.解:(1)∠ABD=30°-α.
(2)△ABE 为等边三角形.证明如下:
连接 AD,CD.
∵线段 BC 绕点 B 逆时针旋转 60° 得到线段BD,
∴BC=BD,∠DBC=60°.∴△BCD是等边三角形.∴BD=CD.∵∠ABE= 60°,
∴∠ABD= 60°-∠DBE=∠EBC=30°-α.
在△ABD和△ACD中,
AB=AC,AD=AD,BD=CD,
∴ △ABD≌△ACD(SSS).
∴∠BAD=∠CAD=∠BAC=α.
∵∠BCE=150°,
∴∠BEC=180°--150°=α.
∴∠BAD=∠BEC.
在△ABD和△EBC中,
∠BAD=∠BEC,∠ABD=∠EBC,BD=BC,
∴△ABD≌△EBC(AAS).∴AB=BE.
又∵∠ABE=60°,∴△ABE为等边三角形.
(3)由(2)可知△BCD为等边三角形,∴∠BCD=60°.
∵∠BCE=150°,∴∠DCE=150°-60°=90°.
∵∠DEC=45°,∴ △DCE为等腰直角三角形,
∴DC=CE=BC.∴∠CBE=∠BEC.
∵∠BCE=150°,
∴∠EBC==15°.
而由(2)知∠EBC=30°-α,
∴30°-α=15°.∴α=30°.
10 / 10
同课章节目录
