苏科版数学八年级上册 2.1轴对称与轴对称图形 随堂测试(Word版,含答案)
文档属性
| 名称 | 苏科版数学八年级上册 2.1轴对称与轴对称图形 随堂测试(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 612.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览

文档简介
随堂测试
2.1轴对称与轴对称图形
一.选择题(每小题2分 共40分)
1.下列说法不正确的是( )
A.对称轴是一条直线
B.两个关于某直线对称的三角形一定全等
C.若△ABC与△A′B′C′关于直线l对称,则其对应边上的高中线、对应角平分线也分别关于直线l对称
D.两个全等的三角形一定关于某条直线对称
2.下列图形中,有无数条对称轴的是( )
A.长方形 B.正方形 C.圆 D.等腰三角形
3.下列图形中,点P与点G关于直线对称的是( )
A B C D
4.如图1.2-1,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
A、5cm B、10cm C、20cm D、15cm
5.如图是把一张长方形的纸沿长边中点的连线对折两次后得到的图形.再沿虚线裁剪,外面部分展开后的图形是( )
A.B.C. D.
6.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.30° B.45° C.60° D.75°
7.一张正方形纸片经过两次对折,并在如图1位置上剪去一个小正方形,打开后是( )
8.如图,是一个经改造的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,若一个球按图中所示方向被击,该球最后落入1号袋,经过反射的次数是( )
A. 4次 B. 5次 C. 6次 D. 7次
9.. 下列说法错误的是( )
A. 关于某条直线对称的两个三角形一定全等 B. 轴对称图形至少有一条对称轴
C. 全等三角形一定能关于某条直线对称 D. 角是关于它的平分线对称的图形
10. 下列图形中是轴对称图形的是( )
A B C D
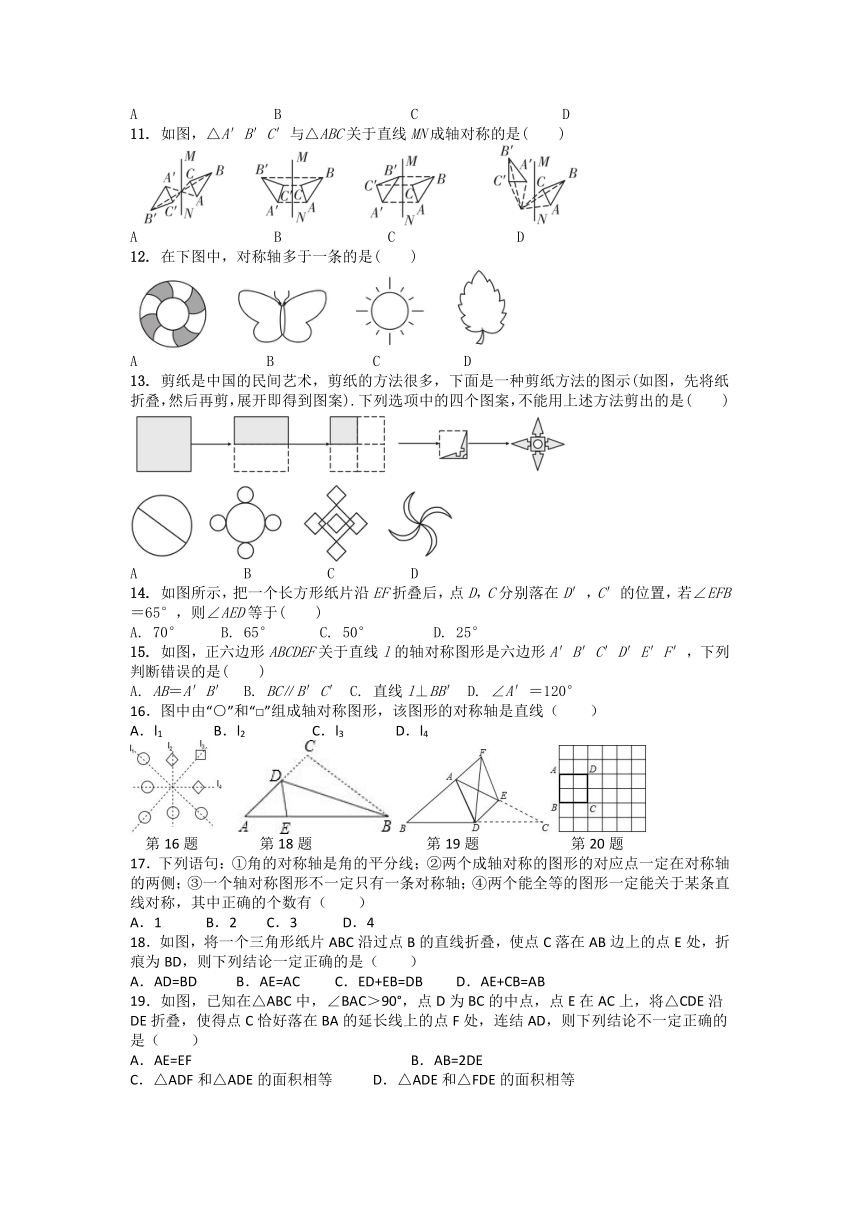
11. 如图,△A′B′C′与△ABC关于直线MN成轴对称的是( )
A B C D
12. 在下图中,对称轴多于一条的是( )
A B C D
13. 剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图,先将纸折叠,然后再剪,展开即得到图案).下列选项中的四个图案,不能用上述方法剪出的是( )
A B C D
14. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED等于( )
A. 70° B. 65° C. 50° D. 25°
15. 如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
A. AB=A′B′ B. BC∥B′C′ C. 直线l⊥BB′ D. ∠A′=120°
16.图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
A.l1 B.l2 C.l3 D.l4
第16题 第18题 第19题 第20题
17.下列语句:①角的对称轴是角的平分线;②两个成轴对称的图形的对应点一定在对称轴的两侧;③一个轴对称图形不一定只有一条对称轴;④两个能全等的图形一定能关于某条直线对称,其中正确的个数有( )
A.1 B.2 C.3 D.4
18.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.AE=AC C.ED+EB=DB D.AE+CB=AB
19.如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A.AE=EF B.AB=2DE
C.△ADF和△ADE的面积相等 D.△ADE和△FDE的面积相等
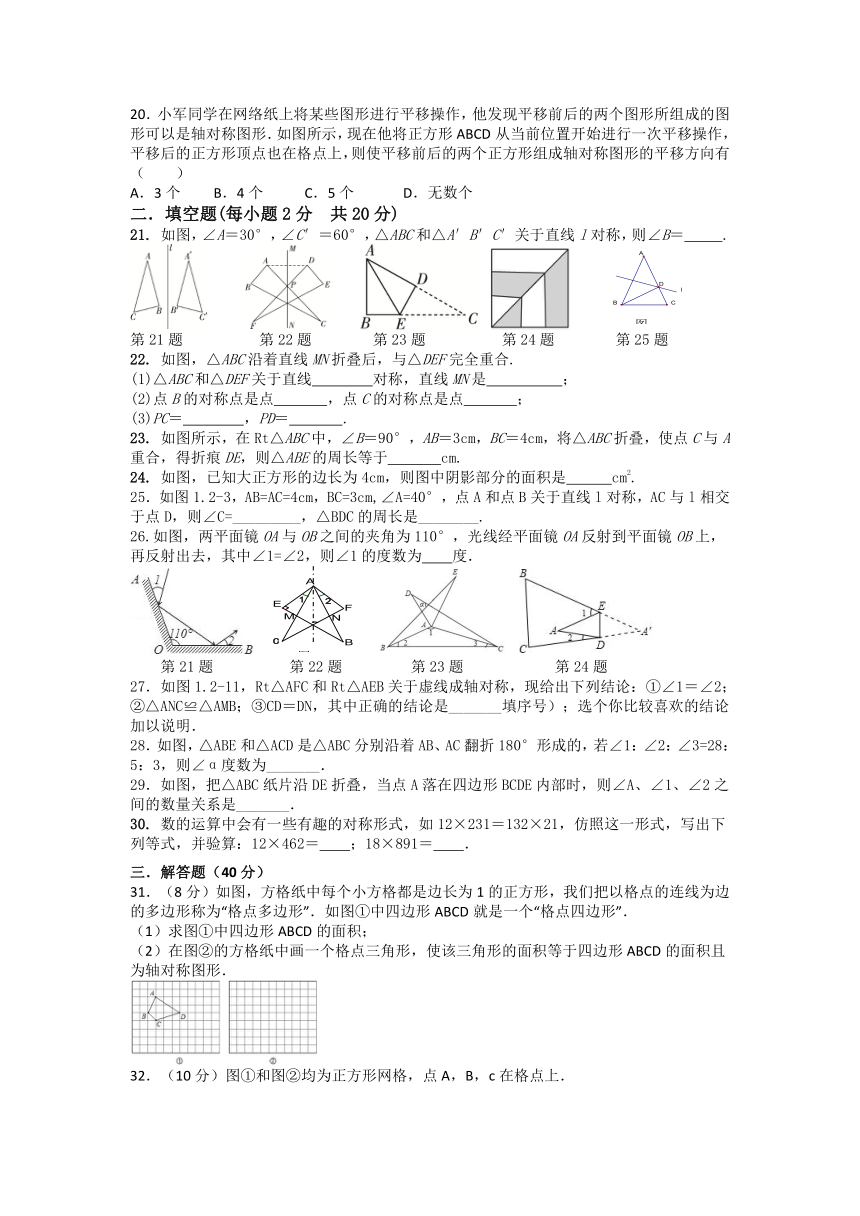
20.小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( )
A.3个 B.4个 C.5个 D.无数个
二.填空题(每小题2分 共20分)
21. 如图,∠A=30°,∠C′=60°,△ABC和△A′B′C′关于直线l对称,则∠B= .
第21题 第22题 第23题 第24题 第25题
22. 如图,△ABC沿着直线MN折叠后,与△DEF完全重合.
(1)△ABC和△DEF关于直线 对称,直线MN是 ;
(2)点B的对称点是点 ,点C的对称点是点 ;
(3)PC= ,PD= .
23. 如图所示,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于 cm.
24. 如图,已知大正方形的边长为4cm,则图中阴影部分的面积是 cm2.
25.如图1.2-3,AB=AC=4cm,BC=3cm,∠A=40°,点A和点B关于直线l对称,AC与l相交于点D,则∠C=_________,△BDC的周长是________.
26.如图,两平面镜OA与OB之间的夹角为110°,光线经平面镜OA反射到平面镜OB上,再反射出去,其中∠1=∠2,则∠1的度数为 度.
第21题 第22题 第23题 第24题
27.如图1.2-11,Rt△AFC和Rt△AEB关于虚线成轴对称,现给出下列结论:①∠1=∠2;②△ANC≌△AMB;③CD=DN,其中正确的结论是_______填序号);选个你比较喜欢的结论加以说明.
28.如图,△ABE和△ACD是△ABC分别沿着AB、AC翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α度数为_______.
29.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A、∠1、∠2之间的数量关系是_______.
30. 数的运算中会有一些有趣的对称形式,如12×231=132×21,仿照这一形式,写出下列等式,并验算:12×462= ;18×891= .
三.解答题(40分)
31.(8分)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点的连线为边的多边形称为“格点多边形”.如图①中四边形ABCD就是一个“格点四边形”.
(1)求图①中四边形ABCD的面积;
(2)在图②的方格纸中画一个格点三角形,使该三角形的面积等于四边形ABCD的面积且为轴对称图形.
32.(10分)图①和图②均为正方形网格,点A,B,c在格点上.
(1)请你分别在图①,图②中确定格点D,画出一个以A,B,C,D为顶点的四边形,使其成为轴对称图形,并画出对称轴,对称轴用直线m表示;
(2)每个小正方形的边长为1,请分别求出图①,图②中以A,B,C,D为顶点的四边形的面积.
33. (10分)如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
34.(12分)(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
①若∠A=58°,求∠DPE的度数;
②请直接写出∠A与∠DPE的数量关系;
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、
P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
参考答案
一.选择题(每小题2分 共40分)
1.D
2.C
3.D
4.B
5.D
6.C
7.B
8.C.
9.C.
10. D.
11. B
12. C
13. D
14. C
15.B
16.C
17.A.
18.D.
19.C
20.C
二.填空题(每小题2分 共20分)
21. 90°
22. (1)MN 对称轴 (2)E F (3)PF PA
23. 7
24. 8
25.70° 7cm
26.35°
27.①②
28.80°
29.∠1+∠2=2∠A
30. 264×21 198×81
三.解答题(40分)
31.
解:(1)四边形ABCD的面积为:×3×4=6 (2)如图所示:
32.
解:(1)如图①、图②所示,四边形ABCD和四边形ABDC即为所求;
(2)如图①,四边形ABCD的面积为:2×4=8;
如图②,四边形ABDC的面积为:×2×(2+4)=6.
33.
解:(1)证明:由题意知∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,∴∠GCF=∠BCE.又∵∠G=∠D=∠B=90°,GC=AD=BC,∴△FGC≌△EBC.
(2)由(1)知,DF=GF=BE,∴四边形ECGF的面积=四边形AEFD的面积===16
34.
解:(1)①∵P1,P2是点P关于AB、AC的对称点,∴PD=P1D,PE=P2E,∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,∵∠DDP1+∠DPE+∠EPP2+∠A=180° ①,
2∠DPP1+∠DPE+2∠EPP2=180° ② ②﹣①得:∠DPP1+∠EPP2=∠A,
∵∠A=58°,∴∠DPP1+∠EPP2=58°∴∠DPE=64°
(2)由(1)可知:∠DPE=180°﹣2∠A.点可知P1,P2与点A在同一条直线上.理由如下:连接AP,AP1,AP2.根据轴对称的性质,可得∠4=∠1,∠3=∠2,
∵∠BAC=90°即∠1+∠2=90°,∴∠3+∠4=90°∴∠1+∠2+∠3+∠4=180°,即∠P1AP2=180°∴点P1,P2与点A在同一条直线上.
第4题
图1.2-3
D
图1.2-11
2.1轴对称与轴对称图形
一.选择题(每小题2分 共40分)
1.下列说法不正确的是( )
A.对称轴是一条直线
B.两个关于某直线对称的三角形一定全等
C.若△ABC与△A′B′C′关于直线l对称,则其对应边上的高中线、对应角平分线也分别关于直线l对称
D.两个全等的三角形一定关于某条直线对称
2.下列图形中,有无数条对称轴的是( )
A.长方形 B.正方形 C.圆 D.等腰三角形
3.下列图形中,点P与点G关于直线对称的是( )
A B C D
4.如图1.2-1,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
A、5cm B、10cm C、20cm D、15cm
5.如图是把一张长方形的纸沿长边中点的连线对折两次后得到的图形.再沿虚线裁剪,外面部分展开后的图形是( )
A.B.C. D.
6.如图,∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1的度数为( )
A.30° B.45° C.60° D.75°
7.一张正方形纸片经过两次对折,并在如图1位置上剪去一个小正方形,打开后是( )
8.如图,是一个经改造的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,若一个球按图中所示方向被击,该球最后落入1号袋,经过反射的次数是( )
A. 4次 B. 5次 C. 6次 D. 7次
9.. 下列说法错误的是( )
A. 关于某条直线对称的两个三角形一定全等 B. 轴对称图形至少有一条对称轴
C. 全等三角形一定能关于某条直线对称 D. 角是关于它的平分线对称的图形
10. 下列图形中是轴对称图形的是( )
A B C D
11. 如图,△A′B′C′与△ABC关于直线MN成轴对称的是( )
A B C D
12. 在下图中,对称轴多于一条的是( )
A B C D
13. 剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸方法的图示(如图,先将纸折叠,然后再剪,展开即得到图案).下列选项中的四个图案,不能用上述方法剪出的是( )
A B C D
14. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED等于( )
A. 70° B. 65° C. 50° D. 25°
15. 如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′,下列判断错误的是( )
A. AB=A′B′ B. BC∥B′C′ C. 直线l⊥BB′ D. ∠A′=120°
16.图中由“○”和“□”组成轴对称图形,该图形的对称轴是直线( )
A.l1 B.l2 C.l3 D.l4
第16题 第18题 第19题 第20题
17.下列语句:①角的对称轴是角的平分线;②两个成轴对称的图形的对应点一定在对称轴的两侧;③一个轴对称图形不一定只有一条对称轴;④两个能全等的图形一定能关于某条直线对称,其中正确的个数有( )
A.1 B.2 C.3 D.4
18.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.AE=AC C.ED+EB=DB D.AE+CB=AB
19.如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A.AE=EF B.AB=2DE
C.△ADF和△ADE的面积相等 D.△ADE和△FDE的面积相等
20.小军同学在网络纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( )
A.3个 B.4个 C.5个 D.无数个
二.填空题(每小题2分 共20分)
21. 如图,∠A=30°,∠C′=60°,△ABC和△A′B′C′关于直线l对称,则∠B= .
第21题 第22题 第23题 第24题 第25题
22. 如图,△ABC沿着直线MN折叠后,与△DEF完全重合.
(1)△ABC和△DEF关于直线 对称,直线MN是 ;
(2)点B的对称点是点 ,点C的对称点是点 ;
(3)PC= ,PD= .
23. 如图所示,在Rt△ABC中,∠B=90°,AB=3cm,BC=4cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于 cm.
24. 如图,已知大正方形的边长为4cm,则图中阴影部分的面积是 cm2.
25.如图1.2-3,AB=AC=4cm,BC=3cm,∠A=40°,点A和点B关于直线l对称,AC与l相交于点D,则∠C=_________,△BDC的周长是________.
26.如图,两平面镜OA与OB之间的夹角为110°,光线经平面镜OA反射到平面镜OB上,再反射出去,其中∠1=∠2,则∠1的度数为 度.
第21题 第22题 第23题 第24题
27.如图1.2-11,Rt△AFC和Rt△AEB关于虚线成轴对称,现给出下列结论:①∠1=∠2;②△ANC≌△AMB;③CD=DN,其中正确的结论是_______填序号);选个你比较喜欢的结论加以说明.
28.如图,△ABE和△ACD是△ABC分别沿着AB、AC翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α度数为_______.
29.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A、∠1、∠2之间的数量关系是_______.
30. 数的运算中会有一些有趣的对称形式,如12×231=132×21,仿照这一形式,写出下列等式,并验算:12×462= ;18×891= .
三.解答题(40分)
31.(8分)如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点的连线为边的多边形称为“格点多边形”.如图①中四边形ABCD就是一个“格点四边形”.
(1)求图①中四边形ABCD的面积;
(2)在图②的方格纸中画一个格点三角形,使该三角形的面积等于四边形ABCD的面积且为轴对称图形.
32.(10分)图①和图②均为正方形网格,点A,B,c在格点上.
(1)请你分别在图①,图②中确定格点D,画出一个以A,B,C,D为顶点的四边形,使其成为轴对称图形,并画出对称轴,对称轴用直线m表示;
(2)每个小正方形的边长为1,请分别求出图①,图②中以A,B,C,D为顶点的四边形的面积.
33. (10分)如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
34.(12分)(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
①若∠A=58°,求∠DPE的度数;
②请直接写出∠A与∠DPE的数量关系;
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、
P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
参考答案
一.选择题(每小题2分 共40分)
1.D
2.C
3.D
4.B
5.D
6.C
7.B
8.C.
9.C.
10. D.
11. B
12. C
13. D
14. C
15.B
16.C
17.A.
18.D.
19.C
20.C
二.填空题(每小题2分 共20分)
21. 90°
22. (1)MN 对称轴 (2)E F (3)PF PA
23. 7
24. 8
25.70° 7cm
26.35°
27.①②
28.80°
29.∠1+∠2=2∠A
30. 264×21 198×81
三.解答题(40分)
31.
解:(1)四边形ABCD的面积为:×3×4=6 (2)如图所示:
32.
解:(1)如图①、图②所示,四边形ABCD和四边形ABDC即为所求;
(2)如图①,四边形ABCD的面积为:2×4=8;
如图②,四边形ABDC的面积为:×2×(2+4)=6.
33.
解:(1)证明:由题意知∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,∴∠GCF=∠BCE.又∵∠G=∠D=∠B=90°,GC=AD=BC,∴△FGC≌△EBC.
(2)由(1)知,DF=GF=BE,∴四边形ECGF的面积=四边形AEFD的面积===16
34.
解:(1)①∵P1,P2是点P关于AB、AC的对称点,∴PD=P1D,PE=P2E,∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,∵∠DDP1+∠DPE+∠EPP2+∠A=180° ①,
2∠DPP1+∠DPE+2∠EPP2=180° ② ②﹣①得:∠DPP1+∠EPP2=∠A,
∵∠A=58°,∴∠DPP1+∠EPP2=58°∴∠DPE=64°
(2)由(1)可知:∠DPE=180°﹣2∠A.点可知P1,P2与点A在同一条直线上.理由如下:连接AP,AP1,AP2.根据轴对称的性质,可得∠4=∠1,∠3=∠2,
∵∠BAC=90°即∠1+∠2=90°,∴∠3+∠4=90°∴∠1+∠2+∠3+∠4=180°,即∠P1AP2=180°∴点P1,P2与点A在同一条直线上.
第4题
图1.2-3
D
图1.2-11
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
