2021--2022学年沪科版数学八年级下册19.1 多边形外角和 课件(共22张PPT)
文档属性
| 名称 | 2021--2022学年沪科版数学八年级下册19.1 多边形外角和 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 11:11:55 | ||
图片预览



文档简介
(共22张PPT)
《§19.1.2多边形外角和》
学习目标
1、经历多边形外角和的探究过程。
2、了解正多边形的定义并会用它解决问题。
3、了解四边形的不稳定性及在实际生活中的应用。
2
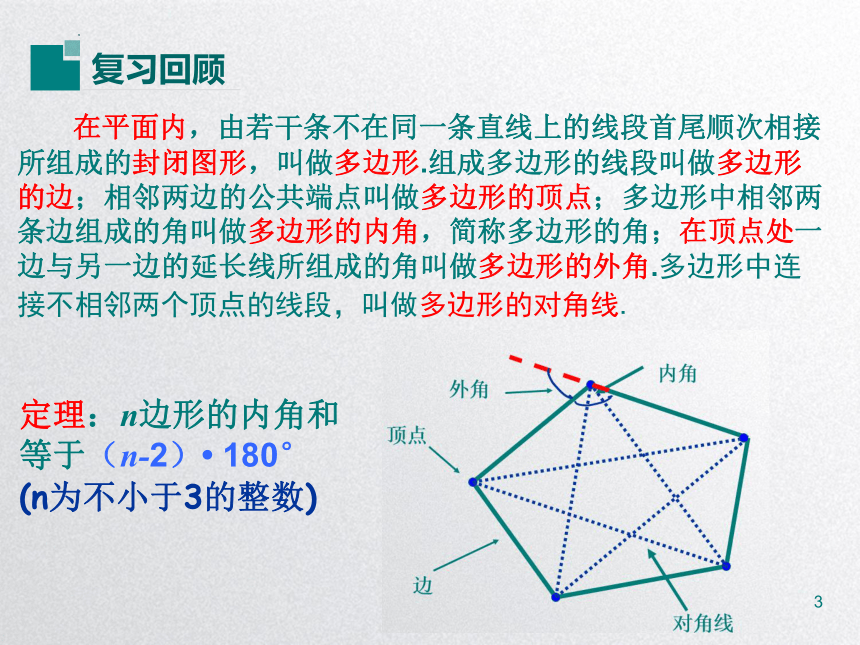
在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的封闭图形,叫做多边形.组成多边形的线段叫做多边形的边;相邻两边的公共端点叫做多边形的顶点;多边形中相邻两条边组成的角叫做多边形的内角,简称多边形的角;在顶点处一边与另一边的延长线所组成的角叫做多边形的外角.多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
定理:n边形的内角和
等于(n-2) 180°
(n为不小于3的整数)
3
复习回顾
三角形
六边形
四边形
八边形
……
五边形
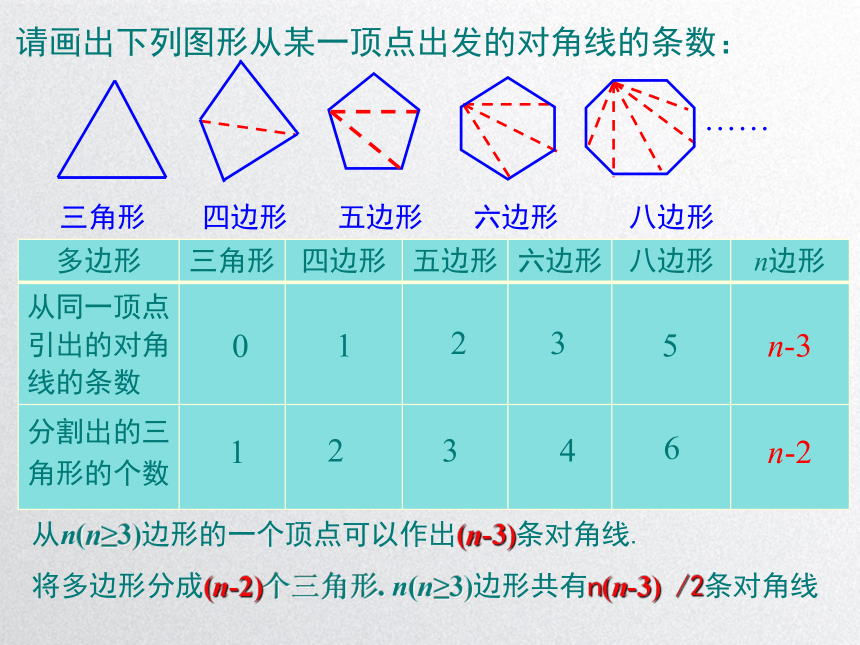
请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形. n(n≥3)边形共有n(n-3) /2条对角线
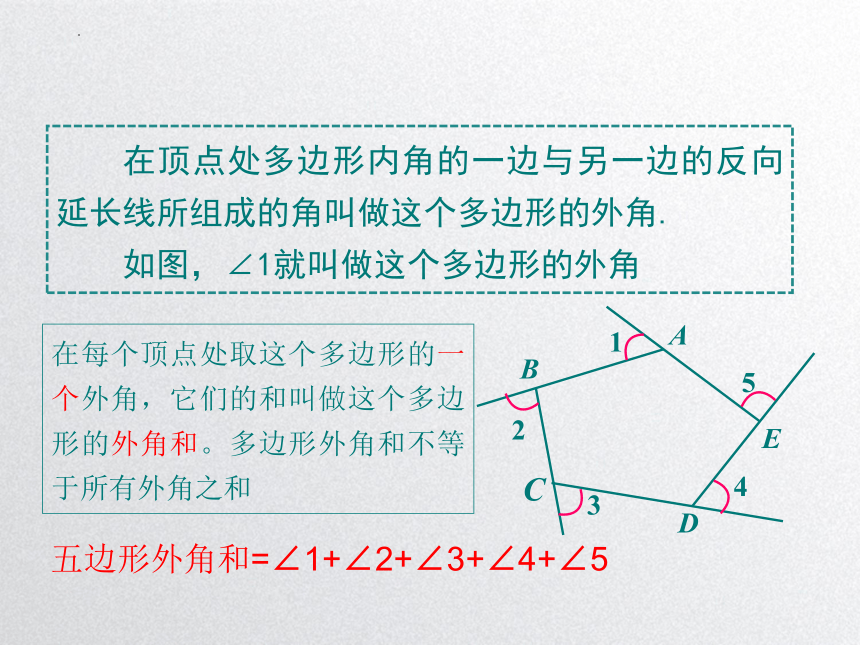
在顶点处多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
如图,∠1就叫做这个多边形的外角
E
B
C
D
1
2
3
4
5
A
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。多边形外角和不等于所有外角之和
五边形外角和=∠1+∠2+∠3+∠4+∠5
1、某人绕着课桌走一圈:
(1)每从课桌一边转到另一边时,身体转过的角是哪个角?会有多少度?
(2)每走完一圈,身体转过的角度之和是多少?
(为了更加直观,方便大家观察和思考这两个问题,请一位同学帮忙实景演示)
2、根据同学们的演示,老师将他走过的路线抽象成几何图形,如图所示。
∠1+∠2+∠3+∠4=?
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和.多边形的外角和又有怎样的规律呢?
6
情境创设
⌒
⌒
⌒
⌒
A
8
7
6
5
4
3
2
1
D
C
B
⌒
⌒
⌒
⌒
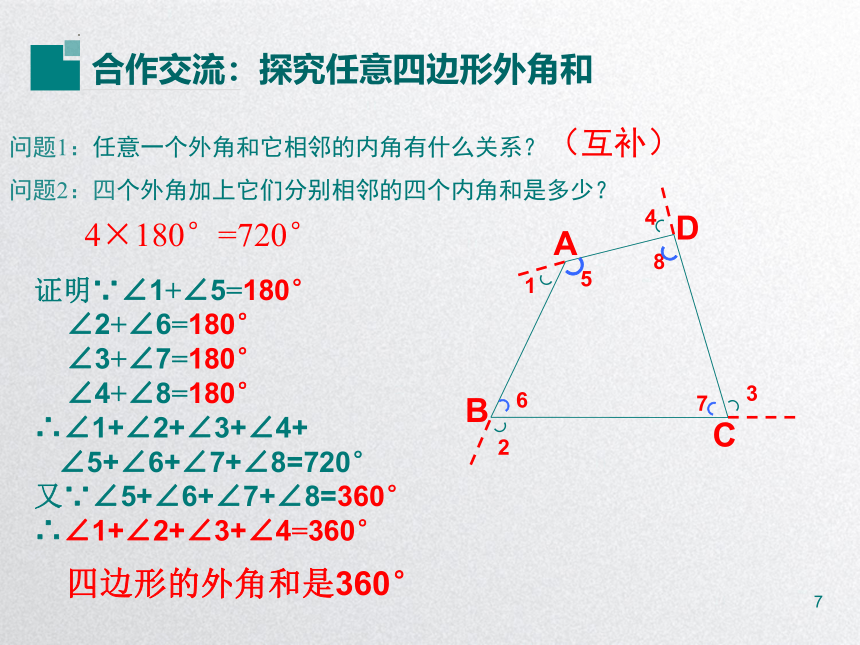
证明∵∠1+∠5=180°
∠2+∠6=180°
∠3+∠7=180°
∠4+∠8=180°
∴∠1+∠2+∠3+∠4+
∠5+∠6+∠7+∠8=720°
又∵∠5+∠6+∠7+∠8=360°
∴∠1+∠2+∠3+∠4=360°
四边形的外角和是360°
7
合作交流:探究任意四边形外角和
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:四个外角加上它们分别相邻的四个内角和是多少?
(互补)
4×180°=720°
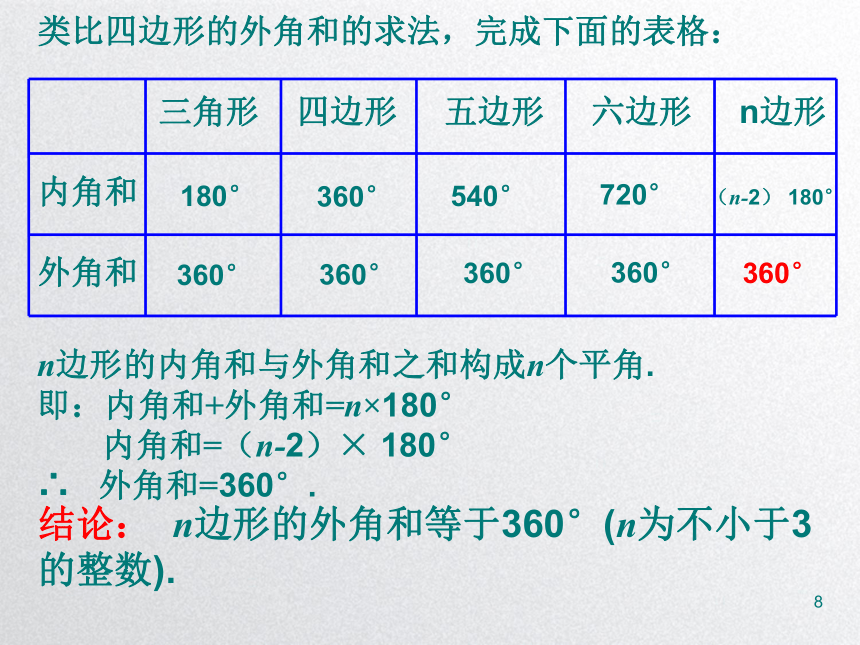
类比四边形的外角和的求法,完成下面的表格:
三角形 四边形 五边形 六边形 n边形
内角和
外角和
n边形的内角和与外角和之和构成n个平角.
即:内角和+外角和=n×180°
内角和=(n-2)× 180°
∴ 外角和=360°.
结论: n边形的外角和等于360°(n为不小于3的整数).
8
180°
360°
540°
720°
360°
360°
360°
360°
360°
(n-2) 180°
正多边形
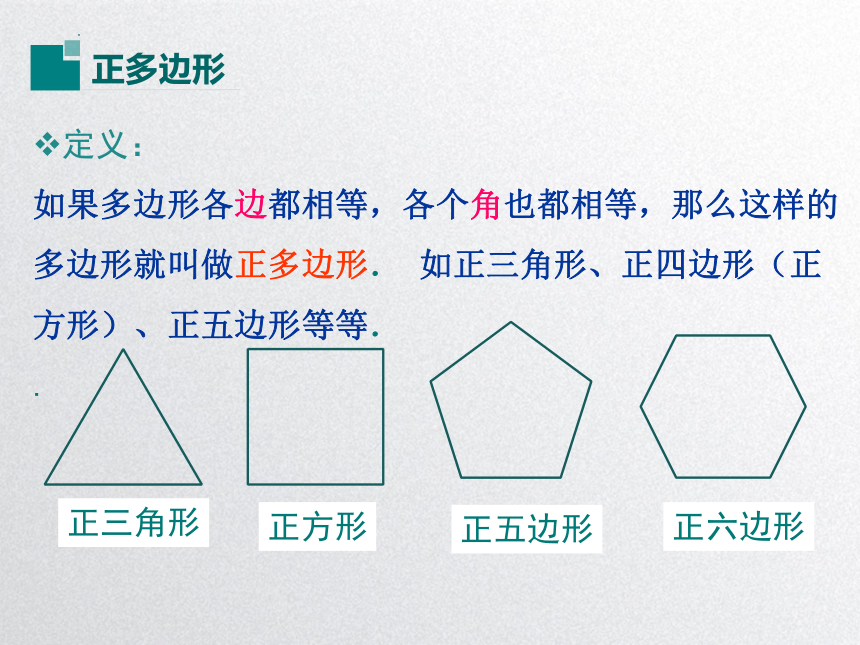
定义:
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形. 如正三角形、正四边形(正方形)、正五边形等等.
.
正三角形
正方形
正五边形
正六边形
因为正多边形的每个角相等,所以知道正多
边形的边数,就可以求出每一个内角的度数.
(n-2)×180°/ n
例1 求正六边形每个内角的度数和每个外角的度数.
解: 正六边形的内角和为
(6-2)×180°=720°
正六边形的外角和为360°
所以每个内角的度数为 720°÷ 6 = 120°
每个外角的度数为 360°÷ 6 = 60°
例2 正多边形的每个内角可能是:(1)75°;
(2)90°;(3)120°吗?说明理由.
答:不可能为75°,可能是90°或 120°.它们的外角分别是105°、90°、60°,360不能被105整除.
11
例题解析
例3 如果一个n边形的边数增加1,那么它的内角和增加多少度?外角和增加多少度?如果n边形的边数增加到原来的2倍,那么它的内角和增加多少度?外角和呢?
答:如果一个n边形的边数增加1,那么它的内角和增加180°,外角和增加0°.如果n边形的边数增加到原来的2倍,那么它的内角和增加n 180°外角和增加0°.
例4 小燕子从一点出发,沿着直线飞行10m后向左转30°,再沿着直线飞行10m,又向左转30°,……照这样走下去,她第一次回到出发地时,一共飞行了多少米?
答:120米。(360÷30×10=120)
12
我们都知道三角形具有稳定性,不容易变形.但四边形则具有不稳定性(即各边的长确定后,图形的形状不能确定).这种不稳定性在生活中有广泛的应用.如电动伸缩门(图1)、铁栅栏门(图2)、活动衣架(图3),
正是由于四边形可以变动,所以它可以拉开,也可以收拢.你能举出应用四边形的不稳定性的其他例子吗?
图1
图3
图2
13
四边形的不稳定性
1、任何一个凸多边形的内角中,为什么不能有3个以上的锐角?
答:假设一个凸多边形的内角中有4个或4个以上的内角是锐角,那么与这些锐角相邻的外角一定有4或4个个以上的钝角,这样它们的和就大于360°.那么这个多边形的外角和就一定大于360°.这与多边形的外角和等于360°相矛盾,因此,一个凸多边形的内角中,锐角的个数不能多于3个.
14
即时演练
2.(1)过四边形的一个顶点有 条对角线,四边形共有 条对角线;
(2)过五边形的一个顶点有 条对角线,五边形共有 条对角线;
(3)过n边形的一个顶点有 条对角线,n边形共有 条对角线;
n(n-3)/2
n-3
5
2
2
1
3. 一个凸多边形,除了一个内角外,其余各内角的和为 2750°,求这个多边形的边数以及除去的一个内角的度数.
设:边数为n(n≥3,n为正整数),除去内角为x°(0则180°(n-2)- x =2750°
n=17+( x +50)/180°
∵ x为多边形一个内角,n为正整数
∴ x =130°;n=18
15
课后思考:一个凸多边形的一个内角的补角与其他内角的和
恰好为500°,求这个多边形的边数?(5)
16
如下左图所示是二环三角形,可得S=∠A1+∠A2+…+∠A6=360°,如下中图是二环四边形,可得S=∠A1+∠A2+…+∠A8=720°,如下右图是二环五边形,可得S=1080°……聪明的同学,请根据以上规律直接写出二环n边形(n≥3的整数)中,S= 度(用含n的代数式表示)
(n-2) 360°
…
A6
A5
A4
A3
A2
A1
A6
A5
A4
A3
A2
A1
A9
A8
A7
A8
A10
A7
A6
A5
A4
A3
A2
A1
17
课例延伸
理由:连接A1A4
∵∠1+∠2+∠A1OA4=180°
∠A5+∠A6+∠A5OA6=180°
又∵∠A1OA4=∠A5OA6
∴∠1+∠2=∠A5+∠A6
∴∠A2+∠3+∠1+∠2+∠4+∠A3=360°
∴∠A2+∠3+∠A5+∠A6+∠4+∠A3=360°
即S=360°
解:(1)如图(2)所示,则S=∠A1+∠A2+…+∠A8=S=∠A1+∠A2+…+∠A5+∠M+∠1+∠2=(6-2)×180°=720°.
(2)依此类推,得是二环五边形时,则S=1080°;
推而广之,二环n边形(n≥3的整数)时,S=360(n-2).
分析:在(1)的基础上类似作辅助线,把要求的所有角转换到一个多边形中,再根据多边形的内角和定理进行求解.
点评:此题主要是巧妙构造辅助线把要求的角能够构造到一个多边形中.n边形的内角和是(n-2)×180°.
1、多边形的外角及外角和的定义;多边形的外角和定理;
2、利用多边形的内角和与外角和公式能解决以下问题:
(1)已知边数求内角和与内角度数;
(2)已知内角和求边数;
(3)已知各相等内角与外角度数求多边形边数。
3、正多边形相关概念及四边形的不稳定性;
4、在探求过程中我们使用了观察、归纳的数学方法,并且运用了类比、转化等数学思想。
课时小结
1、必做: 课本P74习题19.1 2、5
2、选做: 课本P74习题19.1 6
作业布置
感谢各位老师参与!
谢谢各位同学的配合!
《§19.1.2多边形外角和》
学习目标
1、经历多边形外角和的探究过程。
2、了解正多边形的定义并会用它解决问题。
3、了解四边形的不稳定性及在实际生活中的应用。
2
在平面内,由若干条不在同一条直线上的线段首尾顺次相接所组成的封闭图形,叫做多边形.组成多边形的线段叫做多边形的边;相邻两边的公共端点叫做多边形的顶点;多边形中相邻两条边组成的角叫做多边形的内角,简称多边形的角;在顶点处一边与另一边的延长线所组成的角叫做多边形的外角.多边形中连接不相邻两个顶点的线段,叫做多边形的对角线.
定理:n边形的内角和
等于(n-2) 180°
(n为不小于3的整数)
3
复习回顾
三角形
六边形
四边形
八边形
……
五边形
请画出下列图形从某一顶点出发的对角线的条数:
多边形 三角形 四边形 五边形 六边形 八边形 n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
0
1
2
3
5
n-3
1
2
3
4
6
n-2
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.
将多边形分成(n-2)个三角形. n(n≥3)边形共有n(n-3) /2条对角线
在顶点处多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
如图,∠1就叫做这个多边形的外角
E
B
C
D
1
2
3
4
5
A
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。多边形外角和不等于所有外角之和
五边形外角和=∠1+∠2+∠3+∠4+∠5
1、某人绕着课桌走一圈:
(1)每从课桌一边转到另一边时,身体转过的角是哪个角?会有多少度?
(2)每走完一圈,身体转过的角度之和是多少?
(为了更加直观,方便大家观察和思考这两个问题,请一位同学帮忙实景演示)
2、根据同学们的演示,老师将他走过的路线抽象成几何图形,如图所示。
∠1+∠2+∠3+∠4=?
在多边形的每个顶点处取多边形的一个外角,它们的和叫做多边形的外角和.多边形的外角和又有怎样的规律呢?
6
情境创设
⌒
⌒
⌒
⌒
A
8
7
6
5
4
3
2
1
D
C
B
⌒
⌒
⌒
⌒
证明∵∠1+∠5=180°
∠2+∠6=180°
∠3+∠7=180°
∠4+∠8=180°
∴∠1+∠2+∠3+∠4+
∠5+∠6+∠7+∠8=720°
又∵∠5+∠6+∠7+∠8=360°
∴∠1+∠2+∠3+∠4=360°
四边形的外角和是360°
7
合作交流:探究任意四边形外角和
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:四个外角加上它们分别相邻的四个内角和是多少?
(互补)
4×180°=720°
类比四边形的外角和的求法,完成下面的表格:
三角形 四边形 五边形 六边形 n边形
内角和
外角和
n边形的内角和与外角和之和构成n个平角.
即:内角和+外角和=n×180°
内角和=(n-2)× 180°
∴ 外角和=360°.
结论: n边形的外角和等于360°(n为不小于3的整数).
8
180°
360°
540°
720°
360°
360°
360°
360°
360°
(n-2) 180°
正多边形
定义:
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形. 如正三角形、正四边形(正方形)、正五边形等等.
.
正三角形
正方形
正五边形
正六边形
因为正多边形的每个角相等,所以知道正多
边形的边数,就可以求出每一个内角的度数.
(n-2)×180°/ n
例1 求正六边形每个内角的度数和每个外角的度数.
解: 正六边形的内角和为
(6-2)×180°=720°
正六边形的外角和为360°
所以每个内角的度数为 720°÷ 6 = 120°
每个外角的度数为 360°÷ 6 = 60°
例2 正多边形的每个内角可能是:(1)75°;
(2)90°;(3)120°吗?说明理由.
答:不可能为75°,可能是90°或 120°.它们的外角分别是105°、90°、60°,360不能被105整除.
11
例题解析
例3 如果一个n边形的边数增加1,那么它的内角和增加多少度?外角和增加多少度?如果n边形的边数增加到原来的2倍,那么它的内角和增加多少度?外角和呢?
答:如果一个n边形的边数增加1,那么它的内角和增加180°,外角和增加0°.如果n边形的边数增加到原来的2倍,那么它的内角和增加n 180°外角和增加0°.
例4 小燕子从一点出发,沿着直线飞行10m后向左转30°,再沿着直线飞行10m,又向左转30°,……照这样走下去,她第一次回到出发地时,一共飞行了多少米?
答:120米。(360÷30×10=120)
12
我们都知道三角形具有稳定性,不容易变形.但四边形则具有不稳定性(即各边的长确定后,图形的形状不能确定).这种不稳定性在生活中有广泛的应用.如电动伸缩门(图1)、铁栅栏门(图2)、活动衣架(图3),
正是由于四边形可以变动,所以它可以拉开,也可以收拢.你能举出应用四边形的不稳定性的其他例子吗?
图1
图3
图2
13
四边形的不稳定性
1、任何一个凸多边形的内角中,为什么不能有3个以上的锐角?
答:假设一个凸多边形的内角中有4个或4个以上的内角是锐角,那么与这些锐角相邻的外角一定有4或4个个以上的钝角,这样它们的和就大于360°.那么这个多边形的外角和就一定大于360°.这与多边形的外角和等于360°相矛盾,因此,一个凸多边形的内角中,锐角的个数不能多于3个.
14
即时演练
2.(1)过四边形的一个顶点有 条对角线,四边形共有 条对角线;
(2)过五边形的一个顶点有 条对角线,五边形共有 条对角线;
(3)过n边形的一个顶点有 条对角线,n边形共有 条对角线;
n(n-3)/2
n-3
5
2
2
1
3. 一个凸多边形,除了一个内角外,其余各内角的和为 2750°,求这个多边形的边数以及除去的一个内角的度数.
设:边数为n(n≥3,n为正整数),除去内角为x°(0
n=17+( x +50)/180°
∵ x为多边形一个内角,n为正整数
∴ x =130°;n=18
15
课后思考:一个凸多边形的一个内角的补角与其他内角的和
恰好为500°,求这个多边形的边数?(5)
16
如下左图所示是二环三角形,可得S=∠A1+∠A2+…+∠A6=360°,如下中图是二环四边形,可得S=∠A1+∠A2+…+∠A8=720°,如下右图是二环五边形,可得S=1080°……聪明的同学,请根据以上规律直接写出二环n边形(n≥3的整数)中,S= 度(用含n的代数式表示)
(n-2) 360°
…
A6
A5
A4
A3
A2
A1
A6
A5
A4
A3
A2
A1
A9
A8
A7
A8
A10
A7
A6
A5
A4
A3
A2
A1
17
课例延伸
理由:连接A1A4
∵∠1+∠2+∠A1OA4=180°
∠A5+∠A6+∠A5OA6=180°
又∵∠A1OA4=∠A5OA6
∴∠1+∠2=∠A5+∠A6
∴∠A2+∠3+∠1+∠2+∠4+∠A3=360°
∴∠A2+∠3+∠A5+∠A6+∠4+∠A3=360°
即S=360°
解:(1)如图(2)所示,则S=∠A1+∠A2+…+∠A8=S=∠A1+∠A2+…+∠A5+∠M+∠1+∠2=(6-2)×180°=720°.
(2)依此类推,得是二环五边形时,则S=1080°;
推而广之,二环n边形(n≥3的整数)时,S=360(n-2).
分析:在(1)的基础上类似作辅助线,把要求的所有角转换到一个多边形中,再根据多边形的内角和定理进行求解.
点评:此题主要是巧妙构造辅助线把要求的角能够构造到一个多边形中.n边形的内角和是(n-2)×180°.
1、多边形的外角及外角和的定义;多边形的外角和定理;
2、利用多边形的内角和与外角和公式能解决以下问题:
(1)已知边数求内角和与内角度数;
(2)已知内角和求边数;
(3)已知各相等内角与外角度数求多边形边数。
3、正多边形相关概念及四边形的不稳定性;
4、在探求过程中我们使用了观察、归纳的数学方法,并且运用了类比、转化等数学思想。
课时小结
1、必做: 课本P74习题19.1 2、5
2、选做: 课本P74习题19.1 6
作业布置
感谢各位老师参与!
谢谢各位同学的配合!
