2.3.2+两点之间的距离(课件含17页PPT)-【新教材精创】+2022-2023学年高二数学同步备课+(人教A版2019选择性+必修第一册)
文档属性
| 名称 | 2.3.2+两点之间的距离(课件含17页PPT)-【新教材精创】+2022-2023学年高二数学同步备课+(人教A版2019选择性+必修第一册) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 11:18:53 | ||
图片预览






文档简介
(共17张PPT)
高中数学 人教A版(2019) 选择性必修第一册
第二章 直线和圆的方程
2.3.2 两点之间的距离
教材分析
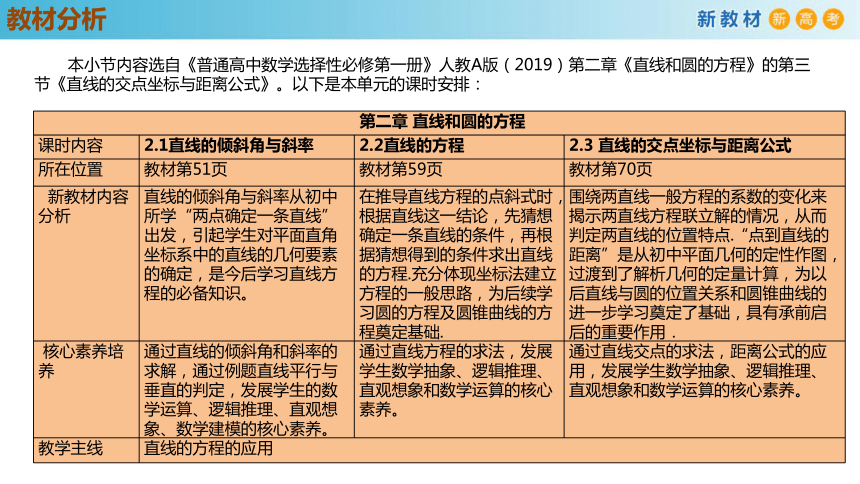
本小节内容选自《普通高中数学选择性必修第一册》人教A版(2019)第二章《直线和圆的方程》的第三节《直线的交点坐标与距离公式》。以下是本单元的课时安排:
第二章 直线和圆的方程 课时内容 2.1直线的倾斜角与斜率 2.2直线的方程 2.3 直线的交点坐标与距离公式
所在位置 教材第51页 教材第59页 教材第70页
新教材内容分析 直线的倾斜角与斜率从初中所学“两点确定一条直线”出发,引起学生对平面直角坐标系中的直线的几何要素的确定,是今后学习直线方程的必备知识。 在推导直线方程的点斜式时,根据直线这一结论,先猜想确定一条直线的条件,再根据猜想得到的条件求出直线的方程.充分体现坐标法建立方程的一般思路,为后续学习圆的方程及圆锥曲线的方程奠定基础. 围绕两直线一般方程的系数的变化来揭示两直线方程联立解的情况,从而判定两直线的位置特点.“点到直线的距离”是从初中平面几何的定性作图,过渡到了解析几何的定量计算,为以后直线与圆的位置关系和圆锥曲线的进一步学习奠定了基础,具有承前启后的重要作用.
核心素养培养 通过直线的倾斜角和斜率的求解,通过例题直线平行与垂直的判定,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。 通过直线方程的求法,发展学生数学抽象、逻辑推理、直观想象和数学运算的核心素养。 通过直线交点的求法,距离公式的应用,发展学生数学抽象、逻辑推理、直观想象和数学运算的核心素养。
教学主线 直线的方程的应用 学习目标
1.掌握平面上两点间的距离公式,提升数学运算的核心素养.
2.会运用坐标法证明简单的平面几何问题,培养逻辑推理的核心素养.
重点、难点
重点:平面上两点间的距离公式的推导与应用
难点:运用坐标法证明简单的平面几何问题
(一)新知导入
在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小
(二)两点之间的距离
【探究】1.已知两点P1(x1,y1),P2(x2,y2),那么向量的坐标是什么?
【提示】=(x2-x1,y2-y1).
2.根据向量的模的计算公式,你能得到||的公式吗?
【提示】 ||=.
向量的模就是向量两个端点之间的距离。
(二)两点之间的距离
◆ (1)平面内两点P1(x1,y1),P2(x2,y2)间的距离公式|P1P2|= .
文字叙述:平面内两点的距离等于这两点的横坐标之差与纵坐标之差的 的算术平方根.
(2)两点间距离的特殊情况
①原点O(0,0)与任一点P(x,y)的距离|OP|= .
②当P1P2∥x轴(y1=y2)时,|P1P2|= .
③当P1P2∥y轴(x1=x2)时,|P1P2|= .
【做一做1】 (教材P74练习1改编)已知M(2,1),N(-1,5),则|MN|等于( )
A.5 B. C. D.4
【答案】A
注意:公式中两点的位置没有先后之分
平方和
|x2-x1|
|y2-y1|
(三)典型例题
1.两点之间距离公式的应用
例1.已知△ABC三个顶点的坐标分别为A(-3,1),B(3,-3),C(1,7),试判断△ABC的形状.
【解析】法一:∵|AB|==,
|AC|==,
又|BC|==,
∴AB2+AC2=BC2,且AB=AC,
∴△ABC是等腰直角三角形.
法二:∵kAC==,kAB==,
则kAC·kAB=-1,∴AC⊥AB.
又|AC|=
,
|AB|=
,
∴AC=AB.
∴△ABC是等腰直角三角形.
(三)典型例题
例2. 在直线l:3x-y+1=0上求一点P,使点P到两点A(1,-1),B(2,0)的距离相等.
【解析】 法一:设P点坐标为(x,y),
由P在l上和P到A,B距离相等建立方程组
解得
∴P点坐标为(0,1).
法二:设P(x,y),两点A(1,-1),B(2,0)连线所得线段的中垂线方程为x+y-1=0,①
又3x-y+1=0,②
解由①②组成的方程组
得, 所以所求的点为P(0,1).
(三)典型例题
【类题通法】两点间的距离公式是解析几何的重要公式之一,它主要解决线段的长度问题,体现了数形结合思想的应用.
【巩固练习1】已知点A(4,12),P为x轴上的一点,且点P与点A的距离等于13,则点P的坐标为______.
解析:设点P的坐标为(x,0),
由|PA|=13,得=13,解得x=-1或x=9.
所以点P的坐标为(-1,0)或(9,0).
答案:(-1,0)或(9,0)
(三)典型例题
2.坐标法的应用
例3. 如图,在△ABC中,|AB|=|AC|,D是BC边上异于B,C的任意一点,
求证:|AB|2=|AD|2+|BD|·|DC|.
【证明】如图,以BC的中点为原点O,BC所在的直线为x轴,建立直角坐标系.
设A(0,a),B(-b,0),C(b,0),D(m,0)(-b则|AB|2=(-b-0)2+(0-a)2=a2+b2,
|AD|2=(m-0)2+(0-a)2=m2+a2,
|BD|·|DC|=|m+b|·|b-m|=(b+m)(b-m)=b2-m2,
∴|AD|2+|BD|·|DC|=a2+b2,
∴|AB|2=|AD|2+|BD|·|DC|.
(三)典型例题
【类题通法】 坐标法及其应用
1.坐标法解决几何问题时,关键要结合图形的特征,建立平面直角坐标系.坐标系建立的是否合适,会直接影响问题能否方便解决.建系的原则主要有两点:
(1)让尽可能多的点落在坐标轴上,这样便于运算;
(2)如果条件中有互相垂直的两条线,要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果有轴对称性,可考虑将对称轴作为坐标轴.
2.利用坐标法解平面几何问题常见的步骤:
(1)建立坐标系,尽可能将有关元素放在坐标轴上;
(2)用坐标表示有关的量;
(3)将几何关系转化为坐标运算;
(4)把代数运算结果“翻译”成几何关系.
(三)典型例题
【巩固练习2】已知正三角形ABC的边长为a,在平面ABC上求一点P,使|PA|2+|PB|2+|PC|2最小,并求此最小值.
【解析】以BC所在直线为x轴,以线段BC的中点为原点,建立直角坐标系,如图所示.
∵正三角形ABC的边长为a,
∴BC, A.设P(x,y),由两点间的距离公式,得
|PA|2+|PB|2+|PC|2=x2+(y- a)2+(x+)2+y2+(x- )2+y2
=3x2+3y2 - ay+=3x2+3(y- a)2+a2≥a2,
当且仅当x=0,y=a时,等号成立,
故所求最小值为a2,此时点P的坐标为(0, a).
(四)操作演练 素养提升
1.设点A在x轴上,点B在y轴上,线段AB的中点P(2,-1),则|AB|=( )
A.2 B.4 C.5 D.2
2.已知△ABC的顶点A(2,3),B(-1,0),C(2,0),则△ABC的周长是( )
A.2 B.3+2C.6+3 D.6+
3.已知△ABC的三个顶点是A(-a,0),B(a,0)和C,则△ABC的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.斜三角形
4.已知点A(x,5)关于点(1,y)的对称点为(-2,-3),则点P(x,y)到原点的距离是( )
A.2 B.4 C.5 D.
答案:1.A 2.C 3.C 4.D
(五)课堂小结
知识总结
学生反思
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
作业布置
完成教材—— 第74页 练习 第1,2,3题
第79页 习题2.3 第5,12题
不积跬步,无以至千里;
不积小流,无以成江海。
谢 谢 ~~
高中数学 人教A版(2019) 选修第一册
高中数学 人教A版(2019) 选择性必修第一册
第二章 直线和圆的方程
2.3.2 两点之间的距离
教材分析
本小节内容选自《普通高中数学选择性必修第一册》人教A版(2019)第二章《直线和圆的方程》的第三节《直线的交点坐标与距离公式》。以下是本单元的课时安排:
第二章 直线和圆的方程 课时内容 2.1直线的倾斜角与斜率 2.2直线的方程 2.3 直线的交点坐标与距离公式
所在位置 教材第51页 教材第59页 教材第70页
新教材内容分析 直线的倾斜角与斜率从初中所学“两点确定一条直线”出发,引起学生对平面直角坐标系中的直线的几何要素的确定,是今后学习直线方程的必备知识。 在推导直线方程的点斜式时,根据直线这一结论,先猜想确定一条直线的条件,再根据猜想得到的条件求出直线的方程.充分体现坐标法建立方程的一般思路,为后续学习圆的方程及圆锥曲线的方程奠定基础. 围绕两直线一般方程的系数的变化来揭示两直线方程联立解的情况,从而判定两直线的位置特点.“点到直线的距离”是从初中平面几何的定性作图,过渡到了解析几何的定量计算,为以后直线与圆的位置关系和圆锥曲线的进一步学习奠定了基础,具有承前启后的重要作用.
核心素养培养 通过直线的倾斜角和斜率的求解,通过例题直线平行与垂直的判定,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。 通过直线方程的求法,发展学生数学抽象、逻辑推理、直观想象和数学运算的核心素养。 通过直线交点的求法,距离公式的应用,发展学生数学抽象、逻辑推理、直观想象和数学运算的核心素养。
教学主线 直线的方程的应用 学习目标
1.掌握平面上两点间的距离公式,提升数学运算的核心素养.
2.会运用坐标法证明简单的平面几何问题,培养逻辑推理的核心素养.
重点、难点
重点:平面上两点间的距离公式的推导与应用
难点:运用坐标法证明简单的平面几何问题
(一)新知导入
在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小
(二)两点之间的距离
【探究】1.已知两点P1(x1,y1),P2(x2,y2),那么向量的坐标是什么?
【提示】=(x2-x1,y2-y1).
2.根据向量的模的计算公式,你能得到||的公式吗?
【提示】 ||=.
向量的模就是向量两个端点之间的距离。
(二)两点之间的距离
◆ (1)平面内两点P1(x1,y1),P2(x2,y2)间的距离公式|P1P2|= .
文字叙述:平面内两点的距离等于这两点的横坐标之差与纵坐标之差的 的算术平方根.
(2)两点间距离的特殊情况
①原点O(0,0)与任一点P(x,y)的距离|OP|= .
②当P1P2∥x轴(y1=y2)时,|P1P2|= .
③当P1P2∥y轴(x1=x2)时,|P1P2|= .
【做一做1】 (教材P74练习1改编)已知M(2,1),N(-1,5),则|MN|等于( )
A.5 B. C. D.4
【答案】A
注意:公式中两点的位置没有先后之分
平方和
|x2-x1|
|y2-y1|
(三)典型例题
1.两点之间距离公式的应用
例1.已知△ABC三个顶点的坐标分别为A(-3,1),B(3,-3),C(1,7),试判断△ABC的形状.
【解析】法一:∵|AB|==,
|AC|==,
又|BC|==,
∴AB2+AC2=BC2,且AB=AC,
∴△ABC是等腰直角三角形.
法二:∵kAC==,kAB==,
则kAC·kAB=-1,∴AC⊥AB.
又|AC|=
,
|AB|=
,
∴AC=AB.
∴△ABC是等腰直角三角形.
(三)典型例题
例2. 在直线l:3x-y+1=0上求一点P,使点P到两点A(1,-1),B(2,0)的距离相等.
【解析】 法一:设P点坐标为(x,y),
由P在l上和P到A,B距离相等建立方程组
解得
∴P点坐标为(0,1).
法二:设P(x,y),两点A(1,-1),B(2,0)连线所得线段的中垂线方程为x+y-1=0,①
又3x-y+1=0,②
解由①②组成的方程组
得, 所以所求的点为P(0,1).
(三)典型例题
【类题通法】两点间的距离公式是解析几何的重要公式之一,它主要解决线段的长度问题,体现了数形结合思想的应用.
【巩固练习1】已知点A(4,12),P为x轴上的一点,且点P与点A的距离等于13,则点P的坐标为______.
解析:设点P的坐标为(x,0),
由|PA|=13,得=13,解得x=-1或x=9.
所以点P的坐标为(-1,0)或(9,0).
答案:(-1,0)或(9,0)
(三)典型例题
2.坐标法的应用
例3. 如图,在△ABC中,|AB|=|AC|,D是BC边上异于B,C的任意一点,
求证:|AB|2=|AD|2+|BD|·|DC|.
【证明】如图,以BC的中点为原点O,BC所在的直线为x轴,建立直角坐标系.
设A(0,a),B(-b,0),C(b,0),D(m,0)(-b
|AD|2=(m-0)2+(0-a)2=m2+a2,
|BD|·|DC|=|m+b|·|b-m|=(b+m)(b-m)=b2-m2,
∴|AD|2+|BD|·|DC|=a2+b2,
∴|AB|2=|AD|2+|BD|·|DC|.
(三)典型例题
【类题通法】 坐标法及其应用
1.坐标法解决几何问题时,关键要结合图形的特征,建立平面直角坐标系.坐标系建立的是否合适,会直接影响问题能否方便解决.建系的原则主要有两点:
(1)让尽可能多的点落在坐标轴上,这样便于运算;
(2)如果条件中有互相垂直的两条线,要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果有轴对称性,可考虑将对称轴作为坐标轴.
2.利用坐标法解平面几何问题常见的步骤:
(1)建立坐标系,尽可能将有关元素放在坐标轴上;
(2)用坐标表示有关的量;
(3)将几何关系转化为坐标运算;
(4)把代数运算结果“翻译”成几何关系.
(三)典型例题
【巩固练习2】已知正三角形ABC的边长为a,在平面ABC上求一点P,使|PA|2+|PB|2+|PC|2最小,并求此最小值.
【解析】以BC所在直线为x轴,以线段BC的中点为原点,建立直角坐标系,如图所示.
∵正三角形ABC的边长为a,
∴BC, A.设P(x,y),由两点间的距离公式,得
|PA|2+|PB|2+|PC|2=x2+(y- a)2+(x+)2+y2+(x- )2+y2
=3x2+3y2 - ay+=3x2+3(y- a)2+a2≥a2,
当且仅当x=0,y=a时,等号成立,
故所求最小值为a2,此时点P的坐标为(0, a).
(四)操作演练 素养提升
1.设点A在x轴上,点B在y轴上,线段AB的中点P(2,-1),则|AB|=( )
A.2 B.4 C.5 D.2
2.已知△ABC的顶点A(2,3),B(-1,0),C(2,0),则△ABC的周长是( )
A.2 B.3+2C.6+3 D.6+
3.已知△ABC的三个顶点是A(-a,0),B(a,0)和C,则△ABC的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.斜三角形
4.已知点A(x,5)关于点(1,y)的对称点为(-2,-3),则点P(x,y)到原点的距离是( )
A.2 B.4 C.5 D.
答案:1.A 2.C 3.C 4.D
(五)课堂小结
知识总结
学生反思
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
作业布置
完成教材—— 第74页 练习 第1,2,3题
第79页 习题2.3 第5,12题
不积跬步,无以至千里;
不积小流,无以成江海。
谢 谢 ~~
高中数学 人教A版(2019) 选修第一册
