北师大版数学八年级上册 第一章勾股定理——最短路径问题训练(word、含答案)
文档属性
| 名称 | 北师大版数学八年级上册 第一章勾股定理——最短路径问题训练(word、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 19:59:54 | ||
图片预览

文档简介
北师大版数学八年级上册
第一章勾股定理——最短路径问题训练一
一、选择题
如图,透明的圆柱形玻璃容器容器厚度忽略不计的高为,在容器内壁离容器底部的点处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿的点处,若蚂蚁吃到蜂蜜需爬行的最短路径为,则该圆柱底面周长为.( )
A. B. C. D.
如图,圆柱的底面周长为,是底面圆的直径,高,点是上一点,且一只蚂蚁从点出发沿着圆柱体的表面爬行到点的最短路程是( )
A. B. C. D.
如图,点和点分别是棱长为的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由处向处爬行,所走的最短路程是( )
A.
B.
C.
D.
如图,有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点处有一只蚂蚁,它想吃到上底面与点相对的点处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
B.
C.
D.
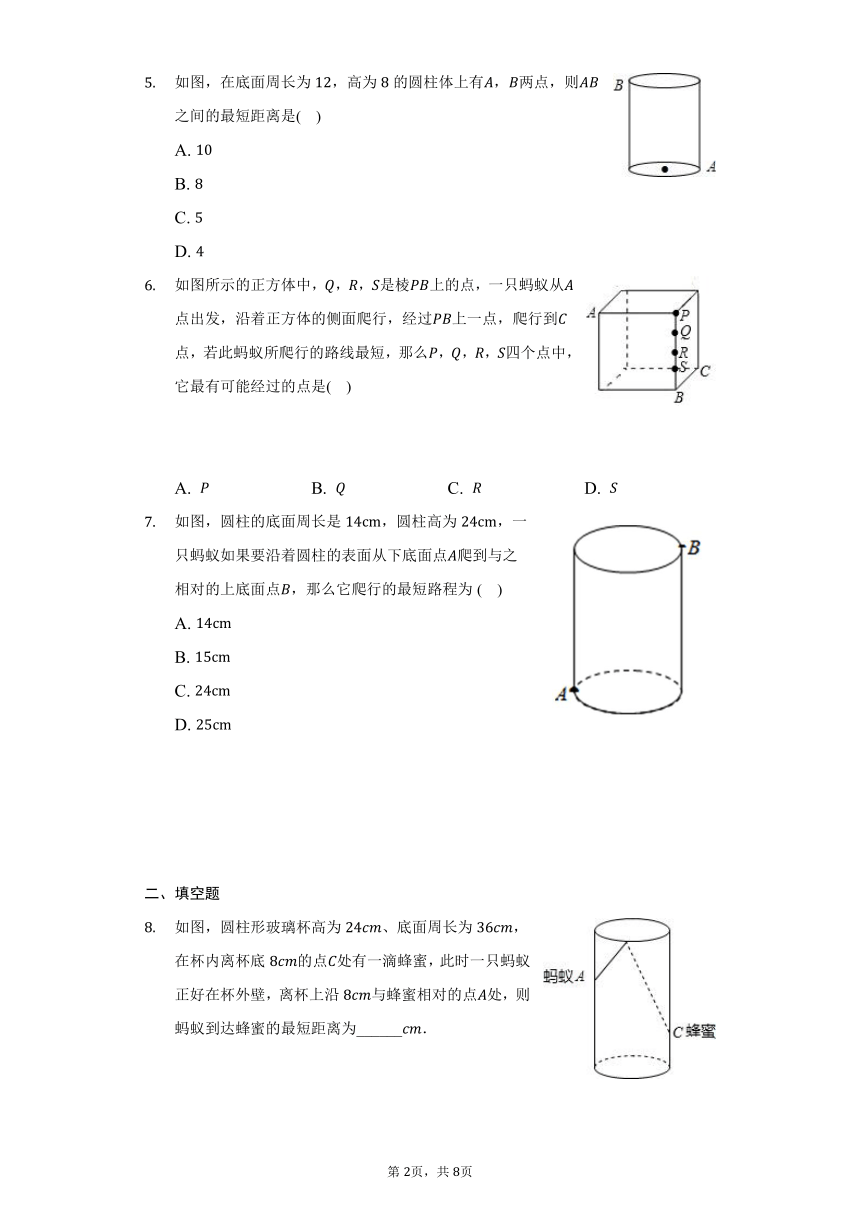
如图,在底面周长为,高为的圆柱体上有,两点,则之间的最短距离是( )
A.
B.
C.
D.
如图所示的正方体中,,,是棱上的点,一只蚂蚁从点出发,沿着正方体的侧面爬行,经过上一点,爬行到点,若此蚂蚁所爬行的路线最短,那么,,,四个点中,它最有可能经过的点是( )
A. B. C. D.
如图,圆柱的底面周长是,圆柱高为,一只蚂蚁如果要沿着圆柱的表面从下底面点爬到与之相对的上底面点,那么它爬行的最短路程为( )
A.
B.
C.
D.
二、填空题
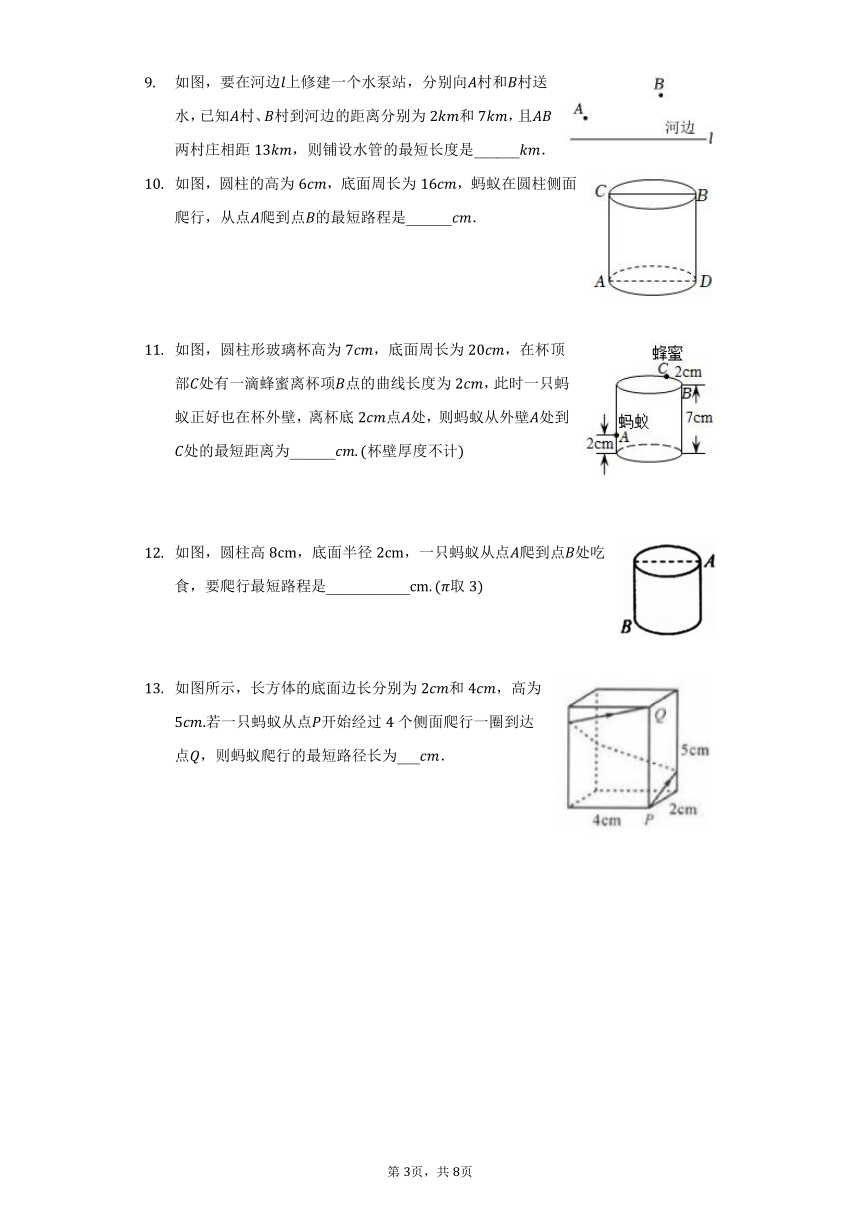
如图,圆柱形玻璃杯高为、底面周长为,在杯内离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁到达蜂蜜的最短距离为______.
如图,要在河边上修建一个水泵站,分别向村和村送水,已知村、村到河边的距离分别为和,且两村庄相距,则铺设水管的最短长度是______.
如图,圆柱的高为,底面周长为,蚂蚁在圆柱侧面爬行,从点爬到点的最短路程是______.
如图,圆柱形玻璃杯高为,底面周长为,在杯顶部处有一滴蜂蜜离杯项点的曲线长度为,此时一只蚂蚁正好也在杯外壁,离杯底点处,则蚂蚁从外壁处到处的最短距离为______杯壁厚度不计
如图,圆柱高,底面半径,一只蚂蚁从点爬到点处吃食,要爬行最短路程是___________取
如图所示,长方体的底面边长分别为和,高为若一只蚂蚁从点开始经过个侧面爬行一圈到达点,则蚂蚁爬行的最短路径长为___.
三、解答题
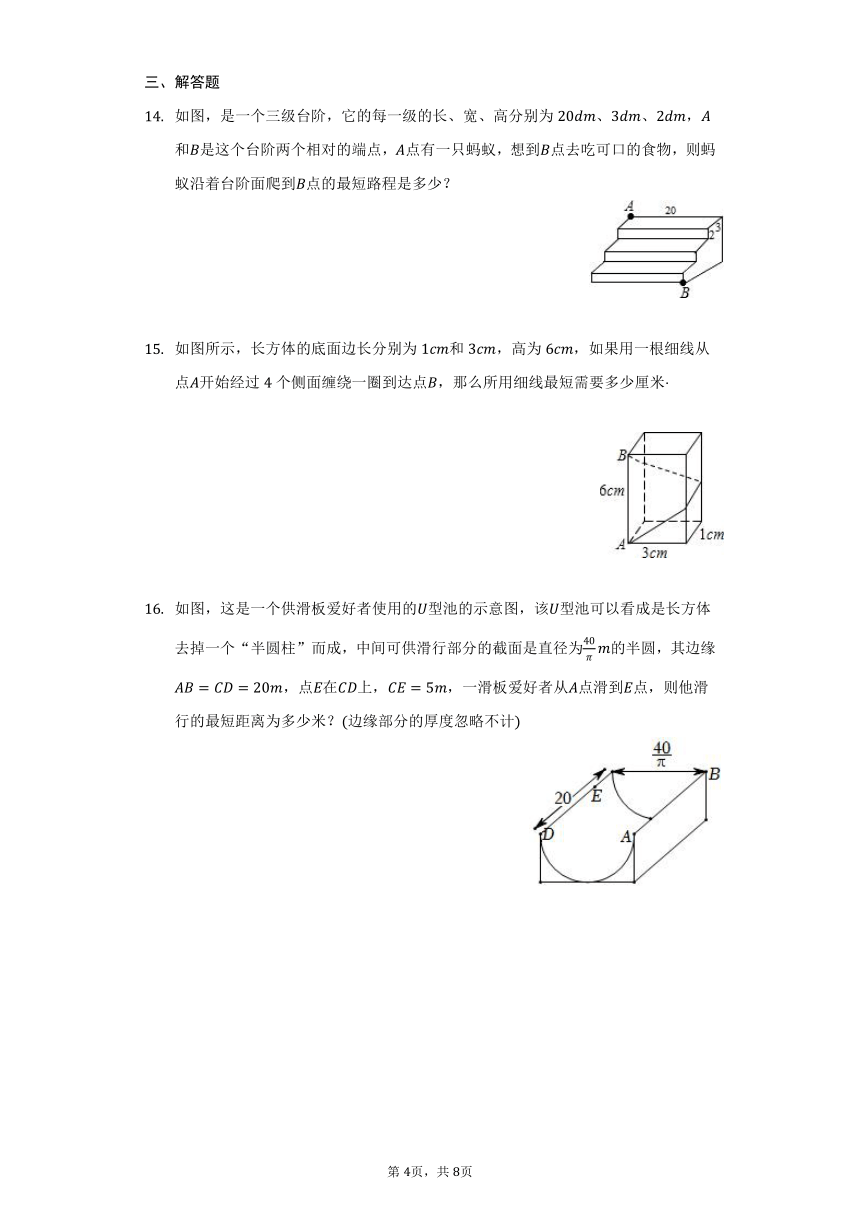
如图,是一个三级台阶,它的每一级的长、宽、高分别为、、,和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点的最短路程是多少?
如图所示,长方体的底面边长分别为和,高为,如果用一根细线从点开始经过个侧面缠绕一圈到达点,那么所用细线最短需要多少厘米
如图,这是一个供滑板爱好者使用的型池的示意图,该型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点在上,,一滑板爱好者从点滑到点,则他滑行的最短距离为多少米?边缘部分的厚度忽略不计
如图是一个三级台阶,每级台阶都是长、宽和高分别等于,和的长方体,和是这个台阶的两个相对的端点.在点处有一只蚂蚁,想到点去吃可口的食物,请你算一算,这只蚂蚁从点出发,沿着台阶面爬到点,最短路程是多少?
如图所示,圆柱形容器高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,求蚂蚁从外壁处到达内壁处的最短距离.
如图,河同侧有一块直角三角形的绿化带,,,,到河的距离等于的长度.需要用水管从河上一点处分别引水到,两处,并通过安装在这两处的喷水龙头灌溉草地.
请在河上画出点的位置,使得从点向,两处引水所需的水管总长度最短;
求至少需要水管多少米连接处接头长度忽略不计.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:三级台阶平面展开图为长方形,长为,宽为,
则蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到点最短路程为,
由勾股定理得:,
解得:.
答:蚂蚁沿着台阶面爬到点的最短路程是.
15.解:将长方体展开,连接,
,,
根据两点之间线段最短,.
故所用细线最短需要厘米
16.解:如图是其侧面展开图:,,
在中,.
故他滑行的最短距离约为.
17.解:展开后由题意得:,,,
由勾股定理得:,
答:最短路程是.
18.解:如图,将杯子侧面展开,作关于的对称点,连接,作交的延长线于点,
则的长即为最短距离,
,,
,
蚂蚁从外壁处到达内壁处的最短距离是.
19.解:如图,点即为所求;
,,
,,在同一条直线上,
,,
,,
,
,
,
,
米,
答:至少需要水管米.
第2页,共2页
第1页,共1页
第一章勾股定理——最短路径问题训练一
一、选择题
如图,透明的圆柱形玻璃容器容器厚度忽略不计的高为,在容器内壁离容器底部的点处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿的点处,若蚂蚁吃到蜂蜜需爬行的最短路径为,则该圆柱底面周长为.( )
A. B. C. D.
如图,圆柱的底面周长为,是底面圆的直径,高,点是上一点,且一只蚂蚁从点出发沿着圆柱体的表面爬行到点的最短路程是( )
A. B. C. D.
如图,点和点分别是棱长为的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由处向处爬行,所走的最短路程是( )
A.
B.
C.
D.
如图,有一个圆柱,它的高等于,底面上圆的周长等于,在圆柱下底面的点处有一只蚂蚁,它想吃到上底面与点相对的点处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
B.
C.
D.
如图,在底面周长为,高为的圆柱体上有,两点,则之间的最短距离是( )
A.
B.
C.
D.
如图所示的正方体中,,,是棱上的点,一只蚂蚁从点出发,沿着正方体的侧面爬行,经过上一点,爬行到点,若此蚂蚁所爬行的路线最短,那么,,,四个点中,它最有可能经过的点是( )
A. B. C. D.
如图,圆柱的底面周长是,圆柱高为,一只蚂蚁如果要沿着圆柱的表面从下底面点爬到与之相对的上底面点,那么它爬行的最短路程为( )
A.
B.
C.
D.
二、填空题
如图,圆柱形玻璃杯高为、底面周长为,在杯内离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁到达蜂蜜的最短距离为______.
如图,要在河边上修建一个水泵站,分别向村和村送水,已知村、村到河边的距离分别为和,且两村庄相距,则铺设水管的最短长度是______.
如图,圆柱的高为,底面周长为,蚂蚁在圆柱侧面爬行,从点爬到点的最短路程是______.
如图,圆柱形玻璃杯高为,底面周长为,在杯顶部处有一滴蜂蜜离杯项点的曲线长度为,此时一只蚂蚁正好也在杯外壁,离杯底点处,则蚂蚁从外壁处到处的最短距离为______杯壁厚度不计
如图,圆柱高,底面半径,一只蚂蚁从点爬到点处吃食,要爬行最短路程是___________取
如图所示,长方体的底面边长分别为和,高为若一只蚂蚁从点开始经过个侧面爬行一圈到达点,则蚂蚁爬行的最短路径长为___.
三、解答题
如图,是一个三级台阶,它的每一级的长、宽、高分别为、、,和是这个台阶两个相对的端点,点有一只蚂蚁,想到点去吃可口的食物,则蚂蚁沿着台阶面爬到点的最短路程是多少?
如图所示,长方体的底面边长分别为和,高为,如果用一根细线从点开始经过个侧面缠绕一圈到达点,那么所用细线最短需要多少厘米
如图,这是一个供滑板爱好者使用的型池的示意图,该型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为的半圆,其边缘,点在上,,一滑板爱好者从点滑到点,则他滑行的最短距离为多少米?边缘部分的厚度忽略不计
如图是一个三级台阶,每级台阶都是长、宽和高分别等于,和的长方体,和是这个台阶的两个相对的端点.在点处有一只蚂蚁,想到点去吃可口的食物,请你算一算,这只蚂蚁从点出发,沿着台阶面爬到点,最短路程是多少?
如图所示,圆柱形容器高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,求蚂蚁从外壁处到达内壁处的最短距离.
如图,河同侧有一块直角三角形的绿化带,,,,到河的距离等于的长度.需要用水管从河上一点处分别引水到,两处,并通过安装在这两处的喷水龙头灌溉草地.
请在河上画出点的位置,使得从点向,两处引水所需的水管总长度最短;
求至少需要水管多少米连接处接头长度忽略不计.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:三级台阶平面展开图为长方形,长为,宽为,
则蚂蚁沿台阶面爬行到点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到点最短路程为,
由勾股定理得:,
解得:.
答:蚂蚁沿着台阶面爬到点的最短路程是.
15.解:将长方体展开,连接,
,,
根据两点之间线段最短,.
故所用细线最短需要厘米
16.解:如图是其侧面展开图:,,
在中,.
故他滑行的最短距离约为.
17.解:展开后由题意得:,,,
由勾股定理得:,
答:最短路程是.
18.解:如图,将杯子侧面展开,作关于的对称点,连接,作交的延长线于点,
则的长即为最短距离,
,,
,
蚂蚁从外壁处到达内壁处的最短距离是.
19.解:如图,点即为所求;
,,
,,在同一条直线上,
,,
,,
,
,
,
,
米,
答:至少需要水管米.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
