北师大版八年级上册 5二元一次方程组单元复习课件(共35张PPT)
文档属性
| 名称 | 北师大版八年级上册 5二元一次方程组单元复习课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 231.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 09:35:35 | ||
图片预览









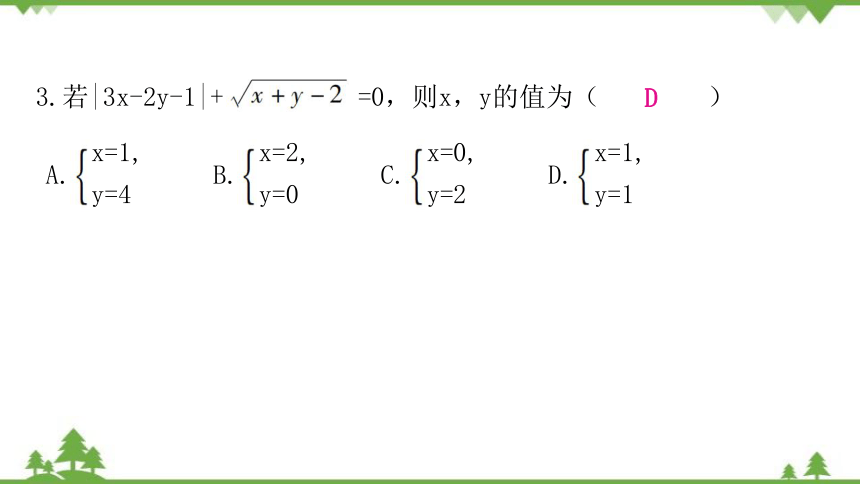


文档简介
(共35张PPT)
第五章 二元一次方程组
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.掌握代入消元法和加减消元法,能解二元一次方程组.
2.能根据具体问题的实际意义,检验方程的解是否合理.
3.体会一次函数与二元一次方程的关系.
知识导航
二元一次 方程组 基本概念 二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程.
二元一次方程的解:适合一个二元一次方程的一组未知数的值
二元一次方程组:共含有两个未知数的两个一次方程所组成的一组方程.
二元一次方程组的解:二元一次方程中各个方程的公共解
续表
二元一次 方程组 基本解法 代入消元法:将二元一次方程组其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程,从而消去一个未知数的解方程组的方法
加减消元法:将二元一次方程组的两个方程变形后,通过两式相加(减)消去其中一个未知数的解方程组的方法
续表
二元一次 方程组 实际应用 类型:鸡兔同笼、增收节支、里程碑上的数
二元一次方程(组)与一次函数的关系 1.方程的解与函数图象上的点的坐标一一对应;
2.两条直线的交点坐标就是相应的二元一次方程组的解,反之亦然
续表
二元一次 方程组 三元一次 方程组 三元一次方程:含有三个未知数,并且所含未知数的项的次数都是1的方程
三元一次方程组:共含有三个未知数的三个一次方程所组成的一组方程
三元一次方程组的解:三元一次方程中各个方程的公共解
三元一次方程组的解法:代入消元法、加减消元法
专题1 求解二元一次方程组
1.已知方程组 则x-y的值为( )
A. B.2 C.3 D.-2
2x+y=4,
x+2y=1
C
2. (2020牡丹江)若 是二元一次方程组
的解,则x+2y的算术平方根为( )
A. 3 B. ±3 C. D.±
a=2
b=1
ax+by=5
ax-by=2
C
3.若|3x-2y-1|+ =0,则x,y的值为( )
A.
x=1,
y=4
B.
x=2,
y=0
C.
x=0,
y=2
D.
x=1,
y=1
D
4. (2020南京)已知x,y满足方程组 则x+y的值为
_________.
x+3y=-1,
2x+y=3,
1
5. 解方程组:
x+y=1,
4x+y=10.
解:
②-①,得3x=9.
解得x=3.
把x=3代入①,得y=-2.
则原方程组的解为
x+y=1,①
4x+y=10.②
x=3,
y=-2.
6. 解方程组:
x+2y=0,
3x+4y=6.
解:
①×2-②,得-x=-6.
解得x=6.
将x=6代入①,得6+2y=0.
解得y=-3.
故原方程组的解为
x+2y=0,①
3x+4y=6.②
x=6,
y=-3.
7. (2020佛山)解方程组:
=2,
3(2x+1)-2(4y-3)=5.
解:设 =m, =n,将原方程组化为
①×4+②,得13m=13.解得m=1.
把m=1代入①,得n=1,即 =1, =1.
解得x=1,y=
所以原方程组的解为
m+n=2,①,
9m-4n=5.②
x=1,
y=
8. (2020陕西)已知方程组 和方程组
的解相同,试判断点P(a,b)在第几象限.
2x+y=-2,
ax-by=-4
3x-y=12,
bx+ay=-8
解:由2x+y=-2和3x-y=12组成方程组,解得
代入 得
解得
所以点P(1,-1)在第四象限.
x=2,
y=-6,
ax-by=-4,
bx+ay=-8,
2a+6b=-4,
2b-6a=-8,
a=1,
b=-1.
9. 已知两个方程组 和 有公共解,求a,b的值.
2x+y=5,
ax-by=-4
5x-4y=6,
2ax+3by=2
代入第二组方程组,得
解得
2a-b=-4,
4a+3b=2.
a=-1,
b=2.
解:因为方程组 和 有公共解,
所以原方程组可化为 和
由第一组方程组解得
2x+y=5,
ax-by=-4
5x-4y=6,
2ax+3by=2
2x+y=5,
5x-4y=6
ax-by=-4,
2ax+3by=2.
x=2,
y=1.
1.某出租车起步价所包含的路程为0~2 km,超过2 km的部分按每千米另收费.津津乘坐这种出租车行了7 km,付了16元;盼盼乘坐这种出租车行了13 km,付了28元.设这种出租车的起步价为x元,超过2 km后每千米收费y元,则下面所列方程组正确的是( )
专题2 应用二元一次方程组
D
A.
x+7y=16,
x+13y=28
B.
x+(7-2)y=16,
x+13y=28
C.
x+7y=16,
x+(13-2)y=28
D.
x+(7-2)y=16,
x+(13-2)y=28
2. (2020龙东)学校计划用200元钱购买A,B两种奖品,A种每个15元,B种每个25元,在钱全部用完的情况下,有多少种购买方案?( )
A. 2种 B. 3种
C. 4种 D.5种
B
3. 如图Z5-1所示的两台天平保持平衡,已知每块巧克力的重量相等,每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )
A.10 g,40 g B.15 g,35 g
C.20 g,30 g D.30 g,20 g
C
4. 如图Z5-2,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A.35
B.45
C.55
D.65
B
5. (2020常德)今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是_________次.
4
6.某活动小组购买了4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意可列方程组为
__________________.
x-y=4,
4x+5y=466
7. 用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品.要生产甲种产品37件,乙种产品18件,则恰好需用A,B两种型号的钢板共_________块.
11
8. 某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年元旦期间的销售情况,下面是调查后小明与其他两位同学进行交流的情景.
小明说:“去年两家超市的销售额共为150万元,今年两家超市的销售额共为170万元.”
小亮说:“甲超市今年的销售额比去年增加10%.”
小颖说:“乙超市今年的销售额比去年增加20%.”
根据他们的对话,得出今年甲超市的销售额为_________万元.
110
9. (2020合肥)如图Z5-3所示是正方体的表面展开图,若正方体相对的两个面上的数或式子的值相等,求x和y的值.
解:由题意可列方程组为
解得
x-3=2y,
2x-1=y+2.
x=1,
y=-1.
地点 售价
历史博物馆 10元/人
民俗展览馆 20元/人
10. 本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆.每一名学生只能参加其中一项活动,共支付票款2 000元.票价信息如下:
(1)请问参观历史博物馆和民俗展览馆的学生各有多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
解:(1)设参观历史博物馆的有x人,参观民俗展览馆的有y人.
依题意,得
解得
答:参观历史博物馆的有100人,参观民俗展览馆的有50人.
(2)2 000-150×10=500(元).
答:若学生都去参观历史博物馆,则能节省票款500元.
x+y=150,
10x+20y=2 000.
x=100,
y=50.
11. 一艘轮船在相距90 km的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6 h,逆流航行比顺流航行多用4 h.
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,则甲、丙两地相距多少千米?
解:(1)设该轮船在静水中的速度是x km/h,水流速度是y km/h.依题意,得
解得
答:该轮船在静水中的速度是12 km/h,水流速度是3 km/h.
6(x+y)=90,
(6+4)(x-y)=90.
x=12,
y=3.
(2)设甲、丙两地相距a km,则乙、丙两地相距(90-a)km.依题意,得
解得a=
答:甲、丙两地相距 km.
12. 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆.依题意,得
解得
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
36x+2=y,
22(x+4)-2=y.
x=6,
y=218.
(2)设需调配36座客车m辆,22座客车n辆.
依题意,得36m+22n=218.
所以n=
因为m,n均为正整数,所以
答:需调配36座客车3辆,22座客车5辆.
m=3,
n=5.
谢 谢
第五章 二元一次方程组
单元复习课
本章知识梳理
目录
01
课标要求
02
知识导航
课标要求
1.掌握代入消元法和加减消元法,能解二元一次方程组.
2.能根据具体问题的实际意义,检验方程的解是否合理.
3.体会一次函数与二元一次方程的关系.
知识导航
二元一次 方程组 基本概念 二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程.
二元一次方程的解:适合一个二元一次方程的一组未知数的值
二元一次方程组:共含有两个未知数的两个一次方程所组成的一组方程.
二元一次方程组的解:二元一次方程中各个方程的公共解
续表
二元一次 方程组 基本解法 代入消元法:将二元一次方程组其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程,从而消去一个未知数的解方程组的方法
加减消元法:将二元一次方程组的两个方程变形后,通过两式相加(减)消去其中一个未知数的解方程组的方法
续表
二元一次 方程组 实际应用 类型:鸡兔同笼、增收节支、里程碑上的数
二元一次方程(组)与一次函数的关系 1.方程的解与函数图象上的点的坐标一一对应;
2.两条直线的交点坐标就是相应的二元一次方程组的解,反之亦然
续表
二元一次 方程组 三元一次 方程组 三元一次方程:含有三个未知数,并且所含未知数的项的次数都是1的方程
三元一次方程组:共含有三个未知数的三个一次方程所组成的一组方程
三元一次方程组的解:三元一次方程中各个方程的公共解
三元一次方程组的解法:代入消元法、加减消元法
专题1 求解二元一次方程组
1.已知方程组 则x-y的值为( )
A. B.2 C.3 D.-2
2x+y=4,
x+2y=1
C
2. (2020牡丹江)若 是二元一次方程组
的解,则x+2y的算术平方根为( )
A. 3 B. ±3 C. D.±
a=2
b=1
ax+by=5
ax-by=2
C
3.若|3x-2y-1|+ =0,则x,y的值为( )
A.
x=1,
y=4
B.
x=2,
y=0
C.
x=0,
y=2
D.
x=1,
y=1
D
4. (2020南京)已知x,y满足方程组 则x+y的值为
_________.
x+3y=-1,
2x+y=3,
1
5. 解方程组:
x+y=1,
4x+y=10.
解:
②-①,得3x=9.
解得x=3.
把x=3代入①,得y=-2.
则原方程组的解为
x+y=1,①
4x+y=10.②
x=3,
y=-2.
6. 解方程组:
x+2y=0,
3x+4y=6.
解:
①×2-②,得-x=-6.
解得x=6.
将x=6代入①,得6+2y=0.
解得y=-3.
故原方程组的解为
x+2y=0,①
3x+4y=6.②
x=6,
y=-3.
7. (2020佛山)解方程组:
=2,
3(2x+1)-2(4y-3)=5.
解:设 =m, =n,将原方程组化为
①×4+②,得13m=13.解得m=1.
把m=1代入①,得n=1,即 =1, =1.
解得x=1,y=
所以原方程组的解为
m+n=2,①,
9m-4n=5.②
x=1,
y=
8. (2020陕西)已知方程组 和方程组
的解相同,试判断点P(a,b)在第几象限.
2x+y=-2,
ax-by=-4
3x-y=12,
bx+ay=-8
解:由2x+y=-2和3x-y=12组成方程组,解得
代入 得
解得
所以点P(1,-1)在第四象限.
x=2,
y=-6,
ax-by=-4,
bx+ay=-8,
2a+6b=-4,
2b-6a=-8,
a=1,
b=-1.
9. 已知两个方程组 和 有公共解,求a,b的值.
2x+y=5,
ax-by=-4
5x-4y=6,
2ax+3by=2
代入第二组方程组,得
解得
2a-b=-4,
4a+3b=2.
a=-1,
b=2.
解:因为方程组 和 有公共解,
所以原方程组可化为 和
由第一组方程组解得
2x+y=5,
ax-by=-4
5x-4y=6,
2ax+3by=2
2x+y=5,
5x-4y=6
ax-by=-4,
2ax+3by=2.
x=2,
y=1.
1.某出租车起步价所包含的路程为0~2 km,超过2 km的部分按每千米另收费.津津乘坐这种出租车行了7 km,付了16元;盼盼乘坐这种出租车行了13 km,付了28元.设这种出租车的起步价为x元,超过2 km后每千米收费y元,则下面所列方程组正确的是( )
专题2 应用二元一次方程组
D
A.
x+7y=16,
x+13y=28
B.
x+(7-2)y=16,
x+13y=28
C.
x+7y=16,
x+(13-2)y=28
D.
x+(7-2)y=16,
x+(13-2)y=28
2. (2020龙东)学校计划用200元钱购买A,B两种奖品,A种每个15元,B种每个25元,在钱全部用完的情况下,有多少种购买方案?( )
A. 2种 B. 3种
C. 4种 D.5种
B
3. 如图Z5-1所示的两台天平保持平衡,已知每块巧克力的重量相等,每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )
A.10 g,40 g B.15 g,35 g
C.20 g,30 g D.30 g,20 g
C
4. 如图Z5-2,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A.35
B.45
C.55
D.65
B
5. (2020常德)今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是_________次.
4
6.某活动小组购买了4个篮球和5个足球,一共花费了466元,其中篮球的单价比足球的单价多4元,求篮球和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意可列方程组为
__________________.
x-y=4,
4x+5y=466
7. 用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品.要生产甲种产品37件,乙种产品18件,则恰好需用A,B两种型号的钢板共_________块.
11
8. 某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年元旦期间的销售情况,下面是调查后小明与其他两位同学进行交流的情景.
小明说:“去年两家超市的销售额共为150万元,今年两家超市的销售额共为170万元.”
小亮说:“甲超市今年的销售额比去年增加10%.”
小颖说:“乙超市今年的销售额比去年增加20%.”
根据他们的对话,得出今年甲超市的销售额为_________万元.
110
9. (2020合肥)如图Z5-3所示是正方体的表面展开图,若正方体相对的两个面上的数或式子的值相等,求x和y的值.
解:由题意可列方程组为
解得
x-3=2y,
2x-1=y+2.
x=1,
y=-1.
地点 售价
历史博物馆 10元/人
民俗展览馆 20元/人
10. 本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆.每一名学生只能参加其中一项活动,共支付票款2 000元.票价信息如下:
(1)请问参观历史博物馆和民俗展览馆的学生各有多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
解:(1)设参观历史博物馆的有x人,参观民俗展览馆的有y人.
依题意,得
解得
答:参观历史博物馆的有100人,参观民俗展览馆的有50人.
(2)2 000-150×10=500(元).
答:若学生都去参观历史博物馆,则能节省票款500元.
x+y=150,
10x+20y=2 000.
x=100,
y=50.
11. 一艘轮船在相距90 km的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6 h,逆流航行比顺流航行多用4 h.
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,则甲、丙两地相距多少千米?
解:(1)设该轮船在静水中的速度是x km/h,水流速度是y km/h.依题意,得
解得
答:该轮船在静水中的速度是12 km/h,水流速度是3 km/h.
6(x+y)=90,
(6+4)(x-y)=90.
x=12,
y=3.
(2)设甲、丙两地相距a km,则乙、丙两地相距(90-a)km.依题意,得
解得a=
答:甲、丙两地相距 km.
12. 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆.依题意,得
解得
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
36x+2=y,
22(x+4)-2=y.
x=6,
y=218.
(2)设需调配36座客车m辆,22座客车n辆.
依题意,得36m+22n=218.
所以n=
因为m,n均为正整数,所以
答:需调配36座客车3辆,22座客车5辆.
m=3,
n=5.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
