人教版八年级上册 14.1.4 多项式乘多项式 (第3课时)课件(共14张PPT)
文档属性
| 名称 | 人教版八年级上册 14.1.4 多项式乘多项式 (第3课时)课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 638.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 09:46:50 | ||
图片预览





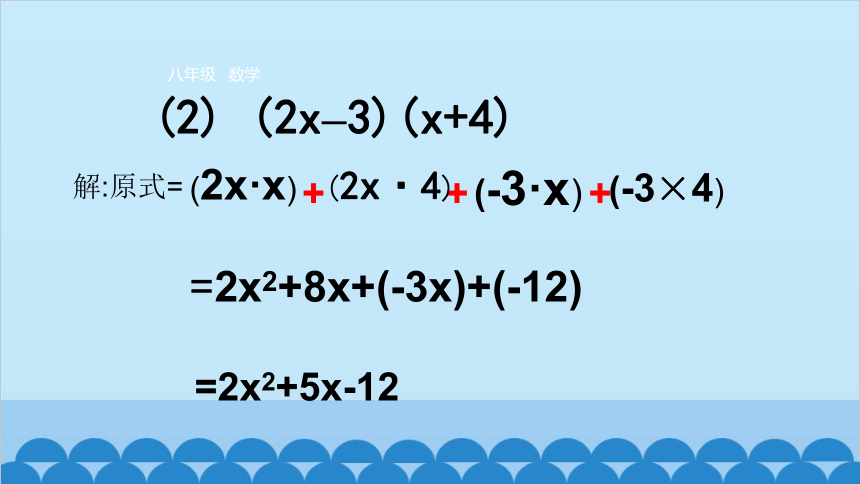
文档简介
(共14张PPT)
复 习 巩 固
1、 -x3y2(x+3y)
解 原式=-x4y2-3x3y3
解 原式=-2x2y3+6xy4
2、-2xy3(x-3y)
14.1.4 整式乘法(第3课时)
——多项式乘多项式
自学课本100-101页,思考:
1.问题3推导法则的过程你看懂了吗?
2.多项式乘多项式的法则是什么?用字母如何表示?
3.例6你看懂了吗?解题时符号怎么处理?格式怎样?你有不理解的地方吗?
多项式乘以多项式的乘法法则
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
感 受 新 知
+ + +
计算:
(1) (x+2y)(3a+2b)
解:原式=
(x·3a)
(x·2b)
(2y·2b)
(2y·3a)
=3ax+2bx+6ay+4by
八年级 数学
+ + +
(2) (2x–3)(x+4)
解:原式=
(2x·x)
(2x·4)
(-3·x)
(-3×4)
=2x2+8x+(-3x)+(-12)
=2x2+5x-12
(3) (-2x+3y)(x2-xy+2y2)
解:原式=
-2x·x2
+(-2x )·(-xy)
+(-2x)·2y2
+3y·x2
+3y·(-xy)
+3y·2y2
=-2x3 +2x2y-4xy2+3x2y-3xy2+6y3
=-2x3 +5x2y-7xy2+6y3
(1)(x+2y)(5a+3b)
(2) (2x–3)(x+4)
计算:
(3)(2a+b)2
(4)(x+y)(x2 –xy+y2 )
当堂训练
完成课本102页练习1、2(8分钟)
x
p+q
pq
根据上述求解过程,观察计算结果的各项系数与原式中的系数有怎样的关系?
根据上述结论计算:
(1) (x+1)(x+2)=
(2) (x+1)(x-2)=
(3) (x-1)(x+2)=
(4) (x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
(x+p)(x+q) = x2 + (p+q) x + p q
拓展与应用
当堂小结
1、你有什么收获?
2、你有什么疑惑?
当堂检测
练习 计算:
(1)
(2)
(3)
(4)
(5)
(6)
复 习 巩 固
1、 -x3y2(x+3y)
解 原式=-x4y2-3x3y3
解 原式=-2x2y3+6xy4
2、-2xy3(x-3y)
14.1.4 整式乘法(第3课时)
——多项式乘多项式
自学课本100-101页,思考:
1.问题3推导法则的过程你看懂了吗?
2.多项式乘多项式的法则是什么?用字母如何表示?
3.例6你看懂了吗?解题时符号怎么处理?格式怎样?你有不理解的地方吗?
多项式乘以多项式的乘法法则
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
感 受 新 知
+ + +
计算:
(1) (x+2y)(3a+2b)
解:原式=
(x·3a)
(x·2b)
(2y·2b)
(2y·3a)
=3ax+2bx+6ay+4by
八年级 数学
+ + +
(2) (2x–3)(x+4)
解:原式=
(2x·x)
(2x·4)
(-3·x)
(-3×4)
=2x2+8x+(-3x)+(-12)
=2x2+5x-12
(3) (-2x+3y)(x2-xy+2y2)
解:原式=
-2x·x2
+(-2x )·(-xy)
+(-2x)·2y2
+3y·x2
+3y·(-xy)
+3y·2y2
=-2x3 +2x2y-4xy2+3x2y-3xy2+6y3
=-2x3 +5x2y-7xy2+6y3
(1)(x+2y)(5a+3b)
(2) (2x–3)(x+4)
计算:
(3)(2a+b)2
(4)(x+y)(x2 –xy+y2 )
当堂训练
完成课本102页练习1、2(8分钟)
x
p+q
pq
根据上述求解过程,观察计算结果的各项系数与原式中的系数有怎样的关系?
根据上述结论计算:
(1) (x+1)(x+2)=
(2) (x+1)(x-2)=
(3) (x-1)(x+2)=
(4) (x-1)(x-2)=
x2+3x+2
x2-x-2
x2+x-2
x2-3x+2
(x+p)(x+q) = x2 + (p+q) x + p q
拓展与应用
当堂小结
1、你有什么收获?
2、你有什么疑惑?
当堂检测
练习 计算:
(1)
(2)
(3)
(4)
(5)
(6)
