人教版八年级上册 12.3 角平分线的性质(第1课时) 课件(共17张PPT)
文档属性
| 名称 | 人教版八年级上册 12.3 角平分线的性质(第1课时) 课件(共17张PPT) | 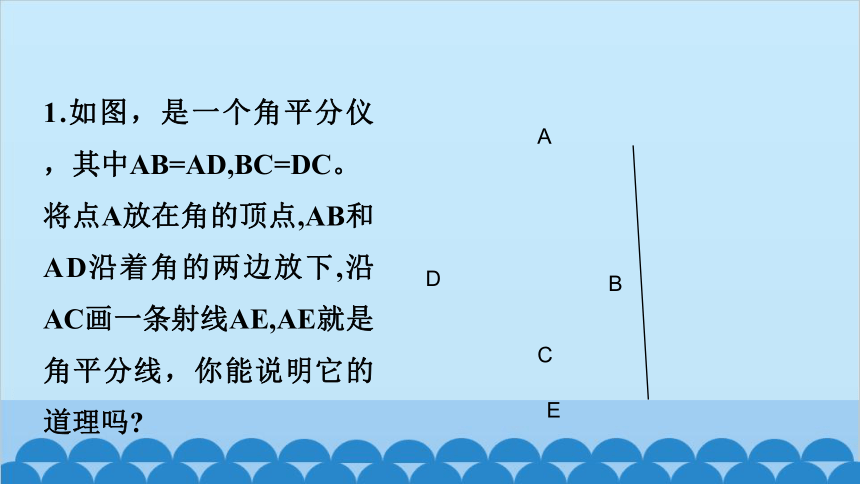 | |
| 格式 | ppt | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 09:49:30 | ||
图片预览



文档简介
(共18张PPT)
1.如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
D
B
C
E
12.3角平分线的性质(1)
A
D
B
C
E
如图是一个角平分仪,其中AB=AD,BC=DC。
你能说明它的道理吗
1.证明:在△ACD和△ACB中
∴ △ACD≌ △ACB(SSS)
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∵
∴∠CAD=∠CAB(全等三角形的对应边相等)
∴AC平分∠DAB(角平分线的定义)
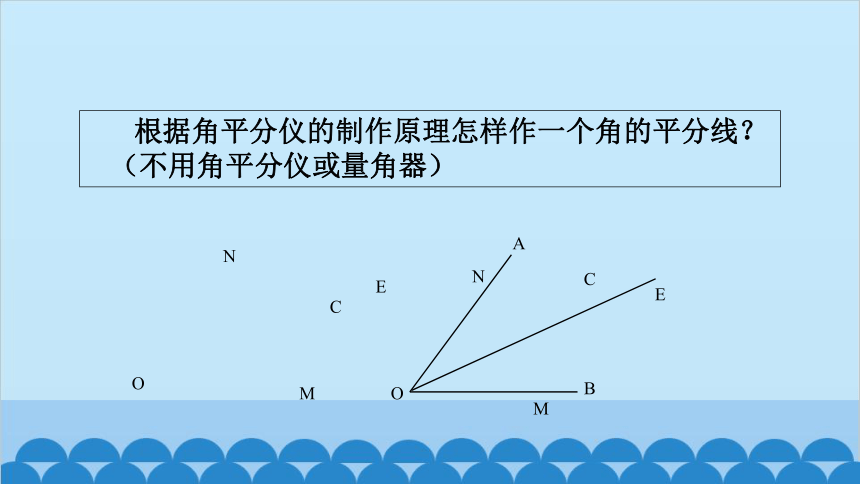
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
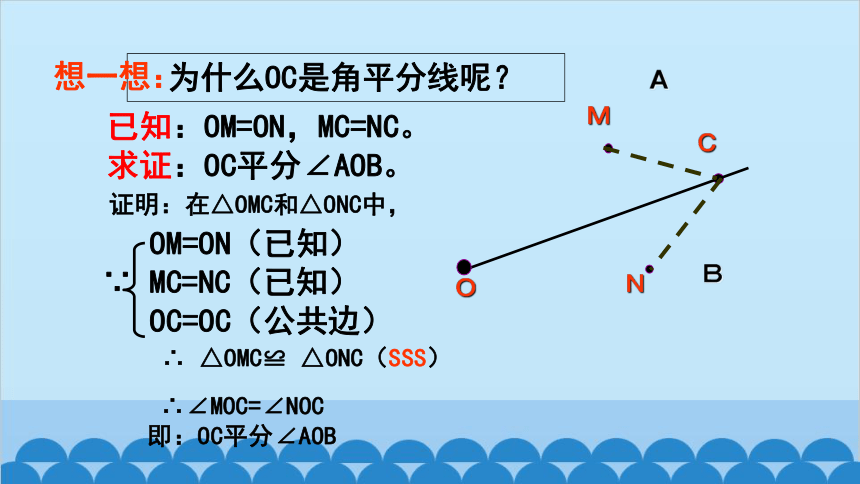
为什么OC是角平分线呢?
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
A
B
M
N
C
O
OM=ON(已知)
∵ MC=NC(已知)
OC=OC(公共边)
证明:在△OMC和△ONC中,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
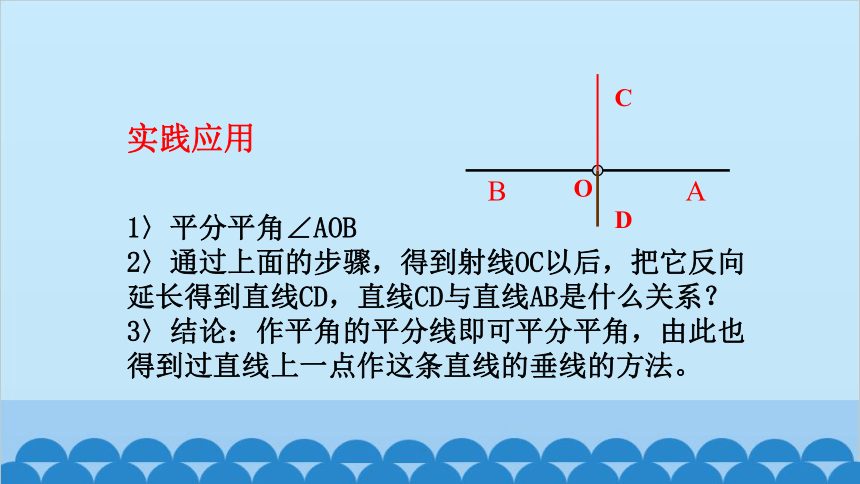
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
实践应用
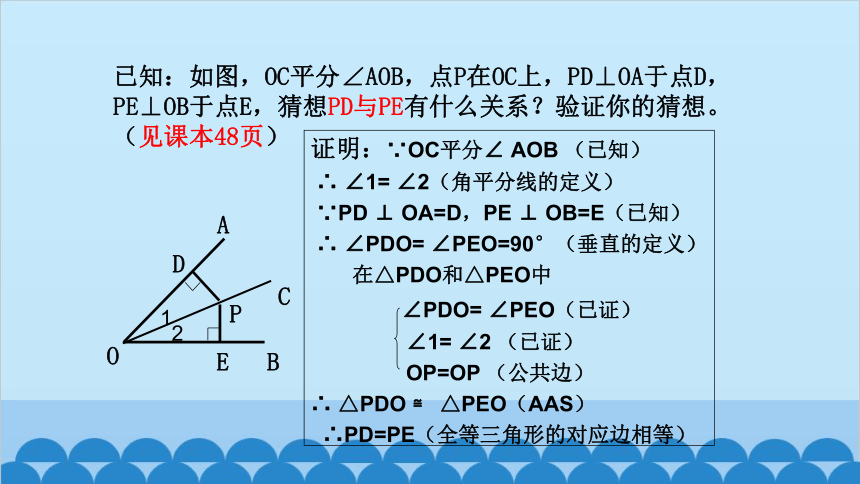
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA=D,PE ⊥ OB=E(已知)
∴ ∠PDO= ∠PEO=90°(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,猜想PD与PE有什么关系?验证你的猜想。(见课本48页)
角平分线的性质
定理:角的平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵∠1=∠2
(或OP平分∠AOB)
PD⊥OA=D,PE⊥OB=E
∴PD=PE(角的平分线上的点到角的两边的距离相等)
作用:证明线段相等。
∵ 如图,AD平分∠BAC(已知)
∴ = ,
BD CD
(×)
1.判断
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,
DB
DC
(√)
不必再证三角形全等!
2、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
3、在△OAB中,OE是它的角平分线,且EA=EB,EC、ED分别垂直OA,OB,垂足为C,D. 求证:AC=BD.
O
A
B
E
C
D
课堂小结
角的平分线上的点到角的两边的距离相等.
本节课我们学习了角平分线性质(学生口答)——
1.已知△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
当堂检测
2、 在△ABC中, ∠ C=90 ° ,AD是∠BAC的平分线,DE⊥AB于E,BC=7,DE=3.求BD的长。
E
D
C
B
A
备选练习: 如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF 求证:CF=EB
A
C
D
E
B
F
1.如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗
A
D
B
C
E
12.3角平分线的性质(1)
A
D
B
C
E
如图是一个角平分仪,其中AB=AD,BC=DC。
你能说明它的道理吗
1.证明:在△ACD和△ACB中
∴ △ACD≌ △ACB(SSS)
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∵
∴∠CAD=∠CAB(全等三角形的对应边相等)
∴AC平分∠DAB(角平分线的定义)
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
为什么OC是角平分线呢?
想一想:
已知:OM=ON,MC=NC。
求证:OC平分∠AOB。
A
B
M
N
C
O
OM=ON(已知)
∵ MC=NC(已知)
OC=OC(公共边)
证明:在△OMC和△ONC中,
∴ △OMC≌ △ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
实践应用
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA=D,PE ⊥ OB=E(已知)
∴ ∠PDO= ∠PEO=90°(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,猜想PD与PE有什么关系?验证你的猜想。(见课本48页)
角平分线的性质
定理:角的平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵∠1=∠2
(或OP平分∠AOB)
PD⊥OA=D,PE⊥OB=E
∴PD=PE(角的平分线上的点到角的两边的距离相等)
作用:证明线段相等。
∵ 如图,AD平分∠BAC(已知)
∴ = ,
BD CD
(×)
1.判断
∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,
BD CD
(×)
∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = ,
DB
DC
(√)
不必再证三角形全等!
2、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
3、在△OAB中,OE是它的角平分线,且EA=EB,EC、ED分别垂直OA,OB,垂足为C,D. 求证:AC=BD.
O
A
B
E
C
D
课堂小结
角的平分线上的点到角的两边的距离相等.
本节课我们学习了角平分线性质(学生口答)——
1.已知△ABC中, ∠C=900,AD平分∠ CAB,且
BC=8,BD=5,求点D到AB的距离是多少?
A
B
C
D
E
当堂检测
2、 在△ABC中, ∠ C=90 ° ,AD是∠BAC的平分线,DE⊥AB于E,BC=7,DE=3.求BD的长。
E
D
C
B
A
备选练习: 如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF 求证:CF=EB
A
C
D
E
B
F
