人教版七年级上册 1.2.4 绝对值( 第1课时) 课件(共24张PPT)
文档属性
| 名称 | 人教版七年级上册 1.2.4 绝对值( 第1课时) 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 09:57:26 | ||
图片预览








文档简介
(共24张PPT)
1.2.4 绝对值
教学目标:
1.知识与技能
①能根据一个数的绝对值表示“距离”,初步理解绝对值的概念,能求一个数的绝对值.
②通过应用绝对值解决实际问题,体会绝对值的意义和作用.
2.过程与方法
经历绝对值的代数定义转化成数学式子的过程中,培养学生运用数学转化思想指导思维活动的能力.
3.情感、态度与价值观
①通过解释绝对值的几何意义,渗透数形结合的思想.
②体验运用直观知识解决数学问题的成功.
教学重点:
绝对值概念的形成过程,运用定义求绝对值
教学难点:
绝对值的概念的理解.
学习目标:
①能根据一个数的绝对值表示“距离”,初步理解绝对值的概念,能求一个数的绝对值.
②通过应用绝对值解决实际问题,体会绝对值的意义和作用.
观察 出示一组数6与-6,3.5与-3.5,1和-1,它们是一对互为________,它们的__________不同,__________相同.
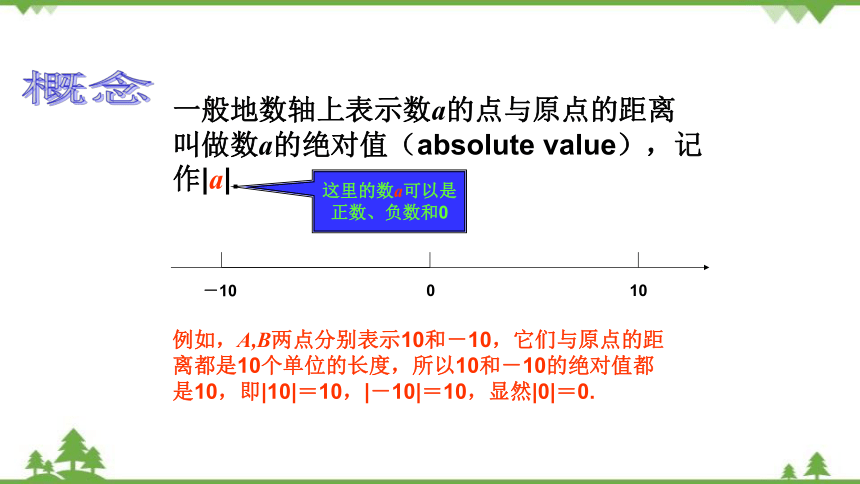
一般地数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value),记作|a|.
例如,A,B两点分别表示10和-10,它们与原点的距离都是10个单位的长度,所以10和-10的绝对值都是10,即|10|=10,|-10|=10,显然|0|=0.
这里的数a可以是正数、负数和0
0
10
-10
想一想
(1)-3的绝对值是什么?
(2)+2 的绝对值是多少?
(3)-12的绝对值呢?
(4)a的绝对值呢?
讨论交流
正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是零.
总结 正数的绝对值是它本身.
负数的绝对值是它的相反数.
零的绝对值是零.
例题填空:
(1)绝对值等于4的数有 2 个,它们是 ±4 .
(2)绝对值等于-3的数有 0 个.
(3)绝对值等于本身的数有 无数 个,它们是 0和正数(非负数) .
(4)①若│a│=2,则a= ±2 .
②若│-a│=3,则a= ±3 .
(5)绝对值不大于2的整数是 0,±1,±2 .
(6)根据绝对值的意义,思考:
①如果=1,那么a > 0;
②如果=-1,那么a < 0;
③如果a<0,那么-│a│= a .
任何一个有理数的绝对值都是非负数.
6, -8, -0.9 100, 0
写出下列各数的绝对值
|6|=6
|-8|=8
|-0.9|=0.9
|100|=100
|0|=0
解:
判断下列说法是否正确
例6 已知有理数a、b、c在数轴上的位置如图,化简
.
思考:
0
0
0
0
任何一个有理数的绝对值都是非负数.
考考你!!
1,如果 ,
则 a=_____,b=_____.
2,己知X=30,Y=-4,
则
2、一个数的绝对值是7,求这个数?
3、满足︱x︱≤3的所有整数是 ;
4、绝对值大于2并且不大于5的整数有 。
1、判断下列说法是否正确:
(1)有理数的绝对值一定是正数;
(2)如果两个数的绝对值相等,那么这两个数相等;
(3)符号相反且绝对值相等的数互为相反数;
(4)一个数的绝对值越大,表示它的点在数轴上越靠右;
(5)一个数的绝对值越大,表示它的点在数轴上离原点越远。
2、猜一猜,我是谁?
(1)绝对值是它本身的数是 ;
(2)绝对值是它的相反数的是 。
3、设a是最小的自然数,b是绝对值最小的数 ,c是相反数等于它本身的数,则a+b+c= .
正数、0
负数、0
a=0,b=0,c=0
0
1、一个有理数有几部分组成?
2、已知︱x︱=6, ︱y︱=4,并且x>y,求x+y的值;
3、根据绝对值的意义,思考:
(1)如果—=1,那么a 0;
(2)如果a<0,那么-︱a︱= 。
︱a︱
a
1你获得那些知识?
一般地数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value),记作|a|.
这里的数a可以是正数、负数和0
一个正数的绝对值是 它本身, 一个负数的绝对值是它的相反数 0的绝对值是0
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当a是0时,|a|=0
1.2.4 绝对值
教学目标:
1.知识与技能
①能根据一个数的绝对值表示“距离”,初步理解绝对值的概念,能求一个数的绝对值.
②通过应用绝对值解决实际问题,体会绝对值的意义和作用.
2.过程与方法
经历绝对值的代数定义转化成数学式子的过程中,培养学生运用数学转化思想指导思维活动的能力.
3.情感、态度与价值观
①通过解释绝对值的几何意义,渗透数形结合的思想.
②体验运用直观知识解决数学问题的成功.
教学重点:
绝对值概念的形成过程,运用定义求绝对值
教学难点:
绝对值的概念的理解.
学习目标:
①能根据一个数的绝对值表示“距离”,初步理解绝对值的概念,能求一个数的绝对值.
②通过应用绝对值解决实际问题,体会绝对值的意义和作用.
观察 出示一组数6与-6,3.5与-3.5,1和-1,它们是一对互为________,它们的__________不同,__________相同.
一般地数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value),记作|a|.
例如,A,B两点分别表示10和-10,它们与原点的距离都是10个单位的长度,所以10和-10的绝对值都是10,即|10|=10,|-10|=10,显然|0|=0.
这里的数a可以是正数、负数和0
0
10
-10
想一想
(1)-3的绝对值是什么?
(2)+2 的绝对值是多少?
(3)-12的绝对值呢?
(4)a的绝对值呢?
讨论交流
正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是零.
总结 正数的绝对值是它本身.
负数的绝对值是它的相反数.
零的绝对值是零.
例题填空:
(1)绝对值等于4的数有 2 个,它们是 ±4 .
(2)绝对值等于-3的数有 0 个.
(3)绝对值等于本身的数有 无数 个,它们是 0和正数(非负数) .
(4)①若│a│=2,则a= ±2 .
②若│-a│=3,则a= ±3 .
(5)绝对值不大于2的整数是 0,±1,±2 .
(6)根据绝对值的意义,思考:
①如果=1,那么a > 0;
②如果=-1,那么a < 0;
③如果a<0,那么-│a│= a .
任何一个有理数的绝对值都是非负数.
6, -8, -0.9 100, 0
写出下列各数的绝对值
|6|=6
|-8|=8
|-0.9|=0.9
|100|=100
|0|=0
解:
判断下列说法是否正确
例6 已知有理数a、b、c在数轴上的位置如图,化简
.
思考:
0
0
0
0
任何一个有理数的绝对值都是非负数.
考考你!!
1,如果 ,
则 a=_____,b=_____.
2,己知X=30,Y=-4,
则
2、一个数的绝对值是7,求这个数?
3、满足︱x︱≤3的所有整数是 ;
4、绝对值大于2并且不大于5的整数有 。
1、判断下列说法是否正确:
(1)有理数的绝对值一定是正数;
(2)如果两个数的绝对值相等,那么这两个数相等;
(3)符号相反且绝对值相等的数互为相反数;
(4)一个数的绝对值越大,表示它的点在数轴上越靠右;
(5)一个数的绝对值越大,表示它的点在数轴上离原点越远。
2、猜一猜,我是谁?
(1)绝对值是它本身的数是 ;
(2)绝对值是它的相反数的是 。
3、设a是最小的自然数,b是绝对值最小的数 ,c是相反数等于它本身的数,则a+b+c= .
正数、0
负数、0
a=0,b=0,c=0
0
1、一个有理数有几部分组成?
2、已知︱x︱=6, ︱y︱=4,并且x>y,求x+y的值;
3、根据绝对值的意义,思考:
(1)如果—=1,那么a 0;
(2)如果a<0,那么-︱a︱= 。
︱a︱
a
1你获得那些知识?
一般地数轴上表示数a的点与原点的距离叫做数a的绝对值(absolute value),记作|a|.
这里的数a可以是正数、负数和0
一个正数的绝对值是 它本身, 一个负数的绝对值是它的相反数 0的绝对值是0
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当a是0时,|a|=0
