数学人教A版2019必修第一册3.2.1函数的基本性质-单调性 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版2019必修第一册3.2.1函数的基本性质-单调性 课件(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 13:06:33 | ||
图片预览






文档简介
(共24张PPT)
3.2.1 函数的单调性
函数的概念与性质
课程标准
借助函数图像,会用符号语言表达函数单调性(会用定义法证明函数单调性),理解他们的作用与实际意义
复习回顾
问题1 函数的概念是什么?它的表示方法有哪些?
新课导入
我们知道函数描述了客观世界中变量之间的一种对应关系.这样我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律.
因此,研究函数的性质,如随着自变量的增大函数值是增大还是减小,有没有最大值或最小值,函数图象有什么特征等,是认识客观规律的重要方法.
新课导入
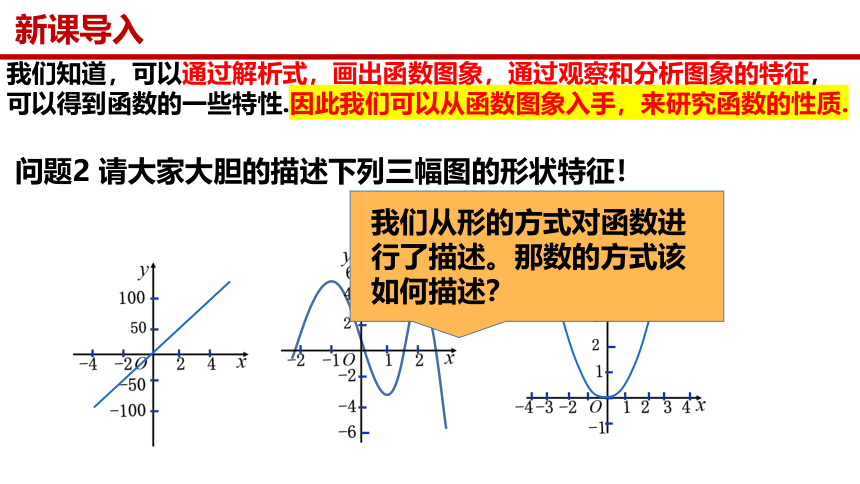
我们知道,可以通过解析式,画出函数图象,通过观察和分析图象的特征,可以得到函数的一些特性.因此我们可以从函数图象入手,来研究函数的性质.
问题2 请大家大胆的描述下列三幅图的形状特征!
我们从形的方式对函数进行了描述。那数的方式该如何描述?
一
二
三
教学目标
用从函数图像求函数的单调,直观感知函数的单调性
会用数学语言描述函数的单调性
会用定义法证明函数单调性
教学目标
难点
重点
易错点
新知探究
探究一:通过函数解析式画出函数图像,用数学语言描述函数单调性
新知讲解
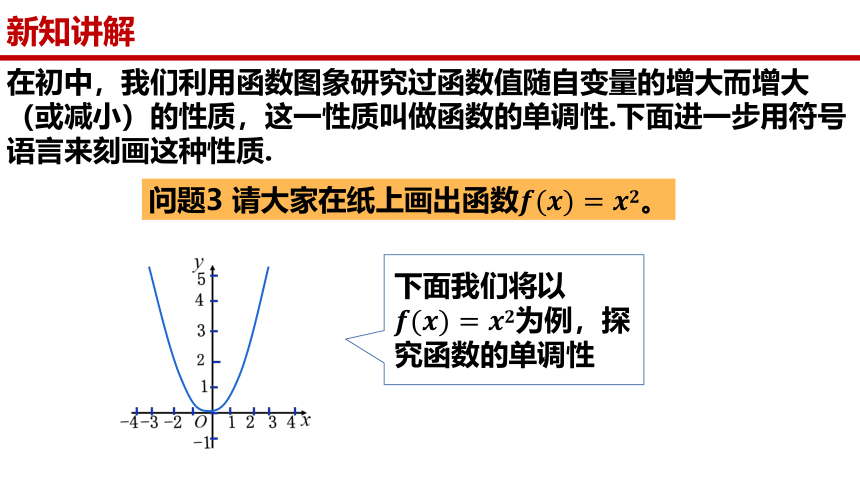
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫做函数的单调性.下面进一步用符号语言来刻画这种性质.
问题3 请大家在纸上画出函数。
下面我们将以为例,探究函数的单调性
新知探究
追问1 在中你能发现它的单调性是怎样的?
在轴左侧,图象下降的;
即当时,即随着的增大而减小;
在轴右侧,图象上升的;
即当时,即随着的增大而增大.
新知探究
追问2 那我们该如何用数学语言描述呢?
在轴左侧,图象下降的;
即当时,即随着的增大而减小;
这时我们就说函数在区间上是单调递减的.
符号语言
任意取,
当有
思考:
(1)你能说明为什么吗?
(2)如果,且单调递减,你们得到什么结论?
新知探究
在轴右侧,图象上升的;
即当时,即随着的增大而增大.
符号语言:任意取,
当,有
这时我们就说函数在区间上是单调递增的.
思考:
(1)你能说明为什么吗?
(2)如果,且单调递增,你们得到什么结论?
问题4 仿照,用符号语言刻画函数和各有怎样的单调性?
要求:(1)画出函数图像
(2)用数学语言描述函数单调性
合作探究
新知讲解
5
符号语言:
(1)任意取,
当
函数在区间上是单调递增的.
(2)任意取,
当
函数在区间上是单调递减的.
新知讲解
符号语言:
(1)任意取,
函数在区间上是单调递减的.
(2)任意取,
函数在区间上是单调递增的.
概念生成
一般地,设函数:
如果,当时,都有,那么就称函数在区间上单调递增.
就叫做函数的单调递增区间,简称增区间.
如果,当时,都有,那么就称函数在区间上单调递减.
就叫做函数的单调递增区间,简称减区间.
特别地,当函数在它的定义域上单调递减增时,我们就称它为增函数.
如:就是在R上的增函数.
特别地,当函数在它的定义域上单调递减减时,我们就称它为减函数.
如:就是在R上的减函数.
课堂练习
问题5 反比例函数是减函数吗?
我们该怎么描述它的单调性?
1.先画图
·
·
注意:增函数、减函数是针对的是函数的整个定义域,是函数的整体性质,而函数的单调性是对定义域下的某个区间,是函数的局部性质。一个函数在定义域下的某个区间具有单调性,但在整个定义上不一定具有单调性。
分段描述!
新知讲解
问题6 设A是区间D上的自变量的某些值组成的集合,而且,当x1对于函数,取区间,
集合,则,当,都有.但在上并不单调递增.
5
新知探究
探究二:用定义法证明函数单调性
新知讲解
例1 根据定义,研究函数的单调性。
追问1 回忆下初中所学的知识,影响函数单调性的字母是哪个?
它是如何影响的?请你以分类谈论的方式描述函数的单调性。
追问2 根据单调性的定义,判断单调性的关键是什么?
是比较的大小?
追问3 那如何比较的大小呢?
例题讲解
问题7 根据定义,研究函数的单调性。
比较的大小!
定义法判断函数单调性的四个步骤:
(1)取值;
(2)作差;
(3)定号;
(4)下结论.
例题讲解
例2 物理学中的玻意尔定律(为正常数)告诉我们,对于一定量的气体,当其体积减少时,压强将增大。试对此函数的点调性进行证明。
追问1 “体积减少时,压强增大”的数学意义是什么?
证明:
例3:根据定义证明函数在区间上单调递增.
证明:
(
所以,
又由,得
于是
所以,函数在区间上单调递增.
例题讲解
例题讲解
变式证明函数在区间上是减函数.
证明:
(
所以,
又由,得
于是
所以,函数在区间上单调递增.
的图像双勾图!
小结
(1)增函数、减函数的定义.
(2)用定义法证明函数的单调性.
(1)取值;
(2)作差;
(3)定号;
(4)下结论.
数形结合
3.2.1 函数的单调性
函数的概念与性质
课程标准
借助函数图像,会用符号语言表达函数单调性(会用定义法证明函数单调性),理解他们的作用与实际意义
复习回顾
问题1 函数的概念是什么?它的表示方法有哪些?
新课导入
我们知道函数描述了客观世界中变量之间的一种对应关系.这样我们就可以通过研究函数的变化规律来把握客观世界中事物的变化规律.
因此,研究函数的性质,如随着自变量的增大函数值是增大还是减小,有没有最大值或最小值,函数图象有什么特征等,是认识客观规律的重要方法.
新课导入
我们知道,可以通过解析式,画出函数图象,通过观察和分析图象的特征,可以得到函数的一些特性.因此我们可以从函数图象入手,来研究函数的性质.
问题2 请大家大胆的描述下列三幅图的形状特征!
我们从形的方式对函数进行了描述。那数的方式该如何描述?
一
二
三
教学目标
用从函数图像求函数的单调,直观感知函数的单调性
会用数学语言描述函数的单调性
会用定义法证明函数单调性
教学目标
难点
重点
易错点
新知探究
探究一:通过函数解析式画出函数图像,用数学语言描述函数单调性
新知讲解
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫做函数的单调性.下面进一步用符号语言来刻画这种性质.
问题3 请大家在纸上画出函数。
下面我们将以为例,探究函数的单调性
新知探究
追问1 在中你能发现它的单调性是怎样的?
在轴左侧,图象下降的;
即当时,即随着的增大而减小;
在轴右侧,图象上升的;
即当时,即随着的增大而增大.
新知探究
追问2 那我们该如何用数学语言描述呢?
在轴左侧,图象下降的;
即当时,即随着的增大而减小;
这时我们就说函数在区间上是单调递减的.
符号语言
任意取,
当有
思考:
(1)你能说明为什么吗?
(2)如果,且单调递减,你们得到什么结论?
新知探究
在轴右侧,图象上升的;
即当时,即随着的增大而增大.
符号语言:任意取,
当,有
这时我们就说函数在区间上是单调递增的.
思考:
(1)你能说明为什么吗?
(2)如果,且单调递增,你们得到什么结论?
问题4 仿照,用符号语言刻画函数和各有怎样的单调性?
要求:(1)画出函数图像
(2)用数学语言描述函数单调性
合作探究
新知讲解
5
符号语言:
(1)任意取,
当
函数在区间上是单调递增的.
(2)任意取,
当
函数在区间上是单调递减的.
新知讲解
符号语言:
(1)任意取,
函数在区间上是单调递减的.
(2)任意取,
函数在区间上是单调递增的.
概念生成
一般地,设函数:
如果,当时,都有,那么就称函数在区间上单调递增.
就叫做函数的单调递增区间,简称增区间.
如果,当时,都有,那么就称函数在区间上单调递减.
就叫做函数的单调递增区间,简称减区间.
特别地,当函数在它的定义域上单调递减增时,我们就称它为增函数.
如:就是在R上的增函数.
特别地,当函数在它的定义域上单调递减减时,我们就称它为减函数.
如:就是在R上的减函数.
课堂练习
问题5 反比例函数是减函数吗?
我们该怎么描述它的单调性?
1.先画图
·
·
注意:增函数、减函数是针对的是函数的整个定义域,是函数的整体性质,而函数的单调性是对定义域下的某个区间,是函数的局部性质。一个函数在定义域下的某个区间具有单调性,但在整个定义上不一定具有单调性。
分段描述!
新知讲解
问题6 设A是区间D上的自变量的某些值组成的集合,而且,当x1
集合,则,当,都有.但在上并不单调递增.
5
新知探究
探究二:用定义法证明函数单调性
新知讲解
例1 根据定义,研究函数的单调性。
追问1 回忆下初中所学的知识,影响函数单调性的字母是哪个?
它是如何影响的?请你以分类谈论的方式描述函数的单调性。
追问2 根据单调性的定义,判断单调性的关键是什么?
是比较的大小?
追问3 那如何比较的大小呢?
例题讲解
问题7 根据定义,研究函数的单调性。
比较的大小!
定义法判断函数单调性的四个步骤:
(1)取值;
(2)作差;
(3)定号;
(4)下结论.
例题讲解
例2 物理学中的玻意尔定律(为正常数)告诉我们,对于一定量的气体,当其体积减少时,压强将增大。试对此函数的点调性进行证明。
追问1 “体积减少时,压强增大”的数学意义是什么?
证明:
例3:根据定义证明函数在区间上单调递增.
证明:
(
所以,
又由,得
于是
所以,函数在区间上单调递增.
例题讲解
例题讲解
变式证明函数在区间上是减函数.
证明:
(
所以,
又由,得
于是
所以,函数在区间上单调递增.
的图像双勾图!
小结
(1)增函数、减函数的定义.
(2)用定义法证明函数的单调性.
(1)取值;
(2)作差;
(3)定号;
(4)下结论.
数形结合
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
