数学人教A版(2019)选择性必修第一册2.2.1 直线的点斜式方程 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.1 直线的点斜式方程 课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 642.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第二章 直线与圆的方程
2.2.1 直线的点斜式方程
学习目标
1. 了解用斜率公式推导点斜式方程的过程.
2. 掌握直线的点斜式方程与斜截式方程.
3.会利用直线的点斜式解决有关的问题.
一 新课引入
直线的斜率从数的角度刻画了直线相当于x轴的倾斜程度,并导出了用直线上的已知两点坐标来计算这它的公式.但它还不是直线上的点满足规律的一般表达.
我们需要建立直线上任意点(x,y)中的x与y之间一般表达式。
怎么建立呢?
二 讲授新课
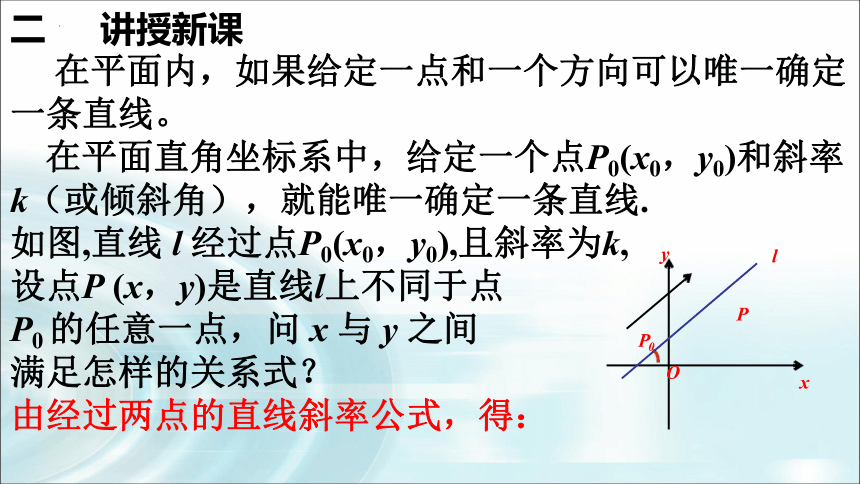
在平面内,如果给定一点和一个方向可以唯一确定一条直线。
在平面直角坐标系中,给定一个点P0(x0,y0)和斜率k(或倾斜角),就能唯一确定一条直线.
如图,直线 l 经过点P0(x0,y0),且斜率为k,
设点P (x,y)是直线l上不同于点
P0 的任意一点,问 x 与 y 之间
满足怎样的关系式?
由经过两点的直线斜率公式,得:
P0
P
l
x
y
O
如x1≠x0,则k= 这说明过P1、P0的直线的斜率相等,并且都过点P0,故两直线重合。
则P1在直线l上
综上,直线l与其点斜式方程一一对应。
即是说:过点P0、斜率为k的的方程是
y-y0=k(x-x0)
直线的点斜式方程:
过点P0(x0,y0)且斜率为k直线方程是:
y-y0=k(x-x0)
方程由直线上一点及其斜率确定的方程,我们称它为直线的点斜式方程.简称点斜式.
注 当直线l的倾斜角为 90°时 ,l与x轴垂直,斜率 k 不存在,是不能使用点斜式的。
O
x
y
P0
x-x0=0,或x=x
直线上任意一点的横坐标都是x0
例1:一条直线经过点P0(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。
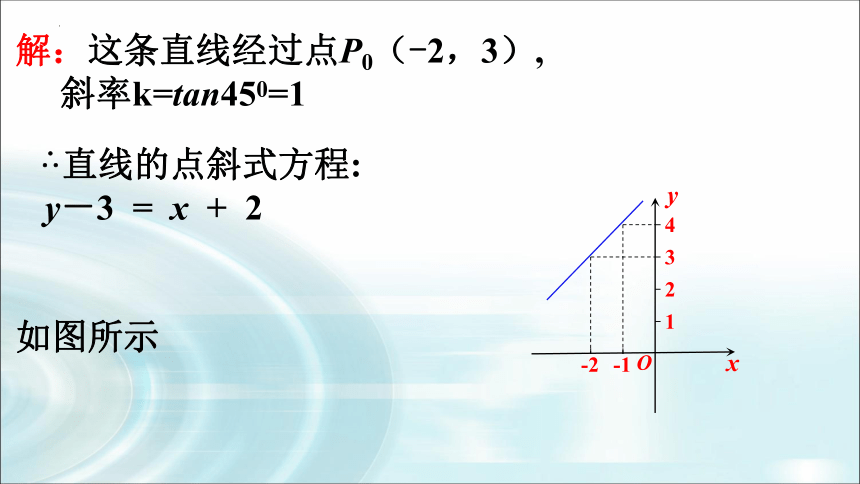
解:这条直线经过点P0(-2,3),
斜率k=tan450=1
∴直线的点斜式方程:
y-3 = x + 2
如图所示
y
1
2
3
4
x
O
-1
-2
跟踪练习:
写出下列直线的点斜式方程:
(1)经过A(3,-1),斜率是
(2)经过B(- ,2), 倾斜角是30°
(3)经过点P(5,-2),且与y轴平行;
(4)经过P(-2,3),Q(5,-4)两点.
分析
(1) 直接利用点斜式
y+1 = (x-3)
(2)y-2 = (x+ 1 )
(3)斜率不存在.
所求方程x=5
(4)先求斜率,k=-1,
再用点斜式得:
y-3 =- (x+2)
直线的斜截式方程
已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程.
O
x
y
(0,b)
y - b =k ( x - 0)
即 y = k x + b .
称直线方程的斜截式,
注 斜截式方程是点斜式方程的特例
定义 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距;直线l与x轴交点(a,0)的横坐标a叫做直线l在x轴上的截距.截距不是距离,是一个实数
例2. 已知直线l1 : y=k1x+b1,l2 : y=k2x+b2
试讨论:
(1)l1∥l2的条件是什么?
(2)l1 l2 的条件是什么?
分析:
(1)l1∥l2的条件是:方向相同,截距不同
即k1 =k2, 且b1 ≠ b2
(2)l1 l2 的条件是 k1 k2 =-1
跟踪练习:
根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;
(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3
分析:
(1)由直线方程的斜截式可知,
所求直线方程为y=2x+5.
(2)由于直线的倾斜角为150°,k=-
∴ y=-x-2
(3)k=,
由于直线与x轴的交点到原点的距离3,
所以截距b=3或b=-3
所求直线 y=x+3,或y=x-3
三 课堂小结
(1)直线的点斜式方程适用前提是:
直线的斜率存在并且已知,还要已知一个点;
(2)直线的斜截式方程y=kx+b是点斜式方程特例.
它的特点是:
要确定直线方程,只需知道参数k,b的值即可.
五 作业
课本 P64 练习 2,3
第二章 直线与圆的方程
2.2.1 直线的点斜式方程
学习目标
1. 了解用斜率公式推导点斜式方程的过程.
2. 掌握直线的点斜式方程与斜截式方程.
3.会利用直线的点斜式解决有关的问题.
一 新课引入
直线的斜率从数的角度刻画了直线相当于x轴的倾斜程度,并导出了用直线上的已知两点坐标来计算这它的公式.但它还不是直线上的点满足规律的一般表达.
我们需要建立直线上任意点(x,y)中的x与y之间一般表达式。
怎么建立呢?
二 讲授新课
在平面内,如果给定一点和一个方向可以唯一确定一条直线。
在平面直角坐标系中,给定一个点P0(x0,y0)和斜率k(或倾斜角),就能唯一确定一条直线.
如图,直线 l 经过点P0(x0,y0),且斜率为k,
设点P (x,y)是直线l上不同于点
P0 的任意一点,问 x 与 y 之间
满足怎样的关系式?
由经过两点的直线斜率公式,得:
P0
P
l
x
y
O
如x1≠x0,则k= 这说明过P1、P0的直线的斜率相等,并且都过点P0,故两直线重合。
则P1在直线l上
综上,直线l与其点斜式方程一一对应。
即是说:过点P0、斜率为k的的方程是
y-y0=k(x-x0)
直线的点斜式方程:
过点P0(x0,y0)且斜率为k直线方程是:
y-y0=k(x-x0)
方程由直线上一点及其斜率确定的方程,我们称它为直线的点斜式方程.简称点斜式.
注 当直线l的倾斜角为 90°时 ,l与x轴垂直,斜率 k 不存在,是不能使用点斜式的。
O
x
y
P0
x-x0=0,或x=x
直线上任意一点的横坐标都是x0
例1:一条直线经过点P0(-2,3),倾斜角α=450,求这条直线的方程,并画出图形。
解:这条直线经过点P0(-2,3),
斜率k=tan450=1
∴直线的点斜式方程:
y-3 = x + 2
如图所示
y
1
2
3
4
x
O
-1
-2
跟踪练习:
写出下列直线的点斜式方程:
(1)经过A(3,-1),斜率是
(2)经过B(- ,2), 倾斜角是30°
(3)经过点P(5,-2),且与y轴平行;
(4)经过P(-2,3),Q(5,-4)两点.
分析
(1) 直接利用点斜式
y+1 = (x-3)
(2)y-2 = (x+ 1 )
(3)斜率不存在.
所求方程x=5
(4)先求斜率,k=-1,
再用点斜式得:
y-3 =- (x+2)
直线的斜截式方程
已知直线l的斜率是k,与y轴的交点是P(0,b),求直线方程.
O
x
y
(0,b)
y - b =k ( x - 0)
即 y = k x + b .
称直线方程的斜截式,
注 斜截式方程是点斜式方程的特例
定义 直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距;直线l与x轴交点(a,0)的横坐标a叫做直线l在x轴上的截距.截距不是距离,是一个实数
例2. 已知直线l1 : y=k1x+b1,l2 : y=k2x+b2
试讨论:
(1)l1∥l2的条件是什么?
(2)l1 l2 的条件是什么?
分析:
(1)l1∥l2的条件是:方向相同,截距不同
即k1 =k2, 且b1 ≠ b2
(2)l1 l2 的条件是 k1 k2 =-1
跟踪练习:
根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为150°,在y轴上的截距是-2;
(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3
分析:
(1)由直线方程的斜截式可知,
所求直线方程为y=2x+5.
(2)由于直线的倾斜角为150°,k=-
∴ y=-x-2
(3)k=,
由于直线与x轴的交点到原点的距离3,
所以截距b=3或b=-3
所求直线 y=x+3,或y=x-3
三 课堂小结
(1)直线的点斜式方程适用前提是:
直线的斜率存在并且已知,还要已知一个点;
(2)直线的斜截式方程y=kx+b是点斜式方程特例.
它的特点是:
要确定直线方程,只需知道参数k,b的值即可.
五 作业
课本 P64 练习 2,3
