11.2.2 三角形的外角 课件(共25张PPT)
文档属性
| 名称 | 11.2.2 三角形的外角 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 15:26:35 | ||
图片预览




文档简介
(共25张PPT)
11.2.2 三角形的外角
人教版八年级上册
知识回顾
1.三角形内角和定理:
2.直角三角形性质:
3.直角三角形判定:
三角形三个内角的和等于180°.
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
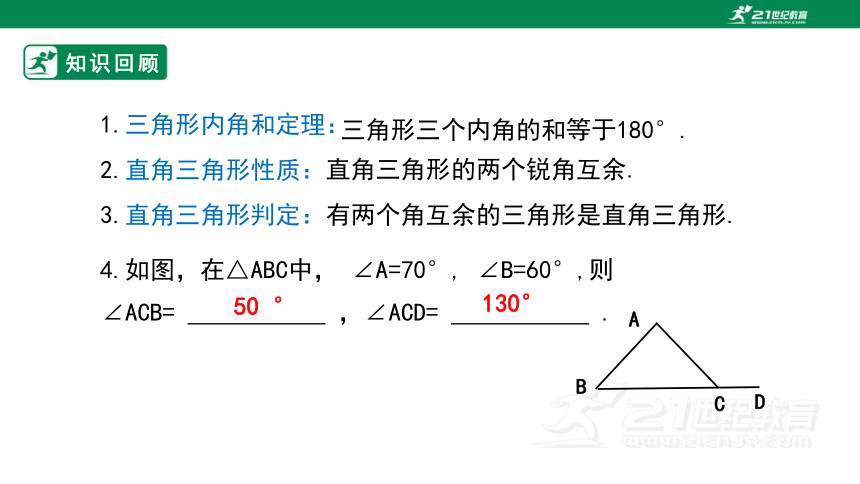
4.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
教学目标
1.了解三角形外角的概念.
2.理解三角形外角性质及三角形外角和的探究.
3.熟练掌握并运用三角形外角性质解决实际问题.
新知导入
4.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
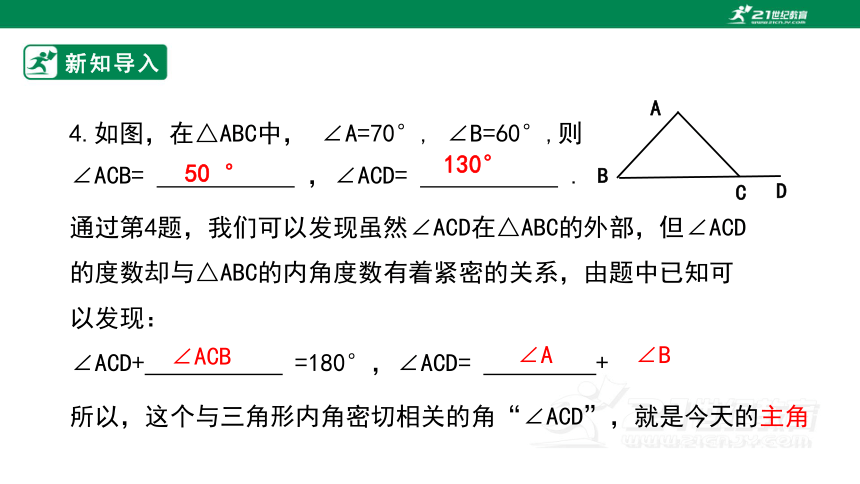
通过第4题,我们可以发现虽然∠ACD在△ABC的外部,但∠ACD的度数却与△ABC的内角度数有着紧密的关系,由题中已知可以发现:
∠ACD+ =180°,∠ACD= + .
∠A
∠B
∠ACB
所以,这个与三角形内角密切相关的角“∠ACD”,就是今天的主角
新知探究
知识点 1
三角形的外角的概念
A
B
C
D
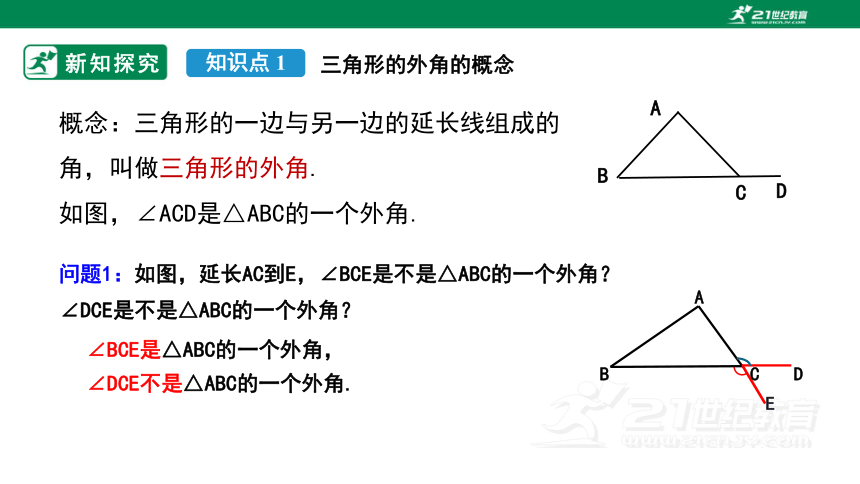
概念:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
如图,∠ACD是△ABC的一个外角.
问题1:如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
新知探究
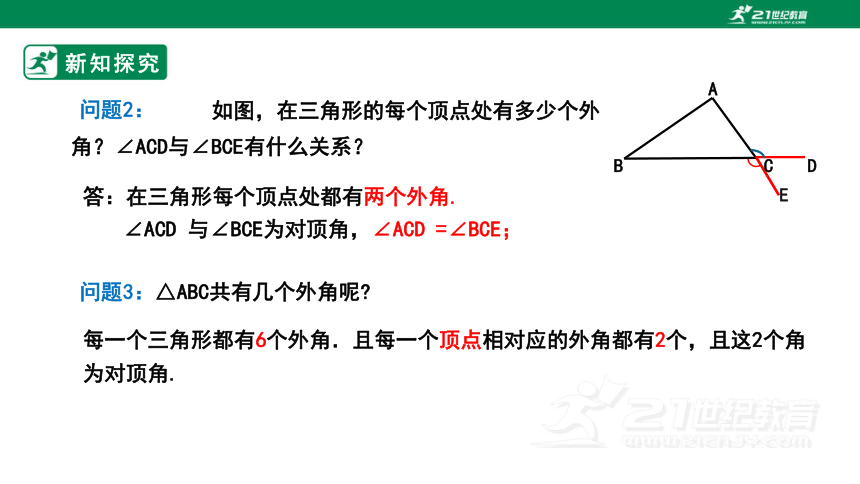
答:在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
如图,在三角形的每个顶点处有多少个外角?∠ACD与∠BCE有什么关系?
问题2:
E
C
B
A
D
问题3:△ABC共有几个外角呢
每一个三角形都有6个外角.且每一个顶点相对应的外角都有2个,且这2个角为对顶角.
新知探究
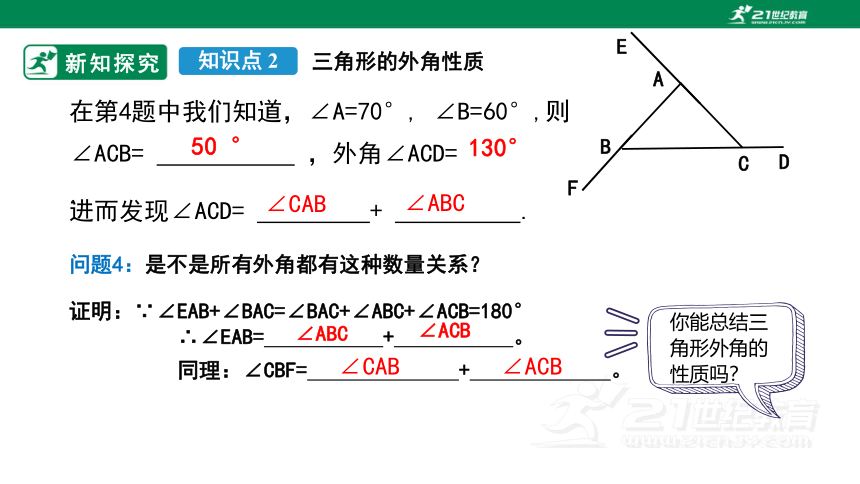
在第4题中我们知道,∠A=70°, ∠B=60°,则∠ACB= ,外角∠ACD= .
A
B
C
D
50 °
130°
进而发现∠ACD= + .
∠CAB
∠ABC
E
F
问题4:是不是所有外角都有这种数量关系?
证明:∵∠EAB+∠BAC=∠BAC+∠ABC+∠ACB=180°
∴∠EAB= + 。
同理:∠CBF= + 。
∠CAB
∠ACB
∠ABC
∠ACB
你能总结三角形外角的性质吗?
三角形的外角性质
知识点 2
新知小结
三角形外角的性质
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD= ∠A+ ∠B.
A
B
C
D
新知典例
例1.如图,∠A=65°,∠B=45°,则∠ACD=( )
A.65° B.60° C.45° D.110°
D
例2.如图,已知∠1=58°,∠B=60°,则∠2=( )
A.108° B.62° C.118° D.128°
C
新知典例
例3.如图,∠A=40°,∠ABD=38°,∠ACB=80°,且CD平分∠ACB,求∠BDC的度数.
A
B
C
D
解:延长BD交AC于点E
∵∠A=40°,∠ABD=38°,
∴∠BEC=∠A+∠ABD=40°+38°=78°,
∵CD平分∠ACB且∠ACB=80°
∴∠ACE= ∠ACB=40°,
∴∠BDC=∠EDC+∠DCE=78°+40°=118°
E
课堂练习
1.有一个零件如图所示,现已知∠A=10°,∠B=75°,∠C=15°,则∠ADC为多少度?
解:连接BD,设点E为BD延长线上一点,
∵∠ADE=∠A+∠ABD,∠CDE=∠C+∠CBD,
∴∠ADC=∠ADE+∠CDE,
=(∠A+∠ABD)+(∠C+∠CBD),
=∠A+∠C+(∠ABD+∠CBD),
=∠A+∠C+∠ABC,
∵∠A=10°,∠ABC=75°,∠C=15°
∴∠ADC=10°+15°+75°,
=100°.
F
如果延长AD与BC交于点F,这道题应该如何求解?
新知探究
三角形的外角和定理
知识点 3
三角形内角和为180°,那外角是否也有同样的情况呢?
如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
新知小结
三角形的三个外角和等于360°.
注意:三角形的每一个顶点处各有两个外角,三角形的外角和不是指六个外角的总和,而是说在三角形的每一个顶点处取一个外角,三个不同顶点处的外角和叫做三角形的外角和.
数学语言表示:
如图所示,∠CAD+∠CBE+∠BCF=360°.
三角形的外角和定理
A
B
E
F
C
D
1
2
3
新知典例
例4 下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
C
课堂练习
1.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠A的度数为( )
A.56° B.34° C.36° D.24°
B
课堂练习
2.一副三角板,按如图所示叠放在一起,则图中∠α的度数为( )
A.10° B.15° C.20° D.25°
B
课堂练习
3.一副三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.105° B.75° C.110° D.120°
B
课堂练习
4.将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠EDB= °.
75
解:∵∠ACB=90°,∠A=30°,
∴∠ABC=90°﹣30°=60°,
∵∠ABC=∠F+∠BDF,∠F=45°,
∴∠BDF=∠ABC﹣∠F=60°﹣45°=15°,
∵∠EDF=90°,
∴∠EDB=∠EDF﹣∠BDF=90°﹣15°=75°,
课堂练习
5.如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E,则∠E的度数为 .
45°
解:∵BE平分∠ABC,
∴∠ABE=
∵AF平分外角∠BAD,
∴∠FAB=
又∵∠BAD=∠C+∠ABC=90°+∠ABC,
∴∠FAB=
又∵∠FAB=∠E+∠ABE,
∴∠E=∠FAB﹣∠ABE=45°+ - =45°
课堂练习
6. 2016年2月6日凌晨,宝岛高雄发生6.7级地震,得知消息后,中国派出武警部队探测队,探测队探测出某建筑物下面有生命迹象,他们在生命迹象上方建筑物的一侧地面上的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),则∠C的度数是 .
30°
课堂练习
7.如图,∠ABC=∠ACB,AD,BD分别平分△ABC的外角∠EAC,内角∠ABC,求证:AD∥BC.
解:∵∠EAC为△ABC的外角,
∴∠EAC=∠ABC+∠ACB,
∵∠ABC=∠ACB,
∴∠EAC=2∠ACB,
∵AD平分∠EAC,
∴∠EAC=2∠DAC,
∴∠DAC=∠ACB,
∴AD∥BC.
∴∠E=∠4﹣∠2= (∠ACD﹣∠ABC)
= ∠A= ×58°=29°;
课堂练习
8.∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)若∠A=58°,求:∠E的度数.
(2)猜想∠A与∠E的关系,并说明理由.
解:(1)∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵BE平分∠ABC,CE平分∠ACD,
∴∠2= ∠ABC,∠4= ∠ACD,
课堂总结
三角形的外角
定义
性质
三角形
外角和
三角形的外角和等于360°
角的一边必须是三角形的一边,另一边必须是三角形的另一边的延长线
三角形的一个外角等于与其不相邻的两个内角的和
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.2 三角形的外角
人教版八年级上册
知识回顾
1.三角形内角和定理:
2.直角三角形性质:
3.直角三角形判定:
三角形三个内角的和等于180°.
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
4.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
教学目标
1.了解三角形外角的概念.
2.理解三角形外角性质及三角形外角和的探究.
3.熟练掌握并运用三角形外角性质解决实际问题.
新知导入
4.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
50 °
130°
通过第4题,我们可以发现虽然∠ACD在△ABC的外部,但∠ACD的度数却与△ABC的内角度数有着紧密的关系,由题中已知可以发现:
∠ACD+ =180°,∠ACD= + .
∠A
∠B
∠ACB
所以,这个与三角形内角密切相关的角“∠ACD”,就是今天的主角
新知探究
知识点 1
三角形的外角的概念
A
B
C
D
概念:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
如图,∠ACD是△ABC的一个外角.
问题1:如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
C
B
A
D
∠BCE是△ABC的一个外角,∠DCE不是△ABC的一个外角.
新知探究
答:在三角形每个顶点处都有两个外角.
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
如图,在三角形的每个顶点处有多少个外角?∠ACD与∠BCE有什么关系?
问题2:
E
C
B
A
D
问题3:△ABC共有几个外角呢
每一个三角形都有6个外角.且每一个顶点相对应的外角都有2个,且这2个角为对顶角.
新知探究
在第4题中我们知道,∠A=70°, ∠B=60°,则∠ACB= ,外角∠ACD= .
A
B
C
D
50 °
130°
进而发现∠ACD= + .
∠CAB
∠ABC
E
F
问题4:是不是所有外角都有这种数量关系?
证明:∵∠EAB+∠BAC=∠BAC+∠ABC+∠ACB=180°
∴∠EAB= + 。
同理:∠CBF= + 。
∠CAB
∠ACB
∠ABC
∠ACB
你能总结三角形外角的性质吗?
三角形的外角性质
知识点 2
新知小结
三角形外角的性质
三角形的外角等于与它不相邻的两个内角的和.
应用格式:
∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD= ∠A+ ∠B.
A
B
C
D
新知典例
例1.如图,∠A=65°,∠B=45°,则∠ACD=( )
A.65° B.60° C.45° D.110°
D
例2.如图,已知∠1=58°,∠B=60°,则∠2=( )
A.108° B.62° C.118° D.128°
C
新知典例
例3.如图,∠A=40°,∠ABD=38°,∠ACB=80°,且CD平分∠ACB,求∠BDC的度数.
A
B
C
D
解:延长BD交AC于点E
∵∠A=40°,∠ABD=38°,
∴∠BEC=∠A+∠ABD=40°+38°=78°,
∵CD平分∠ACB且∠ACB=80°
∴∠ACE= ∠ACB=40°,
∴∠BDC=∠EDC+∠DCE=78°+40°=118°
E
课堂练习
1.有一个零件如图所示,现已知∠A=10°,∠B=75°,∠C=15°,则∠ADC为多少度?
解:连接BD,设点E为BD延长线上一点,
∵∠ADE=∠A+∠ABD,∠CDE=∠C+∠CBD,
∴∠ADC=∠ADE+∠CDE,
=(∠A+∠ABD)+(∠C+∠CBD),
=∠A+∠C+(∠ABD+∠CBD),
=∠A+∠C+∠ABC,
∵∠A=10°,∠ABC=75°,∠C=15°
∴∠ADC=10°+15°+75°,
=100°.
F
如果延长AD与BC交于点F,这道题应该如何求解?
新知探究
三角形的外角和定理
知识点 3
三角形内角和为180°,那外角是否也有同样的情况呢?
如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
解:由三角形的一个外角等于与它不相邻的两个内角的和,得
∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,
∠ACD= ∠1+ ∠2.
又知∠1+ ∠2+ ∠3=180 °,
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
新知小结
三角形的三个外角和等于360°.
注意:三角形的每一个顶点处各有两个外角,三角形的外角和不是指六个外角的总和,而是说在三角形的每一个顶点处取一个外角,三个不同顶点处的外角和叫做三角形的外角和.
数学语言表示:
如图所示,∠CAD+∠CBE+∠BCF=360°.
三角形的外角和定理
A
B
E
F
C
D
1
2
3
新知典例
例4 下列对三角形的外角和叙述正确的是( )
A.三角形的外角和等于180°
B.三角形的外角和就是所有外角的和
C.三角形的外角和等于所有外角和的一半
D.以上都不对
C
课堂练习
1.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=58°,∠2=24°,则∠A的度数为( )
A.56° B.34° C.36° D.24°
B
课堂练习
2.一副三角板,按如图所示叠放在一起,则图中∠α的度数为( )
A.10° B.15° C.20° D.25°
B
课堂练习
3.一副三角板,按如图所示叠放在一起,则图中∠α的度数是( )
A.105° B.75° C.110° D.120°
B
课堂练习
4.将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠EDB= °.
75
解:∵∠ACB=90°,∠A=30°,
∴∠ABC=90°﹣30°=60°,
∵∠ABC=∠F+∠BDF,∠F=45°,
∴∠BDF=∠ABC﹣∠F=60°﹣45°=15°,
∵∠EDF=90°,
∴∠EDB=∠EDF﹣∠BDF=90°﹣15°=75°,
课堂练习
5.如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E,则∠E的度数为 .
45°
解:∵BE平分∠ABC,
∴∠ABE=
∵AF平分外角∠BAD,
∴∠FAB=
又∵∠BAD=∠C+∠ABC=90°+∠ABC,
∴∠FAB=
又∵∠FAB=∠E+∠ABE,
∴∠E=∠FAB﹣∠ABE=45°+ - =45°
课堂练习
6. 2016年2月6日凌晨,宝岛高雄发生6.7级地震,得知消息后,中国派出武警部队探测队,探测队探测出某建筑物下面有生命迹象,他们在生命迹象上方建筑物的一侧地面上的A,B两处,用仪器探测生命迹象C,已知探测线与地面的夹角分别是30°和60°(如图),则∠C的度数是 .
30°
课堂练习
7.如图,∠ABC=∠ACB,AD,BD分别平分△ABC的外角∠EAC,内角∠ABC,求证:AD∥BC.
解:∵∠EAC为△ABC的外角,
∴∠EAC=∠ABC+∠ACB,
∵∠ABC=∠ACB,
∴∠EAC=2∠ACB,
∵AD平分∠EAC,
∴∠EAC=2∠DAC,
∴∠DAC=∠ACB,
∴AD∥BC.
∴∠E=∠4﹣∠2= (∠ACD﹣∠ABC)
= ∠A= ×58°=29°;
课堂练习
8.∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)若∠A=58°,求:∠E的度数.
(2)猜想∠A与∠E的关系,并说明理由.
解:(1)∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵BE平分∠ABC,CE平分∠ACD,
∴∠2= ∠ABC,∠4= ∠ACD,
课堂总结
三角形的外角
定义
性质
三角形
外角和
三角形的外角和等于360°
角的一边必须是三角形的一边,另一边必须是三角形的另一边的延长线
三角形的一个外角等于与其不相邻的两个内角的和
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
