冀教版七年级上册 5.4 一元一次方程的应用课件(共37张PPT)
文档属性
| 名称 | 冀教版七年级上册 5.4 一元一次方程的应用课件(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 10:20:01 | ||
图片预览









文档简介
(共37张PPT)
一元一次方程的应用
思考:
1、将一个底面直径和高均为4m的圆柱形水箱,将其底面直径减少为3.2m,那么水箱增高多少米?
2、等量关系:
(圆柱的体积= )
3、如何根据等量关系列出方程?
旧水箱的容积=新水箱的容积
sh=πr h
旧水箱 新水箱
底面半径/m
高/m
容积/m
2
1.6
4
x
π×2 ×4
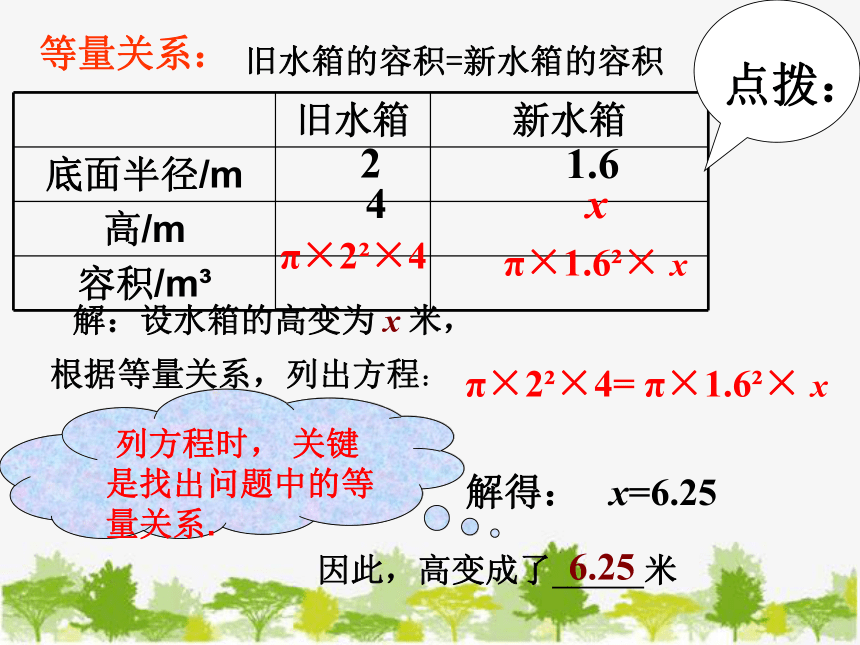
等量关系:
旧水箱的容积=新水箱的容积
根据等量关系,列出方程:
解得: x=6.25
6.25
因此,高变成了 米
列方程时, 关键是找出问题中的等量关系.
点拨:
π×1.6 × x
π×2 ×4= π×1.6 × x
解:设水箱的高变为 x 米,
我们可以把方程看做实际问题的一个数学模型.
用一根长为10米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
解:设此时长方形的宽为x米,
x+x+1.4=10÷2
2x=3.6
x=1.8
长方形的长为1.8+1.4=3.2
∴长方形的长为3.2米,宽为1.8米
则它的长为(x+1.4)米,
根据题意,得
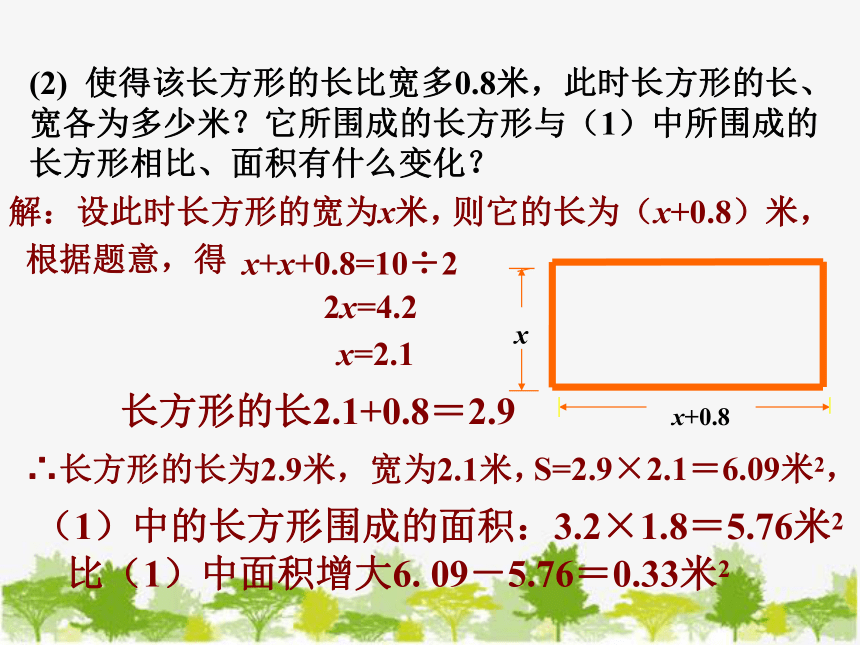
(2) 使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
解:设此时长方形的宽为x米,
x+x+0.8=10÷2
2x=4.2
x=2.1
长方形的长2.1+0.8=2.9
则它的长为(x+0.8)米,
根据题意,得
∴长方形的长为2.9米,宽为2.1米,
S=2.9×2.1=6.09米2,
(1)中的长方形围成的面积:3.2×1.8=5.76米2
比(1)中面积增大6. 09-5.76=0.33米2
x
x+0.8
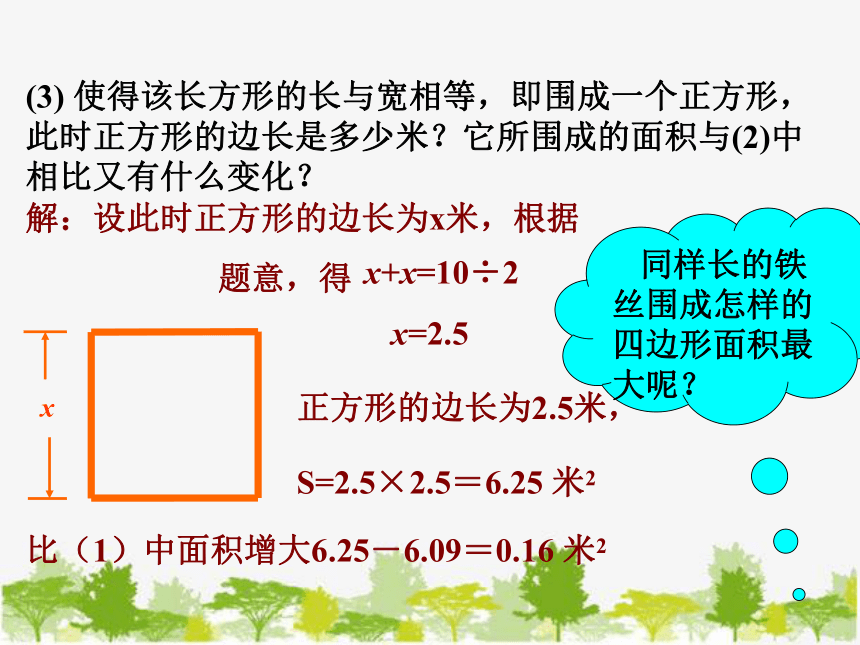
(3) 使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
解:设此时正方形的边长为x米,根据
题意,得
x+x=10÷2
x=2.5
比(1)中面积增大6.25-6.09=0.16 米2
x
正方形的边长为2.5米,
S=2.5×2.5=6.25 米2
同样长的铁丝围成怎样的四边形面积最大呢?
面积:1.8 × 3.2=5.76
面积:
2.9 ×2.1=6.09
面积:
2.5 × 2.5 =6. 25
围成正方形时面积最大
比较
小亮求出50个数据的平均数后,粗心地把这个平均数和原来的50个数据混写在一起,成为51个数据,忘记哪个是平均数了.如果这51个数据的平均数恰好为51,那么原来的50个平均数是多少?
解:设原来的50个平均数为x,则可列方程
50x+x=51×51,
解得x=51.
所以原来的50个平均数是51.
解:设每千克苹果的售价是x元.
根据题意,得
5x+2×2x =30-3.
解这个方程,得
x=3.
答:每千克苹果的售价是3元.
列方程解应用题:
1.小莹用30元钱买了5千克苹果和2千克香蕉,找回3元.已知每千克香蕉的售价是每千克苹果售价的2倍,每千克苹果的售价是多少元?
2.在一次竞赛中有A,B两组题,大刚平均1分钟做4道A组题,4分钟做1道B组题.他用了100分钟做了100道题,大刚做了多少道A组题?
(1)这个问题中的已知量是什么?未知量是什么?
(2)选取问题中的一个未知量并用x表示,利用表格表示出其他的未知量;
(3)题目中的等量关系是什么?
(4)列出方程并给出解答.
解:(1)已知量:平均1分钟做4道A组题,4分钟做1道B组题,100分钟做了100道题
未知量:A组题的道数及用得时间,B组题的道数及用得时间
(2)设做A组题用了x分钟,则
A组题/分钟 B组题/分钟
x 100-x
(3)A组题道数+B组题道数=总共100道题
(4)根据题意,得 4x+ (100-x)=100
解这个方程,得 x=20
4 ×20=80(道)
答:大刚做了80道A组题.
6人围坐成一圈,每人心中想一个数,并把这个数告诉左、右相邻的人.然后每个人把左、右两个相邻的人告诉自己的数的平均数亮出来(如图).问:亮出平均数是11的人原来心中想的数是多少?
解:设亮11的人心里想的是x,那么亮9的人心里想的数就是7×2-x=14-x;亮8的人心里想的数就是10×2-x=20-x,亮9和8中间的人报的数是4,所以: 14-x+20-x=4×2, 34-2x=8, 2x=26, x=13. 答:亮出11的人原来心中想的数是13.
列方程解应用题:
1.大小两台拖拉机共耕了5公顷土地.已知大拖拉机的效率是小拖拉机的1.5倍,两台拖拉机各耕地多少公顷?
解:设小拖拉机耕地x公顷.根据题意得
1.5x+x=5
解得 x=2
5-x=3
答:小拖拉机耕地2公顷,大拖拉机耕地3公顷.
2.水上公园某一天共售出门票128张,收入912元.门票价格为成人每张10元,学生可享受六折优惠.这一天出售的成人票与学生票各多少张?
解:设这一天出售的成人票x张,那么学生票售出(128-x)张.根据题意得
10x+10×60%(128-x)=912
解得 x=36
128-x=92
答:这一天出售的成人票36张,学生票92张.
小明每天早上要在7:50分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180米/分的速度去追小明.小明的爸爸能追上小明吗?
情景引入
(1) 爸爸追上小明用了多少时间?
(2) 追上小明时距离学校还有多远?
思考:
分析:设经x分钟后爸爸追上小明;
时 间 速 度 路 程
小 明
小明爸爸
等量关系: 小明走的路程=爸爸走的路程
80 (5 +x)米
180x米
80米/分钟
180米/分钟
(5+x)分钟
x分钟
解:(1)设经 x 分钟后爸爸追上小明,
根据题意,得
180 x = 80×5 + 80 x
解方程得: x = 4
(2)1000-180×4=280(米)
答:爸爸追上小明用了4分钟,此时
离学校 还有280米.
①追及问题:
男跑路程AC-女跑路程BC=相距路程AB
②相遇问题:
男跑路程AC+女跑路程BC=相距路程AB
A
B
C
A
B
C
行程问题
解决路程问题的关键是什么?
找出等量关系的重要方法是:
找出等量关系,列出方程.
画线段图.
列方程解应用题:
1.甲、乙两人从相距1 200米的两地同时出发,相向而行. 甲每分钟行70米,乙每分钟行50米,多少时间后两人相遇?
解:设两人x分钟后相遇,依题意可得
70x+50x=1200
解得 x=10
答:10分钟后两人相遇.
2.一队学生从学校出发去郊游,以4千米/时的速度步行前进.学生出发 时后,一位老师骑摩托车从原路经 时赶上学生.求摩托车的速度.
解:设摩托车的速度为x千米/时,依题意可得
x=4 × ( + )
解得 x=28
答:摩托车的速度为28千米/时.
列方程解应用题:
1.点燃两支等长的蜡烛,第一支4小时燃尽,第二支3小时燃尽.同时点燃两支蜡烛,几小时后第一支蜡烛剩余的高度是第二支蜡烛剩余高度的2倍?
解:设x小时后第一支蜡烛剩余的高度是第二支蜡烛剩余高度的2倍.
根据题意,得
1- x=2(1- x).
解这个方程,得
x=2.4.
答:2.4小时后第一支蜡烛剩余的高度是第二支蜡烛剩余高度的2倍.
2.维修一段管道,师傅单独维修需4小时完成,徒弟单独维修需6小时完成.如果徒弟先修30分钟,再与师傅一块维修,还需多少时间完成?
解:设还需x小时完成.
根据题意,得
× +( + )x=1.
解这个方程,得
x=2.2.
答:还需2.2小时完成.
1、500元的9折价是______元 ,x折是_______元.
2、某商品的每件销售利润是72元,进价是120,
则售价是__________元.
3、某商品利润率13﹪,进价为50元,则利润是
________元.
试一试
利润 = 售价-进价
打 x 折的售价=
利润率 =
进价
利润
原价×
450
192
6.5
例.一家商店将服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
仔细审题!
[分析]:若设每件衣服的成本价为x元,
那么每件衣服标价为__________元;
每件衣服的实际售价为______________ 元;
每件衣服的利润为__________________元.
由此,列出的方_____________________
解方程,得x=______
因此每件服装的成本____元.
(1+40%)x
(1+40%) ·x·80%
(1+40%) ·x·80%-x
(1+40%) ·x·80%-x=15
125
125
进价、售价、利润和利润率之间的关系是:
商品利润 = 商品售价 – 商品进价
商品的利润率 =
商品售价 – 商品进价
商品进价
1、进价为50元的商品,老板以60元的价格出售,其中的利润是___元.
2、某商品进价为500元,标价是800元,若打8折出售,则售价是____元,利润是________元,利润率是____.
3、一件商品,进价是200元,提高40﹪标价,则标价是________元,再以8.5折出售,则售价是________元,利润是________元,利润率是________.
尝试练习
10
640
140
28﹪
280
238
38
19﹪
如果例6的题目中的条件不变,除了可以求“每件商品的原价”之外,你还能提出一个新的问题吗?根据你提出的问题,列出一元一次方程求解,并与同学交流.
如果按原价的八折出售,则利润率又是多少?
设利润率为x,例题已经求出原价为2300元,
则可得
解得x=0.022.
所以按8折出售的利润率为2.2%.
1.填写下表:
商品名称 售价/元 进价/元 利润/元 利润率
钢笔 15 12
笔记本 8 3
文具盒 15 20%
3
25%
5
60%
3
18
2.李老师于2011年8月到银行将30000元现金存三年定期储蓄.在网上使用“存款利息计算器”计算可知,到期本息合计将共得34500元.三年定期储蓄的年利率是多少?
解:设三年定期储蓄的年利率是x.
根据题意,得
3×30000x+30000=34500.
解这个方程,得
x=5%.
答:三年定期储蓄的年利率是5%.
1.(1)如果三个连续奇数的和是81,求这三个连续奇数;
(2)如果三个连续奇数的和是47,求这三个连续奇数.
解(1)设第一个奇数是x .
根据题意,得 x+(x+2)+(x+4)=81.
解这个方程,得 x=25.
答:这三个连续奇数是25,27,29.
(2)设第一个奇数是x .
根据题意,得 x+(x+2)+(x+4)=47.
解这个方程,得 x= .
答:这三个连续奇数是 , , .
2.一种饮水机上的圆柱形水桶的内径为25厘米,内壁高为35厘米.有一个内径为6厘米,内壁高为10厘米的圆柱形玻璃杯,如果一桶饮用水全部用这个玻璃杯去盛,可以盛满多少杯?
解:设可以盛满x杯.
根据题意,得
π · 62×10 · x=π ·252×35
解这个方程,得
x ≈ 60.76.
答:可以盛满60杯.
2、找准数学模型.
1、列方程的关键是正确找出等量关系.
3、正确理解题意,并解答.
Byebye!
一元一次方程的应用
思考:
1、将一个底面直径和高均为4m的圆柱形水箱,将其底面直径减少为3.2m,那么水箱增高多少米?
2、等量关系:
(圆柱的体积= )
3、如何根据等量关系列出方程?
旧水箱的容积=新水箱的容积
sh=πr h
旧水箱 新水箱
底面半径/m
高/m
容积/m
2
1.6
4
x
π×2 ×4
等量关系:
旧水箱的容积=新水箱的容积
根据等量关系,列出方程:
解得: x=6.25
6.25
因此,高变成了 米
列方程时, 关键是找出问题中的等量关系.
点拨:
π×1.6 × x
π×2 ×4= π×1.6 × x
解:设水箱的高变为 x 米,
我们可以把方程看做实际问题的一个数学模型.
用一根长为10米的铁丝围成一个长方形.
(1)使得这个长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?
解:设此时长方形的宽为x米,
x+x+1.4=10÷2
2x=3.6
x=1.8
长方形的长为1.8+1.4=3.2
∴长方形的长为3.2米,宽为1.8米
则它的长为(x+1.4)米,
根据题意,得
(2) 使得该长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围成的长方形相比、面积有什么变化?
解:设此时长方形的宽为x米,
x+x+0.8=10÷2
2x=4.2
x=2.1
长方形的长2.1+0.8=2.9
则它的长为(x+0.8)米,
根据题意,得
∴长方形的长为2.9米,宽为2.1米,
S=2.9×2.1=6.09米2,
(1)中的长方形围成的面积:3.2×1.8=5.76米2
比(1)中面积增大6. 09-5.76=0.33米2
x
x+0.8
(3) 使得该长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少米?它所围成的面积与(2)中相比又有什么变化?
解:设此时正方形的边长为x米,根据
题意,得
x+x=10÷2
x=2.5
比(1)中面积增大6.25-6.09=0.16 米2
x
正方形的边长为2.5米,
S=2.5×2.5=6.25 米2
同样长的铁丝围成怎样的四边形面积最大呢?
面积:1.8 × 3.2=5.76
面积:
2.9 ×2.1=6.09
面积:
2.5 × 2.5 =6. 25
围成正方形时面积最大
比较
小亮求出50个数据的平均数后,粗心地把这个平均数和原来的50个数据混写在一起,成为51个数据,忘记哪个是平均数了.如果这51个数据的平均数恰好为51,那么原来的50个平均数是多少?
解:设原来的50个平均数为x,则可列方程
50x+x=51×51,
解得x=51.
所以原来的50个平均数是51.
解:设每千克苹果的售价是x元.
根据题意,得
5x+2×2x =30-3.
解这个方程,得
x=3.
答:每千克苹果的售价是3元.
列方程解应用题:
1.小莹用30元钱买了5千克苹果和2千克香蕉,找回3元.已知每千克香蕉的售价是每千克苹果售价的2倍,每千克苹果的售价是多少元?
2.在一次竞赛中有A,B两组题,大刚平均1分钟做4道A组题,4分钟做1道B组题.他用了100分钟做了100道题,大刚做了多少道A组题?
(1)这个问题中的已知量是什么?未知量是什么?
(2)选取问题中的一个未知量并用x表示,利用表格表示出其他的未知量;
(3)题目中的等量关系是什么?
(4)列出方程并给出解答.
解:(1)已知量:平均1分钟做4道A组题,4分钟做1道B组题,100分钟做了100道题
未知量:A组题的道数及用得时间,B组题的道数及用得时间
(2)设做A组题用了x分钟,则
A组题/分钟 B组题/分钟
x 100-x
(3)A组题道数+B组题道数=总共100道题
(4)根据题意,得 4x+ (100-x)=100
解这个方程,得 x=20
4 ×20=80(道)
答:大刚做了80道A组题.
6人围坐成一圈,每人心中想一个数,并把这个数告诉左、右相邻的人.然后每个人把左、右两个相邻的人告诉自己的数的平均数亮出来(如图).问:亮出平均数是11的人原来心中想的数是多少?
解:设亮11的人心里想的是x,那么亮9的人心里想的数就是7×2-x=14-x;亮8的人心里想的数就是10×2-x=20-x,亮9和8中间的人报的数是4,所以: 14-x+20-x=4×2, 34-2x=8, 2x=26, x=13. 答:亮出11的人原来心中想的数是13.
列方程解应用题:
1.大小两台拖拉机共耕了5公顷土地.已知大拖拉机的效率是小拖拉机的1.5倍,两台拖拉机各耕地多少公顷?
解:设小拖拉机耕地x公顷.根据题意得
1.5x+x=5
解得 x=2
5-x=3
答:小拖拉机耕地2公顷,大拖拉机耕地3公顷.
2.水上公园某一天共售出门票128张,收入912元.门票价格为成人每张10元,学生可享受六折优惠.这一天出售的成人票与学生票各多少张?
解:设这一天出售的成人票x张,那么学生票售出(128-x)张.根据题意得
10x+10×60%(128-x)=912
解得 x=36
128-x=92
答:这一天出售的成人票36张,学生票92张.
小明每天早上要在7:50分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180米/分的速度去追小明.小明的爸爸能追上小明吗?
情景引入
(1) 爸爸追上小明用了多少时间?
(2) 追上小明时距离学校还有多远?
思考:
分析:设经x分钟后爸爸追上小明;
时 间 速 度 路 程
小 明
小明爸爸
等量关系: 小明走的路程=爸爸走的路程
80 (5 +x)米
180x米
80米/分钟
180米/分钟
(5+x)分钟
x分钟
解:(1)设经 x 分钟后爸爸追上小明,
根据题意,得
180 x = 80×5 + 80 x
解方程得: x = 4
(2)1000-180×4=280(米)
答:爸爸追上小明用了4分钟,此时
离学校 还有280米.
①追及问题:
男跑路程AC-女跑路程BC=相距路程AB
②相遇问题:
男跑路程AC+女跑路程BC=相距路程AB
A
B
C
A
B
C
行程问题
解决路程问题的关键是什么?
找出等量关系的重要方法是:
找出等量关系,列出方程.
画线段图.
列方程解应用题:
1.甲、乙两人从相距1 200米的两地同时出发,相向而行. 甲每分钟行70米,乙每分钟行50米,多少时间后两人相遇?
解:设两人x分钟后相遇,依题意可得
70x+50x=1200
解得 x=10
答:10分钟后两人相遇.
2.一队学生从学校出发去郊游,以4千米/时的速度步行前进.学生出发 时后,一位老师骑摩托车从原路经 时赶上学生.求摩托车的速度.
解:设摩托车的速度为x千米/时,依题意可得
x=4 × ( + )
解得 x=28
答:摩托车的速度为28千米/时.
列方程解应用题:
1.点燃两支等长的蜡烛,第一支4小时燃尽,第二支3小时燃尽.同时点燃两支蜡烛,几小时后第一支蜡烛剩余的高度是第二支蜡烛剩余高度的2倍?
解:设x小时后第一支蜡烛剩余的高度是第二支蜡烛剩余高度的2倍.
根据题意,得
1- x=2(1- x).
解这个方程,得
x=2.4.
答:2.4小时后第一支蜡烛剩余的高度是第二支蜡烛剩余高度的2倍.
2.维修一段管道,师傅单独维修需4小时完成,徒弟单独维修需6小时完成.如果徒弟先修30分钟,再与师傅一块维修,还需多少时间完成?
解:设还需x小时完成.
根据题意,得
× +( + )x=1.
解这个方程,得
x=2.2.
答:还需2.2小时完成.
1、500元的9折价是______元 ,x折是_______元.
2、某商品的每件销售利润是72元,进价是120,
则售价是__________元.
3、某商品利润率13﹪,进价为50元,则利润是
________元.
试一试
利润 = 售价-进价
打 x 折的售价=
利润率 =
进价
利润
原价×
450
192
6.5
例.一家商店将服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
仔细审题!
[分析]:若设每件衣服的成本价为x元,
那么每件衣服标价为__________元;
每件衣服的实际售价为______________ 元;
每件衣服的利润为__________________元.
由此,列出的方_____________________
解方程,得x=______
因此每件服装的成本____元.
(1+40%)x
(1+40%) ·x·80%
(1+40%) ·x·80%-x
(1+40%) ·x·80%-x=15
125
125
进价、售价、利润和利润率之间的关系是:
商品利润 = 商品售价 – 商品进价
商品的利润率 =
商品售价 – 商品进价
商品进价
1、进价为50元的商品,老板以60元的价格出售,其中的利润是___元.
2、某商品进价为500元,标价是800元,若打8折出售,则售价是____元,利润是________元,利润率是____.
3、一件商品,进价是200元,提高40﹪标价,则标价是________元,再以8.5折出售,则售价是________元,利润是________元,利润率是________.
尝试练习
10
640
140
28﹪
280
238
38
19﹪
如果例6的题目中的条件不变,除了可以求“每件商品的原价”之外,你还能提出一个新的问题吗?根据你提出的问题,列出一元一次方程求解,并与同学交流.
如果按原价的八折出售,则利润率又是多少?
设利润率为x,例题已经求出原价为2300元,
则可得
解得x=0.022.
所以按8折出售的利润率为2.2%.
1.填写下表:
商品名称 售价/元 进价/元 利润/元 利润率
钢笔 15 12
笔记本 8 3
文具盒 15 20%
3
25%
5
60%
3
18
2.李老师于2011年8月到银行将30000元现金存三年定期储蓄.在网上使用“存款利息计算器”计算可知,到期本息合计将共得34500元.三年定期储蓄的年利率是多少?
解:设三年定期储蓄的年利率是x.
根据题意,得
3×30000x+30000=34500.
解这个方程,得
x=5%.
答:三年定期储蓄的年利率是5%.
1.(1)如果三个连续奇数的和是81,求这三个连续奇数;
(2)如果三个连续奇数的和是47,求这三个连续奇数.
解(1)设第一个奇数是x .
根据题意,得 x+(x+2)+(x+4)=81.
解这个方程,得 x=25.
答:这三个连续奇数是25,27,29.
(2)设第一个奇数是x .
根据题意,得 x+(x+2)+(x+4)=47.
解这个方程,得 x= .
答:这三个连续奇数是 , , .
2.一种饮水机上的圆柱形水桶的内径为25厘米,内壁高为35厘米.有一个内径为6厘米,内壁高为10厘米的圆柱形玻璃杯,如果一桶饮用水全部用这个玻璃杯去盛,可以盛满多少杯?
解:设可以盛满x杯.
根据题意,得
π · 62×10 · x=π ·252×35
解这个方程,得
x ≈ 60.76.
答:可以盛满60杯.
2、找准数学模型.
1、列方程的关键是正确找出等量关系.
3、正确理解题意,并解答.
Byebye!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
