2021-2022学年人教版数学七年级下册9.1.2不等式的性质 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册9.1.2不等式的性质 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 965.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 11:19:58 | ||
图片预览






文档简介
(共17张PPT)
第九章 不等式
9.1.2 不等式的性质
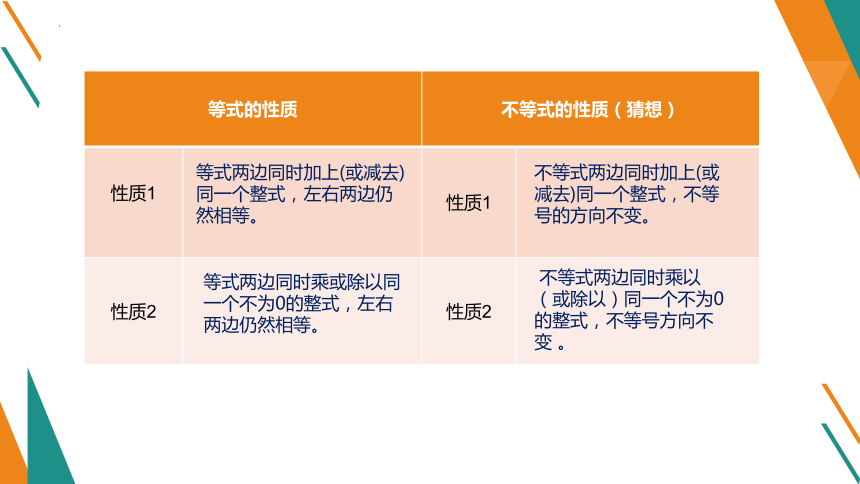
等式的性质 不等式的性质(猜想)
性质1 性质1
性质2 性质2
等式两边同时加上(或减去)同一个整式,左右两边仍然相等。
不等式两边同时加上(或减去)同一个整式,不等号的方向不变。
等式两边同时乘或除以同一个不为0的整式,左右两边仍然相等。
不等式两边同时乘以(或除以)同一个不为0的整式,不等号方向不变 。
思考
用“>”或“<”填空,并总结其中的规律
(1)
(2)
(3) -4>-7, -4+2_-7+2, -4-2_-7-2;
>
>
<
<
>
>
不改变
当不等式两边加或减同一个数(正数或负数)时,不等号的方向
一般的,不等式有以下性质
不等式性质1
不等式两边加(或减)同一个数
(或式子),不等号的方向不变。
(1)已知 a>b,则a+3 b+3.
(2)已知 a>
<
应用新知 用“>”或“<”填空:
(3)已知 a<
>
<
<
>
(4)
当不等式两边乘同一个正数时,不等号的方向
当不等式两边乘同一个负数时,不等号的方向
(5)
不改变
改变
用“>”或“<”填空,并总结其中的规律
那么这个规律是不是对所有的不等式都成立呢?我们换一些其他的数再来看一下
(1)
(2)
(3)
<
>
>
<
<
>
不等式性质2
不等式两边乘(或除以)同一个正数,
不等号的方向不变。
不等式性质3
不等式两边乘(或除以)同一个负数,
不等号的方向改变。
在数轴上分析
3>2
0
3
2
0
2
3
3×3
2×3
若x=3 3x( )2x
>
数轴上比较有理数大小的方法:
有理数越大,变负数之后,离原点的距离越远,在数轴上位置越在左边,数值也就越小
3×3
3
2
2×3
3×(-3)
2×(-3)
若x=-3 3x( )2x
<
小试牛刀
1.设a>b,那么下列不等式变形错误的是:
A. B.
C. D.
>
>
>
>
C
2.将下列不等式化成“x>a”或“x<a”的形式:
(1) X-5>-1 (2) -2x > 3
X-5+5>-1+5
解:
x>4
解:
-2x÷(-2) < 3÷(-2)
思考
已知:3>2
那么3x>2x(x≠0)一定成立吗?
?
课堂小结
不等式的性质
文字语言 符号语言
性质1 不等式两边加(或减)同一个数(或式 子),不等号的方向不变。
性质2 不等式两边乘(或除以)同一个正数, 不等号的方向不变。
性质3 不等式两边乘(或除以)同一个负数, 不等号的方向改变。
课后作业
P120 第4题,第6题
感谢观看
第九章 不等式
9.1.2 不等式的性质
等式的性质 不等式的性质(猜想)
性质1 性质1
性质2 性质2
等式两边同时加上(或减去)同一个整式,左右两边仍然相等。
不等式两边同时加上(或减去)同一个整式,不等号的方向不变。
等式两边同时乘或除以同一个不为0的整式,左右两边仍然相等。
不等式两边同时乘以(或除以)同一个不为0的整式,不等号方向不变 。
思考
用“>”或“<”填空,并总结其中的规律
(1)
(2)
(3) -4>-7, -4+2_-7+2, -4-2_-7-2;
>
>
<
<
>
>
不改变
当不等式两边加或减同一个数(正数或负数)时,不等号的方向
一般的,不等式有以下性质
不等式性质1
不等式两边加(或减)同一个数
(或式子),不等号的方向不变。
(1)已知 a>b,则a+3 b+3.
(2)已知 a
<
应用新知 用“>”或“<”填空:
(3)已知 a
>
<
<
>
(4)
当不等式两边乘同一个正数时,不等号的方向
当不等式两边乘同一个负数时,不等号的方向
(5)
不改变
改变
用“>”或“<”填空,并总结其中的规律
那么这个规律是不是对所有的不等式都成立呢?我们换一些其他的数再来看一下
(1)
(2)
(3)
<
>
>
<
<
>
不等式性质2
不等式两边乘(或除以)同一个正数,
不等号的方向不变。
不等式性质3
不等式两边乘(或除以)同一个负数,
不等号的方向改变。
在数轴上分析
3>2
0
3
2
0
2
3
3×3
2×3
若x=3 3x( )2x
>
数轴上比较有理数大小的方法:
有理数越大,变负数之后,离原点的距离越远,在数轴上位置越在左边,数值也就越小
3×3
3
2
2×3
3×(-3)
2×(-3)
若x=-3 3x( )2x
<
小试牛刀
1.设a>b,那么下列不等式变形错误的是:
A. B.
C. D.
>
>
>
>
C
2.将下列不等式化成“x>a”或“x<a”的形式:
(1) X-5>-1 (2) -2x > 3
X-5+5>-1+5
解:
x>4
解:
-2x÷(-2) < 3÷(-2)
思考
已知:3>2
那么3x>2x(x≠0)一定成立吗?
?
课堂小结
不等式的性质
文字语言 符号语言
性质1 不等式两边加(或减)同一个数(或式 子),不等号的方向不变。
性质2 不等式两边乘(或除以)同一个正数, 不等号的方向不变。
性质3 不等式两边乘(或除以)同一个负数, 不等号的方向改变。
课后作业
P120 第4题,第6题
感谢观看
