2.2 第2课时 去括号 课件(共22张PPT)
文档属性
| 名称 | 2.2 第2课时 去括号 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 16:25:01 | ||
图片预览








文档简介
(共22张PPT)
2.2 第2课时 去括号
人教版 七年级上册
教学目标
教学目标:
1. 理解去括号法则.
2. 会利用去括号法则将整式化简.
重点:1.能运用运算律探究去括号法则.
难点:2.会利用去括号法则将整式化简.
新知导入
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在
冻土地段、非冻土地段的行驶速度分别是100km/h和120km/h,列车通过
冻土地段比通过非冻土地段多用0.5h, 如果通过冻土地段需要u h, 则这段铁路的全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
新知导入
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在
冻土地段、非冻土地段的行驶速度分别是100km/h和120km/h,列车通过
冻土地段比通过非冻土地段多用0.5h, 如果通过冻土地段需要u h, 则这段铁路的全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
(u-0.5)
新知导入
(1)这段铁路的全长可以表示为:(单位:km)
(2)冻土地段与非冻土地段相差可以表示为:(单位:km)
100u + 120(u-0.5)
100u-120(u-0.5)
上面的式子都带有括号,它们应如何化简?
新知讲解
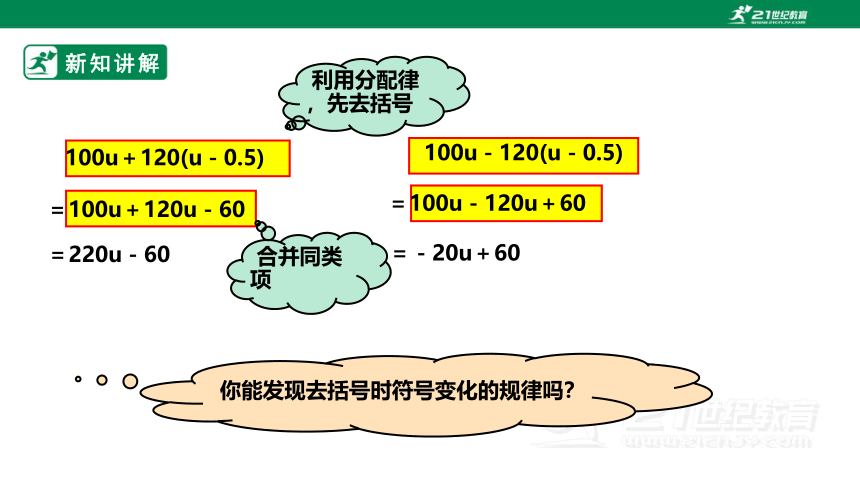
100u+120(u-0.5)
100u-120(u-0.5)
=100u+120u-60
=220u-60
=100u-120u+60
=-20u+60
利用分配律,先去括号
合并同类项
你能发现去括号时符号变化的规律吗?
新知讲解
去括号法则
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
巩固训练
(1)3(x+8)=3x+8
(2)–3(x–8)= –3x–24
(4)–2(6–x)= –12+2x
(3)4(–3–2x)= –12+8x
3x+3×8
错因:分配律,数字8漏乘3.
–3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
–12–8x
判一判
新知讲解
特别地(x-3)与-(x-3)应如何化简呢?
+(x-3)可以看作是1×(x-3)
-(x-3)可以看作是-1×(x-3)
+ (x-3)
=x-3
- (x-3)
=-x +3
去括号时括号内的每一项的符号都要考虑,做到要变都变,要不变则都不变;另外,括号内原来有几项,去掉括号后仍然有几项.
新知讲解
注意:
1.去括号时,要将括号连同它前面的符号一起去掉.
2.若括号前是“-”号,去括号时,括号内的各项都要变号,不能只改变括号内第一项或前几项的符号.
3.当括号前的因数不是±1时,要利用分配律将括号外的因数与括号内的每一项都相乘并去掉括号,不要漏乘括号内的任何一项.
新知讲解
去多重括号的方法
去多重括号时,一般由内向外,即先去小括号,再去中括号,最后去大括号;也可由外向内,即先去大括号,再去中括号,最后去小括号,且去大括号时,要将中括号看成一个整体,去中括号时,要将小括号看成一个整体.
新知讲解
解: (1)8a+2b+(5a-b)
=8a+2b +5a-b
=13a+b;
例1 化简下列各式:
(1)8a+2b+(5a-b);(2)(5a-3b)-3(a2-2b);
(2)(5a-3b)-3(a2-2b)
=+(5a-3b) -(3a2-6b)
=5a-3b -3a2+6b
=-3a2+5a+3b.
不变号
全变号
新知讲解
例2 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是a km/h.
(1)2 h后两船相距多远?
(2)2 h后甲船比乙船多航行多少千米?
解:顺水航速=船速+水速=(50+a) km/h,
逆水航速=船速-水速=(50-a) km/h.
(1) 2 h后两船相距(单位:km)
2(50+a)+2(50-a) = 100+2a+100-2a = 200.
(2) 2 h后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a) = 100+2a -100+2a = 4a.
课堂练习
1.下列等式中正确的是( )
A.2(a+1)=2a+1
B.-(a+b)=-a+b
C.-(a-b)=b-a
D.-(3-x)=3+x
2.下列各式中与a-b-c的值不相等的是( )
A.a-(b-c) B.a-(b+c)
C.(a-b)+(-c) D.(-c)-(b-a)
C
A
课堂练习
3.将-2(a-b)去括号得到的结果是( )
A.-2a+b B.-2a-b
C.-2a+2b D.-2a-2b
C
4.化简(a-b)-(a+b)的结果是( )
A.0 B.-2b C.2a D.2b
B
课堂练习
5.去掉下列各式中的括号:
(1)(x+y)-z=__________;
(2)x-(y+z)=____________;
(3)-1-2(x-y)= ________________;
(4)2(a-b)-3(x+y)= ________________________.
x+y-z
x-y-z
-1-2x+2y
2a-2b-3x-3y
课堂练习
6.化简:
(1)(x+2y)-(-2x+y);
解:原式=x+2y+2x-y=3x+y.
(2)(-b+3a)-2(a-b);
解:原式=-b+3a-2a+2b=a+b.
(3)3a2+2(a2-a)-4(a2-3a);
解:原式=3a2+2a2-2a-4a2+12a=a2+10a.
(4)2(-3a2+2a-1)-2(a2-3a-5).
解:原式=-6a2+4a-2-2a2+6a+10=-8a2+10a+8.
课堂练习
7.先化简,再求值:
(1)-3(3x2-2x+1)-3(-2x2-5x),其中x=-1;
解:原式=-9x2+6x-3+6x2+15x=-3x2+21x-3,
当x=-1时,原式=-3×(-1)2+21×(-1)-3=-3-21-3=-27.
(2)a-2[3a+b-2(a+b)],其中a=-20,b=10.
解:原式=a-2(3a+b-2a-2b)=a-2(a-b)=a-2a+2b=-a+2b.
当a=-20,b=10时,原式=-(-20)+2×10=40.
课堂练习
8.一个三角形的第一条边长为(x+2)cm,第二条边长比第一条边长小5 cm,第三条边长是第二条边长的2倍.
(1)用含x的式子表示这个三角形的周长;
(2)计算当x=6时这个三角形的周长.
解:(1)第二条边长为(x+2)-5=(x-3)cm,
第三条边长为2(x-3)=(2x-6)cm,
∴三角形的周长为(x+2)+(x-3)+(2x-6)=(4x-7)cm;
(2)当x=6时,三角形的周长为4x-7=24-7=17(cm).
课堂总结
去括号法则
括号前是“+”
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
括号前是“–”
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2 第2课时 去括号
人教版 七年级上册
教学目标
教学目标:
1. 理解去括号法则.
2. 会利用去括号法则将整式化简.
重点:1.能运用运算律探究去括号法则.
难点:2.会利用去括号法则将整式化简.
新知导入
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在
冻土地段、非冻土地段的行驶速度分别是100km/h和120km/h,列车通过
冻土地段比通过非冻土地段多用0.5h, 如果通过冻土地段需要u h, 则这段铁路的全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
新知导入
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在
冻土地段、非冻土地段的行驶速度分别是100km/h和120km/h,列车通过
冻土地段比通过非冻土地段多用0.5h, 如果通过冻土地段需要u h, 则这段铁路的全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
(u-0.5)
新知导入
(1)这段铁路的全长可以表示为:(单位:km)
(2)冻土地段与非冻土地段相差可以表示为:(单位:km)
100u + 120(u-0.5)
100u-120(u-0.5)
上面的式子都带有括号,它们应如何化简?
新知讲解
100u+120(u-0.5)
100u-120(u-0.5)
=100u+120u-60
=220u-60
=100u-120u+60
=-20u+60
利用分配律,先去括号
合并同类项
你能发现去括号时符号变化的规律吗?
新知讲解
去括号法则
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
巩固训练
(1)3(x+8)=3x+8
(2)–3(x–8)= –3x–24
(4)–2(6–x)= –12+2x
(3)4(–3–2x)= –12+8x
3x+3×8
错因:分配律,数字8漏乘3.
–3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
–12–8x
判一判
新知讲解
特别地(x-3)与-(x-3)应如何化简呢?
+(x-3)可以看作是1×(x-3)
-(x-3)可以看作是-1×(x-3)
+ (x-3)
=x-3
- (x-3)
=-x +3
去括号时括号内的每一项的符号都要考虑,做到要变都变,要不变则都不变;另外,括号内原来有几项,去掉括号后仍然有几项.
新知讲解
注意:
1.去括号时,要将括号连同它前面的符号一起去掉.
2.若括号前是“-”号,去括号时,括号内的各项都要变号,不能只改变括号内第一项或前几项的符号.
3.当括号前的因数不是±1时,要利用分配律将括号外的因数与括号内的每一项都相乘并去掉括号,不要漏乘括号内的任何一项.
新知讲解
去多重括号的方法
去多重括号时,一般由内向外,即先去小括号,再去中括号,最后去大括号;也可由外向内,即先去大括号,再去中括号,最后去小括号,且去大括号时,要将中括号看成一个整体,去中括号时,要将小括号看成一个整体.
新知讲解
解: (1)8a+2b+(5a-b)
=8a+2b +5a-b
=13a+b;
例1 化简下列各式:
(1)8a+2b+(5a-b);(2)(5a-3b)-3(a2-2b);
(2)(5a-3b)-3(a2-2b)
=+(5a-3b) -(3a2-6b)
=5a-3b -3a2+6b
=-3a2+5a+3b.
不变号
全变号
新知讲解
例2 两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50 km/h,水流速度是a km/h.
(1)2 h后两船相距多远?
(2)2 h后甲船比乙船多航行多少千米?
解:顺水航速=船速+水速=(50+a) km/h,
逆水航速=船速-水速=(50-a) km/h.
(1) 2 h后两船相距(单位:km)
2(50+a)+2(50-a) = 100+2a+100-2a = 200.
(2) 2 h后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a) = 100+2a -100+2a = 4a.
课堂练习
1.下列等式中正确的是( )
A.2(a+1)=2a+1
B.-(a+b)=-a+b
C.-(a-b)=b-a
D.-(3-x)=3+x
2.下列各式中与a-b-c的值不相等的是( )
A.a-(b-c) B.a-(b+c)
C.(a-b)+(-c) D.(-c)-(b-a)
C
A
课堂练习
3.将-2(a-b)去括号得到的结果是( )
A.-2a+b B.-2a-b
C.-2a+2b D.-2a-2b
C
4.化简(a-b)-(a+b)的结果是( )
A.0 B.-2b C.2a D.2b
B
课堂练习
5.去掉下列各式中的括号:
(1)(x+y)-z=__________;
(2)x-(y+z)=____________;
(3)-1-2(x-y)= ________________;
(4)2(a-b)-3(x+y)= ________________________.
x+y-z
x-y-z
-1-2x+2y
2a-2b-3x-3y
课堂练习
6.化简:
(1)(x+2y)-(-2x+y);
解:原式=x+2y+2x-y=3x+y.
(2)(-b+3a)-2(a-b);
解:原式=-b+3a-2a+2b=a+b.
(3)3a2+2(a2-a)-4(a2-3a);
解:原式=3a2+2a2-2a-4a2+12a=a2+10a.
(4)2(-3a2+2a-1)-2(a2-3a-5).
解:原式=-6a2+4a-2-2a2+6a+10=-8a2+10a+8.
课堂练习
7.先化简,再求值:
(1)-3(3x2-2x+1)-3(-2x2-5x),其中x=-1;
解:原式=-9x2+6x-3+6x2+15x=-3x2+21x-3,
当x=-1时,原式=-3×(-1)2+21×(-1)-3=-3-21-3=-27.
(2)a-2[3a+b-2(a+b)],其中a=-20,b=10.
解:原式=a-2(3a+b-2a-2b)=a-2(a-b)=a-2a+2b=-a+2b.
当a=-20,b=10时,原式=-(-20)+2×10=40.
课堂练习
8.一个三角形的第一条边长为(x+2)cm,第二条边长比第一条边长小5 cm,第三条边长是第二条边长的2倍.
(1)用含x的式子表示这个三角形的周长;
(2)计算当x=6时这个三角形的周长.
解:(1)第二条边长为(x+2)-5=(x-3)cm,
第三条边长为2(x-3)=(2x-6)cm,
∴三角形的周长为(x+2)+(x-3)+(2x-6)=(4x-7)cm;
(2)当x=6时,三角形的周长为4x-7=24-7=17(cm).
课堂总结
去括号法则
括号前是“+”
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
括号前是“–”
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
