2.2 第1课时 合并同类项 课件(共26张PPT)
文档属性
| 名称 | 2.2 第1课时 合并同类项 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 936.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 17:32:12 | ||
图片预览





文档简介
(共26张PPT)
2.2 第1课时 合并同类项
人教版 七年级上册
教学目标
教学目标:
1. 理解同类项的概念,会判断同类项.
2. 理解合并同类项的法则,会进行合并同类项.
3. 能在合并同类项的基础上进行化简、求值运算.
重点:知道同类项的概念,会识别同类项.
难点:掌握合并同类项的法则,并能准确合并同类项.
新知导入
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(用几个房间都可以)
新知讲解
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段. 列车在冻土地段、非冻土地段的行驶速度分别是100 km/h和120 km/h,请根据这些数据回答下列问题:
在西宁到拉萨路段,如果通过冻土地段的时间是t小时,那么它通过非冻土地段的时间是2.1t小时,这段路的全长(单位:千米)是100t+120×2.1t,
即100t+252t.
怎样化简这个式子呢?
新知讲解
(1)运用运算律计算:
100×2+252×2 = _________,
100×(-2)+252×(-2) = _________;
(2)根据(1)中的方法完成下面的运算,并说明其中的道理:
100t+252t = _________.
704
-704
352t
运用了分配律.
100t+252t=(100+252)t=352t
新知讲解
探究:
(1) 100t-252t =( ) t;
(2) 3x2+2x2=( ) x2;
(3) 3ab2-4ab2=( ) ab2.
上述运算有什么共同特点,你能从中得出什么规律?
-152
5
-1
新知讲解
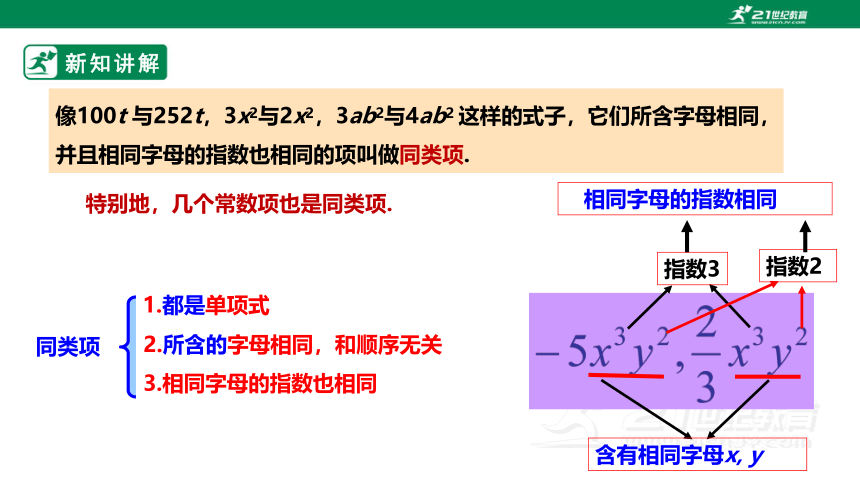
像100t 与252t,3x2与2x2,3ab2与4ab2 这样的式子,它们所含字母相同,并且相同字母的指数也相同的项叫做同类项.
特别地,几个常数项也是同类项.
含有相同字母x, y
指数3
指数2
相同字母的指数相同
2.所含的字母相同,和顺序无关
3.相同字母的指数也相同
同类项
1.都是单项式
新知讲解
化简:4x2+2x+7+3x-8x2-2.
解:4x2+2x+7+3x-8x2-2
=(4x2-8x2)+(2x+3x)+(7-2)
=(4x2-8x2)+(2x+3x)+(7-2)
=(4-8)x2+(2+3)x+(7-2)
=-4x2+5x+5.
交换律
结合律
逆用分配律
如何合并同类项
新知讲解
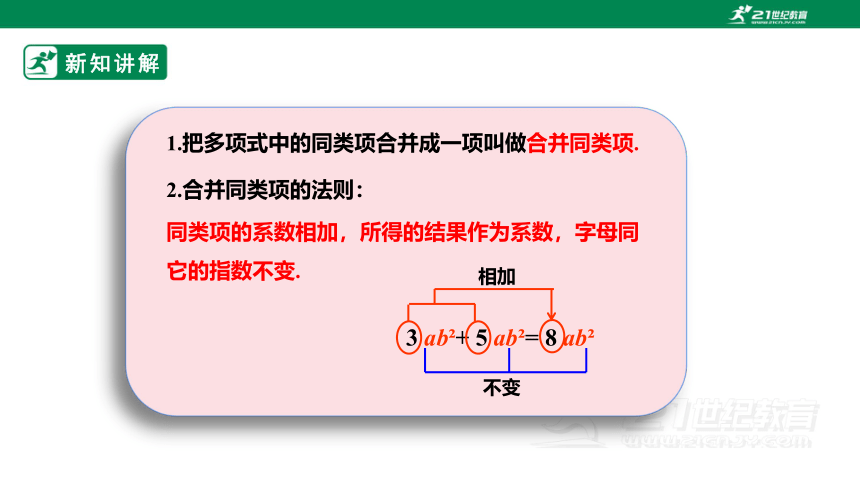
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母同它的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
3 ab + 5 ab = 8 ab
相加
不变
针对训练
下列合并同类项合并对了吗?不对的,说明理由.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
注:(2)(4)(5)中的单项式不是同类项,不能合并.
(3)是同类项,但合并结果不对.
新知讲解
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律、结合律,将不同类的同类项集中到不同的括号内;
三并,将同一括号内的同类项相加即可.
新知讲解
例1 合并下列各式的同类项:
(1)xy2- xy2;
(2)-3x2y+2x2y+3xy2 - 2xy2;
(3)4a2 + 3b2 +2ab-4a2 -4b2.
(3) 4a2 + 3b2 +2ab-4a2 -4b2
= (4a2-4a2) + ( 3b2 -4b2) + 2ab
= (4-4)a2 + (3-4)b2 + 2ab
=-b2 + 2ab.
(2) -3x2y+2x2y+3xy2 - 2xy2
=(-3+2)x2y+(3-2) xy2
=- x2y+xy2
新知讲解
合并同类项时要注意“一相加,两不变”:
“一相加”是指各同类项的系数相加;
“两不变”是指字母连同它的指数不变.
针对训练
下列各题计算的结果对不对?如果不对,指出错在哪里?
( )
( )
( )
( )
×
×
√
×
错因:不是同类项不能合并
错因:系数合并对了,但是字母和字母的指数不变
错因:不是同类项不能合并
新知讲解
例2 (1)求多项式 2x2-5x+x2+4x-3x2 -2 的值,其中x= ;
(2)求多项式 3a+abc - c2-3a+ c2 的值,其
中 a= b=2,c= -3.
分析:在求多项式的值时,可以先将多项式中的同类项合并,
然后再求值,这样做往往可以简化计算.
新知讲解
解: (1) 2x2-5x+x2+4x-3x2 -2
= (2+1-3) x2 + (-5+4) x-2
=-x-2.
新知讲解
例3 (1)水库中水位第一天连续下降了a h,每小时平均下降2 cm;
第二天连续上升了a h,每小时平均上升0.5 cm,这两天水位总的变化情况如何?
解:(1)把下降的水位变化量记为负,上升的水位变化量记为正。
第一天水位的变化量为-2acm,第二天的水位变化量是0.5acm.
两天水位的总变化量(单位:cm)是
-2a+0.5a=(-2+0.5)a=-1.5a
新知讲解
(2)某商店原有5袋大米,每袋大米为x kg.上午卖出3袋,下午又购进同样包装的大米4袋.进货后这个商店有大米多少千克?
(2)把进货的数量记为正,售出的数量记为负。进货后这个商店共有大米(单位:kg)是
5x-3x+4x=(5-3+4)x=6x
课堂练习
1.下列各式中,与-ab2是同类项的是( )
A.-3ab2 B.4a2b
C.3ab D.2a2b2
A
2. 下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
A
课堂练习
3.计算3x2-x2的结果是( )
A.2 B.2x2 C.2x D.4x2
B
合并同类项时,只需要系数相加,其他都不用变
4.若单项式 2x2ym 与-xny4可以合并成一项,则 nm = .
16
两个单项式能合并,说明这两个单项式是同类项.
课堂练习
5.合并下列各式的同类项:
(1)5m+2n-m-3n;
(2)3a2-1-2a-5+3a-a2;
(3)-5m2n+4mn2-2mn+6m2n+3mn.
解:原式=(5-1)m+(2-3)n=4m-n.
解:原式=(3-1)a2+(-2+3)a+(-1-5)=2a2+a-6.
解:原式=(-5+6)m2n+4mn2+(-2+3)mn=m2n+4mn2+mn.
课堂练习
6.求多项式4x2+2xy+9y2-2x2-3xy+y2的值,其中x=2,y=1.
解:4x2+2xy+9y2-2x2-3xy+y2
=(4-2)x2+(2-3)xy+(9+1)y2
=2x2-xy+10y2.
当x=2,y=1时, 原式=2×22-2×1+10×12=8-2+10=16.
课堂练习
7.某学校组织七、八年级全体学生参观革命老区西柏坡,七年级租用45座大巴车x辆,60座大巴车y辆,八年级租用60座大巴车x辆,30座中巴车y辆,每辆车恰好坐满.
(1)用含x,y的式子表示该学校七、八年级的总人数;
(2)当x=4,y=7时,该学校七、八年级共有多少学生?
解:(1)七、八年级的总人数为:45x+60y+60x+30y=105x+90y.
(2)当x=4,y=7时,105x+90y=105×4+90×7=1 050.所以该学校七、八年级共有1 050名学生.
课堂总结
同 类 项
合并同类项
两相同
法则
(1)字母相同,相同字母的指数相同;
(2)与系数无关,与字母的排列顺序无关.
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三并、四计算
(一加两不变)
两无关
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2 第1课时 合并同类项
人教版 七年级上册
教学目标
教学目标:
1. 理解同类项的概念,会判断同类项.
2. 理解合并同类项的法则,会进行合并同类项.
3. 能在合并同类项的基础上进行化简、求值运算.
重点:知道同类项的概念,会识别同类项.
难点:掌握合并同类项的法则,并能准确合并同类项.
新知导入
8n
-7a2b
3ab2
2a2b
6xy
5n
-3xy
-ab2
有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到不同的房间里吗?(用几个房间都可以)
新知讲解
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段. 列车在冻土地段、非冻土地段的行驶速度分别是100 km/h和120 km/h,请根据这些数据回答下列问题:
在西宁到拉萨路段,如果通过冻土地段的时间是t小时,那么它通过非冻土地段的时间是2.1t小时,这段路的全长(单位:千米)是100t+120×2.1t,
即100t+252t.
怎样化简这个式子呢?
新知讲解
(1)运用运算律计算:
100×2+252×2 = _________,
100×(-2)+252×(-2) = _________;
(2)根据(1)中的方法完成下面的运算,并说明其中的道理:
100t+252t = _________.
704
-704
352t
运用了分配律.
100t+252t=(100+252)t=352t
新知讲解
探究:
(1) 100t-252t =( ) t;
(2) 3x2+2x2=( ) x2;
(3) 3ab2-4ab2=( ) ab2.
上述运算有什么共同特点,你能从中得出什么规律?
-152
5
-1
新知讲解
像100t 与252t,3x2与2x2,3ab2与4ab2 这样的式子,它们所含字母相同,并且相同字母的指数也相同的项叫做同类项.
特别地,几个常数项也是同类项.
含有相同字母x, y
指数3
指数2
相同字母的指数相同
2.所含的字母相同,和顺序无关
3.相同字母的指数也相同
同类项
1.都是单项式
新知讲解
化简:4x2+2x+7+3x-8x2-2.
解:4x2+2x+7+3x-8x2-2
=(4x2-8x2)+(2x+3x)+(7-2)
=(4x2-8x2)+(2x+3x)+(7-2)
=(4-8)x2+(2+3)x+(7-2)
=-4x2+5x+5.
交换律
结合律
逆用分配律
如何合并同类项
新知讲解
2.合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母同它的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
3 ab + 5 ab = 8 ab
相加
不变
针对训练
下列合并同类项合并对了吗?不对的,说明理由.
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
×
√
×
×
×
√
注:(2)(4)(5)中的单项式不是同类项,不能合并.
(3)是同类项,但合并结果不对.
新知讲解
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律、结合律,将不同类的同类项集中到不同的括号内;
三并,将同一括号内的同类项相加即可.
新知讲解
例1 合并下列各式的同类项:
(1)xy2- xy2;
(2)-3x2y+2x2y+3xy2 - 2xy2;
(3)4a2 + 3b2 +2ab-4a2 -4b2.
(3) 4a2 + 3b2 +2ab-4a2 -4b2
= (4a2-4a2) + ( 3b2 -4b2) + 2ab
= (4-4)a2 + (3-4)b2 + 2ab
=-b2 + 2ab.
(2) -3x2y+2x2y+3xy2 - 2xy2
=(-3+2)x2y+(3-2) xy2
=- x2y+xy2
新知讲解
合并同类项时要注意“一相加,两不变”:
“一相加”是指各同类项的系数相加;
“两不变”是指字母连同它的指数不变.
针对训练
下列各题计算的结果对不对?如果不对,指出错在哪里?
( )
( )
( )
( )
×
×
√
×
错因:不是同类项不能合并
错因:系数合并对了,但是字母和字母的指数不变
错因:不是同类项不能合并
新知讲解
例2 (1)求多项式 2x2-5x+x2+4x-3x2 -2 的值,其中x= ;
(2)求多项式 3a+abc - c2-3a+ c2 的值,其
中 a= b=2,c= -3.
分析:在求多项式的值时,可以先将多项式中的同类项合并,
然后再求值,这样做往往可以简化计算.
新知讲解
解: (1) 2x2-5x+x2+4x-3x2 -2
= (2+1-3) x2 + (-5+4) x-2
=-x-2.
新知讲解
例3 (1)水库中水位第一天连续下降了a h,每小时平均下降2 cm;
第二天连续上升了a h,每小时平均上升0.5 cm,这两天水位总的变化情况如何?
解:(1)把下降的水位变化量记为负,上升的水位变化量记为正。
第一天水位的变化量为-2acm,第二天的水位变化量是0.5acm.
两天水位的总变化量(单位:cm)是
-2a+0.5a=(-2+0.5)a=-1.5a
新知讲解
(2)某商店原有5袋大米,每袋大米为x kg.上午卖出3袋,下午又购进同样包装的大米4袋.进货后这个商店有大米多少千克?
(2)把进货的数量记为正,售出的数量记为负。进货后这个商店共有大米(单位:kg)是
5x-3x+4x=(5-3+4)x=6x
课堂练习
1.下列各式中,与-ab2是同类项的是( )
A.-3ab2 B.4a2b
C.3ab D.2a2b2
A
2. 下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
A
课堂练习
3.计算3x2-x2的结果是( )
A.2 B.2x2 C.2x D.4x2
B
合并同类项时,只需要系数相加,其他都不用变
4.若单项式 2x2ym 与-xny4可以合并成一项,则 nm = .
16
两个单项式能合并,说明这两个单项式是同类项.
课堂练习
5.合并下列各式的同类项:
(1)5m+2n-m-3n;
(2)3a2-1-2a-5+3a-a2;
(3)-5m2n+4mn2-2mn+6m2n+3mn.
解:原式=(5-1)m+(2-3)n=4m-n.
解:原式=(3-1)a2+(-2+3)a+(-1-5)=2a2+a-6.
解:原式=(-5+6)m2n+4mn2+(-2+3)mn=m2n+4mn2+mn.
课堂练习
6.求多项式4x2+2xy+9y2-2x2-3xy+y2的值,其中x=2,y=1.
解:4x2+2xy+9y2-2x2-3xy+y2
=(4-2)x2+(2-3)xy+(9+1)y2
=2x2-xy+10y2.
当x=2,y=1时, 原式=2×22-2×1+10×12=8-2+10=16.
课堂练习
7.某学校组织七、八年级全体学生参观革命老区西柏坡,七年级租用45座大巴车x辆,60座大巴车y辆,八年级租用60座大巴车x辆,30座中巴车y辆,每辆车恰好坐满.
(1)用含x,y的式子表示该学校七、八年级的总人数;
(2)当x=4,y=7时,该学校七、八年级共有多少学生?
解:(1)七、八年级的总人数为:45x+60y+60x+30y=105x+90y.
(2)当x=4,y=7时,105x+90y=105×4+90×7=1 050.所以该学校七、八年级共有1 050名学生.
课堂总结
同 类 项
合并同类项
两相同
法则
(1)字母相同,相同字母的指数相同;
(2)与系数无关,与字母的排列顺序无关.
(1)系数相加;
(2)字母连同它的指数不变.
步骤
一找、二移、三并、四计算
(一加两不变)
两无关
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
