2.6.2 有理数加法的运算律 课件(共21张PPT)
文档属性
| 名称 | 2.6.2 有理数加法的运算律 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 16:54:22 | ||
图片预览








文档简介
(共21张PPT)
2.6.2 有理数加法的运算律
华师大版 七年级上册
教学目标
【教学目标】
1.让学生能运用加法运算律简化加法运算;
2.让学生理解加法运算律在加法运算中的作用,适当进行推理训练;
3.培养分类与归纳能力,强化学生的数形结合思想,提高学生的自学能力及理解能力,激发学生学习数学的兴趣.
【重点】有理数加法的运算律,并能运用加法运算律简化运算.
【难点】灵活运用加法运算律简化运算.
新知导入
在小学,我们学过的加法运算律都有哪些?
加法交换律:
加法结合律:
例如(1) 5 +3.5 = 3.5+5 ;
(2)(5+3.5)+ 2.5 = 5 +(3.5+2.5).
引进负数以后,以前学过的加法运算律还适用吗?
新知讲解
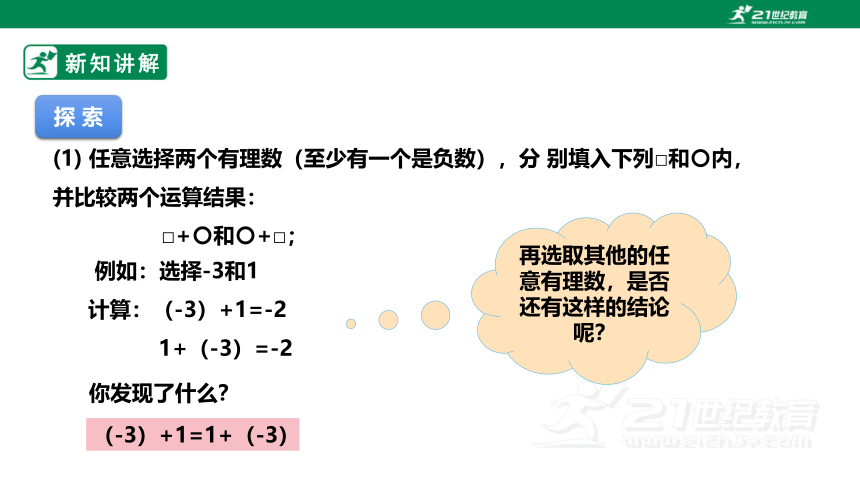
(1) 任意选择两个有理数(至少有一个是负数),分 别填入下列□和〇内,并比较两个运算结果:
□+〇和〇+□;
探 索
例如:选择-3和1
计算:(-3)+1=-2
1+(-3)=-2
再选取其他的任意有理数,是否还有这样的结论呢?
你发现了什么?
(-3)+1=1+(-3)
新知讲解
有理数的加法中,
两个数相加,交换加数的位置,和不变.
加法交换律: .
.加法交换律
新知讲解
(2) 任意选择三个有理数(至少有一个是负数),分别填入下列□、〇和 内,并比较两个运算结果:
(□+〇)+ 和□+(〇+ ).
例如:(4+5)+(-3)=9+(-3)=6
4+[5+(-3)]=4+2=6
你发现了什么?
(4+5)+(-3)=4+[5+(-3)]
再选取其他的任意有理数,是否还有这样的结论呢?
探 索
新知讲解
有理数的加法中,
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律: .
.加法结合律
新知讲解
有理数的加法仍满足交换律和结合律
加法交换律 : 两个数相加,交换加数的位置,和不变。
a+b=b+a
加法结合律:三个数相加,先把前两个数相加或者
先把后两个数相加,和不变。
(a+b)+c=a+(b+c)
针对训练
根据加法的交换律和结合律,在式子中填出相应的数.
(1)-4+_______=(-15)+___________;
(2) (-1.75)+12+(-0.25)=12+[(-1.75)+________ ];
(3)(-2.28)+3.7+(-3.72)+6.3
=[(-2.28)+(_______)]+[3.7+____ ].
(-15)
(-4)
(-0.25)
-3.72
6.3
新知讲解
例2 计算
(1) (+26)+(-18)+5+(-16)
(2) (-1.75) +1.5 +(+7.3) +(-2.25) +(-8.5)
解:(1)(+26)+(-18)+5+(-16)
=(26 +5) + [(-18) + (- 16) ]
= 31 + (-34)
= - (34 -31)
=-3
新知讲解
例2 计算
(1) (+26)+(-18)+5+(-16)
(2) (-1.75) +1.5 +(+7.3) +(-2.25) +(-8.5)
(2) (-1.75) + 1.5 + (+7.3) + (-2.25) + (-8.5)
= [(-1.75) +(-2.25)] + [1.5 + (-8.5)] + 7.3
= (-4)+(-7) +7.3
= (-4) +[(-7) + 7.3]
= (-4) +0.3
=-3.7
相加能凑成整数的数相加,即“凑整法”
新知讲解
例3 10筐苹果,以每筐30千克为基准,超过的千克数记作正数,
不足的千克数记作负数,记录如下:
2,-4, 2.5, 3, -0.5, 1.5, 3, - 1, 0, -2.5.
问这10筐苹果总共重多少
解:2 + (-4) +2.5 +3 + (-0.5) +1.5+3 +(-1) +0 + (-2.5)
= (2 +3 +3) +(-4) +[2.5 + (-2.5)] +[(-0.5) + (-1) + 1.5]
= 8+(-4)=4.
30×10+4=304(千克).
答 : 这筐苹果总共重 304 千克.
互为相反数的两个数先相加-------“相反数结合法”
回顾例2、例3的解答,思考:将怎样的加数结合在一起,可使运算简便?
1.符号相同的数先相加------“同号结合法”.
2.相加能得到整数的数先相加----“凑整法”.
3.互为相反数的两个数先相加-------“相反数结合法”.
4.分母相同的数先相加------“同形结合法”.
5.带分数相加时,先拆分成整数和真分数的和,再利用加法的运算律进行相加-----“拆项结合法”.
总结归纳
新知讲解
课堂练习
1.运用运算律计算3+(-7)+5+(-3)+2+(-4)+6,错误的是( )
A.[3+(-3)]+[(-7)+5+2]+[(-4)+6]
B.(3+5+2+6)+[(-7)+(-3)+(-4)]
C.(3+5+2)+[(-7)+(-3)]+[(-4)+6]
D.(3+5+2)+(7+3)+[(-4)+6]
D
2.计算6+(-3.5)+(+2.5)时,较好的方法是( )
A.按顺序进行计算 B.同号的数先相加
C.后面的两个数先相加 D.以上的方法都不对
C
课堂练习
3.若a、b互为相反数,则|a+(-3)+b|=____.
4.若三个数的和大于0,则( )
A.三个数中至少有两个正数
B.三个数中有且只有一个正数
C.三个数中有两个是正数或有两个是负数
D.三个数中至少有一个是正数
-3
D
课堂练习
5.计算:
(1)23+(-17)+6+(-22)
=(23+6)+[(-27)+(-22)]
=29-49
=-20
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-5
(2)(-2)+3+1+(-3)+2+(-4)
课堂练习
6.计算:
=-2
课堂练习
7.10袋大米,以每袋50千克为基准,超过的千克数记作正数,不足的千克数记作负数,称重的记录如下(单位:千克):
+0.5,+0.3,0,-0.2,-0.3,+1.1,-0.7,-0.2,+0.6,+0.7.
这10袋大米共超重(或不足)多少千克?总质量是多少千克?
解:(+0.5)+(+0.3)+0+(-0.2)+(-0.3)+(+1.1)+(-0.7)+(-0.2)+(+0.6)+(+0.7)=1.8(千克),
50×10+1.8=501.8(千克).
即这10袋大米共超重1.8千克,总质量是501.8千克.
课堂总结
1.有理数的加法交换律和结合律
加法交换律 : 两个数相加,交换加数的位置,和不变。a+b=b+a
加法结合律:三个数相加,先把前两个数相加或者先把后两个数相加,和不变。
(a+b)+c=a+(b+c)
(1)符号相同的数先相加------“同号结合法”.
(2)相加能得到整数的数先相加----“凑整法”.
(3)互为相反数的两个数先相加-------“相反数结合法”.
(4)分母相同的数先相加------“同形结合法”.
(5)带分数相加时,先拆分成整数和真分数的和,再利用加法的运算律进行相加-----“拆项结合法”.
2.有理数的加法计算常用简便方法:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.6.2 有理数加法的运算律
华师大版 七年级上册
教学目标
【教学目标】
1.让学生能运用加法运算律简化加法运算;
2.让学生理解加法运算律在加法运算中的作用,适当进行推理训练;
3.培养分类与归纳能力,强化学生的数形结合思想,提高学生的自学能力及理解能力,激发学生学习数学的兴趣.
【重点】有理数加法的运算律,并能运用加法运算律简化运算.
【难点】灵活运用加法运算律简化运算.
新知导入
在小学,我们学过的加法运算律都有哪些?
加法交换律:
加法结合律:
例如(1) 5 +3.5 = 3.5+5 ;
(2)(5+3.5)+ 2.5 = 5 +(3.5+2.5).
引进负数以后,以前学过的加法运算律还适用吗?
新知讲解
(1) 任意选择两个有理数(至少有一个是负数),分 别填入下列□和〇内,并比较两个运算结果:
□+〇和〇+□;
探 索
例如:选择-3和1
计算:(-3)+1=-2
1+(-3)=-2
再选取其他的任意有理数,是否还有这样的结论呢?
你发现了什么?
(-3)+1=1+(-3)
新知讲解
有理数的加法中,
两个数相加,交换加数的位置,和不变.
加法交换律: .
.加法交换律
新知讲解
(2) 任意选择三个有理数(至少有一个是负数),分别填入下列□、〇和 内,并比较两个运算结果:
(□+〇)+ 和□+(〇+ ).
例如:(4+5)+(-3)=9+(-3)=6
4+[5+(-3)]=4+2=6
你发现了什么?
(4+5)+(-3)=4+[5+(-3)]
再选取其他的任意有理数,是否还有这样的结论呢?
探 索
新知讲解
有理数的加法中,
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律: .
.加法结合律
新知讲解
有理数的加法仍满足交换律和结合律
加法交换律 : 两个数相加,交换加数的位置,和不变。
a+b=b+a
加法结合律:三个数相加,先把前两个数相加或者
先把后两个数相加,和不变。
(a+b)+c=a+(b+c)
针对训练
根据加法的交换律和结合律,在式子中填出相应的数.
(1)-4+_______=(-15)+___________;
(2) (-1.75)+12+(-0.25)=12+[(-1.75)+________ ];
(3)(-2.28)+3.7+(-3.72)+6.3
=[(-2.28)+(_______)]+[3.7+____ ].
(-15)
(-4)
(-0.25)
-3.72
6.3
新知讲解
例2 计算
(1) (+26)+(-18)+5+(-16)
(2) (-1.75) +1.5 +(+7.3) +(-2.25) +(-8.5)
解:(1)(+26)+(-18)+5+(-16)
=(26 +5) + [(-18) + (- 16) ]
= 31 + (-34)
= - (34 -31)
=-3
新知讲解
例2 计算
(1) (+26)+(-18)+5+(-16)
(2) (-1.75) +1.5 +(+7.3) +(-2.25) +(-8.5)
(2) (-1.75) + 1.5 + (+7.3) + (-2.25) + (-8.5)
= [(-1.75) +(-2.25)] + [1.5 + (-8.5)] + 7.3
= (-4)+(-7) +7.3
= (-4) +[(-7) + 7.3]
= (-4) +0.3
=-3.7
相加能凑成整数的数相加,即“凑整法”
新知讲解
例3 10筐苹果,以每筐30千克为基准,超过的千克数记作正数,
不足的千克数记作负数,记录如下:
2,-4, 2.5, 3, -0.5, 1.5, 3, - 1, 0, -2.5.
问这10筐苹果总共重多少
解:2 + (-4) +2.5 +3 + (-0.5) +1.5+3 +(-1) +0 + (-2.5)
= (2 +3 +3) +(-4) +[2.5 + (-2.5)] +[(-0.5) + (-1) + 1.5]
= 8+(-4)=4.
30×10+4=304(千克).
答 : 这筐苹果总共重 304 千克.
互为相反数的两个数先相加-------“相反数结合法”
回顾例2、例3的解答,思考:将怎样的加数结合在一起,可使运算简便?
1.符号相同的数先相加------“同号结合法”.
2.相加能得到整数的数先相加----“凑整法”.
3.互为相反数的两个数先相加-------“相反数结合法”.
4.分母相同的数先相加------“同形结合法”.
5.带分数相加时,先拆分成整数和真分数的和,再利用加法的运算律进行相加-----“拆项结合法”.
总结归纳
新知讲解
课堂练习
1.运用运算律计算3+(-7)+5+(-3)+2+(-4)+6,错误的是( )
A.[3+(-3)]+[(-7)+5+2]+[(-4)+6]
B.(3+5+2+6)+[(-7)+(-3)+(-4)]
C.(3+5+2)+[(-7)+(-3)]+[(-4)+6]
D.(3+5+2)+(7+3)+[(-4)+6]
D
2.计算6+(-3.5)+(+2.5)时,较好的方法是( )
A.按顺序进行计算 B.同号的数先相加
C.后面的两个数先相加 D.以上的方法都不对
C
课堂练习
3.若a、b互为相反数,则|a+(-3)+b|=____.
4.若三个数的和大于0,则( )
A.三个数中至少有两个正数
B.三个数中有且只有一个正数
C.三个数中有两个是正数或有两个是负数
D.三个数中至少有一个是正数
-3
D
课堂练习
5.计算:
(1)23+(-17)+6+(-22)
=(23+6)+[(-27)+(-22)]
=29-49
=-20
=(3+1+2)+[(-2)+(-3)+(-4)]
=6-9
=-5
(2)(-2)+3+1+(-3)+2+(-4)
课堂练习
6.计算:
=-2
课堂练习
7.10袋大米,以每袋50千克为基准,超过的千克数记作正数,不足的千克数记作负数,称重的记录如下(单位:千克):
+0.5,+0.3,0,-0.2,-0.3,+1.1,-0.7,-0.2,+0.6,+0.7.
这10袋大米共超重(或不足)多少千克?总质量是多少千克?
解:(+0.5)+(+0.3)+0+(-0.2)+(-0.3)+(+1.1)+(-0.7)+(-0.2)+(+0.6)+(+0.7)=1.8(千克),
50×10+1.8=501.8(千克).
即这10袋大米共超重1.8千克,总质量是501.8千克.
课堂总结
1.有理数的加法交换律和结合律
加法交换律 : 两个数相加,交换加数的位置,和不变。a+b=b+a
加法结合律:三个数相加,先把前两个数相加或者先把后两个数相加,和不变。
(a+b)+c=a+(b+c)
(1)符号相同的数先相加------“同号结合法”.
(2)相加能得到整数的数先相加----“凑整法”.
(3)互为相反数的两个数先相加-------“相反数结合法”.
(4)分母相同的数先相加------“同形结合法”.
(5)带分数相加时,先拆分成整数和真分数的和,再利用加法的运算律进行相加-----“拆项结合法”.
2.有理数的加法计算常用简便方法:
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
