湖南省衡山县第二中学2022-2023学年高一上学期8月入学考试数学试题(Word版含答案)
文档属性
| 名称 | 湖南省衡山县第二中学2022-2023学年高一上学期8月入学考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 229.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 18:04:34 | ||
图片预览


文档简介
衡山县第二中学2022-2023学年高一上学期8月入学考试
数学试卷
第I卷(选择题)
一、单选题(每小题3分,共33分)
1.下列结论成立的是( ).
A.若,则 B.若,则
C.若,则 D.若,则
2.随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元.将数据“2684”用科学记数法表示( )
A. B. C. D.
3.下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. B. C. D.
4.是某三角形三边的长,则等于( )
A. B. C.10 D.4
5.已知点在第三象限,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
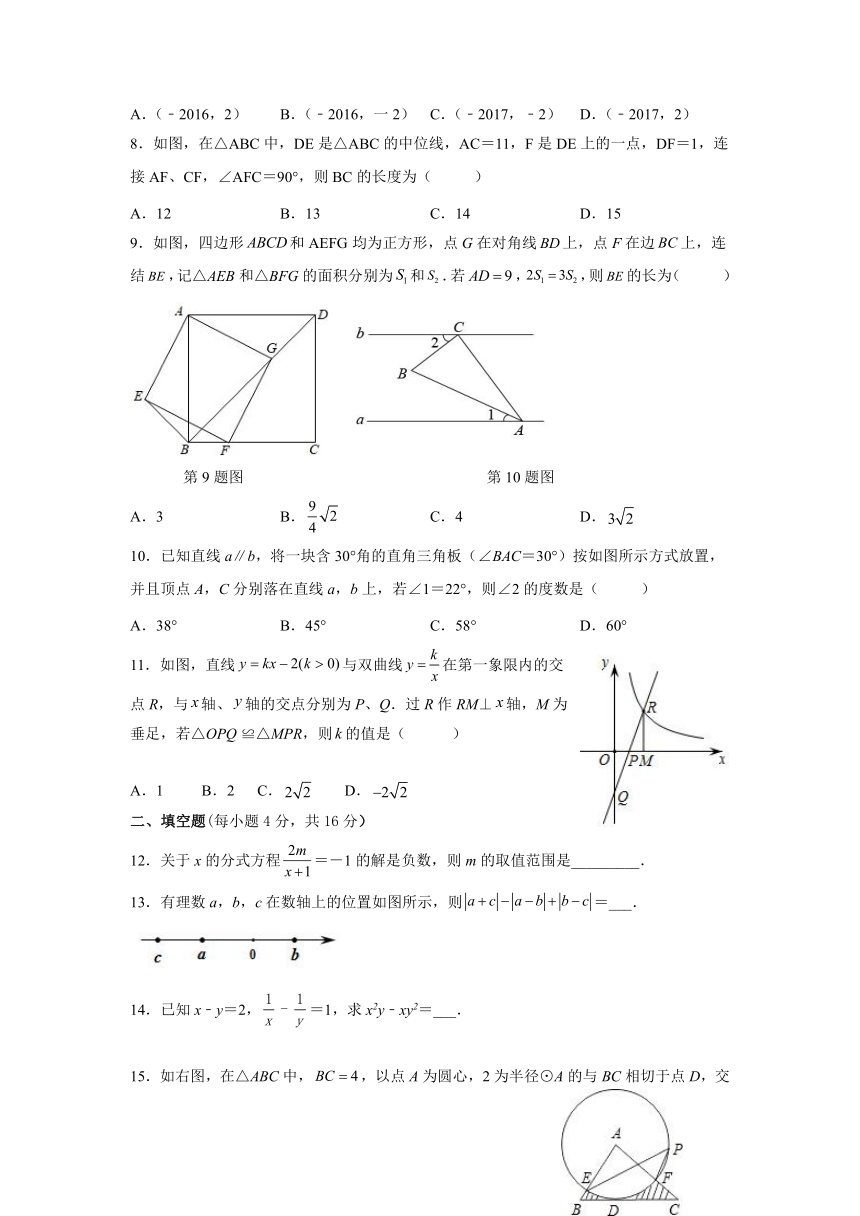
6.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=2,CD=1,则△ABC的边长为( )
第6题图 第8题图
A.3 B.4 C.5 D.6
7.已知M(2,2).规定“把点M先作关于x轴对称,再向左平移1个单位”为一次变换.那么连续经过2018次变换后,点M的坐标变为( )
A.(﹣2016,2) B.(﹣2016,一2) C.(﹣2017,﹣2) D.(﹣2017,2)
8.如图,在△ABC中,DE是△ABC的中位线,AC=11,F是DE上的一点,DF=1,连接AF、CF,∠AFC=90°,则BC的长度为( )
A.12 B.13 C.14 D.15
9.如图,四边形和AEFG均为正方形,点G在对角线上,点F在边上,连结,记△AEB和△BFG的面积分别为和.若,,则的长为( )
第9题图 第10题图
A.3 B. C.4 D.
10.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
11.如图,直线与双曲线在第一象限内的交点R,与轴、轴的交点分别为P、Q.过R作RM⊥轴,M为垂足,若△OPQ ≌△MPR,则的值是( )
A.1 B.2 C. D.
二、填空题(每小题4分,共16分)
12.关于x的分式方程=-1的解是负数,则m的取值范围是_________.
13.有理数a,b,c在数轴上的位置如图所示,则=___.
14.已知x﹣y=2,=1,求x2y﹣xy2=___.
15.如右图,在△ABC中,,以点A为圆心,2为半径⊙A的与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且,则图中阴影部分的面积是_______(结果保留).
三、解答题
16.计算:(每小题4分,共8分)
(1);
(2).
17.(8分)如图,等边△ABC的边长为10cm,点D在边AB上,且AD=4cm,点P在线段BC上,以每秒2cm的速度由点B向点C运动,同时点Q在线段CA上,由点C向点A运动.设点P运动时间为t秒,若某一时刻△BPD与△CQP全等,求此时t的值及点Q的运动速度.
18.(8分)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
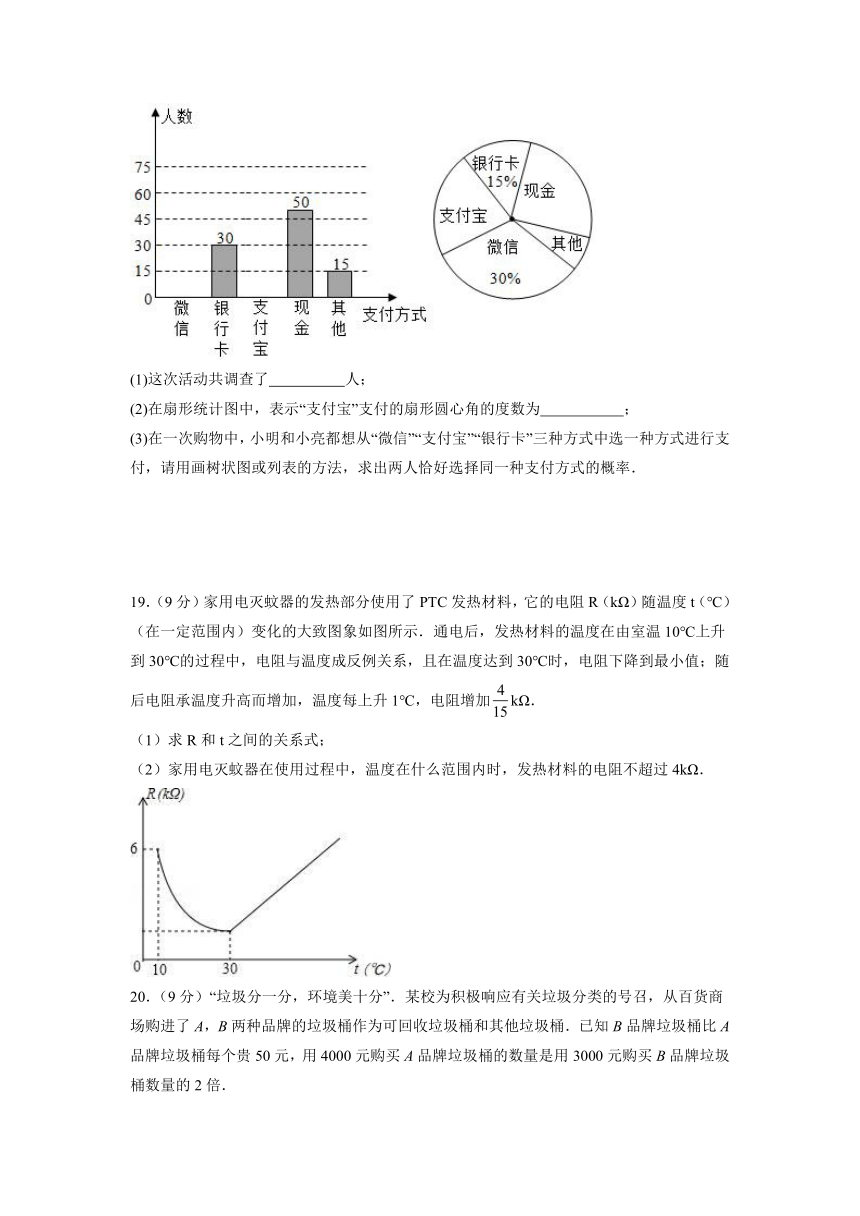
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
19.(9分)家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.
20.(9分)“垃圾分一分,环境美十分”.某校为积极响应有关垃圾分类的号召,从百货商场购进了A,B两种品牌的垃圾桶作为可回收垃圾桶和其他垃圾桶.已知B品牌垃圾桶比A品牌垃圾桶每个贵50元,用4000元购买A品牌垃圾桶的数量是用3000元购买B品牌垃圾桶数量的2倍.
(1)求购买一个A品牌、一个B品牌的垃圾桶各需多少元?
(2)若该中学决定再次准备用不超过6000元购进A,B两种品牌垃圾桶共50个,恰逢百货商场对两种品牌垃圾桶的售价进行调整:A品牌按第一次购买时售价的九折出售,B品牌比第一次购买时售价提高了20%,那么该学校此次最多可购买多少个B品牌垃圾桶?
21.(9分)如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,过点C作CG⊥AB交AB于点G,交AE于点F,过点E作EP⊥AB交AB于点P,∠EAD=∠DEB.
(1)求证:BC是⊙O的切线;
(2)连接FP,试猜想四边形CFPE的形状,并加以证明;
(3)若,AC=20,求四边形CFPE的面积.
衡山县第二中学2022-2023学年高一上学期8月入学考试
数学试卷
参考答案:
1.B 2.A 3.C 4.D 5.B 6.B
7.A 8.B 9.D 10.A 11.C
12. 且 13. 14. 15.2
16.(1);(2)2
解:(1)原式==;
(2)原式=..
17.当t=2s,点Q运动的速度为2cm/s;当t=2.5s,点Q运动的速度为2.4cm/s时,△BPD与△CQP全等.
解:由题意得:AD=4cm,BD=6cm,BP=2t,CP=10-2t,
∵△ABC为等边三角形,
∴∠B=∠C=60°,
当BP=CQ,BD=CP时,△BPD≌△CQP(SAS),
即CQ=2t,10-2t=6,解得t=2,
∴CQ=4,
∴点Q运动的速度为=2(cm/s);
当BP=CP,BD=CQ时,△BPD≌△CPQ(SAS),
即2t=10-2t,CQ=BD=6,解得t=2.5,
∴点Q运动的速度为=2.4(cm/s);
综上所述,当t=2s,点Q运动的速度为2cm/s;当t=2.5s,点Q运动的速度为2.4cm/s时,△BPD与△CQP全等.
18.【答案】(1)200
(2)81°
(3)
19.(1)见解析;(2)15℃~37.5℃
解:(1)∵温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,
∴当10≤t≤30时,设关系为R=,
将(10,6)代入上式中得:6=,解得k=60,
故当10≤t≤30时,R=;
将t=30℃代入上式中得:R==2,
∴温度在30℃时,电阻R=2(kΩ),
∵在温度达到30℃时,电阻下降到最小值,随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ,
∴当t≥30时,R=2+(t﹣30)=t﹣6,
故R和t之间的关系式为R= ;
(2)把R=4代入R=t﹣6,得t=37.5,
把R=4代入R=,得t=15,
所以,温度在15℃~37.5℃时,发热材料的电阻不超过4kΩ.
20.(1)购买一个A品牌垃圾桶需100元,购买一个B品牌垃圾桶需150元;(2)该学校此次最多可购买16个B品牌垃圾桶
解:(1)设购买一个A品牌垃圾桶需x元,则购买一个B品牌垃圾桶需(x+50)元,
依题意,得:,
解得:x=100,
经检验,x=100是原方程的解,且符合题意,
∴x+50=150.
答:购买一个A品牌垃圾桶需100元,购买一个B品牌垃圾桶需150元.
(2)设该学校此次购买m个B品牌垃圾桶,则购买(50﹣m)个A品牌垃圾桶,
依题意,得:100×0.9(50﹣m)+150×(1+20%)m≤6000,
解得:m≤.
因为m是正整数,所以m最大值是16.
答:该学校此次最多可购买16个B品牌垃圾桶.
21.(1)见解析;(2)四边形CFPE是菱形,理由见解析;(3)CFPE的面积=80
证明:(1)连接OE,
∵OE=OD,
∴∠OED=∠ADE,
∵AD是直径,
∴∠AED=90°,
∴∠EAD+∠ADE=90°,
∴∠EAD+∠OED=90°,
又∵∠DEB=∠EAD,
∴∠DEB+∠OED=90°,
∴∠BEO=90°,
∴OE⊥BC,
∴BC是⊙O的切线.
(2)连接FP,则四边形CFPE是菱形,理由如下:
∵∠BEO=∠ACB=90°,
∴AC∥OE,
∴∠CAE=∠OEA,
∵OA=OE,
∴∠EAO=∠AEO,
∴∠CAE=∠EAO,
又∵EP⊥AB,∠ACB=90°,
∴CE=EP;
∵∠CAE=∠EAP,
∴∠AEC=∠AFG=∠CFE,
∴CF=CE,
∴CF=PE,
∵CG⊥AB,EP⊥AB,
∴CF∥EP,
∴四边形CFPE是平行四边形,
又∵CF=PF,
∴四边形CFPE是菱形,
(3)∵sin∠ABC=sin∠ACG=,
∵AC=20,
∴AG=12,
∴CG=,
∵∠CAE=∠EAP,CE⊥AC,EP⊥AB,
∴CE=PE,
在Rt△CAE和Rt△OAE中,
,
∴Rt△ACE≌Rt△APE(HL),
∴AP=AC=20,
∴PG=AP-AG=20-12=8,
∵FP2=FG2+PG2,
∴FP2=(16-FP)2+82,
解得:FP=10,
∴CF=FP=10,
∴四边形CFPE的面积=CF GP=10×8=80.
数学试卷
第I卷(选择题)
一、单选题(每小题3分,共33分)
1.下列结论成立的是( ).
A.若,则 B.若,则
C.若,则 D.若,则
2.随着我国金融科技不断发展,网络消费、网上购物已成为人们生活不可或缺的一部分,今年“双十一”天猫成交额高达2684亿元.将数据“2684”用科学记数法表示( )
A. B. C. D.
3.下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. B. C. D.
4.是某三角形三边的长,则等于( )
A. B. C.10 D.4
5.已知点在第三象限,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
6.如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=2,CD=1,则△ABC的边长为( )
第6题图 第8题图
A.3 B.4 C.5 D.6
7.已知M(2,2).规定“把点M先作关于x轴对称,再向左平移1个单位”为一次变换.那么连续经过2018次变换后,点M的坐标变为( )
A.(﹣2016,2) B.(﹣2016,一2) C.(﹣2017,﹣2) D.(﹣2017,2)
8.如图,在△ABC中,DE是△ABC的中位线,AC=11,F是DE上的一点,DF=1,连接AF、CF,∠AFC=90°,则BC的长度为( )
A.12 B.13 C.14 D.15
9.如图,四边形和AEFG均为正方形,点G在对角线上,点F在边上,连结,记△AEB和△BFG的面积分别为和.若,,则的长为( )
第9题图 第10题图
A.3 B. C.4 D.
10.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
11.如图,直线与双曲线在第一象限内的交点R,与轴、轴的交点分别为P、Q.过R作RM⊥轴,M为垂足,若△OPQ ≌△MPR,则的值是( )
A.1 B.2 C. D.
二、填空题(每小题4分,共16分)
12.关于x的分式方程=-1的解是负数,则m的取值范围是_________.
13.有理数a,b,c在数轴上的位置如图所示,则=___.
14.已知x﹣y=2,=1,求x2y﹣xy2=___.
15.如右图,在△ABC中,,以点A为圆心,2为半径⊙A的与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且,则图中阴影部分的面积是_______(结果保留).
三、解答题
16.计算:(每小题4分,共8分)
(1);
(2).
17.(8分)如图,等边△ABC的边长为10cm,点D在边AB上,且AD=4cm,点P在线段BC上,以每秒2cm的速度由点B向点C运动,同时点Q在线段CA上,由点C向点A运动.设点P运动时间为t秒,若某一时刻△BPD与△CQP全等,求此时t的值及点Q的运动速度.
18.(8分)随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;
(2)在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(3)在一次购物中,小明和小亮都想从“微信”“支付宝”“银行卡”三种方式中选一种方式进行支付,请用画树状图或列表的方法,求出两人恰好选择同一种支付方式的概率.
19.(9分)家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.
20.(9分)“垃圾分一分,环境美十分”.某校为积极响应有关垃圾分类的号召,从百货商场购进了A,B两种品牌的垃圾桶作为可回收垃圾桶和其他垃圾桶.已知B品牌垃圾桶比A品牌垃圾桶每个贵50元,用4000元购买A品牌垃圾桶的数量是用3000元购买B品牌垃圾桶数量的2倍.
(1)求购买一个A品牌、一个B品牌的垃圾桶各需多少元?
(2)若该中学决定再次准备用不超过6000元购进A,B两种品牌垃圾桶共50个,恰逢百货商场对两种品牌垃圾桶的售价进行调整:A品牌按第一次购买时售价的九折出售,B品牌比第一次购买时售价提高了20%,那么该学校此次最多可购买多少个B品牌垃圾桶?
21.(9分)如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,过点C作CG⊥AB交AB于点G,交AE于点F,过点E作EP⊥AB交AB于点P,∠EAD=∠DEB.
(1)求证:BC是⊙O的切线;
(2)连接FP,试猜想四边形CFPE的形状,并加以证明;
(3)若,AC=20,求四边形CFPE的面积.
衡山县第二中学2022-2023学年高一上学期8月入学考试
数学试卷
参考答案:
1.B 2.A 3.C 4.D 5.B 6.B
7.A 8.B 9.D 10.A 11.C
12. 且 13. 14. 15.2
16.(1);(2)2
解:(1)原式==;
(2)原式=..
17.当t=2s,点Q运动的速度为2cm/s;当t=2.5s,点Q运动的速度为2.4cm/s时,△BPD与△CQP全等.
解:由题意得:AD=4cm,BD=6cm,BP=2t,CP=10-2t,
∵△ABC为等边三角形,
∴∠B=∠C=60°,
当BP=CQ,BD=CP时,△BPD≌△CQP(SAS),
即CQ=2t,10-2t=6,解得t=2,
∴CQ=4,
∴点Q运动的速度为=2(cm/s);
当BP=CP,BD=CQ时,△BPD≌△CPQ(SAS),
即2t=10-2t,CQ=BD=6,解得t=2.5,
∴点Q运动的速度为=2.4(cm/s);
综上所述,当t=2s,点Q运动的速度为2cm/s;当t=2.5s,点Q运动的速度为2.4cm/s时,△BPD与△CQP全等.
18.【答案】(1)200
(2)81°
(3)
19.(1)见解析;(2)15℃~37.5℃
解:(1)∵温度在由室温10℃上升到30℃的过程中,电阻与温度成反比例关系,
∴当10≤t≤30时,设关系为R=,
将(10,6)代入上式中得:6=,解得k=60,
故当10≤t≤30时,R=;
将t=30℃代入上式中得:R==2,
∴温度在30℃时,电阻R=2(kΩ),
∵在温度达到30℃时,电阻下降到最小值,随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ,
∴当t≥30时,R=2+(t﹣30)=t﹣6,
故R和t之间的关系式为R= ;
(2)把R=4代入R=t﹣6,得t=37.5,
把R=4代入R=,得t=15,
所以,温度在15℃~37.5℃时,发热材料的电阻不超过4kΩ.
20.(1)购买一个A品牌垃圾桶需100元,购买一个B品牌垃圾桶需150元;(2)该学校此次最多可购买16个B品牌垃圾桶
解:(1)设购买一个A品牌垃圾桶需x元,则购买一个B品牌垃圾桶需(x+50)元,
依题意,得:,
解得:x=100,
经检验,x=100是原方程的解,且符合题意,
∴x+50=150.
答:购买一个A品牌垃圾桶需100元,购买一个B品牌垃圾桶需150元.
(2)设该学校此次购买m个B品牌垃圾桶,则购买(50﹣m)个A品牌垃圾桶,
依题意,得:100×0.9(50﹣m)+150×(1+20%)m≤6000,
解得:m≤.
因为m是正整数,所以m最大值是16.
答:该学校此次最多可购买16个B品牌垃圾桶.
21.(1)见解析;(2)四边形CFPE是菱形,理由见解析;(3)CFPE的面积=80
证明:(1)连接OE,
∵OE=OD,
∴∠OED=∠ADE,
∵AD是直径,
∴∠AED=90°,
∴∠EAD+∠ADE=90°,
∴∠EAD+∠OED=90°,
又∵∠DEB=∠EAD,
∴∠DEB+∠OED=90°,
∴∠BEO=90°,
∴OE⊥BC,
∴BC是⊙O的切线.
(2)连接FP,则四边形CFPE是菱形,理由如下:
∵∠BEO=∠ACB=90°,
∴AC∥OE,
∴∠CAE=∠OEA,
∵OA=OE,
∴∠EAO=∠AEO,
∴∠CAE=∠EAO,
又∵EP⊥AB,∠ACB=90°,
∴CE=EP;
∵∠CAE=∠EAP,
∴∠AEC=∠AFG=∠CFE,
∴CF=CE,
∴CF=PE,
∵CG⊥AB,EP⊥AB,
∴CF∥EP,
∴四边形CFPE是平行四边形,
又∵CF=PF,
∴四边形CFPE是菱形,
(3)∵sin∠ABC=sin∠ACG=,
∵AC=20,
∴AG=12,
∴CG=,
∵∠CAE=∠EAP,CE⊥AC,EP⊥AB,
∴CE=PE,
在Rt△CAE和Rt△OAE中,
,
∴Rt△ACE≌Rt△APE(HL),
∴AP=AC=20,
∴PG=AP-AG=20-12=8,
∵FP2=FG2+PG2,
∴FP2=(16-FP)2+82,
解得:FP=10,
∴CF=FP=10,
∴四边形CFPE的面积=CF GP=10×8=80.
同课章节目录
