安徽省六校教育研究会2022-2023学年高一上学期8月入学考试数学试题(Word版含答案)
文档属性
| 名称 | 安徽省六校教育研究会2022-2023学年高一上学期8月入学考试数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 22:23:15 | ||
图片预览



文档简介
安徽六校教育研究会 2022 级高一新生入学素质测试
数学试题卷
考试范围: 初中; 满分 100 分, 考试时间: 120 分钟
第Ⅰ卷(选择题)
一、单选题 (共 10 小题, 每题 3 分)
1. PM2.5 是指大气中直径小于或等于 的颗粒物, 含有大量有毒、有害物质, 也 称可入肺颗粒物, 将 用科学记数法表示为( )
A.
B.
C.
D.
2. 如图是某几何体的展开图, 该几何体是( )
A. 长方体
B. 圆柱
C. 圆锥
D. 三棱柱
3. 某药店在今年 6 月份购进了一批口罩, 这批口罩包括一次性医用外科口罩和 口罩,且两种口罩的只数相同, 其中一次性医用外科口罩花费 1600 元, 口罩花费 9600 元. 已知一次性医用外科口罩的单价比 口罩的单价少 10 元, 那么一次性医用外科口罩的单价为多少元 设一次性医用外科口罩单价为 元, 则列方程正确的是( )
A.
B.
C.
D.
4. 在对一组样本数据进行分析时, 小凡列出了方差的计算公式:
, 根据公式不能得到的是( )
A. 众数是 6
B. 平均数是 8
C. 方差是 6
D. 中位数是 8
5. 如图, 在正方形方格纸中, 每个小正方形的边长都相等, 都在格点处, 与 相交于点 , 则 的值为( )
A.
B.
C.
D.
6.已知 1 和 3 是关于 的方程 的两个根, 且关于 的方程 有两个相等的实数根, 则实数 的值是( )
A. 1 或 B. 或 C. 或 D.1 或
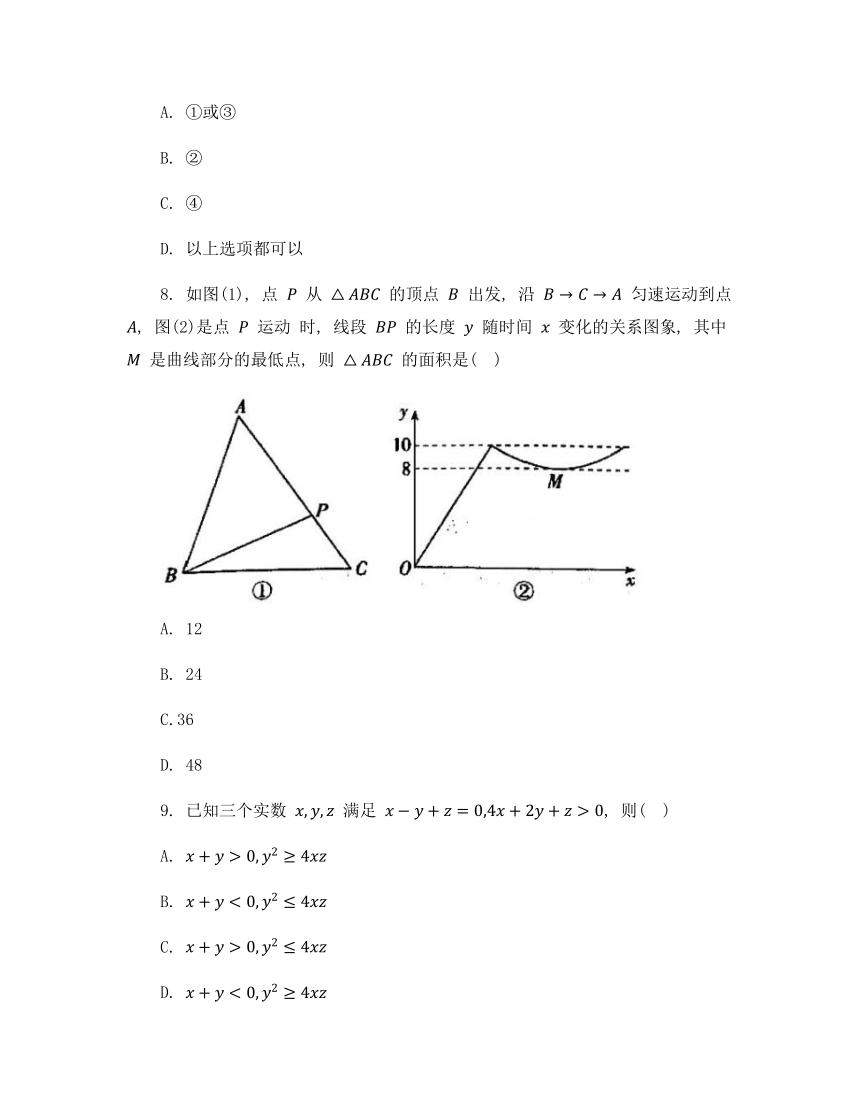
7.如图, 大矩形分割成五个小矩形, ④号、⑤号均为正方形, 其中⑤号正方形边长为 1 .若②号矩形的长与宽的差为 2 , 则知道哪个小矩形的周长, 就一定能算出这个大矩形的面积( )
A. ①或③
B. ②
C. ④
D. 以上选项都可以
8. 如图(1), 点 从 的顶点 出发, 沿 匀速运动到点 , 图(2)是点 运动 时, 线段 的长度 随时间 变化的关系图象, 其中 是曲线部分的最低点, 则 的面积是( )
A. 12
B. 24
C.36
D. 48
9. 已知三个实数 满足 , 则( )
A.
B.
C.
D.
10. 如图, 将一直角三角形纸片的直角边 折叠, 折痕为 与 上 重合, 裁去 ,已知 , 在 上任取一点 , 将 沿 翻折, 得到 ,与 重叠部分记为 . 当 为直角三角形时, 长可以为多少
① ; ② ; ③ ; ④ . 以上答案正确的有( )
A.①③ B.①② C.①②④ D.①②③
第Ⅱ卷(非选择题)
二、填空题(共 4 题, 每题 3 分)
11 因式分解: .
12. 阅读材料: 余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理, 运用它 可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题. 余弦定理是这样描述的: 在 中, 所对的边分别为 , 则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的 2 倍.
用公式可描述为:
现已知在 中, , 则 .
13. 如图, 用相同的圆点按照一定的规律拼出图形. 第一幅图 4 个圆点, 第二幅图 7 个圆点,第三幅图 10 个圆点, 第四幅图 13 个圆点……按照此规律, 第一百幅图中圆点的个数是 .
14.函数 的图象由抛物线的一部分和一条射线组成, 且与直线 为常数) 相交于三个不同的点 设 , 则 的取值范围是 .
三、解答题
15. (4 分) 计算: .
16. (4 分) 如图, 在平面直角坐标系中, 已知 三个顶点的坐标分别为 , B , C .
(1) 画出将 向左平移 5 个单位得到的 ;
(2) 画出将 绕原点 顺时针旋转 得到的 .
17. (5 分) 观察下列关于自然数的等式:
(1)
(2)
(3) ③
……
根据上述规律解决下列问题:
(1) 写出第 4 个等式: ;
(2) 写出你猜想的第 个等式 (用含 的式子表示), 并证明其正确性.
18. (6 分) 为了让乘客有良好的候车环境, 某市在公交站牌旁投放大量的候车亭 (如图(1), 其结构示意图的侧面如图(2)所示, 其中支柱 的长为 , 且支柱 垂直于地面 , 顶棚横梁 长为 为镶接柱, 镶接柱与支柱的夹角 , 与顶棚横梁的 夹角 , 要求横梁一端点 在支柱 的延长线上, 此时测量得镶接点 与点 的距离为 . 根据以上测量数据, 求点 到地面 的距离. (结果精确到 , 参考 数据: .
19. (6 分)某工厂为贯彻落实“绿水青山就是金山银山“的发展理念, 投资组建了日废水处理量为 吨的废水处理车间, 对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大, 该车间经常无法完成当天工业废水的处理任务, 需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水, 每天需固定成本 30 元, 并且每处理一吨废水还需其他费用 8 元; 将废水交给第三方企业处理,每吨需支付 12 元. 根据记录,5 月 21 日,该厂产生工业废水 35 吨, 共花费废水处理费 370 元.
(1) 求该车间的日废水处理量 ;
(2) 为实现可持续发展, 走绿色发展之路, 工厂合理控制了生产规模, 使得每天废水处理 的平均费用不超过 10 元 / 吨, 试计算该厂一天产生的工业废水量的范围.
20. (7 分) 如图, 在 中, , 以 为直径作 交 于点 . 过点 作 , 垂足为 , 且交 的延长线于点 .
(1) 求证: 是 的切线;
(2) 已知 . 求 的长.
21. (8 分) 某校为了解学生每月零用钱情况, 从七、八、九年级 1200 名学生中随机抽取部分学生, 对他们今年 4 月份的零用钱支出情况进行调查统计并绘制成如下统计图 请根据图表中所给的信息, 解答下列问题:
(1)在这次调查中共随机抽取了 名学生, 图表中的 ;
(2)请估计该校今年 4 月份零用钱支出在 “范围的学生人数;
(3)在抽样的“节俭型”学生中, 有 2 位男生和 4 位女生, 校团委计划从中随机抽取两人参与“映山红”的公益活动, 求恰好抽中一男一女的概率.
22. (8 分) 如图, 抛物线 与直线 交于 两点, 交 轴于 两点, 连接 , 已知 .
(1) 求抛物线对应函数的解析式和 的值;
(2) 设 为线段 上一点 (不含端点), 连接 , 一动点 从点 出发, 沿线段 以每秒一个单位速度运动到 点, 再沿线段 以每秒 个单位的速度运动到 后停止, 当点 的坐标是多少时, 点 在整个运动中用时最少
23. (10 分) (1) 如图 1, 在 和 中, , , 连接 交于点 .
① 的值为 .
② 的度数为 .
(2) 如图 2, 在 和 中, , 连接 交 的延长线于点 . 计算 的值及 的度数;
(3) 在 (2) 的条件下, 将 绕点 在平面内旋转, 所在直线交于点 , 若 , 求当点 与点 重合时 的长.
数学试题卷
考试范围: 初中; 满分 100 分, 考试时间: 120 分钟
第Ⅰ卷(选择题)
一、单选题 (共 10 小题, 每题 3 分)
1. PM2.5 是指大气中直径小于或等于 的颗粒物, 含有大量有毒、有害物质, 也 称可入肺颗粒物, 将 用科学记数法表示为( )
A.
B.
C.
D.
2. 如图是某几何体的展开图, 该几何体是( )
A. 长方体
B. 圆柱
C. 圆锥
D. 三棱柱
3. 某药店在今年 6 月份购进了一批口罩, 这批口罩包括一次性医用外科口罩和 口罩,且两种口罩的只数相同, 其中一次性医用外科口罩花费 1600 元, 口罩花费 9600 元. 已知一次性医用外科口罩的单价比 口罩的单价少 10 元, 那么一次性医用外科口罩的单价为多少元 设一次性医用外科口罩单价为 元, 则列方程正确的是( )
A.
B.
C.
D.
4. 在对一组样本数据进行分析时, 小凡列出了方差的计算公式:
, 根据公式不能得到的是( )
A. 众数是 6
B. 平均数是 8
C. 方差是 6
D. 中位数是 8
5. 如图, 在正方形方格纸中, 每个小正方形的边长都相等, 都在格点处, 与 相交于点 , 则 的值为( )
A.
B.
C.
D.
6.已知 1 和 3 是关于 的方程 的两个根, 且关于 的方程 有两个相等的实数根, 则实数 的值是( )
A. 1 或 B. 或 C. 或 D.1 或
7.如图, 大矩形分割成五个小矩形, ④号、⑤号均为正方形, 其中⑤号正方形边长为 1 .若②号矩形的长与宽的差为 2 , 则知道哪个小矩形的周长, 就一定能算出这个大矩形的面积( )
A. ①或③
B. ②
C. ④
D. 以上选项都可以
8. 如图(1), 点 从 的顶点 出发, 沿 匀速运动到点 , 图(2)是点 运动 时, 线段 的长度 随时间 变化的关系图象, 其中 是曲线部分的最低点, 则 的面积是( )
A. 12
B. 24
C.36
D. 48
9. 已知三个实数 满足 , 则( )
A.
B.
C.
D.
10. 如图, 将一直角三角形纸片的直角边 折叠, 折痕为 与 上 重合, 裁去 ,已知 , 在 上任取一点 , 将 沿 翻折, 得到 ,与 重叠部分记为 . 当 为直角三角形时, 长可以为多少
① ; ② ; ③ ; ④ . 以上答案正确的有( )
A.①③ B.①② C.①②④ D.①②③
第Ⅱ卷(非选择题)
二、填空题(共 4 题, 每题 3 分)
11 因式分解: .
12. 阅读材料: 余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理, 运用它 可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题. 余弦定理是这样描述的: 在 中, 所对的边分别为 , 则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的 2 倍.
用公式可描述为:
现已知在 中, , 则 .
13. 如图, 用相同的圆点按照一定的规律拼出图形. 第一幅图 4 个圆点, 第二幅图 7 个圆点,第三幅图 10 个圆点, 第四幅图 13 个圆点……按照此规律, 第一百幅图中圆点的个数是 .
14.函数 的图象由抛物线的一部分和一条射线组成, 且与直线 为常数) 相交于三个不同的点 设 , 则 的取值范围是 .
三、解答题
15. (4 分) 计算: .
16. (4 分) 如图, 在平面直角坐标系中, 已知 三个顶点的坐标分别为 , B , C .
(1) 画出将 向左平移 5 个单位得到的 ;
(2) 画出将 绕原点 顺时针旋转 得到的 .
17. (5 分) 观察下列关于自然数的等式:
(1)
(2)
(3) ③
……
根据上述规律解决下列问题:
(1) 写出第 4 个等式: ;
(2) 写出你猜想的第 个等式 (用含 的式子表示), 并证明其正确性.
18. (6 分) 为了让乘客有良好的候车环境, 某市在公交站牌旁投放大量的候车亭 (如图(1), 其结构示意图的侧面如图(2)所示, 其中支柱 的长为 , 且支柱 垂直于地面 , 顶棚横梁 长为 为镶接柱, 镶接柱与支柱的夹角 , 与顶棚横梁的 夹角 , 要求横梁一端点 在支柱 的延长线上, 此时测量得镶接点 与点 的距离为 . 根据以上测量数据, 求点 到地面 的距离. (结果精确到 , 参考 数据: .
19. (6 分)某工厂为贯彻落实“绿水青山就是金山银山“的发展理念, 投资组建了日废水处理量为 吨的废水处理车间, 对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大, 该车间经常无法完成当天工业废水的处理任务, 需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水, 每天需固定成本 30 元, 并且每处理一吨废水还需其他费用 8 元; 将废水交给第三方企业处理,每吨需支付 12 元. 根据记录,5 月 21 日,该厂产生工业废水 35 吨, 共花费废水处理费 370 元.
(1) 求该车间的日废水处理量 ;
(2) 为实现可持续发展, 走绿色发展之路, 工厂合理控制了生产规模, 使得每天废水处理 的平均费用不超过 10 元 / 吨, 试计算该厂一天产生的工业废水量的范围.
20. (7 分) 如图, 在 中, , 以 为直径作 交 于点 . 过点 作 , 垂足为 , 且交 的延长线于点 .
(1) 求证: 是 的切线;
(2) 已知 . 求 的长.
21. (8 分) 某校为了解学生每月零用钱情况, 从七、八、九年级 1200 名学生中随机抽取部分学生, 对他们今年 4 月份的零用钱支出情况进行调查统计并绘制成如下统计图 请根据图表中所给的信息, 解答下列问题:
(1)在这次调查中共随机抽取了 名学生, 图表中的 ;
(2)请估计该校今年 4 月份零用钱支出在 “范围的学生人数;
(3)在抽样的“节俭型”学生中, 有 2 位男生和 4 位女生, 校团委计划从中随机抽取两人参与“映山红”的公益活动, 求恰好抽中一男一女的概率.
22. (8 分) 如图, 抛物线 与直线 交于 两点, 交 轴于 两点, 连接 , 已知 .
(1) 求抛物线对应函数的解析式和 的值;
(2) 设 为线段 上一点 (不含端点), 连接 , 一动点 从点 出发, 沿线段 以每秒一个单位速度运动到 点, 再沿线段 以每秒 个单位的速度运动到 后停止, 当点 的坐标是多少时, 点 在整个运动中用时最少
23. (10 分) (1) 如图 1, 在 和 中, , , 连接 交于点 .
① 的值为 .
② 的度数为 .
(2) 如图 2, 在 和 中, , 连接 交 的延长线于点 . 计算 的值及 的度数;
(3) 在 (2) 的条件下, 将 绕点 在平面内旋转, 所在直线交于点 , 若 , 求当点 与点 重合时 的长.
同课章节目录
