九年级数学苏科版上册 2.1圆 课时练(word版 含答案)
文档属性
| 名称 | 九年级数学苏科版上册 2.1圆 课时练(word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 11:17:36 | ||
图片预览

文档简介
课 时 练
2.1 圆
一、选择题(本大题共6小题,共18分)
下列条件中,能确定一个圆的是( )
A. 以点为圆心 B. 以长为半径
C. 以点为圆心,长为半径 D. 经过已知点
O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与O的位置关系为( )
A. 点在上 B. 点在内 C. 点在外 D. 无法确定
在平面直角坐标系中,O的直径为26,圆心O为坐标原点,则点P(-12,-5)与O的位置关系是( )
A. 点在上 B. 点在外 C. 点在内 D. 无法确定
有下列说法:直径是弦;弧是半圆;经过圆内一点可以作无数条直径;圆心相同的两个圆是同心圆.其中,不正确的个数是( )
A. B. C. D.
下列说法中,正确的是( )
A. 弦是直径 B. 长度相等的弧是等弧
C. 半圆是弧 D. 过圆心的线段是直径
如图,点A、B、C在O上,ACOB,BAO=,则BOC的度数为( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
大、小两个圆的半径分别是5厘米和3厘米,大小两个圆的周长的比是(),面积的比是()。
与点A的距离为3cm的点所组成的平面图形是 .
已知正方形ABCD的边长为2cm,以点A为圆心,2cm为半径作A,则点B在A ,点C在A ,点D在A .
在RtABC中,C=,AC=3cm,BC=4cm,D是AB的中点,以点C为圆心,3cm为半径作圆,则A、B、C、D四个点中,在C内的点有 个.
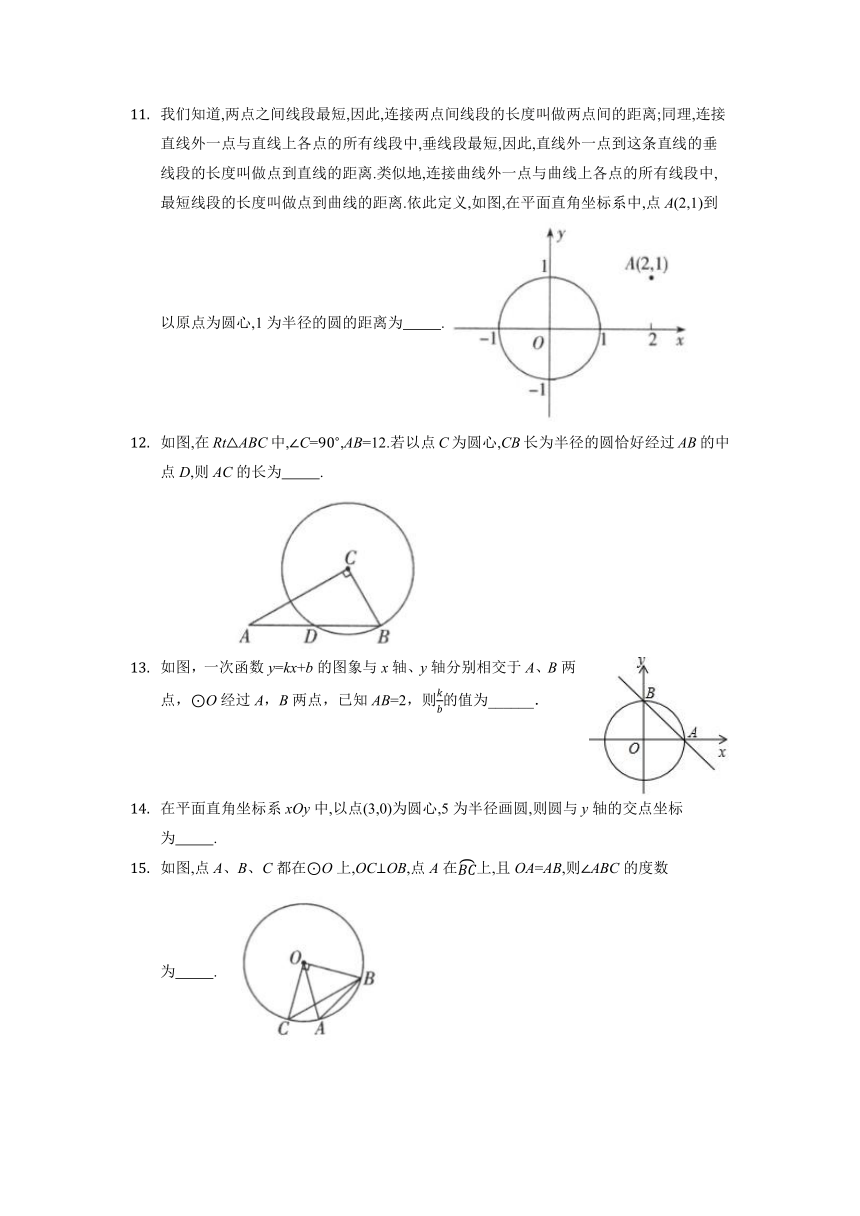
我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点A(2,1)到以原点为圆心,1为半径的圆的距离为 .
如图,在RtABC中,C=,AB=12.若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AC的长为 .
如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A、B两点,⊙O经过A,B两点,已知AB=2,则的值为______.
在平面直角坐标系xOy中,以点(3,0)为圆心,5为半径画圆,则圆与y轴的交点坐标为 .
如图,点A、B、C都在O上,OCOB,点A在上,且OA=AB,则ABC的度数为 .
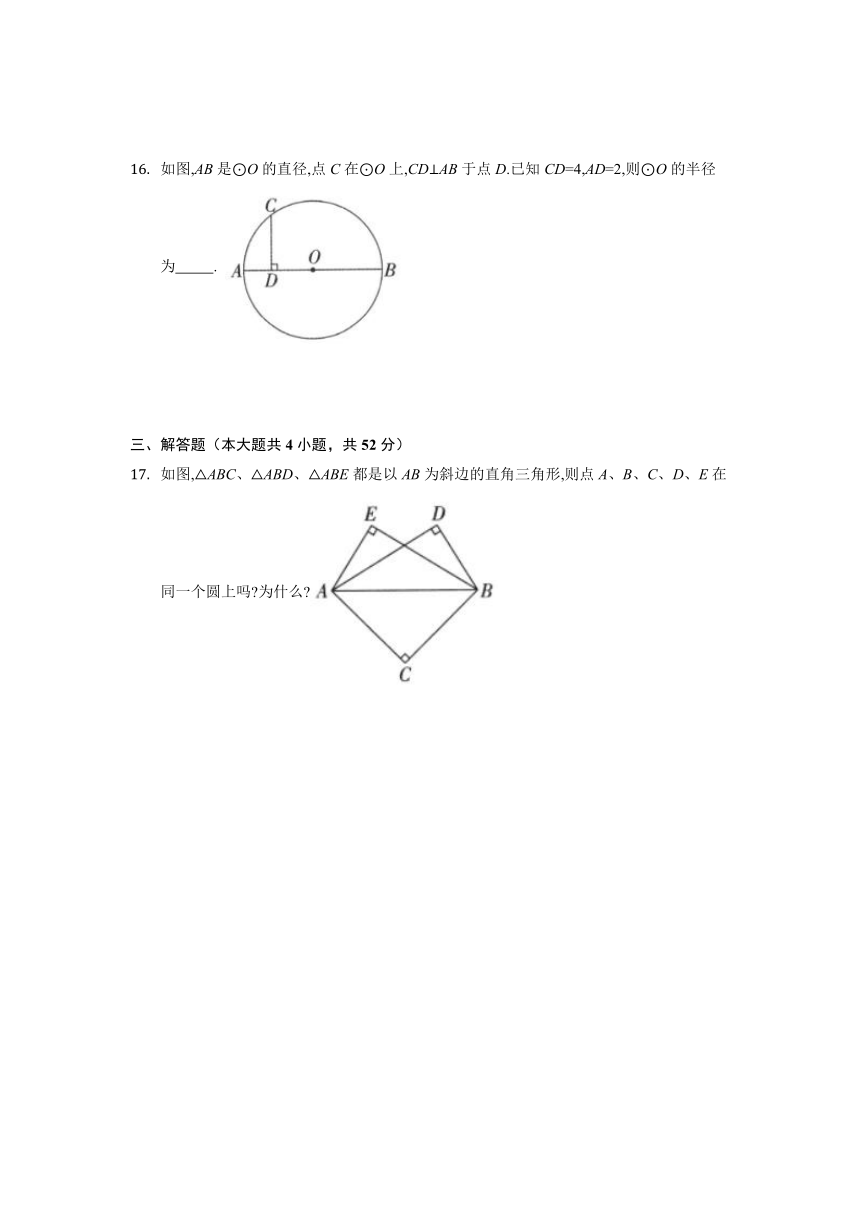
如图,AB是O的直径,点C在O上,CDAB于点D.已知CD=4,AD=2,则O的半径为 .
三、解答题(本大题共4小题,共52分)
如图,ABC、ABD、ABE都是以AB为斜边的直角三角形,则点A、B、C、D、E在同一个圆上吗 为什么
如图,在平面直角坐标系中,已知A(8,0)、B(0,6)、C(1,7),M经过原点O及点A、B,AB为M的直径.
(1)求M的半径及圆心M的坐标;
(2)判断点C与M的位置关系,并说明理由.
如图,A、B、C是O上的三点,BO平分ABC.弦BA与弦BC相等吗 为什么
如图,AB、CD是O的两条弦.若AOB+C=,COD=A,求AOB的度数.
参考答案
1.C
2.B
3.A
4.C
5.C
6.B
7.5:3;25:9
8.以点A为圆心,3cm长为半径的圆
9.上 外 上
10.2
11.-1
12.6
13.-
14.(0,4)、(0,-4)
15.
16.5
17.解:点A、B、C、D、E在同一个圆上
取AB的中点O,连接EO、CO、DO.
ABC、ABD、ABE都是以AB为斜边的直角三角形,
OC=AB,OD=AB,OE=AB.
OA=OB=OC=OD=OE=AB.
点A、B、C、D、E都在以点O为圆心,AB长为半径的圆上
18.解:(1)作MNOA交x轴于N.
AOB=,
AB是M的直径,
MN为AOB的中位线.
A(8,0)、B(0,6),
M(4,3),AB==10,
M的半径为5.
(2)点C在M上.
理由:C(1,7)、M(4,3),
CM==5,
点C在M上.
19.解:弦BA与弦BC相等.
如图,连接OA、OC.
OA=OB,OB=OC,
ABO=BAO,CBO=BCO.
BO平分ABC,
ABO=CBO.
BAO=BCO.
又BO=BO,
OABOCB.
BA=BC,即弦BA与弦BC相等.
20.解:设COD=A=x.
OA=OB,
A=B=x.
在OAB中,AOB=-2x.
又OC=OD,
C=D.
在COD中,C=(-x).
AOB+C=,
-2x+(-x)=,
解得x=,
AOB=-2x=-2=.
2.1 圆
一、选择题(本大题共6小题,共18分)
下列条件中,能确定一个圆的是( )
A. 以点为圆心 B. 以长为半径
C. 以点为圆心,长为半径 D. 经过已知点
O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与O的位置关系为( )
A. 点在上 B. 点在内 C. 点在外 D. 无法确定
在平面直角坐标系中,O的直径为26,圆心O为坐标原点,则点P(-12,-5)与O的位置关系是( )
A. 点在上 B. 点在外 C. 点在内 D. 无法确定
有下列说法:直径是弦;弧是半圆;经过圆内一点可以作无数条直径;圆心相同的两个圆是同心圆.其中,不正确的个数是( )
A. B. C. D.
下列说法中,正确的是( )
A. 弦是直径 B. 长度相等的弧是等弧
C. 半圆是弧 D. 过圆心的线段是直径
如图,点A、B、C在O上,ACOB,BAO=,则BOC的度数为( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
大、小两个圆的半径分别是5厘米和3厘米,大小两个圆的周长的比是(),面积的比是()。
与点A的距离为3cm的点所组成的平面图形是 .
已知正方形ABCD的边长为2cm,以点A为圆心,2cm为半径作A,则点B在A ,点C在A ,点D在A .
在RtABC中,C=,AC=3cm,BC=4cm,D是AB的中点,以点C为圆心,3cm为半径作圆,则A、B、C、D四个点中,在C内的点有 个.
我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点A(2,1)到以原点为圆心,1为半径的圆的距离为 .
如图,在RtABC中,C=,AB=12.若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,则AC的长为 .
如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A、B两点,⊙O经过A,B两点,已知AB=2,则的值为______.
在平面直角坐标系xOy中,以点(3,0)为圆心,5为半径画圆,则圆与y轴的交点坐标为 .
如图,点A、B、C都在O上,OCOB,点A在上,且OA=AB,则ABC的度数为 .
如图,AB是O的直径,点C在O上,CDAB于点D.已知CD=4,AD=2,则O的半径为 .
三、解答题(本大题共4小题,共52分)
如图,ABC、ABD、ABE都是以AB为斜边的直角三角形,则点A、B、C、D、E在同一个圆上吗 为什么
如图,在平面直角坐标系中,已知A(8,0)、B(0,6)、C(1,7),M经过原点O及点A、B,AB为M的直径.
(1)求M的半径及圆心M的坐标;
(2)判断点C与M的位置关系,并说明理由.
如图,A、B、C是O上的三点,BO平分ABC.弦BA与弦BC相等吗 为什么
如图,AB、CD是O的两条弦.若AOB+C=,COD=A,求AOB的度数.
参考答案
1.C
2.B
3.A
4.C
5.C
6.B
7.5:3;25:9
8.以点A为圆心,3cm长为半径的圆
9.上 外 上
10.2
11.-1
12.6
13.-
14.(0,4)、(0,-4)
15.
16.5
17.解:点A、B、C、D、E在同一个圆上
取AB的中点O,连接EO、CO、DO.
ABC、ABD、ABE都是以AB为斜边的直角三角形,
OC=AB,OD=AB,OE=AB.
OA=OB=OC=OD=OE=AB.
点A、B、C、D、E都在以点O为圆心,AB长为半径的圆上
18.解:(1)作MNOA交x轴于N.
AOB=,
AB是M的直径,
MN为AOB的中位线.
A(8,0)、B(0,6),
M(4,3),AB==10,
M的半径为5.
(2)点C在M上.
理由:C(1,7)、M(4,3),
CM==5,
点C在M上.
19.解:弦BA与弦BC相等.
如图,连接OA、OC.
OA=OB,OB=OC,
ABO=BAO,CBO=BCO.
BO平分ABC,
ABO=CBO.
BAO=BCO.
又BO=BO,
OABOCB.
BA=BC,即弦BA与弦BC相等.
20.解:设COD=A=x.
OA=OB,
A=B=x.
在OAB中,AOB=-2x.
又OC=OD,
C=D.
在COD中,C=(-x).
AOB+C=,
-2x+(-x)=,
解得x=,
AOB=-2x=-2=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
